Diatomic molecules and molecular ions in intense laser fields continue to attract the attention of the atomic and molecular physics community despite several years of study. One of the main goals in this research direction is to find a way to selectively break and form molecular bonds in photochemical reactions.^[1] With the advent of new laser technologies, in particular the carrier envelope phase (CEP) stabilized few-cycle pulses and the isolated subfemtosecond pulses, several control strategies have been proposed, taking advantage of controlling the motion of the electron wave packet in atoms and molecules.^{[2– 9]} The hydrogen molecular ion is of special interest since it is the simplest molecule, consisting of three particles only. It plays an important role in the theoretical and experimental studies of electron localization in the dissociation of molecules. In the previous work, ^{[10– 12]} coherent control with a two-color laser field to investigate the asymmetry dissociation of HD⁺ and was reported. Then the shaped laser pulse was proposed to control the dissociation pathway of . Compared with a single pulse, two sequential pulses were proven to locate more electrons on the selected pathway.^{[13– 16]} The combination of an ultraviolet (UV) pulse and a time-delayed near-infrared pulse was used to realize an electron localization probability as high as 85% on one of the two nuclei.^[13] More recently, a similar electron localization probability was obtained by using two-color mid- and near-infrared laser pulses.^[16]

In our previous work, ^{[17, 18]} a time-delayed terahertz (THz) pulse was utilized to steer the electron motion of between the two protons after an ultrashort UV laser pulse was used to excite the electron wave packet onto the dissociative 2pσ _u state.^{[19– 24]} Both the THz and the UV pulses were linearly polarized. By adjusting the time delay of the two pulses and the peak intensity of the THz pulse, an unprecedentedly high control ratio (the probability to localize electrons on one of the two nuclei) of 99.3% could be obtained, with almost zero ionization and 6.14% dissociation probability. The electron localization ratio could still be 96.3% even when the total dissociation probability reached 25.6%. For the dissociation of a diatomic molecule, a bound electron is driven back and forth between the potential of the dissociating molecule until the point where it can no longer overcome the barrier between the two nuclei, which is dependent on the distance between the two nuclei.^[13] The efficient dissociation control is only possible within a brief period of time, which is called the effective time for electron localization, and the final state is sensitive to the direction and the field intensity of the electric field of the control pulse.^{[17, 25]} In this paper, we investigate the dissociation control of and its isotopes with the combination of UV and THz pulses in Sections 2 and 3. In Section 4, the relationship between the effective time of the electron localization and the nuclear mass of the molecule is discussed.

We use a reduced-dimensional model for the molecular ion and its isotopes in the calculation. The molecular axis is assumed to be parallel to the polarization direction of the two linearly polarized laser fields. Then we can use the one-dimensional (1D) non-Born– Oppenheimer time-dependent Schrö dinger equation (TDSE) for the simulation.^[26] The corresponding TDSE can be written as (e = ħ = m_e = 1 in atomic units (a.u.), which are used throughout the paper unless otherwise stated)^{[17, 27– 30]}

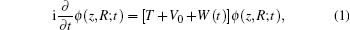where T is the free Hamiltonian of the system, V₀ stands for the Coulomb interactions, and W(t) describes the interaction with the external laser field. For our model, the kinetic energy T reads

and the Coulomb potential is

where R is the relative internuclear distance, z is the electronic coordinate with respect to the center of mass of the two nuclei, and μ = (1/m_p+ 1/m_n)^{− 1} and μ _e = (m_p+ m_n)/(m_p+ m_n+ 1) are the reduced masses, with m_e, m_p, and m_n being the masses of the electron, the proton, and the second nucleus (m_e = 1; m_p = 1837; m_n = 1837, 3674, 5511 for , HD⁺ , HT⁺ , respectively).

The interaction with the laser field is written in the dipole approximation (in the length gauge) as

The UV pulse is defined as E₂ (t) = E₂₀ sin (π t/T₂)²sin (ω ₂t), where T₂ is the total length of the pulse, i.e., 7.9 fs. The THz pulse is defined with the vector potential A(t) = − E₁₀/ω ₁ sin (π t/T₁)²cos (ω ₁t), where T₁ is the total length of the THz pulse; then E₁ (t) = − ∂ A(t)/∂ t. The total simulation time is defined by t_end, and Δ t is the time delay between the two pulses, which is defined as the difference between the envelope peaks of the two electric fields. When the envelope peak of the THz pulse is ahead, Δ t is positive, otherwise, Δ t is negative. The two channels of the dissociation of these three molecule ions are defined as^{[9, 13, 16, 31]}

where R_max corresponds to the boundary of the R axis, and φ (z, R; t_end) is the final wave function of our system. In the simulation, t_end = 106.8 fs when P_± , the probabilities of the electron localized on one of the protons (left − or right + ), are stable. The electron localization starts from about R = 5.7 a.u. So, we use R₀ = 5.7 a.u. in the definition of P_± .^[17]

In this simulation, the linearly polarized 228-nm UV pulse with an intensity of 5.0× 10¹⁴ W/cm² and a pulse length T₂ of 7.9 fs is used to resonantly excite the electron wave packet onto the dissociative state 2pσ _u. Then the 25.6-μ m (11.7 THz in frequency) THz pulse with an intensity of 3.8× 10¹² W/cm² and a pulse length T₁ of 85.3 fs is used to steer the electron motion.^[32] This THz pulse does not induce any further ionization. In the calculation, we set the dissociation asymmetry parameter as A = (P₊ − P₋ )/(P₊ + P₋ ).

To reveal the details of the electron localization control of , we define the time-dependent electron probabilities of different parts: PD_± for the electrons localized on the right (or left) proton, PG for the electrons of the high vibrational bound states, PGI_± and PI_± for the ionized electrons of the six sections, respectively. They are given by

In the definition of PD_± , we also choose R = 5.7 a.u., as depicted in Fig. 1(a). Figure 1(b) shows the temporal evolution probabilities of different parts of with the UV and THz pulses. The delay time between these two pulses is Δ t = − 9.4 fs. One can find that for , the effective time for electron localization lasts about 16.0 fs. For HD⁺ and HT⁺ , when the same way is applied, the effective time can also be obtained only with the time windows changed to 16.2 fs and 16.3 fs, respectively.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Time-dependent electron probabilities of different parts of . (b) Time-dependent electron probabilities of : PD± (t), PI± (t), PG(t), and PGI± (t), with UV and THz pulses at λ 2 = 228 nm, τ 2 = 7.9 fs, I2 = 5.0× 1014 W/cm2 and λ 1 = 25.6 μ m, τ 1 = 85.3 fs, I1 = 3.8× 1012 W/cm2, Δ respectively, and Δ t = − 9.4 fs.

In Fig. 2, we present the probabilities of electrons localized at the right (proton side, cycles) and the left (second nucleus side, stars) z axis, for the interaction of , HD⁺ , and HT⁺ with a single ultrashort UV pulse (the gray) or with a two-pulse scheme of the UV and THz spectral regimes with delay Δ t = 14.6 fs (the red). When only the UV pulse is on, for , are the electron localization probabilities of the two protons the same. While for the hetero-nuclear molecules, with the increase of the quality of the second nucleus, more electrons gather along the proton side for the unsymmetirc ground state distribution. When with the two-pulse regime, the dissociation asymmetry parameter A varies as a function of Δ t. In the simulation, one can find that for , HD⁺ , and HT⁺ , the variations of A are almost the same. When Δ t = 14.6 fs, A reaches the maximum, as shown in Fig. 3(a). For , when Δ t = 14.6 fs, P₊ = 0.235 and P₋ = 0.0097, 96.0% of all the dissociation electrons can be controlled to the right potential well. For HD⁺ and HT⁺ , when Δ t = 14.6 fs, P₊ = 0.199, 0.171 and P₋ = 0.0083, 0.0071, respectively. The localization ratios of the right nuclei are 96.08% and 96.0%, respectively, as shown in Fig. 2.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Dissociation probabilities with electron localization along the right (proton side, cycles) and the left (second nucleus side, stars) z axis for the interaction of , HD+ , and HT+ with an ultrashort UV pulse at λ 2 = 228 nm, τ 2 = 7.9 fs, and I2 = 5.0× 1014 W/cm2 (the gray) or with the UV pulse and a THz pulse at λ 1 = 25.6 μ m, τ 1 = 85.3 fs, I1 = 3.8× 1012 W/cm2, and Δ t = 14.6 fs (the red).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Asymmetry parameter A and ionization probability I as functions of Δ t with I1 = 3.8× 1012 W/cm2 and I2 = 5.0× 1014 W/cm2 for , HD+ , and HT+ . (b) The A and I as functions of the electric field strength of the UV pulse E20 with I1 = 3.8× 1012 W/cm2 and Δ t = 14.6 fs for , HD+ , and HT+ .

Figure 3(b) depicts the dissociation asymmetry parameter A and the ionization probability I of , HD⁺ , and HT⁺ as functions of the UV pulse field strength E₂₀ at Δ t = 14.6 fs and I₁ = 3.8× 10¹² W/cm². When E₂₀ is small, all the electrons of the dissociative states are excited onto the 2pσ _u state and a large localization ratio can be obtained with almost zero ionization and a small dissociation probability. For , when E₂₀ = 0.0446 a.u., A = 0.986, the electron localization ratio can reach 99.3% and the dissociation probability is 6.14%, with almost no ionization (less than 0.0013%). For HD⁺ and HT⁺ , when E₂₀ = 0.0446 a.u., the total dissociation probabilities and the electron localization ratios are 5.91%, 6.04% and 99.2%, 99.0%, respectively. The ionization ratio is also close to zero. With the increase of E₂₀, some electrons are excited onto the higher 3sσ state through the 3-photon resonance, which dramatically damages the electron localization control.^[18]

But why is the THz pulse useful? As shown in Refs. [17] and [18], the electron localization by using two laser pulses of UV and THz spectral regimes can be much higher than that in the previous work^[13] because there is an effective time for controlling the molecular dissociation. The half period of the control electric field needs to match the effective time of the molecule dissociation if a high control ratio is achieved. For , this effective time is about 16.0 fs, and when all the electrons of the dissociative states are excited onto the 2pσ _u state, the dissociation control is implemented more easily. With the coupled equations, the same result can be obtained as with the TDSE^[18]. So below, we use the coupled equations to investigate the effective time of homo-nuclear molecules with different masses. The coupled equations can be written as^{[17, 18, 33]}

where V_g (R) and V_u (R) are the binding and the dissociative potentials, respectively. and are the nuclear wave packets of the left and the right protons, respectively, ψ _g (R, t) and ψ _u (R, t) are the nuclear wave packets of states 1sσ _g and 2pσ _u, respectively, and V_gu (R, t) denotes the interaction with the external laser field. In Fig. 4(a), one can find the same effective time for effectively controlling the dissociation of as in Fig. 1(b). In this simulation, a Gaussian-type wave packet is pre-excited onto the dissociative state ψ _u with center position R = 3.3 a.u. (resonant with the 228-nm pulse). The effective time increases with the increasing nuclear mass of the homo-nuclear molecule. When the nuclear mass M = 2.0 m_p, the time window lasts 16.0 fs; when M = 24.0m_p, the time window lasts 53.8 fs, as shown in Fig. 4(b). So only the THz pulse is suitable for the dissociation control of a heavy molecule, no other laser pulse has such a long half period and also a high peak intensity (3.8× 10¹² W/cm²) now.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Calculated results with the coupled equations (7). Asymmetry parameter A of changes with different wavelengths of the control pulse. All the asymmetry parameters become stable after about 16.0 fs, even though the pulse is very long. (b) The effective time (TW) for dissociation control as a function of the molecule mass M.

Figure 5 shows the largest probability of electrons on the ψ _r proton (the right nucleus) by adjusting the time delay dt between the pre-excitation of the Gaussian-type wave packet and the envelope peak of the THz pulse (25.6-μ m), with the nuclear mass of the molecule M = 2.0m_p, 16.0m_p, 32.0m_p.^[18] For , when dt = 49.2 fs, more than 99.7% of all the electrons can be controlled onto the ψ _r state, as shown in Fig. 5(a). For M = 16.0m_p, more than 99.5% of all the electrons localize on the right nucleus when dt = 28.5 fs, as shown in Fig. 5(b). for M = 32.0 m_p, the effective time is more than 60.8 fs, which is larger than the half period of the THz pulse that we chose, which lasted 42.7 fs, as shown in Fig. 5(d). The largest control ratio can only be achieved at some fixed time delay points. For example, when dt = 10.6 fs, one can obtain the largest localization ratio of the right nucleus, which can only reach 93.6%, as shown in Fig. 5(c). We have simulated that when the wavelength of the control pulse is doubled, more than 99.5% of all the electrons can be controlled to the right nucleus for M = 32.0 m_p.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Calculated results of the probabilities of electrons on states ψ g, ψ u, ψ l, and ψ r with the coupled equations (7). The mass of the molecule and the time delay between the pre-excited Gaussian-type wave packet and the THz pulse are (a) M = 2.0mp, dt = 49.2 fs; (b) M = 16.0mp, dt = 28.5 fs; and (c) M = 32.0mp, dt = 10.6 fs. (d) The THz pulse utilized throughout this paper.

We have shown that the extremely high electron localization can also be achieved in the dissociation of HD⁺ and HT⁺ as that in by using two laser pulses of UV and THz spectral regimes. The curves of dissociation asymmetry parameter A and ionization probability I of these three homo- and hetero-nuclear molecule ions vary the same with the time delay of the two pulses Δ t and the electric field strength of the UV pulse E₂₀. The electron localization effective time, which increases with the increasing nuclear mass of the homo-nuclear molecule, is almost the same for and its isotopes. By adjusting the time delay, more than 93.6% of all the dissociative events can be controlled to the pointed nucleus, though the molecule is 16.0 times heavier than . If the laser wavelength is long enough, the requirement for the laser intensity can be lower, leading to much lower ionization probabilities. Thus, the proposed scheme paves a new approach to efficiently control the electron localization in molecular dissociation.