Corresponding author. E-mail: daicj@126.com
Project supported by the National Natural Science Foundation of China (Grant No. 11174218).
The radiative lifetimes of the Eu 4f76s np (8P J or10P J) Rydberg states with J = 5/2 and 11/2 are investigated with a combination of multi-step laser excitation and pulsed electric field ionization, from which their dependence on the effective principal quantum number is observed. The lifetimes of 21 states are reported along with an evaluation of their experimental uncertainty. The influence of blackbody radiation, due to the oven temperature, on the lifetime of the higher- n states is detected. The non-hydrogen behavior of the investigated states is also observed.
A number of studies of Rydberg atoms have been reported in the past decade.[1– 5] In addition, much attention has been given to the lifetimes of Rydberg states of both alkaline-earth[6– 9] and rare-earth atoms.[10– 13] Although laser-induced fluorescence (LIF) is a popular method for lifetime studies, [14– 17] it is appropriate only for the lower excited states or the lower members (n < 20) of the Rydberg series. Since the lifetime of the Rydberg state increases approximately as n3, the fluorescence due to spontaneous emission becomes very weak for the higher members (n ≥ 20) of the Rydberg series. Therefore, the method of electric field ionization (EFI)[18– 21] is more suitable for measuring the lifetime of an atom in the Rydberg state.[22] By adjusting the time delay between the electric-field pulse and laser pulse, the lifetime of a Rydberg atom can be determined simply, efficiently and selectively by observing its decay rate.
Based on the fact that the lifetime of a Rydberg state is much longer than that of a valence state, especially near the ionization limit, it is possible with EFI to identify a valence state from a Rydberg series, while, in the framework of spectroscopy, this is a challenge. We accomplished this in the present work, providing an alternative technique to distinguish valence states from a Rydberg series.
In order to study the lifetime of the high-n states of the Eu atom near its 6s ionization limit, it is advantageous to choose the 4f76snp Rydberg states, as their n values were determined previously.[18, 23, 24] Specifically, the radiative lifetimes of the 4f76snp (8PJ or 10PJ) Rydberg states with J = 5/2 and 11/2 of Eu atoms were investigated in the present work with the combination of multi-step laser excitation and the EFI method.
The experimental approach is given in Section 2, while the experimental results and discussion are presented in Section 3. Finally, the conclusions are given in Section 4.
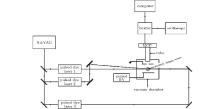
The experimental setup used in our investigation is shown schematically in Fig. 1. It consists mainly of three parts: a laser system, an atomic beam production system, and a data acquisition system.
More specifically, the laser system consists of three tunable dye lasers pumped by the second- or third-harmonic generation (SHG or THG) of the same Nd:YAG pulsed laser (Quanta System GNT 0021) at wavelengths of 532 nm and 355 nm, respectively. In order to make the three dye lasers sequential in time, the pulses of the second and third dye lasers are delayed by 10 ns and 20 ns relative to that of the first dye laser, controlled with a pulse generator (AVTECH AVRH-3-B). Typically, the dye laser has a pulse duration of 8 ns, line width of 0.1 cm− 1, and pulse energy of 0.5 mJ.
The atomic beam production system, inside a vacuum chamber with a typical pressure of about 10− 5 Pa, is composed of an atomic oven, a heating facility, and a beam collimator. The atomic oven is heated resistively by a direct current (DC) power supply to a temperature at 760 K, which is monitored by a controller with a platinum-rhodium thermocouple attached to the oven.
The data acquisition system includes a micro-channel plate (MCP) detector with a DC high-voltage (HV) power supply, a pulsed HV power supply, digital oscilloscope (Tektronix TDS3034B), and an integrated boxcar, whose output is sent to a computer for further analysis.
To avoid Doppler broadening, the atomic beam is collimated and directed to a region between the two parallel electric-field plates, 1-cm apart, where it is crossed perpendicularly by the three laser beams, which enter the vacuum chamber collinearly. A HV pulse of the electric field is applied to the plates 0.5 μ s after the laser pulses to avoid the Stark effect. The EFI signal is amplified by the MCP, averaged by the boxcar, and recorded by a computer with data acquisition software.
With stepwise excitations based on the resonant dipole transitions, a Rydberg atom can be produced efficiently, and its lifetime can be determined with the EFI method. In order to populate the 4f76snp (8PJ or 10PJ) Rydberg states, two different excitation schemes were designed for the experiment. With the two different intermediate states, 4f76s7s 8S7/2, 9/2, the two possible Rydberg series, 4f76snp (8PJ or 10PJ), can be excited, [18] namely
Scheme I (for J = 5/2, 7/2, or 9/2)
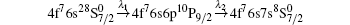
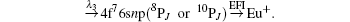
Scheme II (for J = 7/2, 9/2, or 11/2)
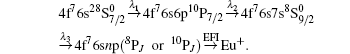
In scheme I, λ 1 = 686.4 nm, λ 2 = 668.5 nm, and λ 3 = 617– 625 nm, while in scheme II, λ 1 = 710.6 nm, λ 2 = 680.3 nm, and λ 3 = 590– 594 nm. The Eu atomic beam passes the interaction region between two parallel plates, where it crosses the three laser beams. Whenever the three-step excitation, either I or II, is completed, the Rydberg atom, with a large effective quantum number n*, can be ionized with a delayed high-voltage pulse applied to the plates, as shown in Fig. 2.
 | Fig. 2. The two excitation schemes for measuring the lifetime of Eu 4f76snp (8PJ or 10PJ) Rydberg states, where J = 5/2, 7/2, or 9/2 and 7/2, 9/2, or 11/2, respectively. (a) Scheme I, (b) scheme II. |
Based upon the J selection rules of the two excitation schemes, a comparison of the two EFI spectra from the two excitation schemes may help one to distinguish those 4f76snp (8PJ or 10PJ) Rydberg states with J = 5/2 and 11/2, respectively.[13, 18, 19]
To obtain the lifetime of a Rydberg atom, several parameters of the pulsed HV power supply have to be adjusted: first, the Rydberg atoms in the state with the effective quantum number n* can be field-ionized if the strength of the pulsed electric field is higher than the EFI threshold, namely, F0 = 1/[16(n*)4], in atomic units; secondly, the time delay between the EFI pulse and the laser pulses should be adjusted properly in order to avoid Stark effects, which can be controlled by the digital pulse generator, triggering the laser pulses, pulsed HV power supply and the gate of the boxcar integrator simultaneously. Meanwhile, the progression of the lifetime, τ , makes the EFI signal of the Rydberg atom decrease exponentially as time passes, i.e.,
 |
Thus, the lifetime of a Rydberg atom can be determined by fitting the experimental data to Eq. (1). The lifetime of an atom is dominated by the process of spontaneous emission, with a probability of radiative transition, Aif, where i and f denote the initial and final states of the decay, ignoring other processes, such as collision, or blackbody radiation (BBR). Thus, the lifetime of the Rydberg atom can be expressed as
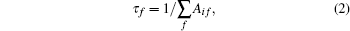 |
where the summation is for all the possible final states of the decay.
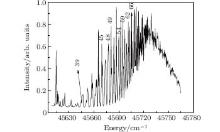
In order to obtain the lifetimes of the Eu 4f76snp Rydberg states, whose level energies should be determined in advance, the EFI spectrum of Rydberg states has to be measured, an example of which is shown in Fig. 3.
As stated earlier, by comparing the two spectra from schemes I and II, the even parity Eu 4f76snp Rydberg states can be observed and classified into two Rydberg series with J = 5/2 and 11/2, respectively. Their principal quantum number n, relative to the first ionization limit of the Eu atom, can be determined.
It is well known that lifetimes of Rydberg states with different n* in an independent Rydberg series can be scaled as 1/n*3, where n* is the effective quantum number. However, due to the mixture with the other Rydberg series and valence states, the quantum defects of Eu 6snp Rydberg states are no longer constants.[13, 18, 19] Such complicated effects result in a fluctuation of the EFI threshold of different n states from the scaling law with the s leading to the variation of the EFI signal from state to state, as can be seen from Fig. 3. Meanwhile, since the density of states is proportional to the n3, the energy gap of two states with the successive n values can hardly be resolved near the ionization limit, as shown in Fig. 3. Thus, only some of the observed states are chosen for lifetime measurement with the EFI technique. It is worth mentioning that the LIF technique is not suitable here, due to the long lifetimes.
Armed with the EFI spectra of Eu 4f76snp Rydberg states, the decay of ionization signal with the time delay between the EFI pulse and the laser pulses can be observed for each 4f76snp state so as to obtain its lifetime. Taking the 4f76s28p state at E = 45541.85 cm− 1 as an example, as shown in Fig. 4, each data point represents an average of 300 samples of the ionization signal with an uncertainty of about 10%. The lifetime of the given state is obtained by fitting the data to Eq. (1), as shown in the upper right corner of Fig. 4, where the decay curve is from the best fit. The measured lifetime for the given state is 3.907 μ s, from the best fit, as shown in Fig. 4. Similarly, lifetimes for the other states in the same 4f76s (9S) np series can be measured in the same manner.
To find out the general trend of the lifetimes within the same 4f76s (9S) np Rydberg series and compare lifetimes between the different 4f76s (9S) np series, the lifetimes of Rydberg states belonging to two different Eu 4f76snp(8PJ or 10PJ) Rydberg series (with J = 5/2 and J = 11/2, respectively) are studied systematically. Based upon their level energy and the n assignment given by our previous work, [13, 18, 19] the lifetimes of 4f76s (9S) np Rydberg states are measured.
It is helpful to list the scaling coefficient for the lifetimes of 4f76snp (8PJ or 10PJ) states with J = 5/2, as shown in the last column of Table 1.
| Table 1. Lifetime of 4f76snp (8PJ or 10PJ) Rydberg states with J = 5/2. |
The results in the last column of Table 1 deviate greatly from the scaling law, indicating that 4f76s (9S) np series is by no means an independent series. This is as expected: many Rydberg series converge to the two 6s and several 5d ionization limits, so these series may interact heavily. The great deviation from the 1/n*3 scaling law confirms that there is a significant perturbation of the lifetimes of the 4f76s (9S) np Rydberg states.
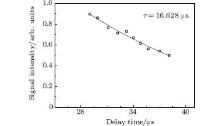
Turning to a lifetime of 4f76snp (8PJ or 10PJ) states with J = 11/2, figure 5 shows another example of lifetime measurements. A typical decay curve of the ionization signal is shown with a delay time for the 4f76s45p state at E = 45668.98 cm− 1. The lifetime obtained by the best fit from the attenuation curve is noted in the upper right corner of Fig. 5. Again, each data point in the figure is an averaged value of 300 samples of the ionization signal.
The data points fluctuate around the decay curve from the best fit, as shown in Fig. 5, and in contrast with Fig. 4. A possible explanation for this fact is as follows: since the lifetime of the 6s45p state is much longer than that of the 6s28p state, the time delay between the photo-excitation pulse and the EFI pulse has to be extended substantially, during which some Rydberg atoms may fly away from the collecting zone, resulting in the measured lifetime being less than the true value.
More lifetimes of Eu 4f76snp (8PJ or 10PJ) states in the same Rydberg series with J = 11/2 were measured, as shown in Table 2.
| Table 2. Lifetime of 4f76snp (8PJ or 10PJ) Rydberg states with J = 11/2. |
From Table 2, the configuration interactions among the different series are obvious, as shown in the last column of Table 2. Although the lifetime increases monotonically with the energy level, they fluctuate around the n*3 scaling law due to the configuration interaction. Since the lifetimes of the 4f76snp Rydberg states are much longer than those of valence states converging to the 5d ionization limits, the non-constant coefficient in the last column of Table 2 reflects a heavy perturbation from the valence states.
Now, let us turn to comparing the two 4f76snp Rydberg series with J = 5/2 and J = 11/2, respectively. Based upon the last columns of Tables 1 and 2, it is obvious that the departure from the scaling law differs for the two Rydberg series, as shown in Fig. 6. A possible explanation for this difference will be given below.
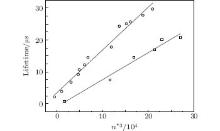 | Fig. 6. The dependence of lifetime on n* 3 for the 4f76snp(8PJ or 10PJ) Rydberg state; the dots and squares represent the J = 5/2 and J = 11/2 series, respectively. |
In Fig. 6, the solid lines are from the best fit to the experimental data listed in Tables 1 and 2. Several phenomena need to be addressed: first, for both 4f76snp Rydberg series, the departure from the scaling law of τ with n3 is obvious, reflecting significant non-hydrogen behavior; second, it is evident that the departures from the scaling law differ for the two series with J = 5/2 and J = 11/2. That is, the lifetimes of the 4f76snp Rydberg states are more sensitive to n for the J = 5/2 series than for the J = 11/2 series.
Lastly, let us consider the possible effect of the blackbody radiation (BBR), which is generated due to the temperature of the atomic beam. Substantially lower values would be predicted by the scaling law and are observed for the highest states in both series, as shown in both Tables 1 and 2, as well as in Fig. 6. At an operating temperature of approximately 800 K, the BBR may induce transitions between the different Rydberg states, an additional type of transition to the given EFI process, leading to the unrealistically short measured lifetimes. This effect naturally causes an additional error in the lifetime experiment, especially for those states with high principal quantum numbers, which explains the deviation from the scaling law for the highest states.
The radiative lifetimes of the Eu 4f76snp (8PJ or 10PJ) Rydberg states have departed from the scaling law of τ with n3, reflecting obvious non-hydrogen behavior. The lifetimes of the 4f76snp Rydberg states are more sensitive to the n value for the J = 5/2 series than for the J = 11/2 series. The study has demonstrated that blackbody radiation, which is due to the temperature of the atomic beam, may cause unrealistically short measured lifetimes, especially for those states with high principal quantum numbers.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|