Corresponding author. E-mail: liuhongping@wipm.ac.cn
Project supported by the National Basic Research Program of China (Grant No. 2013CB922003) and the National Natural Science Foundation of China (Grant Nos. 11174329 and 91121005).
We have studied highly excited sodium in various electric fields, parallel electric and magnetic fields, with one σ and π photon irradiation, and even in a magnetic field with a complex laser polarization configuration. The σ spectra shows a simple linear Stark effect with the applied electric field, while the π spectra exhibits a strong non-linear dependence on the electric field. The π transitions in parallel fields show a similar behavior to that in a pure electric field but the spectra get more smooth due to the magnetic field. The diamagnetic spectrum with laser polarization angles between 0 and π/2 proves that it can be reproduced by simple linear combination of π and σ components, indicating there is no interference between the π and σ channels. A full quantum calculation considering the quantum defects accounts for all the observations. The quantum defects, especially for the channel np, play an important role in the spectral profile.
The study of Rydberg atoms in external fields has drawn intensive interest in research communities and many new phenomena were identified.[1– 6] These phenomena are closely related to many fundamental problems, such as solving the nonseparable system and quantum manifestation of classical chaos. Compared with hydrogen, experiments of alkali-metal atoms in external fields show many new features due to the core-induced interactions.
Strong electric field has been applied to investigate the external effects of sodium for the lower excited Rydberg states (n < 20). The energy level splitting and shift of the lowly excited atoms (n = 15) in static electric fields of 0 up to 8000 V/cm has been studied by scanning the Stark map.[1, 6– 10] In 1976, Littman et al. reported experimental results of sodium with principal quantum number n = 15 in electric fields from 0 to 4 kV/cm and interpreted the anticrossing structure by diagonalizing the energy matrix.[1] In 1979, Zimmerman et al. presented a detailed study of Stark structures for all alkali metals in states around n = 15.[7] Afterwards, theoretically, Menendz reinvestigated the Stark map for Li, Na, and K with a novel method — quantum defect orbit in 2003.[8] At the same time, a resonance structure above the classical, even zero-field ionization limit in electric fields of several kilovolts per centimeter has been observed. For instance, in 1978, Freeman et al. observed systematic resonances above the zero-field limit for Rb in the presence of an electric field.[6] Then, Luk et al. observed the spectral features of sodium below the zero-field limit and the Fano line profiles due to the coupling between different channels.[11] Gao et al. investigated the photoionization cross sections for hydrogen and sodium in a strong electric field with the visualized closed-orbit theory.[12, 13] An interesting phenomenon of interference at the crossings of Stark resonances for sodium has been observed.[9] The interference leads to a striking line narrowing in the photoionization spectrum in the electric field, and the spectrum shows a Fano-like profile.[14]
The photoabsorption spectrum in external fields has also been studied theoretically. Semi-classical calculation employing the closed orbit theory can present a visual picture for the dynamic movement of the Rydberg electron in external fields.[12, 13, 15, 16] For example, Gao et al. recover the main spectral features of sodium in an electric field although the sharp oscillation in the spectrum remains unexplained.[13] As the effects of the external fields on the Rydberg electrons and the Coulombic attraction arising from the atomic core are of the same order, more critical quantum theory is crucial to achieve accurate computation. One of the most successful methods is the R-matrix combined with a complex coordinate method.[17, 18] In the R-matrix theory, the core effect has been absorbed into Bloch spherical wavefunctions, which are parameterized by the corresponding quantum defect values of different angular momentum channels. In the calculation, the wavefunctions at the inner boundary have to be evaluated as input, although they are energy-dependent.
Rather than applying strong electric fields, we study the spectrum of sodium at excited states more than n = 30 in moderate fields (F ∼ 100 V/cm). The states at higher energy have a better approximation for decoupling of the spin and orbital angular momenta[19] and the spectra in this energy range can also show the same essential features at n = 15. We observed the anti-crossing phenomena due to the core effect even at an electric field of 0 ∼ 50 V/cm. Moreover, we studied the spectrum of sodium in parallel electric and magnetic fields, even in magnetic fields with complex laser polarization excitations. All the spectra are calculated with our newly developed quantum method combining the quantum defect orbit model and the B-Spline basis.[20, 21]
The experiment is performed on the same apparatus described previously, [21, 22] here we just summarize the main features and improvements. A sodium atomic beam spouted from a resistance-heated oven travels to the interaction region after being collimated by two pin-holes with diameters of about 2 mm. The beam direction is aligned along the magnetic field, and is intersected perpendicularly by a pulse laser beam. Such a geometry avoids the motional Stark effect completely since the velocity component in the perpendicular plane of the magnetic field is negligible. The intense and stable magnetic field is generated by a super-conducting magnet (Oxford Instruments), with the maximum magnetic field up to 4 T and a stability of better than 1 Gauss in the present measurement. Meanwhile, a pair of Stark plate meshes are placed at the crossing point of atom and laser beams, keeping the electric field along the magnetic field and atom beam as well. In such a configuration, we can observe the electric field, magnetic field and even the parallel-field spectra on the same apparatus.
The sodium atom is irradiated through one-photon transition into Rydberg states (n > 30) efficiently with a 10-ns pulsed laser in the intersection region. The laser wavelength is around 240 nm and the linewidth is approximately 0.15 cm– 1. The laser pulse is produced by the dye laser system (Lambda Physik, Scanmate 2E) pumped by a Nd:YAG (spectra physics) laser and subsequently frequency-doubled with a system-controlled barium borate crystal. The final excited states can be further selected by the polarizations of the laser beam tuned with the Soleil– Babinet compensator. The one-photon excitation scheme avoids the pollution and complications from the intermediate excited states in two-step or multi-step excitation configurations.[23] The Rydberg atoms are ionized by a pair of electric grids of high voltage after passing through the Stark region, and the ion fragments are accelerated and efficiently detected by a two-layer micro-channel plate situated at the end of the vacuum chamber. The ionization signal is monitored by an oscilloscope (Tektronix TDS1012) and recorded by a Z-Tec data acquisition card inserted into a personal computer. All collected data can be processed in real time. The data acquisition and the wavelength scanning are synchronized and controlled by integrated software running on a personal computer.
The calculation has been introduced in detail in our previous works, [20, 21, 24] here we only summarize the main steps. In the presence of external parallel electric and magnetic fields oriented along the z-axis, in atomic units by the convention, the non-relativistic Hamiltonian H for the Rydberg sodium atom can be written as follows:[20]
 |
where H0 is the Hamiltonian of an atom in the free field, Hmag and Hele are the interactions of the atom with the applied magnetic and electric fields, respectively. Vr is the Coulomb potential including the effects of core-induced electron screening, leading to the loss of analyticity for the Schrö dinger equation. Rather than using the model potential[25, 26] or the R-matrix method[18] including the quantum defects implicitly, we employ an equivalent form for the central field potential:[27, 28]
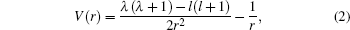 |
where λ = l − δ + Int(δ ) and the quantum defects are explicitly enclosed. Here Int(δ ) is the rounded nearest-integer value of the quantum defect. A reduced quantum defect δ ′ = δ − Int(δ ) is employed here to assess the real contribution of the quantum defect for a given angular momentum channel.
Solving the time-independent Schrö dinger equation
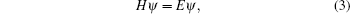 |
we can compute the transition probabilities corresponding to the experimental observations. For the atom in parallel electric and magnetic fields, we can expand the angular part of the wavefunction in the truncated associated Legendre function basis and the radial part in the B-spline basis
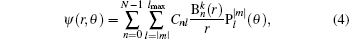 |
where 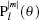
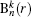
Substituting the Hamiltonian expressed in Eq. (1) and the wave function in Eq. (4) into Eq. (3), the Schrö dinger equation is transformed into a general eigenvalue problem
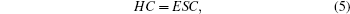 |
where E and C represent eigenvalues and their corresponding eigenvectors, respectively, H is the matrix form of the Hamiltonian, and S is the overlap matrix. Accurate matrix elements are obtained efficiently through the Gauss– Legendre integration scheme. A Lanczos algorithm for the general eigenproblem applied to the matrix equation can give the eigenvalue E and eigenvector C. The oscillator strength for the one-photon dipole transition from the initial state | i⟩ to the final state | f⟩ can be expressed as
 |
where d is the electric dipole operator.
For a direct comparison with our experimental spectrum, the theoretically calculated spectrum is convoluted with a Gaussian function (a full width at half maximum Δ G = 0.15 cm− 1) due to the Doppler broadening and the laser linewidth. In our calculation, we adopt quantum defects δ s = 0.348, δ p = 0.855, and δ d = 0.015 from Ref. [18], and the quantum defects for higher angular momentum states are very small and set to zero. The laser polarization can be rotated by the Soleil– Babinet compensator so that the sodium atoms are excited by absorption of π or σ photons. We can also polarize the laser in an arbitrary angle with the magnetic field, leading to a complex spectral structure. Limited by the laser linewidth and Doppler broadening, we have to choose a proper energy range to investigate the spectrum, where the line-splitting is large enough.
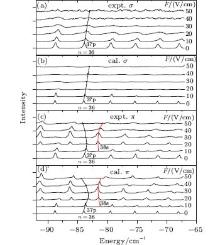
Figure 1 is the Stark spectra of sodium irradiated by one σ or π photon. Obviously, due to the symmetry limit, there is one missing for the spectral lines of the σ transition as shown in Fig. 1(a) compared with the π transition in Fig. 1(c). It can also be concluded from the interaction matrix elements, [35] i.e., for the σ transition to the np states, the matrix elements are zero. The quantum calculations are also presented in Figs. 1(b) and 1(d), corresponding to the experimental observations. They are in good agreement.
As the hydrogen approximation is broken immediately by the introduction of the quantum defect of np angular momentum states (δ p = 0.855), [36] the energy level will significantly red-shift compared to that of hydrogen. If applying an electric field for hydrogen, its Stark spectral lines for every n-manifold will get broad but keep symmetric. For our case of sodium, however, in weak electric fields, the np components are heavily populated and own strong spectral lines. The spectra for one n-manifold are not symmetric any more. Owing to the negative reduced quantum defects for np channels (δ p = − 0.145), the spectral lines at the high energy side will have stronger intensity. On the contrary, a numerical calculation shows that if the reduced quantum defects for np are positive, the lines at the low energy side will be more populated. This feature can be seen from the σ and π transitions in Fig. 1. At the same time, we can see that the σ transition has a linear Stark effect with the external electric field while the π transition shows a non-linear dependence on the electric field. Obviously, for the non-linear transitions, there exists an anti-crossing with other angular momentum channels, i.e., ns. This avoided-crossing exchanges their spectral line intensities, making the ns components populated at a higher electric field, which is shown in the curves labeled by 37p and 38s in Figs. 1(c) and 1(d). These phenomena are absent for the σ transitions.
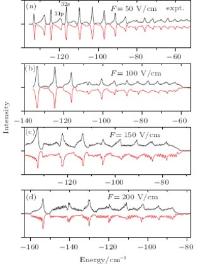
We show the π transition spectrum extended to the classical ionization limit[37] in Fig. 2 but in a much stronger electric field, up to 200 V/cm. In the spectrum of Figs. 1(c) and 1(d), the np and ns states exchange their spectral line intensities and even the ns states are more populated. This trend continues to prevail in electric fields beyond F = 50 V/cm, as shown in Fig. 2. As discussed in Figs. 1(c) and 1(d), with the electric field increasing, the spectral lines between np and ns turn to the directions so that they will not meet each other. When the electric field is increased further, for example, up to F = 200 V/cm, this kind of avoided crossing occurs again for the higher energy states but the spectral line intensities cannot be recognized clearly. Another feature is that the spectrum shows a saw-like fine spectral structure at fields up to F = 150 V/cm. According to the perturbation theory, the spectral splitting is approximately proportional to the electric field, i.e., δ E = 3nF/2. For the states around n ∼ 30 at weaker electric field F < 100 V/cm, the spectral splitting is less than or comparable to the line broadening 0.15 cm− 1 due to the Doppler and laser linewidth broadenings, resulting in the loss of the spectral resolutions.
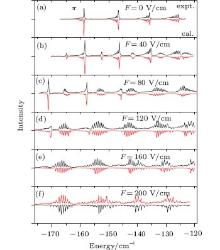
An interesting suggestion is to investigate how the Zeeman splitting lines in a magnetic field behave if a parallel electric field is applied. Keeping the laser pulse polarized as previously shown in Fig. 2, we apply a magnetic field of B = 2.5 T and study the spectral variation with the electric field. The experimental observations are shown in Fig. 3 as well as the corresponding calculations. At zero electric field, the spectral lines are split due to the magnetic field as shown in Fig. 3(a). When the electric field increases to F = 40 V/cm (shown in Fig. 3(b)), the manifold attributed to the same principal quantum number n is divided into two parts, the parent part shifts to higher energy with the electric field increasing while the other one shifts to lower energy. Increasing further the strength of the applied electric field, i.e., F = 80 V/cm as depicted in Fig. 3(c), the parent branch gets weaker and is comparable with the new-born one. Meanwhile, the new born lines get broad in energy, showing a Gaussian distribution in intensity. In a stronger electric field as shown in Figs. 3(d)– 3(f), the parent branches disappear and the new-born one predominates the main feature of the spectrum. This spectral character is similar to the case in a pure electric field shown in Fig. 2, but the introduction of a magnetic field depresses the abrupt lines in Fig. 2 and makes the spectrum more smooth. This is different from the case of lithium, where only the quantum defect for channel ns (δ s ∼ 0.4) deviates from zero significantly.[38]
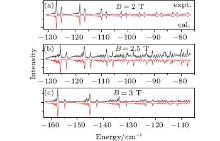
We also observed the magnetic rotation effect of the Glan– Taylor lens in the magnetic field. A Glan– Taylor lens is used to reflect our laser in the super-conducting magnet. The initial polarization of the laser pulse is perpendicular to the magnetic field, but this polarization is changed by the strong magnetic field, resulting in the laser excitation of the atom along and perpendicular to the magnetic field simultaneously. The spectra are recorded at B = 2 T, B = 2.5 T, and B = 3 T as shown in Figs. 4(a)– 4(c), respectively, corresponding to the rotation angles of 28, 25, and 20 degrees. Theoretically, we calculate the σ and π transitions firstly and compose the final spectrum with some certain ratios. For example, at B = 2 T, the σ : π ratio is 1:7, corresponding to an angle of 28 degrees, as shown in Fig. 4(a). It is similar to the observations for barium in a magnetic field.[24] The good agreement between the calculation and experiments also implies that there is no interference between the two channels. It is because the angular momentum projection on the magnetic axis is conservative and m is a good quantum number.
We have studied the highly excited sodium in various electric fields, parallel electric and magnetic fields with one σ and π photon irradiation and even in the magnetic field with a complex polarization configuration. The Stark spectrum shows a more complex structure than the diamagnetic spectrum due to the coupling between the neighboring channels, because the latter only couples the states Δ L = ± 2, keeping the channels ns and nd away. However, for all the cases we studied, the quantum defects for channel np play an important role for the spectral profile. Compared with the spectrum of hydrogen in a non-zero field, the spectral lines of sodium concentrate on the low field while they distribute in a wide energy range in a strong field. The π spectra exhibit a strong non-linear dependence on the electric field, even applying an additional magnetic field. In the latter case, the spectrum behaves more smoothly. The diamagnetic spectrum with polarization angle between 0 and π /2 proves that there is no interference between the π and σ channels, hinting that quantum interference can occur in crossed fields since these two channels are coupled in the Hamiltonian.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|