Cite this Article
Zhang Lu-Lu, Gao Shou-Bao, Meng Qing-Tian, Song Yu-Zhi. Accurate ab initio-based analytical potential energy function for S2 (ã1Δg) via extrapolation to the complete basis set limit* . Chinese Physics B, 2014, 24(1): 013101  
Permissions
Accurate ab initio-based analytical potential energy function for S2 (ã1Δg) via extrapolation to the complete basis set limit*
Zhang Lu-Lu, Gao Shou-Bao, Meng Qing-Tian, Song Yu-Zhi†
College of Physics and Electronics, Shandong Normal University, Jinan 250014, China

Corresponding author. E-mail: yzsong@sdnu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11304185 and 11074151).

Abstract

The potential energy curves (PECs) of the first electronic excited state of S2(ã1Δg) are calculated employing a multi-reference configuration interaction method with the Davidson correction in combination with a series of correlation-consistent basis sets from Dunning: aug-cc-pV XZ ( X = T, Q, 5, 6). In order to obtain PECs with high accuracy, PECs calculated with aug-cc-pV(Q, 5)Z basis sets are extrapolated to the complete basis set limit. The resulting PECs are then fitted to the analytical potential energy function (APEF) using the extended Hartree-Fock approximate correlation energy method. By utilizing the fitted APEF, accurate and reliable spectroscopic parameters are obtained, which are consistent with both experimental and theoretical results. By solving the Schrödinger equation numerically with the APEFs obtained at the AV6Z and the extrapolated AV(Q, 5)Z level of theory, we calculate the complete set of vibrational levels, classical turning points, inertial rotation and centrifugal distortion constants.

Keyword: 31.15.A–; 34.20.Cf; 31.50.Df; 33.20.–t; multi-reference configuration interaction method (MRCI); analytical potential energy functions; vibrational levels; spectroscopic parameters
1. Introduction

It has long been recognized that reduced sulfur-bearing species play an important role in the Earth’ s atmosphere, in biochemistry, and in combustion chemistry.[1, 2] Amongst the various reduced sulfur-bearing species, thiosulfeno radical HS2, [3, 4] hydrogen disulfide H2S2, [5] thiozone S3, [6, 7] etc. have aroused considerable interest. Diatomic sulfur S2, one component of these species, has also been investigated by many groups. Graham[8] was the first to observe the transition of the S2 state, and his work was followed by many attempts to interpret this heavily perturbed band system. The ground state of S2 was well characterized by a combination of electron paramagnetic resonance and microwaves.[9, 10] Employing a combination of cavity ring-down spectroscopy and model calculations, Wheeler et al. investigated the predissociation of the state[11] and the B– X band system of S2 over the range of excited state vibrational levels 10 < ν < 22.[12] Some of the accurate spectroscopic parameters and molecular constants reported in the literature prior to 1979 were summarized by Huber and Herzberg.[13]

Out of a vast body of theoretical work, by carrying out the ab initio calculations using self-consistent field (SCF) and configuration interaction (CI) with double zeta quality augmented with polarization functions, Swope et al.[14] studied the spectroscopic properties of thirteen low-lying electronic states of S2. Large scale CI calculations were carried out by Theodorakopoulos and Peyerimhoff[15] to investigate the properties of the , a1Δ g, and states of S2. Employing the B3LYP functional density theory, Mawhinney and Goddard[16] determined the spectroscopic parameters of these states. Denis[17] calculated the equilibrium geometry and the harmonic vibrational frequency of ground-state S2 using the coupled cluster theory. Utilizing the global potential energy surface (PES) of HS2(X A″ ) state, Song et al.[3] obtained more accurate spectroscopic parameters of ground-state S2. Most recently, Xing et al.[18] calculated the potential energy curves (PECs) of the ground and some excited states. It is known that S2 (ã 1Δ g) is involved in many reaction processes of sulfur-containing species, such as , etc. However, less effort has been put into accurately determining the analytical potential energy function (APEF) of S2(ã 1Δ g). So we are motivated to carry out more accurate theoretical investigations of S2(ã 1Δ g). It could serve as a reference for future studies on the above reactions and as a building block of the global PES for such molecular systems as HS2, H2S2, S3, etc.

In the present work, by utilizing the multi-reference configuration interaction including the Davidson correction (MRCI(Q)) method, [20] the PECs of the S2(ã 1Δ g) radical are calculated with a series of correlation-consistent basis sets from Dunning et al., [21, 22] i.e., aug-cc-pVXZ (X = T, Q, 5, 6), which are hereinafter denoted as AVXZ. The uniform singlet- and triplet-pair extrapolation (USTE) protocol[23] is employed to extrapolate the PECs calculated at AV(Q, 5)Z to the complete basis set (CBS) limit. All the PECs are then fitted to APEFs by using the extended Hartree– Fock approximate correlation energy method (EHFACE).[24] By numerically solving the radial Schrö dinger equation of the nuclear motion, the complete vibrational levels, classical turning points, inertial rotation and centrifugal distortion constants are calculated when the rotational quantum number J equals zero. The present results provide more accurate and complete spectroscopic information about S2(ã 1Δ g).

The paper is organized as follows. Section 2 describes the theoretical methods, including ab initio calculations, the procedure utilized to extrapolate the calculated energies and the APEF formalism. The results and discussion are presented in Section 3. While Section 4 gives our concluding remarks.

2. Theoretical methods
2.1. Ab initio calculations

All electronic structure calculations have been carried out at the MRCI(Q) level[20] using the full valence complete-active-space self-consistent field (CASSCF)[25] wave function as the reference, which has recently been applied to many diatomic molecules.[26– 28] The AVXZ (X = T, Q, 5, 6) basis sets of Dunning[21, 22] have been employed, and the calculations are carried out employing the MOLPRO 2012 package.[29] In the calculation, C2ν point group symmetry is adopted, which holds four irreducible representations, namely, A1, B1, B2, and A2. For S2(ã 1Δ g), four a1, two b1, and two b2 symmetry molecular orbitals (MOs) are determined as the active space, corresponding to the 3s3p shells of the sulfur atom in the CASSCF and MRCI(Q) calculation. This procedure involves 12 correlated electrons in eight active orbitals (4a1 + 2b1 + 2b2). For each basis set, the calculations of S2(ã 1Δ g) PECs are performed for the internuclear separation ranging from 1.2a0 to 20a0. Note that all the ab initio energies calculated at AVXZ (X = T, Q, 5, 6) basis sets are gathered in Table 1 of the Supplementary Material (SM). The core effects have been neglected by closing the core orbitals in the CASSCF and not correlating them in the MRCI(Q) calculation. A major reason for adopting the frozen core approximation lies in the fact that the raw ab initio energies calculated with relatively modest cost (AV(Q, 5)Z) are subsequently extrapolated to the CBS limit, denoted as CBS/AV(Q, 5)Z. The extrapolation is carried out via extrapolation of the electron correlation energy to the CBS limit plus extrapolation to the CBS limit of the CASSCF energy.

Table 1. Fitted parameters of S2(ã 1Δ g) APEFs in Eqs. (6) and (10).
2.2. Extrapolation to the CBS limit

The MRCI(Q) electronic energy can be treated in split form, which is written as[23, 30]

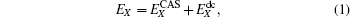where the subscript X indicates that the energy has been calculated in the AVXZ basis set, while the superscripts CAS and dc stand for the complete-active space and the dynamical correlation energies, respectively. The X = Q, 5 are adopted in the present work and denoted as USTE(Q, 5).

The CAS energies, which are uncorrelated in the sense of lacking dynamical correlation, are extrapolated to the CBS limit by adopting the two-point extrapolation protocol proposed by Karton and Martin[31]

where α = 5.34 is an effective decay exponent and is the energy when X→ ∞ .

The USTE protocol[23, 32] has been successfully applied to extrapolate the dc energies in MRCI(Q) calculations, which is written as

where A5 is determined by the auxiliary relation

Here A5 (0) = 0.0037685459, c = − 1.17847713, and α = − 3/8 are the universal-type parameters.[23, 29] Equation (3) is thus transformed into an (E∞ , A3) two-parameter rule, which is actually used for the practical procedure of extrapolation. The USTE extrapolation scheme has been shown to yield more accurate energies even when the extrapolation is carried out with the cheapest AV(D, T)Z pair.[32] Thus, it is utilized here to extrapolate the dc energies to the CBS limit for the title system.

2.3. APEF of S2(ã 1Δ g)

The diatomic PECs of S2(ã 1Δ g), which show the correct behavior at both the asymptotic limits R→ 0 and R→ ∞ , have been modeled using the EHFACE model, [24] which takes the following form:

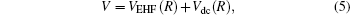where VEHF(R) and Vdc(R) denote the extended Hartree– Fock (EHF) and the dynamical correlation parts of the potential energy. The latter term is modeled by

with the damping functions for the dispersion coefficients assuming the form

where An and Bn are auxiliary functions and defined as

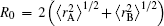
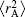
with α 0, β 0, α 1, and β 1 being universal dimensionless parameters for all isotropic interactions: α 0 = 16.36606, β 0 = 17.19338, α 1 = 0.70172, β 1 = 0.09574. Moreover, ρ /a0 = 5.5 + 1.25R0, is the LeRoy parameter, [33] and are the expectation values of squared radii for the outermost electron in atoms A and B, respectively.

The EHF-type energy term in Eq. (5) is written as

where γ = γ 0[1 + γ 1 tanh (γ 2r)], with r = R − Re, is the displacement from the equilibrium diatomic geometry; D, ai(i = 1, … , n), and γ i(i = 0, 1, 2) are adjustable parameters to be obtained from a least-square fitting procedure.

3. Results and discussion
3.1. The potential energy function

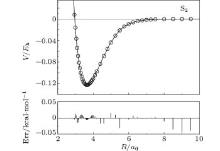
We compare in Fig. 1 the ab initio PECs of S2(ã 1Δ g) calculated at AV6Z and extrapolated to the CBS limit using AV(Q, 5)Z results. It can be seen that both PECs show a smooth and converged behavior. The difference between these two PECs is small, with the well depths of the global minimum differing only ∼ 0.001Eh. The AV6Z is considered an expensive basis set, with higher computational cost than AVQZ and AV5Z. With the extrapolation using the USTE(Q, 5) scheme, the accurate CBS PEC can be obtained at a much lower computational cost. Note that this extrapolation procedure was also successfully employed by Liu et al.[34] recently to obtain an accurate PEC of CO(X1Σ + ), with results comparing favorably with the experimental ones.

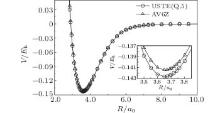Fig. 1. Comparison of the PECs of S2(ã 1Δ g) calculated at AV6Z and extrapolated to the CBS limit using AV(Q, 5)Z results.

The EHFACE model is then employed to obtain the APEFs for S2(ã 1Δ g) by least-square fitting the PECs calculated using AVXZ (X = T, Q, 5, 6). The APEF is also obtained by fitting the PECs extrapolated to the CBS limit using the result calculated from AV(Q, 5)Z basis sets, hereinafter denoted as CBS/USTE(Q, 5) APEF. The parameters ai, D, Re, and γ i are obtained from the least-square fitting procedure. We have tried n = 3 to n = 9 for the total numbers of coefficients ai with the purpose of getting a satisfactory result. By comparing the spectroscopic constants with the experimental and other theoretical data, the best results are obtained with n = 7. All parameters of APEFs for S2(ã 1Δ g) in Eqs. (6) and (10) are collected in Table 1, while the ab initio and the fitted CBS/USTE(Q, 5) PECs are displayed in Fig. 2. As can be seen, the modeled potential accurately mimics the ab initio energies, with the maximum error being smaller than 0.05 kcal/mol.

Fig. 2. The extrapolated CBS/USTE(Q, 5) PECs for S2(ã 1Δ g). The circles indicate the ab initio energies, while the line is from the fitted APEF. The differences between them are charted in the bottom panel.

To evaluate the fitting quality of the fitted PECs, we calculate the root-mean square derivation (Δ ERMSD) using the following equation:

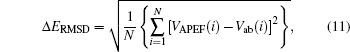where VAPEF(i) and Vab(i) are the i-th energies from fitting and from the ab initio calculation, respectively; N is the number of points employed in the fitting procedure (N = 79). The values of Δ ERMSD are also gathered in Table 1. This table shows the Δ ERMSD for APEFs obtained from fitting the ab initio PECs of MRCI(Q)/AVTZ, MRCI(Q)/AVQZ, MRCI(Q)/AV5Z, MRCI(Q)/AV6Z, and the extrapolated CBS/USTE(Q, 5) are 0.02201 kcal/mol, 0.2079 kcal/mol, 0.01860 kcal/mol, 0.01830 kcal/mol, and 0.01764 kcal/mol, respectively. The Δ ERMSD shows a decreasing trend as the size of the basis set increases, and the CBS/USTE(Q, 5) APEF gives the smallest RMSD, which shows that the fitting process is of a high quality.

Table 2. Spectroscopic constants compared with experimental and others’ theoretical data for the S2(ã 1Δ g) molecule. The dissociation energies are in Eh, equilibrium bondlength in a0, while Be, α e, and ω eχ e are in cm− 1.
3.2. Spectroscopic constants

Based on the APEFs obtained by fitting the raw MRCI(Q)/AVTZ, MRCI(Q)/AVQZ, MRCI(Q)/AV5Z, MRCI(Q)/AV6Z, and the extrapolated CBS/USTE(Q, 5) PECs, we calculate the spectroscopic constants of S2(ã 1Δ g). Some other theoretical and experimental studies have published spectroscopic constants of S2ã 1Δ g). Among them, Swope et al.[14] calculated Re, ω e, Be, and α e from the SCF and CI calculations. Compared with the experimental value, their vibrational frequency is too large. By carrying out the MRCI(Q) level of theory calculation with a series of Dunning’ s basis set, Peterson et al.[6] calculated Re, ω e and ω eχ e. Xing et al.[18] calculated the PECs of the ground state and some excited states, and gave more complete spectroscopic constants of S2(ã 1Δ g). The values of De, Re, ω e, Be, α e, and ω eχ e are collected in Table 2 together with the other theoretical and experimental data[13] for convenient comparison.[6, 14, 18] As we can see from the table, the dissociation energy increases monotonically as the basis set increases from AVTZ to AV6Z, and the largest value is obtained at CBS/USTE(Q, 5) APEF, differing 0.0012Eh from that at the AV6Z APEF. The equilibrium bond length is calculated from CBS/USTE(Q, 5) APEF to be 3.6007a0, which is only 0.0127a0 longer than the experimental value, [13] and 0.0035a0 longer than the most recent value obtained by Xing et al., [18] showing a high accuracy. The vibrational frequency is calculated to be 700.81 cm− 1, which differs from the experimental[13] and the theoretical[18] values by 1.54 cm− 1 and 1.13 cm− 1, respectively. The spectroscopic constant Be from CBS/USTE(Q, 5) APEF is smaller than that of Ref. [18], which must be due to the fact that Be is inversely proportional to Re. However, the spectroscopic constants α e and ω eχ e can be affected by Be, ω e, and the force constants (quadratic f2, cubic f3, and quartic f4). All of these parameters can cause the values of α e and ω eχ e to be larger than those of Refs. [6] and [18]. Comparing the results from the present CBS/USTE (Q, 5) APEF with those of AV6Z, the deviations of De, Re, ω e, Be, α e, and ω eχ e are 0.852%, 0.11%, 0.23%, 0.24%, 0.52%, and 0.38%, respectively. The spin– orbital coupling effect on the diatomic PEC and non-adiabatic reaction dynamics were investigated and reported in Refs. [35] and [36], as it is known that the spin– orbital coupling effect is big when crossing exists or the avoidance of crossing among the PECs. Although the spin-orbital coupling may affect the diatomic PECs and the spectroscopic constants, the spin-orbital coupling effect is not included in the current work, since we do not find the crossing or avoided crossing between the ã 1Δ g state and the ground state or the higher excited states.

It can be concluded from the above discussion that the present spectroscopic constants of the S2(ã 1Δ g) electronic state calculated from the CBS/USTE(Q, 5) APEF are in better agreement with the experiments and other theoretical results[6, 13, 14, 18] than those from the AVXZ (X = T, Q, 5, 6) APEFs. It is worth noting that the computational cost of the CBS/USTE(Q, 5) scheme is much lower than that of AV6Z, while it provides more accurate results.

3.3. Vibrational manifolds

By solving the radial Schrö dinger equation of the nuclear motion with the program Level 7.5, [37] we obtain the vibrational energy levels. The radial Schrö dinger equation of the nuclear motion is written as

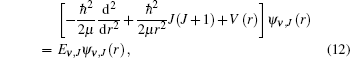where Ψ ν , J(r) and Eν , J are the eigenfunctions and eigenvalues of the potential 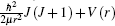, respectively, and V(r) is the rotationless APEF, r is the internuclear distance of diatom S2, μ is the reduced mass of the molecule, and ν and J are the vibrational and the rotational quantum numbers, respectively. For a given vibrational level, the rotational sublevels can be written as

where G(ν ) is the vibrational level, B(ν ) is the inertial rotation constant, and Dν , Hν , Lν , Mν , Nν , and Oν are the centrifugal distortion constants, respectively.

By solving Eq. (12) numerically, we obtain the complete set of vibrational states for S2(ã 1Δ g) when the rotational quantum number J equals 0. Due to the length limitation, we tabulate the results of only the first 21 vibrational states, while the complete set of vibrational states can be found in Tables 2 and 3 of SM. For each vibrational state, one vibrational level G(ν ) and its classical turning points, one inertial rotation constant B(ν ), and six centrifugal distortion constants Dν , Hν , Lν , Mν , Nν , and Oν are obtained. Table 3 presents the vibrational levels G(ν ), the classical turning points Rmin and Rmax, and the inertial rotation constants B(ν ) calculated from both the CBS/USTE(Q, 5) and AV6Z APEF. As we can see from Table 3, the CBS/USTE(Q, 5) APEF predicts slightly bigger vibrational levels G(ν ) than AV6Z APEF does. The difference is only 0.257 cm− 1 when ν = 0 and the difference becomes bigger as the vibrational number ν increases, with the largest difference being found to be 18.891 cm− 1 when ν = 20. The maximal difference for the inertial rotation constants B(ν ) is found at ν = 20 with the value of 1.93 × 10− 4 cm− 1. Moreover, the classical turning points differ at a magnitude of 10− 3a0, showing good accordance with each other.

Table 3. Vibrational levels G(ν )(in cm− 1), classical turning points (in a0), and rotational constant Bν (in cm− 1) of the first 21 vibrational states for S2(ã 1Δ g) when J = 0, predicted by the CBS/USTE(Q, 5) and AV6Z APEFs.

The other six centrifugal distortion constants Dν , Hν , Lν , Mν , Nν , and Oν obtained from the CBS/USTE(Q, 5) and AV6Z APEF are tabulated in Tables 4 and 5, respectively, with the difference between them being small. Unfortunately, as far as we know, there is no experimental or theoretical work reported on the vibrational levels, classical turning points, inertial rotation and centrifugal distortion constants. Thus, a direct comparison cannot be made between them. However, according to the high-quality fitting of the APEF and the excellent agreement between the present spectroscopic parameters and the available results reported in the literature, [6, 13, 14, 18] we have reason to believe that the results collected in Tables 4 and 5 are accurate and reliable. Furthermore, although the CBS/USTE(Q, 5) scheme is less costly, the APEF obtained from this scheme can give results as good as those at the AV6Z level. Thus the CBS/USTE(Q, 5) APEF can describe the interaction potential energy of S2(ã 1Δ g) well.

Table 4. Centrifugal distortion constants (in cm− 1) of the first 21 vibrational states for S2(ã 1Δ g) when J = 0, calculated from the CBS/USTE(Q, 5) APEF.
Table 5. Centrifugal distortion constants (in cm− 1) of the first 21 vibrational states for S2 (ã 1Δ g) when J = 0, calculated from AV6Z APEF.
4. Conclusions

The PECs of the ã 1Δ g electronic state of the S2 molecule have been calculated using the CASSCF as the reference wave function followed by the MRCI(Q) approach in combination with a series of correlation-consistent AVXZ (X = T, Q, 5, 6) basis sets. The USTE(Q, 5) scheme is employed to extrapolate the PEC to the CBS limit. The PECs so obtained are subsequently fitted to APEFs using the EHFACE model. Based on the APEFs of S2(ã 1Δ g), the spectroscopic constants De, Re, ω e, Be, α e, and ω eχ e are calculated. In comparison with the available experimental data, the results obtained from the CBS/USTE(Q, 5) and AV6Z APEF exhibit high accuracy. Thus, they are used to perform the calculations of vibrational manifolds. By numerically solving the radial Schrö dinger equation of the nuclear motion, the complete set of vibrational states have been obtained for the first time. For each vibrational state, one vibrational level and its corresponding classical turning points, one inertial rotation constant and six centrifugal distortion constants are also produced. As a whole, the present results provide a more accurate and complete investigations of the spectroscopic parameters and vibrational manifolds of the S2(ã 1Δ g) molecule.

Reference
1 Huxtable R J 1986 Biochemistry of Sulphur New York Plenum Press [Cited within:1]
2 Denis P A 2005 Chem. Phys. Lett. 402 289 DOI:10.1016/j.cplett.2004.12.001 [Cited within:1] [JCR: 2.145]
3 Song Y Z and Varand as A J C 2011 J. Phys. Chem. A 115 5274 DOI:10.1021/jp201980m [Cited within:2] [JCR: 2.771]
4 Denis P A 2006 Chem. Phys. Lett. 422 434 DOI:10.1016/j.cplett.2006.02.107 [Cited within:1] [JCR: 2.145]
5 Zhou C L, Sendt K and Haynes B S 2008 J. Phys. Chem. A 112 3239 DOI:10.1021/jp710488d [Cited within:1] [JCR: 2.771]
6 Peterson K A, Lyons J R and Francisco J S 2006 J. Chem. Phys. 125 084314 DOI:10.1063/1.2222367 [Cited within:6] [JCR: 1.578]
7 McCarthy M C, Thorwirth S, Gottlieb C A and Thaddeus P 2004 J. Am. Chem. Soc. 126 4096 DOI:10.1021/ja049645f [Cited within:1] [JCR: 10.677]
8 Graham J I 1910 Proc. R. Soc. London Ser. A 84 311 DOI:10.1098/rspa.1910.0077 [Cited within:1]
9 Wayne F D, Davies P B and Thrush B A 1974 Mol. Phys. 28 989 DOI:10.1080/00268977400102311 [Cited within:1] [JCR: 1.67]
10 Pickett H M and Boyd T L 1979 J. Mol. Spectrosc. 75 53 DOI:10.1016/0022-2852(79)90145-0 [Cited within:1] [JCR: 1.67]
11 Wheeler M D, Newman S M and Orr-Ewinga A J 1998 J. Chem. Phys. 108 6594 DOI:10.1063/1.476074 [Cited within:1] [JCR: 1.578]
12 Wheeler M D, Newman S M, Orr-Ewing A J and Ashfold M N R 1998 J. Chem. Soc. Faraday Trans. 94 337 DOI:10.1039/a707686j [Cited within:1]
13 Huber K P and Herzberg G 1979 Constants of Diatomic Molecules, Molecular Spectra and Molecular StructureVol. IV (Van Nostrand : Princeton) [Cited within:6]
14 Swope WC, Lee Y P and Schaefer III H F 1979 J. Chem. Phys. 70 947 DOI:10.1063/1.437484 [Cited within:5] [JCR: 1.578]
15 Theodorakopoulos G, Peyerimhoff S D and Buenker R J 1981 Chem. Phys. Lett. 81 413 DOI:10.1016/0009-2614(81)85641-2 [Cited within:1] [JCR: 2.145]
16 Mawhinney R C and Goddard J D 2003 Inorg. Chem. 42 6323 DOI:10.1021/ic0301270 [Cited within:1] [JCR: 4.593]
17 Denis P A 2004 J. Phys. Chem. A 108 11092 DOI:10.1021/jp047834e [Cited within:1] [JCR: 2.771]
18 Xing W, Shi D H, Sun J F, Liu H and Zhu Z L 2013 Mol. Phys. 111 673 DOI:10.1080/00268976.2012.741721 [Cited within:9] [JCR: 1.67]
19 Li A Y, Xie D Q, Dawes R, Jasper A W, Ma J Y and Guo H 2010 J. Chem. Phys. 133 144306 DOI:10.1063/1.3490642 [Cited within:1] [JCR: 1.578]
20 Werner H J and Knowles P J 1988 J. Chem. Phys. 89 5803 DOI:10.1063/1.455556 [Cited within:2] [JCR: 1.578]
21 Dunning T H 1989 J. Chem. Phys. 90 1007 DOI:10.1063/1.456153 [Cited within:2] [JCR: 1.578]
22 Woon D and Dunning T H 1993 J. Chem. Phys. 98 1358 DOI:10.1063/1.464303 [Cited within:2] [JCR: 1.578]
23 Varand as A J C 2007 J. Chem. Phys. 126 244105 DOI:10.1063/1.2741259 [Cited within:4] [JCR: 1.578]
24 Varand as A J C and Silva J D 1992 J. Chem. Soc. , Faraday Trans. 88 941 DOI:10.1039/ft9928800941 [Cited within:2]
25 Knowles P J and Werner H J 1985 Chem. Phys. Lett. 115 259 DOI:10.1016/0009-2614(85)80025-7 [Cited within:1] [JCR: 2.145]
26 Liao J W and Yang C L 2014 Chin. Phys. B 23 073401 DOI:10.1088/1674-1056/23/7/073401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
27 Cao Y B, Yang C L, Wang M S and Ma X G 2013 Chin. Phys. B 22 123401 DOI:10.1088/1674-1056/22/12/123401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
28 Li R, Wei C L, Sun Q X, Sun E P, Jin M X, Xu H F and Yan B 2013 Chin. Phys. B 22 123103 DOI:10.1088/1674-1056/22/12/123103 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
29 Werner H J, Knowles P J, Knizia G, Manby F R, Schütz M and others, MOLPRO, version 2012. 1, a package of ab initio programs; see http://www.molpro.net [Cited within:2]
30 Song Y Z and Varand as A J C 2009 J. Chem. Phys. 130 134317 DOI:10.1063/1.3103268 [Cited within:1] [JCR: 1.578]
31 Karton A and Martin J M L 2006 Theor. Chem. Acc. 115 330 DOI:10.1007/s00214-005-0028-6 [Cited within:1] [JCR: 2.233]
32 Varand as A J C 2000 J. Chem. Phys. 113 8880 DOI:10.1063/1.1319644 [Cited within:2] [JCR: 1.578]
33 Le Roy R J 1973 Spec. Period. Rep. Chem. Soc. Mol. Spectrosc. 1 113 [Cited within:1]
34 Liu Y F, Jia Y, Shi D H and Sun J F 2011 J. Quant. Spectrosc. Radiat. Transfer 112 2296 DOI:10.1016/j.jqsrt.2011.06.008 [Cited within:1]
35 Zhai H S, Zhang X M and Liu Y F 2013 Commun. Comput. Chem. 1 351 [Cited within:1]
36 Chu T S, Zhang Y and Han K L 2006 Int. Rev. Phys. Chem. 25 201 DOI:10.1080/01442350600677929 [Cited within:1] [JCR: 4.92]
37 Le Roy R J 2002 LEVEL 7. 5: A Computer Program for Solving the radial SchrÖdinger Equation for Bound and Quasibound levels, University of Waterloo Chemical Physics Report CP-655 (2002), available from http://leroy.uwaterloo.can/ [Cited within:1]