Corresponding author. E-mail: galashev@ecko.uran.ru
Atmospheric gases are ranked according to the efficiency with which they absorb and radiate longwave radiation. The open international HITRAN database of gaseous absorption lines of high resolution together with inverse Fourier transform were used. The autocorrelation functions of the total dipole moment of the basic greenhouse gases molecules such as H2O, CO2, O3, N2O, and CH4 were obtained. Absorption coefficient spectra and emission power spectra of infrared radiation of these gases were calculated. Analysis of the emissive ability of all gases under consideration was carried out. Compared to CO2, all the gases under investigation have more effective emission except ozone. An efficiency criterion of IR absorption and emission is defined and is calculated for each studied gas, and the gases are ranked accordingly as follows (from strong to weak): H2O, CH4, CO2, N2O, and O3.
In the atmosphere, the longwave radiation leaving the Earth is absorbed and re-emitted by greenhouse gases, clouds, aerosols and clusters. Energy transmission depends on the temperature and the ability of gas to absorb radiation of a given wavelength. The main greenhouse gases, such as water vapor, carbon dioxide, ozone, methane and nitrogen dioxide play a significant role in the regulation of the energetic balance of the Earth's atmosphere. In the presence of clouds, the energy transmission depends on the cloud cover, cloud thickness and the efficiency with which clouds can absorb and radiate longwave radiation. Radiative forcing in clear versus cloudy skies differs significantly.
HITRAN 2008 is the international database of gases' absorption lines of high resolution. It is used for the prediction and modeling of energy transfer in the atmosphere. There are descriptions of all essential lines of different isotopes for 42 molecules in the database.[1– 4] These lines are in both the IR[5, 6] and UV[7, 8] regions. There are line-by-line measurements[9– 11] and refraction coefficients of aerosols[12– 15] in the database. The data are obtained by remote sensing, by laboratory experiment and by simulation. For molecules of short-lived elements, the absorption cross section is calculated in laboratory conditions for temperatures of 200– 300 K.[16, 17] It should be noted here that in addition to the line's positions and its intensities, the contribution of gases to the energy balance depends upon both their height concentration profiles and their lifetime in the atmosphere.
The simulation of radiation transfer for an arbitrary composition of gases at temperatures of 100– 3000 K was executed using the HITRAN database.[18] Absorption coefficients up to heights of 25 km taking into consideration the height profiles of the principal greenhouse gases (water vapor, carbon dioxide, methane) are calculated.[19] Integral fluxes of longwave radiation are calculated. The use of spectroscopic data for radiation blocks of climate models is tested.[20] Model spectra of the transmission of a water vapor layer at atmospheric conditions are obtained. The transfer of high bandwidth-duration electromagnetic impulses in real atmosphere is studied.
The method of instantaneous normal modes[21, 22] used for experimental data processing gives an instantaneous scattering picture. This picture can show the structure and dynamic in both equilibrium and nonequilibrium states. The global minimum of potential energy corresponds to the state of the real physical system. In a nonequilibrium state, the lowest local minimum corresponds to the state of the real physical system. The received IR radiation absorption spectrum of ideal states will be denoted as σ iω (ω ). The HITRAN database is represented as σ iω (ω ) spectra. Using Monte– Carlo and molecular dynamics methods, there is no possibility to reach the global minimum of potential energy because of the insufficiency of calculation time and the number of chosen configurations. Consequently, there are modes characterizing nonstable transition through the energetic barrier in the model. Such transitions take place in the real Earth atmosphere. Their origin in that case is connected with nonstability of flowing processes. It can be seen on the multidimensional surface of potential energy as a negative curvature of its dependence on some degrees of freedom. In other words, there are modes with complex frequencies. As a rule, such modes are ignored, or an exponentially attenuating term giving structural relaxation is introduced. The IR radiation spectrum with transition modes will be denoted as σ (ω ). This σ (ω ) spectrum gives a more realistic picture of the Earth’ s radiation scattering in the atmosphere, because a number of complicated physical and chemical processes are taking place.
The goal of the present work is to investigate and analyze the emissive properties of the main greenhouse gases: H2O, CO2, O3, N2O, and CH4 using the experimental data of the open international HITRAN 2008 database, [23] to calculate the emission power spectra of IR radiation and to rank the investigated greenhouse gases according to the efficiency criterion of IR absorption and emission.
To receive and investigate emission power spectra of greenhouse gases and to calculate their emissive ability, it is necessary to solve the inverse task. By solving the inverse task we can receive power emission spectra of gases and calculate their emissive ability. Using the known IR absorption spectra from the HITRAN 2008 database[23] and applying the Fourier transform we can reconstruct an autocorrelation function of the molecule total dipole moment. There is a set of lines represented as the absorption intensities in units of cm− 1/(mol · cm− 2) in the HITRAN 2008 database. Here the frequency is in cm− 1, the scattering cross-section is in cm2, and normalization is per one molecule. A wide frequency range from 0 up to 5000 cm− 1 is covered. The frequency step is 0.001− 0.01 cm− 1. We chose the frequency range of 0 ≤ ω ≤ 3600 cm− 1 because the intensity of the Earth’ s emission spectrum at 3600 cm− 1 is no more than 0.1% of its maximum one. There are 60000 (N2O) and 125000 (CO2) values in the original number file. A data sample for the basic isotope is executed. Transformation of the line spectrum into the autocorrelation function is done for every frequency range separately because of irregular frequency steps for some spectra.
The autocorrelation function of the molecule total dipole moment can be calculated with the help of the Fourier transform according to the formula[24]
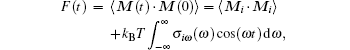
where M(t) is the sum of the real dipole moments of individual molecules at time t, Mi is a M quantity in the potential minimum of i mode, kB is the Boltzmann constant, T is a temperature corresponding to tropospheric or stratospheric conditions, and ω is a frequency of electromagnetic waves being absorbed. The first term is not taken into account because its influence is negligible at nonzero frequencies.[24] The density of states σ iω (ω ) has a positive value at any frequency.
Water vapor is a natural greenhouse gas that contributes more than 60% of the overall greenhouse effect. Moisture appears in the atmosphere as a result of evaporation from the Earth's surface. The low altitude layer below 5-km contains approximately 90% of the atmosphere's moisture. The quantity of moisture reduces with altitude. Water mass in the atmosphere is about 1.325× 1013 t. Though the atmosphere is hundreds of kilometers high, most of the air mass is located in a thin layer. Half of the atmosphere mass is located in the range between sea level and a height of 5– 6 km, 90% is in the layer up to 16 km and 99% is in the layer up to 30 km. The average concentration of H2O, CO2, CH4, and N2O in ppm in the 40-km layer of the Earth’ s atmosphere is represented in Table 1. Ozone concentration near the Earth's surface can reach 0.1 ppm. The O3 concentration can be up to 10 ppm at 10– 35 km height, where the ozone layer is located. The sum concentration of all gases under consideration does not exceed 1.1% of all atmospheric gases. The total atmospheric mass is 5.14 × 1018 kg. The average air molecular weight is 29 g/mol. So the total molecule number in the atmosphere is 1.067 × 1044. The layer of 40-km thickness contains about 1.056 × 1044 molecules. An estimated number of greenhouse gas molecules, obtained in accordance with each gas's average concentration, is given in Table 1.
Table 1. Concentration and average number  of molecules in the 40-km base layer of the Earth's atmosphere. of molecules in the 40-km base layer of the Earth's atmosphere. |
Lines intensity in the IR absorption spectrum is determined by the Bouguer– Lambert– Beer law
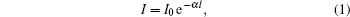 |
where α is an absorption coefficient and l is the thickness of the absorptive substance. In the SI system, the absorption coefficient characterizes the layer thickness of a substance, which attenuates the intensity of passing monochromatic radiation in e time. For fixed l, the smaller the α coefficient, the larger the intensity of IR spectra obtained by the experiment. Laboratory spectra give information about characteristic absorption frequencies and relative intensities of different greenhouse gases' spectra. The frequency spectrum α (ω ) of the absorption coefficient is more informative for quantitative estimation and physical characterization of the absorptive medium. The α (ω ) spectrum is an absolute characteristic of radiation absorption by the medium. IR spectra of the same gas under different conditions (laboratory experiment or real atmosphere) can differ significantly. IR spectra of real atmospheric gases are richer because of chemical interactions with atmospheric moisture and the presence of other components.
The imaginary part of dielectric permittivity ε " (ω ) is calculated from[25]
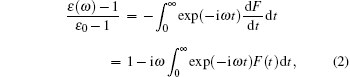 |
where ε 0 is static dielectric permittivity.
The absorption coefficient α of IR radiation of gases under investigation is obtained using the imaginary part ε " (ω ) in the form[26]
 |
where c is the speed of light.
The emitted power of IR radiation is calculated through the imaginary part of complex frequency-dependent dielectric permittivity ε (ω ) = ε ' (ω ) − iε " (ω ) according to the formula[27]
 |
where ⟨ E2⟩ is an average value of the square of the electric field strength.
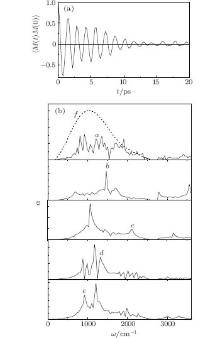
The autocorrelation function of the total dipole moment of nitrogen dioxide N2O, which has been reconstructed after Fourier transformation is shown in Fig. 1(a). Mutual compensation of contributions of the long sign variable "tail" tells about the reliability of spectral gases' properties calculated based on this function. Gases' absorption coefficients α (ω ) calculated using these functions are represented in Fig. 1(b) together with the Earth's radiation spectrum (curve f). This spectrum is obtained using radiation theory of a blackbody at an average temperature of the Earth's surface of 288 K. It is important to emphasize the fact that the HITRAN 2008 data consist of laboratory measurements, line parameters calculated from quantum mechanics, using the complete basis set method. In this case, it is necessary to do a correction of obtained α (ω ) spectra (as well as P(ω ) once to calculate the properties of greenhouse gases at conditions of the real atmosphere. Obviously, all greenhouse gases' molecules in the atmosphere take part in radiation energy exchange. In this case, the radiation absorption is determined by both dielectric properties of the molecules and emissive properties of the radiation source (i.e., by the frequency spectrum of the Earth's radiation). Every molecule absorbs (emits) incoming radiation at characteristic frequencies. Energy transformation by different greenhouse molecules goes proportionally to the intensity of the source radiation at characteristic frequencies. Correspondingly, the normalized spectrum of the Earth is supposed to be here as a weighting factor.
Water vapor absorbs IR radiation continuously in the frequency range of 0 ≤ ω ≤ 3600 cm− 1, with increased intensity in the range of 0 ≤ ω ≤ 2550 cm− 1 (Fig. 1(b), curve 1). The expended frequency range covers the most intensive (obtained experimentally[28]) absorption line of water vapor at 3400 cm− 1. There are absorption lines of all greenhouse gases in the reduced range. Spectra α (ω ) of gases, absorption coefficients are a continuous function of frequency with several lines of the highest intensity: 681, 1462, 1726, 3551 cm− 1 for CO2; 1060, 2118, 3150 for O3; split spectral lines (having two subpeaks) at 870 and 971, 1172, 1323 cm− 1 for CH4; 920, 1209 for N2O. There are faint spectral lines in α (ω ) gases' spectra also. They do not show significant absorption, but they are important for precise estimation of the greenhouse effect quantity.
The local atmospheric emission spectrum Pexp(ω ) in a frequency range of 600– 2000 cm− 1 is given in Fig. 2(a). It is experimentally obtained during a cold period with a clear sky and a zenith sun.[29] Measurements were executed with a Fourier spectrometer of 35 cm− 1 spectral resolution. There are emission lines of all basic greenhouse gases in this range. According to Fig. 2(a), the emission spectrum of atmospheric CO2 is located in a range of low frequencies that includes approximately 1/7 of the Earth's thermal radiation. The other 6/7 of intensity of the Earth's radiation spectrum falls to the frequency radiation range of other gases (O3, N2O, CH4, H2O). The integral intensity of the CO2 emission spectrum is 2.5 times higher than that for other greenhouse gases. In spite of that fact, carbon dioxide does not give highly effective radiation because the maximum of its emission spectrum is removed from the maximum of the Earth's emission spectrum by approximately 380 cm− 1 toward lower frequencies. The frequency ratio corresponding to the maxima of these two spectra is close to 0.63. Absorption of IR radiation by gas molecules is a complicated physical process. The average emission frequency ϖ of CO2 is 1.6 times lower than that of other gases under investigation. The energy efficiency of radiation received from CO2, which is proportional to ϖ , is five times lower than that of other gases.
 | Fig. 2 (a) Experimental spectra of gases, emission Pexp(ω ); [29] (b) calculated emission power of gases P(ω ): curve a: H2O; curve b: CO2; curve c: O3; curve d: CH4; curve e: N2O; curve f: spectrum of the Earth, s thermal radiation at T = 288 K. |
Emission power spectra of IR radiation P(ω ) in a frequency range of 0 ≤ ω ≤ 3600 cm− 1, calculated according to reconstructed autocorrelation functions of the total dipole moments of the gases' molecules, are shown in Fig. 2(b) (curves a– e). In the case of water (curve a), the spectrum is continuous across the whole range and significantly cut compared with the emission spectra of other gases, with 3– 5 fine peaks. Principal bands of the emission spectra of the gases under investigation fall into the frequencies in the Earth's radiation range: 1887 and 1947 cm− 1 for H2O, 659 and 1681 cm− 1 for CO2, 2093 cm− 1 for O3, 1174 cm− 1 for CH4, 1948 and 2238 cm− 1 for N2O. The spectrum of the Earth's thermal radiation at a temperature of T = 288 K is shown by curve f.
Additional bands in a calculated emission spectrum can appear because of the method of processing experimental data, overlapping effects (superposition of different gases’ spectra) and as a result of differences in atmospheric conditions of data from real physical experiments and laboratory measurements collected in the HITRAN 2008 database. Autocorrelation functions of the total dipole moment of the gas systems reconstructed according to the laboratory calculations give such effects.
Experimental data of emission flux for some bands of greenhouse gases emission spectra obtained according to the real atmospheric measurements are represented in Table 2.
| Table 2. Experimental values of emission flux for some bands of greenhouse gases’ emission spectra.[30, 31] |
For CO2, CH4, N2O, and O3[30] these measurements were carried out during a day in winter under conditions of a clear sky in Ontario province (Canada) and for H2O, [31] in subarctic regions during winter and summer. These measurements are the surface ones. In contrast, radiative forcing is calculated for the upper layer of the atmosphere. Disagreement of local values of emission flux with estimations of radiative forcing (given at the beginning of the work) is connected with that fact. In addition, the duration of experimental measurement plays a significant role. Molecules of H2O and CO2 have broad spectra with big values of emission flux. Emission spectra of CH4, N2O, and O3 molecules are characterized by separate strong bands.
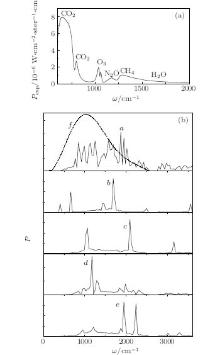
Ratios of the JP(GHG) emission integral intensities of gases under consideration in a frequency range of 0 ≤ ω ≤ 3600 cm− 1 to the JP(CO2) emission integral intensity of carbon dioxide (this gas was chosen as standard because of the possibility of its regulation and its broad distribution in the atmosphere, second to that of water vapor) are shown in Fig. 3(a), curve a. Analysis of relative emission intensity points out that water vapor has the biggest emission ability (strong greenhouse gas) and ozone has the smallest. (The main effect of ozone is to block out ultraviolet radiation but not to contribute to the greenhouse effect.) These characteristics are not connected with concentrations of greenhouse gases and they are determined by the electronic properties and the structure of molecules. Taking into account the Earth's thermal radiation spectrum (Fig. 1(b), curve f) and calculating emission integral intensities in the region defined by the Earth's radiation spectrum (0 ≤ ω ≤ 2550 cm− 1) we obtain curve c (Fig. 3(a)). The shape of this dependence is close to polygonal line a, excluding the fact that the relative emission intensity of water vapor decreases insignificantly and that of nitrogen dioxide increases. In relation to CO2, only ozone has less emission intensity (ratio JP(O3)/JP(CO2) < 1). Here methane and nitrogen dioxide are seen to be potentially dangerous greenhouse gases (because of the rapid growth of their concentrations in the atmosphere) in comparison with carbon dioxide. Straight lines b and d show the average values of ratios of emission integral intensities created by these gases for both cases.
Figure 3(b) shows the relationship of radiation integral intensities of greenhouse gases considering their concentrationsCGHG and of the carbon dioxide one CCO2: (JP(GHG)/JP(CO2))· (CGHG/CCO2) (polygonal lines a and c). In this case, greenhouse gases will be located according to their concentrations (see Table 1). No significant distinction in values determined by a and c polygonal lines (characterizing two frequency ranges) is observed, except for water vapor. Straight lines b and d show average values for four investigated gases.
Introducing an efficiency criterion of greenhouse gases, it is important to know both the frequency and intensity of absorption and the interaction mechanism between the molecule and the absorbed energy. Most of the absorbed energy is supposed to be re-emitted. If the frequency of re-emission is lower than that of absorption, then the emission of molecules will be spontaneous. This mechanism works for most greenhouse gases. The other important fact is the speed of energy re-emission by molecules. The faster a gas molecule re-emits absorbed energy, the earlier it absorbs a new portion of electromagnetic radiation and the greater its greenhouse effect is. Two factors are important in determining the efficiency of a greenhouse gas: the absolute value of absorbed energy and the exchange speed by electromagnetic radiation. A gas that absorbs and emits radiation rapidly is an effective one. Calculation of frequency dependence of α absorption coefficient of IR radiation gives the opportunity to determine Iα absorption integral intensity. Having the information concerning integral intensities of emission JP and absorption Iα , we can calculate the absolute efficiency of greenhouse gases β Pα = JP · Iα . We will investigate JP and Iα values in the ratio of absorption Iα (CO2) and emission JP(CO2) intensities of carbon dioxide. Relative greenhouse efficiency of gases is determined as β =(JP/JP(CO2))· (Iα )/(Iα (CO2)).
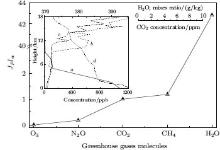 | Fig. 4. Greenhouse efficiency JPIα of investigated atmospheric gases. Inset: atmospheric height profiles of greenhouse gases' concentrations: curve a: water vapor; [22] curve b: ozone in winter; [23] curve c: ozone in summer; [23]curve d: carbon dioxide.[24] |
Figure 4 shows efficiency criterion β values of greenhouse gases. They are located in the figure as the value rises, β = 1 for CO2. If β > 1, then the gas is more effective and if β < 1, then the gas is less effective at creating the greenhouse effect than carbon dioxide. It is important to emphasize that methane can be considered here to be a strong greenhouse gas.
As mentioned above, the HITRAN 2008 data of IR radiation absorption are obtained during laboratory experiments at ambient temperature. Consequently, they are not connected with the real atmospheric conditions. To estimate the real contribution of each investigated gas to the greenhouse effect, it is important to take into account the height profiles of their concentrations. In the inset of Fig. 4, height concentrations of the basic greenhouse gases in the troposphere are shown: water vapor (curve a), [32] ozone during winter (curve b) and summer (curve c), [33] and carbon dioxide (curve d).[34] The concentration of H2O drops dramatically with height. The opposite situation is observed in the case of ozone: 5% of it is in the troposphere. Intensive growth of its concentration starts from 10– 12-km height and the maximum is found at 20– 25-km height. Concentrations of CO2, N2O, and CH4 decrease slowly with height. Emissive-absorptive ability of greenhouse gases in the troposphere influences the formation of the Earth's energetic balance.
Extraction of every gas´ s contribution into radiative forcing is difficult because of overlapping effects, i.e., different gases absorb at different wavelengths. We introduce an efficiency criterion of IR absorption and emission that characterizes the efficiency of the radiation distribution. The radiative forcing property describes the emission power of gases per 1 m2 and value β shows the correlation between absorption and emission of gases considering their concentrations. According to their calculated criterion value of relative greenhouse efficiency, the atmospheric gases are ranked as follows (from strong to weak): H2O, CH4, CO2, N2O, and O3 . In relation to CO2, all gases under investigation except ozone have more effective emission (their relations JP(GHG)/ JP(CO2) > 1). We need to emphasize the fact that methane and nitrogen dioxide should be considered as potentially more dangerous greenhouse gases.
In studying and making policies about the increasing influence of greenhouse gases in changes of the energetic balance of the Earth's atmosphere, the contribution of carbon dioxide is commonly overestimated. Carbon dioxide is usually considered to be the dominant greenhouse gas of anthropogenic nature. The estimation of water vapor's greenhouse effect varies because of clouds. They are located at 1.5– 3-km height and 60% of water vapor is located in exactly the same range. The underestimated role of methane is an important factor. Its concentration has been increasing more rapidly (up to 1.5% per year) than that of CO2 (1.1% per year). The retreat of permafrost and the melting and evaporation of wetlands produce methane from large areas, particularly in Western and Eastern Siberia. Squares of rice fields and the rise of petroleum extraction also contribute. If today's methane level increases by a factor of two, the temperature of the Earth's surface will increase by 0.3 K. This is a significant fact for the energetic balance of the Earth. Consequently, it is important to monitor and regulate not only CO2 gas but other greenhouse gases also (CH4, N2O, O3).
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|