Cite this Article
Zhang Rong, Xu Yun-Qiu, Xue Peng. Disordered quantum walks in two-dimensional lattices. Chinese Physics B, 2015, 24(1): 010303  
Permissions
Disordered quantum walks in two-dimensional lattices
Zhang Ronga),b), Xu Yun-Qiub), Xue Penga),c)†
Department of Physics, Southeast University, Nanjing 211189, China
School of Optoelectronic Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China

Corresponding author. E-mail: gnep.eux@gmail.com

Project supported by the National Natural Science Foundation of China (Grant No. 11174052), the National Basic Research Program of China (Grant No. 2011CB921203), and the Open Fund from the State Key Laboratory of Precision Spectroscopy of East China Normal University.

Abstract

The properties of the two-dimensional quantum walk with point, line, and circle disorders in phase are reported. Localization is observed in the two-dimensional quantum walk with certain phase disorder and specific initial coin states. We give an explanation of the localization behavior via the localized stationary states of the unitary operator of the walker + coin system and the overlap between the initial state of the whole system and the localized stationary states.

Keyword: 03.67.Lx; 05.40.Fb; 71.23.–k; 05.45.Mt; quantum walk; Anderson localization; phase disorder
1. Introduction

Quantum walk (QW) is the counterpart of the classical random walk (RW) in the quantum world.[1] The one-dimensional (1D) QW consists of a walker and a coin. The time evolution is described as follows. Firstly, the coin operator C is applied only on the quantum coin. Then the shift operator S= |x1⟩ w⟨ x|⊗ |0⟩ c ⟨ 0|+|x+1⟩ w⟨ x|⊗ |1⟩ c⟨ 1| is followed, which makes the walker move along the x axis according to the state of the coin. The shift operator entangles the coin and the walker. The QW is realized by successive coin flipping C and position shift S. The features of the QW are quite different from those of the RW[2– 5] due to the principle of superposition in quantum mechanics. The position variance σ 2 = ⟨ x2⟩ ⟨ x⟩ 2 of the QW is proportional to the square of the evolution time n2, which is called the ballistic behavior. Whereas, P of the RW is a Gaussian distribution. The position variance σ 2 is proportional to the evolution time n, which is called the diffusive behavior. The position variance represents the walker’ s spread velocity, the faster the walk moves, the bigger the value of the variance is. The spread velocity of the QW is faster than that of the RW. Powerful quantum algorithms based on the QW with higher efficiency have been devised.[6– 9] Besides the applications in quantum algorithms, the QW is also used as a tool to study the dynamics of complex systems, such as the energy transport in photon synthesis[10] and simulations of the formation of molecule states.[11] The QW provides insights into quantum phenomena, such as the Anderson localization[12– 15] and topological phases.[16, 17] The QW can be also used for the universal quantum computing[18– 28] and the state transfer.[18, 19, 29] The QW has been implemented experimentally in different physical systems, such as optical systems, [30– 39] NMR systems, [40– 42] trapped neutral atoms, [43, 44] and trapped ions.[45, 46]

The 1D QW can be extended to the 2D QW which includes a walker and two coins. The walker moves in a 2D square lattice according to the states of the two coins. One coin controls the walker’ s movement along the x direction and the other controls the walker’ s movement along the y direction. The whole Hilbert space of the 2D QW is 𝓗 c ⊗ 𝓗 w, where 𝓗 c is the four-dimensional coin space {|c1, c2⟩ } with c1, c2 ∈ (0, 1), and 𝓗 w= 𝓗 x ⊗ 𝓗 y whose basis is {|x⟩ ⊗ |y⟩ } (x, y ℤ ) corresponding to the walker’ s lattice space. Without loss of generality, we assume that the walker starts from position (0, 0). One step of evolution includes a coin flipping and a shift operation, and the unitary operator is

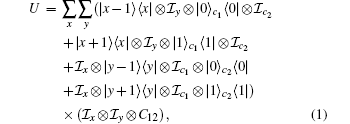where C12 is the joint operator on the two coins, ℐ x(ℐ y) is the identity operator on the walker along the x(y) direction, and ℐ c1 and ℐ c2 are the identity operators on the two coins. The influence of the decoherence and the disorder on the features of the QW has already been studied in Refs. [47]– [58].

The static disorder transforms the ballistic spreading of the 1D QW to localization due to the change of the interference pattern. Here we focus on the features of the 2D QW caused by inhomogeneity with the coin flipping C12= C1⊗ C2,

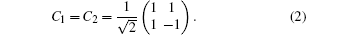The inhomogeneity is caused by the phase disorder at a certain point, line, or circle in the two-dimensional lattice, and we call the three types of phase disorders point, line, and circle disorders, respectively. The position distribution P(x, y) and the variance σ 2 are used to describe the features of the 2D QW with different types of phase disorders, and we also give an explanation of the localization effect in the following section. We find that the spreading velocity of the walker decreases in the 2D QW with proper initial state and phase disorder. Such features of the 2D QW are similar to the quantum resonance in quantum chaos and are helpful to study quantum chaos.

2. 2D QW with point disorder

The 2D QW with point disorder in phase is considered in this section. The walker moves in a two-dimensional square lattice according to the states of two coins and acquires an additional phase disorder eiϕ (ϕ = π ) at certain position (m, n). The unitary operator UP of the one step evolution is

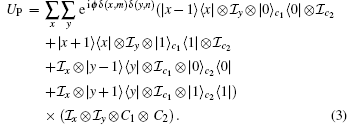2.1. 2D QW with point disorder at origin (0, 0)

The features of the 2D QW with point disorder at (0, 0) are discussed in details in this subsection. The position distribution of the 2D QW without point disorder for initial coin state |00⟩ is shown in Fig.  1(a), and the walker spreads far away from the original position. However, when the point phase disorder eiϕ (ϕ = π ) is added at (0, 0), the walker appears at (0, 0) with maximal probability after 50-step evolution, as shown in Fig.  1(b). This phenomenon is called localization. The distributions of the 2D QW with point disorder at (0, 0) for initial coin states |11⟩ , |01⟩ , and |10⟩ are similar to that for initial coin state |00⟩ . In this paper, we only discuss the case that the walker starts from the original position (0, 0). If we choose other initial separated coin states, such as (|0⟩ +i|1⟩ )(|0⟩ +i|0⟩ )/2 and (|0⟩ -i|1⟩ )(|0⟩ -i|0⟩ )/2, no localization effect can be observed in the 2D QW with point disorder at (0, 0). For the initial singlet entangled state of the coin without point disorder at (0, 0), the localization does not occur, as shown in Fig.  1(c). However, we observe the localization effect when the point disorder is added at (0, 0), as shown in Fig.  1(d). For the initial triplet entangled state of the coin , the localization effect is also observed. Whereas for other initial triplet entangled states of the coin and , no localization effect is observed in the 2D QW with point disorder at (0, 0). We have shown the distribution of the 2D QW with point disorder at (0, 0), and the localization is observed for specific initial coin states. If the point disorder is added at other positions except for (0, 0), the localization cannot be observed for any initial states.

Fig. 1. The distributions of 2D QW with point disorder eiϕ at origin (0, 0): (a) with ϕ = 0 (without phase disorder) for the initial separated state |00⟩ , (b) with ϕ = π for the initial separated state |00⟩ , (c) with ϕ = 0 (without phase disorder) for the initial entangled state , (d) with ϕ = π for the initial entangled state .

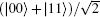
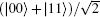
The localization effect is explained by analyzing the distribution property of the eigenstates of the unitary operator for the 2D QW with point disorder. If the initial state of the system |ψ ⟩ is one of the eigenstates of the unitary operator, then the state will stay unchanged. For the 2D QW without phase disorder, none of the eigenstates of the unitary operator exhibits localization. Thus the localization cannot be observed in the 2D QW without point disorder for any initial coin states. Whereas for the unitary operator of the 2D QW with point disorder ϕ = π at (0, 0), some of eigenstates |φ k⟩ exhibit localization, and we call such states the localized stationary states. 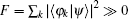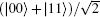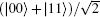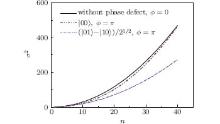If the overlap between the initial state of the walker-coin system and the localized stationary states , then the localization can be observed. The overlap F depends on the initial state and the unitary operator of the whole system. We calculate the overlap for different initial states |0⟩ x⊗ |0⟩ y⊗ |ψ ⟩ c. For initial separated coin state |ψ ⟩ c=|00⟩ (|11⟩ ), F=0.1760, whereas for initial separated coin states (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2 and (|0⟩ – i |1⟩ )(|0⟩ – i |1⟩ )/2, F=0. For entangled initial coin states and , F=0.7049, whereas for and , F=0. Thus we can explain the existence of localization in the 2D QW with point disorder at (0, 0) for initial coin states |00⟩ (|11⟩ ) and , as shown in Figs.  1(b) and 1(d). If the point disorder is acquired at other positions except for (0, 0), F=0 for all initial states. Thus the localization is not observed in the 2D QW with point disorder at other positions except for (0, 0).

The variance of the 2D QW can be expressed as σ 2(x)= ⟨ x2⟩ – ⟨ x⟩ 2 and σ 2(y)= ⟨ y2⟩ – ⟨ y⟩ 2. Numerical calculations show that σ 2(x)= σ 2(y). Thus we can use σ 2= σ 2(x) to describe the variance of the 2D QW. Figure  2 shows σ 2 as a function of the evolution time n for the 2D QW with point disorder at (0, 0) and different initial coin states. It is shown in the black line that the variance of the 2D QW without phase disorder increases with the evolution time n quadratically. The red dot-dot-dashed line corresponds to the 2D QW with point disorder at (0, 0) for the separated initial coin state |00⟩ , and the green dot-dashed line corresponds to the entangled initial coin state left . The rate growth of the variance for the 2D QW with point disorder decreases compared to that of the 2D QW without phase disorder, and the rate for the initial separated state |00⟩ is larger than that for the initial entangled state . The probability P(0, 0) for the entangled initial coin state is larger than that for the separated initial coin state |00⟩ after evolution in the 2D QW with point disorder at (0, 0), as shown in Figs.  1(b) and 1(d). So the spread velocity of the entangled initial coin state is slower than that of the separated state.

Fig. 2. The variance of 2D QW with point disorder eiϕ (ϕ =π ) at origin (0, 0) for different initial coin states. The black line corresponds to ϕ = 0 (without phase disorder) for the initial separated state |00⟩ ; the red dotted line corresponds to ϕ = π for the initial separated state |00⟩ ; and the green dot-dashed line corresponds to ϕ = π for the initial entangled state .

2.2. 2D QW with point disorder at two symmetric points (m, n) and (– m, – n)

We want to know whether the localization exists if the walker acquires the point disorder at two symmetric positions about (0, 0). The distributions of the 2D QW with point disorder at positions (1, 1) and (– 1, – 1) for different separated initial coin states and for different entangled initial coin states are shown in Figs.  3 and 4, respectively. We find that the 2D QW with point disorder added at two symmetric positions (1, 1) and (– 1, – 1) exhibits the localization effect for the specific initial coin states |00⟩ (Fig.  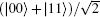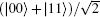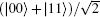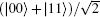3(a)) and (Fig.  4(a)). Whereas for the other initial coin states, there is no localization effect. For the 2D QW with point disorder at two symmetric positions (1, – 1) and (– 1, 1), there also exists the localization effect for the specific initial coin state . Whereas the 2D QW with point disorder at other positions (m, n) and (– m, – n) except for pair positions of (1, 1), (– 1, – 1) and (1, – 1), (– 1, 1) does not exhibit the localization effect. The localization effect can also be explained by analyzing the distribution property of the eigenstates of the unitary operator in this case. We calculate the distribution of the eigenstates of the unitary operator for the 2D QW with point disorder at two symmetric positions (1, 1) and (– 1, – 1). Some of the eigenstates show localization. For the separated initial coin state |00⟩ (|11⟩ ), the overlap between the initial state and the localized stationary states is F=0.0233. Whereas for (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2, and (|0⟩ – i |1⟩ )(|0⟩ – i |1⟩ )/2, F=0.0465. For the entangled initial coin state , F=0.0465. For , and , F=0. Thus for the initial coin states |00⟩ (|11⟩ ) and , the 2D QW with point disorder at (1, 1) and (– 1, – 1) exhibits localization as shown in Figs.  3(a) and 4(a).

Fig. 3. The distributions of 2D QW with point disorder eiϕ (ϕ =π ) at two symmetric positions (1, 1) and (– 1, – 1) for different separated initial coin states: (a) |00⟩ (|11⟩ ) and (b) (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2.

Fig. 4. The distributions of 2D QW with point disorder eiϕ (ϕ =π ) at two symmetric positions (1, 1) and (– 1, – 1) for different entangled initial coin states: (a) 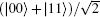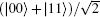, (b), (c) , and (d).

The variance of the 2D QW with point disorder eiϕ (ϕ =π ) at two symmetric positions (1, 1) and (– 1, – 1) for the separated initial coin states is shown in Fig.  5(a) and that for the entangled initial coin states is shown in Fig.  5(b). The σ 2 of the 2D QW without point disorder at two symmetric positions with (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2 is larger than that with |00⟩ for the same evolution time, as shown with the solid black line and the dashed green line in Fig.  5(a). In Fig.  5(a), it is shown that σ 2 with point disorder at (1, 1) and (– 1, – 1) is smaller than that without phase disorder for the same initial coin state and the same evolution time. Thus the point disorder at two symmetric positions decelerates the walker’ s spread velocity. However, σ 2 is the same for four different Bell entangled initial coin states as shown with the solid black line in Fig.  5(b). The σ 2 of the 2D QW without phase disorder is smaller than that of the 2D QW with point disorder at two symmetric positions for , and larger than that for the other three Bell entangled states at the same n. Thus the point disorder at (1, 1) and (– 1, – 1) usually decelerates the walker’ s spread velocity. While for a specific initial entangled state, the point disorder at two symmetric positions can increase the walker’ s spread velocity.

Fig. 5. The variance of 2D QW with point disorder eiϕ (ϕ =π ) at two symmetric positions (1, 1) and (– 1, – 1) for (a) the separated initial coin states and (b) the entangled initial coin states.

3. 2D QW with line disorder in phase

In this section, we discuss the properties of the 2D QW with line disorder in phase added along a specific line.

3.1. 2D QW with line disorder at the axis and line disorder paralleled to the axis

First, we consider the 2D QW with line disorder paralleled to the y axis. The walker acquires additional phase disorder eiϕ (ϕ =π ) when the walker is at line y=a (a ∈ ℤ ), and for a=0 the line disorder is added along the y axis. The unitary operator of the 2D QW with line disorder at y=a for one evolution time is

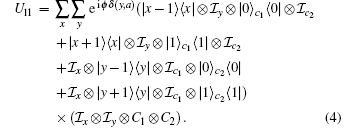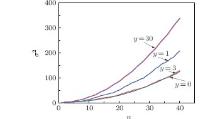
Numerical calculations show that the distributions of the 2D QW with line disorder at y=a are the same for different initial coin states. Figure  6 shows the distributions of the 2D QW with line disorder at y=0, y=1, y=3, and y=30. For the 2D QW with line disorder at y=0, the walker mainly stays near the line x=0, and the probabilities at other positions are nearly 0 as shown in Fig.  6(a). In Fig.  6(b), for the case with line disorder at y=1, the probabilities P(x, y) near line x=0 are decreased compared to those for the line disorder at y=0, and are still larger than the probabilities at other positions. For the line disorder at y=3, the probabilities P(x, y) near x=0 are decreased nearly to 0 and the walker spread far away from the origin in Fig.  6(c). With the line disorder at y=30 far away from the origin (0, 0), the distribution is similar to that of the 2D QW without line disorder, as shown in Fig.  6(d). It is shown in Fig.  6 that the further the line disorder is apart from the origin, the less the influence on the properties of the 2D QW.

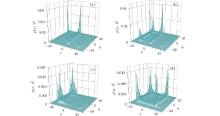Fig. 6. The distributions of 2D QW with line disorder eiϕ (ϕ =π ) at (a) y=0, (b) y=1, (c) y=3, and (d) y=30.

The variance of the 2D QW with line disorder at y=0, y=1, y=3, and y=30 as a function of the evolution time n is shown in Fig. 7. The variance of the 2D QW with line disorder at y=1 and y=3 is smaller than that at y=30 and larger than that at y=0 for the same evolution time n. This is because when the walker acquires the line disorder at y=0, he is mainly at line x=0 and the spread velocity is largely suppressed, whereas the walker’ s distribution with the line disorder at y=30 is almost the same as that of the 2D QW without the phase disorder and the spread velocity is nearly unchanged compared to that of the 2D QW without line disorder.

Fig. 7. The variance of 2D QW with line disorder eiϕ (ϕ =π ) as a function of the evolution time n.

3.2. 2D QW with line disorder at x=y

We consider another case with the line disorder at x=y passing through (0, 0). The unitary operator of the 2D QW with line disorder at x=y is>

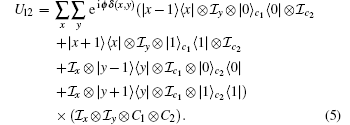The walker acquires the additional phase disorder eiϕ (ϕ =π ) at line x=y.

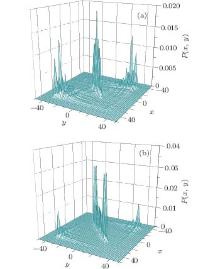The distribution of the 2D QW with line disorder at x=y for the separated initial coin state (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2 ((|0⟩ – i |1⟩ )(|0⟩ – i |1⟩ )/2) is shown in Fig.  8(a), the walker locates near the line x= – y, and appears at the position (0, 0) with the maximal probability. Whereas for the initial entangled state , the walker also remains near the line x= – y in Fig.  8(b), and the distribution along the line x= – y is similar to that of the 1D QW without phase disorder. We find that the line disorder passing through the original position (0, 0) has an apparent influence on the properties of the 2D QW, while the line disorder far away from (0, 0) has less impact.

Fig. 8. The distributions of 2D QW with line disorder eiϕ (ϕ =π ) at x=y for (a) the separated initial coin state (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2 and (b) the entangled initial coin state .

The variance of the 2D QW with line disorder at x=y is shown in Fig.  9. The variance of the 2D QW without line disorder is larger than that with the line disorder for the same n. The line disorder at x=y decelerates the spread velocity of the walker. For the separated initial coin state (|0⟩ +i |1⟩ )(|0⟩ +i |1⟩ )/2 ((|0⟩ – i |1⟩ )(|0⟩ – i |1⟩ )/2), the walker locates nearly along the line x= – y and P(0, 0) is the largest, while for the entangled initial coin state , the walker spreads along the line x= – y. Thus the variance of the 2D QW with line disorder at x=y with the initial separated coin state is smaller than that with the initial entangled coin state for the same n, as shown in Fig.  9.

Fig. 9. The variance of 2D QW with line disorder eiϕ (ϕ =π ) at x=y for different initial coin states.

4. 2D QW with circle disorder in phase

In this section, we study the features of the 2D QW with circle disorder in phase. The unitary operator of the 2D QW with the phase disorder at circle x2+y2=r2 is

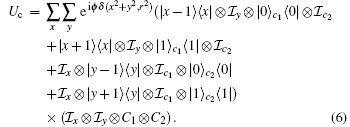The distribution of the 2D QW with circle disorder at x2+y2=4 exhibits localization for both the separated coin state |00⟩ and the entangled coin state , as shown in Figs.  10(a) and 10(b). There also exists localization in the 2D QW with circle disorder at x2+y2=2 for both the separated initial coin state and the entangled initial coin state. However, the localization cannot be observed in the 2D QW with circle disorder if the radius of the circle is increased to r> 2. This is because the overlap between the initial state and the localized stationary states of the unitary operator for the 2D QW with circle disorder atx2+y2=r2 equals 0 when r> 2. We also find that the 2D QW with circle disorder whose center is not at (0, 0) does not exhibit localization for any initial state. For the 2D QW with circle disorder atx2+y2=4 and the initial separated state |00⟩ , F=0.6300. For the entangled initial coin state , F=0.7330. When the circle disorder is added at x2+y2=2, for the initial coin state |00⟩ , F=0.2947, and for , F= 0.2618. Thus there is localization for the 2D QW with circle disorder at x2+y2=4 and x2+y2=2 with specific initial coin states as shown in Figs.  10(a)– 10(d).

Fig. 10. The distributions of 2D QW with circle disorder eiϕ (ϕ =π ) at (a) x2+y2=4 for the separated initial coin state |00⟩ ; (b) x2+y2=4 for the entangled initial coin state ; (c) x2+y2=2 for the separated initial coin state |00⟩ ; (d) x2+y2=2 for the entangled initial coin state .

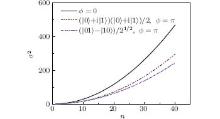
The 2D QW with circle disorder at x2+y2=4 and x2+y2=2 has localization, and the walker’ s spread velocity is decreased. Thus the variance of the 2D QW with circle disorder is smaller than that of the 2D QW without disorder for the same n, as shown in Fig.  11.

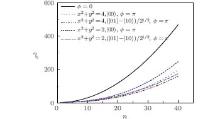Fig. 11. The variance of 2D QW with circle disorder eiϕ (ϕ =π ) as a function of the evolution time n.

5. Conclusion

We have shown the features of the 2D QW with point, line, and circle disorders in phase eiϕ (ϕ =π ) via the position distribution and the variance. A localization can be observed with certain phase disorder and specific initial coin states, and can be explained through the overlap between the initial state and the localized stationary states of the unitary operator of the whole system. In future work, it would be interesting and useful to discuss the influence of the position-dependent phase disorder on the 2D QW, which can be used to study quantum resonance and chaos.

Reference
1 Aharonov Y, Davidovich Y L and Zagury N 1993 Phys. Rev. A 48 1687 DOI:10.1103/PhysRevA.48.1687 [Cited within:1] [JCR: 3.042]
2 Guillotin-Plantard N and Schott R 2006 Dynamic Rand om Walks: Theory and Application Amsterdam Elsevier [Cited within:1]
3 Xue P 2013 The Journal of Computational and Theoretical Nanoscience: Special Issue: Theoretical and Mathematical Aspects of the Discrete Time Quantum Walk 10 1 [Cited within:1]
4 Qin H and Xue P 2014 Chin. Phys. B 23 010301 DOI:10.1088/1674-1056/23/1/010301 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
5 Xue P and Sand ers B C 2012 Phys. Rev. A 85 022307 DOI:10.1103/PhysRevA.85.022307 [Cited within:1] [JCR: 3.042]
6 Ambainis A 2003 International Journal of Quantum Information 1 507 DOI:10.1142/S0219749903000383 [Cited within:1] [JCR: 0.918]
7 Childs A M, Cleve R, Deotto E, Farhi E, Gutmann S and Spielman D A 2003 Proc. rm 35th ACM Symposium on Theory of Computing (STOC) 59 68 DOI:10.1145/780542.780552 [Cited within:1]
8 Shenvi N, Kempe J and Whaley K B 2002 Phys. Rev. A 67 052307 DOI:10.1103/PhysRevA.67.052307 [Cited within:1] [JCR: 3.042]
9 Wu J J, Zhang B D, Tang Y H, Qiang X G and Wang H Q 2013 Chin. Phys. B 22 050304 DOI:10.1088/1674-1056/22/5/050304 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
10 Oliveira A C, Portugal R and Donangelo R 2006 Phys. Rev. A 74 012312 DOI:10.1103/PhysRevA.74.012312 [Cited within:1] [JCR: 3.042]
11 Ahlbrecht A, Alberti A, Meschede D, Scholz V B, Werner A H and Werner R F 2012 New J. Phys. 14 073050 DOI:10.1088/1367-2630/14/7/073050 [Cited within:1] [JCR: 4.063]
12 Brun T A, Carteret H A and Ambainis A 2003 Phys. Rev. Lett. 91 130602 DOI:10.1103/PhysRevLett.91.130602 [Cited within:1] [JCR: 7.943]
13 Crespi A, Osellame R, Ramponi R, Giovannetti V, Fazio R, Sansoni L, Nicol F D, Sciarrino F and Mataloni P 2013 Nat. Photon. 7 322 DOI:10.1038/nphoton.2013.26 [Cited within:1] [JCR: 27.254]
14 Wójcik A, Luczak T, Kurzyński P, Grudka A, Gdala T and Bzdega M B 2012 Phys. Rev. A 85 012329 DOI:10.1103/PhysRevA.85.012329 [Cited within:1] [JCR: 3.042]
15 Zhang R, Xue P and Twamley J 2014 Phys. Rev. A 89 042317 DOI:10.1103/PhysRevA.89.042317 [Cited within:1] [JCR: 3.042]
16 Kitagawa T, Rudner M S, Berg E and Demler E 2010 Phys. Rev. A 82 033429 DOI:10.1103/PhysRevA.82.033429 [Cited within:1] [JCR: 3.042]
17 Kitagawa T, Broome M A, Fedrizzi A, Rudner M S, Berg E, Kassal I, Aspuru-Guzik A, E. Demler E and White A G 2012 Nat. Commun. 3 882 DOI:10.1038/ncomms1872 [Cited within:1] [JCR: 10.015]
18 Zhan X, Qin H, Bian Z H, Li J and Xue P 2014 Phys. Rev. A 90 012331 DOI:10.1103/PhysRevA.90.012331 [Cited within:2] [JCR: 3.042]
19 Xue P and Sand ers B C 2014 Phys. Rev. A 90 012331 DOI:10.1103/PhysRevA.90.012331 [Cited within:1] [JCR: 3.042]
20 Xue P and Sand ers B C 2012 Phys. Rev. A 85 022307 DOI:10.1103/PhysRevA.85.022307 [Cited within:1] [JCR: 3.042]
21 Childs A M 2009 Phys. Rev. Lett. 102 180501 DOI:10.1103/PhysRevLett.102.180501 [Cited within:1] [JCR: 7.943]
22 Childs A M, Gosset D and Webb Z 2013 Science 339 791 DOI:10.1126/science.1229957 [Cited within:1]
23 Lovett N B, Cooper S, Everitt M, Trevers M and Kendon V 2010 Phys. Rev. A 81 042330 DOI:10.1103/PhysRevA.81.042330 [Cited within:1] [JCR: 3.042]
24 Kendon V and Maloyer O 2007 Theoretical Computer Science 394 187 [Cited within:1] [JCR: 0.489]
25 Tang B, Qin H, Zhang R, Liu J M and Xue P 2014 Chin. Phys. B 23 050307 DOI:10.1088/1674-1056/23/5/050307 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
26 Xue P 2012 Chin. Phys. B 21 010308 DOI:10.1088/1674-1056/21/1/010308 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
27 Xue P 2012 Chin. Phys. B 21 100306 DOI:10.1088/1674-1056/21/10/100306 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
28 Xue P 2011 Chin. Phys. B 20 100310 DOI:10.1088/1674-1056/20/10/100310 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
29 Kurzyński P and Wójcik A 2011 Phys. Rev. A 83 062315 DOI:10.1103/PhysRevA.83.062315 [Cited within:1] [JCR: 3.042]
30 Broome M A, Fedrizzi A, Lanyon B P, Kassal I, Guzik A A and White A G 2010 Phys. Rev. Lett. 104 153602 DOI:10.1103/PhysRevLett.104.153602 [Cited within:1] [JCR: 7.943]
31 Kitagawa T, Broome M A, Fedrizzi A, Rudner M S, Berg E, Kassal I, Aspuru-Guzik A, Demler E and White A G 2012 Nat. Commun. 3 882 DOI:10.1038/ncomms1872 [Cited within:1] [JCR: 10.015]
32 Schreiber A, Cassemiro K N, Potoček V, Gábris A, Mosley P J, Andersson E, Jex I and Silberhorn Ch 2010 Phys. Rev. Lett. 104 050502 DOI:10.1103/PhysRevLett.104.050502 [Cited within:1] [JCR: 7.943]
33 Schreiber A, Cassemiro K N, Potoček V, Gábris A, Jex I and Silberhorn Ch 2011 Phys. Rev. Lett. 106 180403 DOI:10.1103/PhysRevLett.106.180403 [Cited within:1] [JCR: 7.943]
34 Peruzzo A, Lobino M, Matthews J C F, N. Matsuda N, Politi A, K. Poulios K, Zhou X, Lahini Y, Ismail N, Wörhoff K, Bromberg Y, Silberberg Y, Thompson M G and OBrien J L 2010 Science 329 1500 DOI:10.1126/science.1193515 [Cited within:1]
35 Schreiber A, Gábris A, Rohde P P, Laiho K, štefan̈ák M, Potoček V, Hamilton C, Jex I and Silberhorn Ch 2012 Science 336 55 DOI:10.1126/science.1218448 [Cited within:1]
36 Crespi A, Osellame R, Ramponi R, Giovannetti V, Fazio R, Sansoni L, Nicola F D, Sciarrino F and Mataloni P 2013 Nat. Photon. 7 322 DOI:10.1038/nphoton.2013.26 [Cited within:1] [JCR: 27.254]
37 Xue P, Qin H, Tang B and Sand ers B C 2014 New J. Phys. 16 053009 DOI:10.1088/PhysRevLett.16.053009 [Cited within:1] [JCR: 4.063]
38 Xue P, Qin H and Tang B 2014 Scientific Reports 4 4825 DOI:10.1038/srep04825 [Cited within:1]
39 Xue P, Qin H, Tang B, Zhan X, Bian Z H and Li J 2014 Chin. Phys. B 23 110307 DOI:10.1088/PhysRevLett.23.110307 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
40 Du J, Li H, Xu X, Shi M, Wu J, Zhou X and Han R 2003 Phys. Rev. A 67 042316 DOI:10.1103/PhysRevA.67.042316 [Cited within:1] [JCR: 3.042]
41 Ryan C A, Laforest M, Boileau J C and Laflamme R 2005 Phys. Rev. A 72 062317 DOI:10.1103/PhysRevA.72.062317 [Cited within:1] [JCR: 3.042]
42 Lu D, Zhu J, Zou P, Peng X, Yu Y, Zhang S, Chen Q and Du J 2010 Phys. Rev. A 81 022308 DOI:10.1103/PhysRevA.81.022308 [Cited within:1] [JCR: 3.042]
43 Cote R, Russell A, Eyler E E and Gould P L 2006 New J. Phys. 8 156 DOI:10.1088/1367-2630/8/8/156 [Cited within:1] [JCR: 4.063]
44 Karski M, Förster L, Choi J, Steffen A, Alt W, Meschede D and Widera A 2009 Science 325 5937 [Cited within:1]
45 Zähringer F, Kirchmair G, Gerritsma R, Solano E, Blatt R and Roos C F 2010 Phys. Rev. Lett. 104 100503 DOI:10.1103/PhysRevLett.104.100503 [Cited within:1] [JCR: 7.943]
46 Schmitz H, Matjeschk R, Schneider Ch, Glueckert J, Enderlein M, Huber T and Schaetz T 2009 Phys. Rev. Lett. 103 090504 DOI:10.1103/PhysRevLett.103.090504 [Cited within:1] [JCR: 7.943]
47 Xue P and Sand ers B C 2008 New J. Phys. 8 053025 [Cited within:1] [JCR: 4.063]
48 Xue P and Sand ers B C 2013 Phys. Rev. A 87 022334 DOI:10.1103/PhysRevA.87.022334 [Cited within:1] [JCR: 3.042]
49 Xue P and Sand ers B C 2009 Phys. Rev. Lett. 103 183602 DOI:10.1103/PhysRevLett.103.183602 [Cited within:1] [JCR: 7.943]
50 Kendon V and Tregenna B 2003 Phys. Rev. A 67 042315 DOI:10.1103/PhysRevA.67.042315 [Cited within:1] [JCR: 3.042]
51 Kendon V and Tregenna B 2004 Lect. Notes Phys. 633 253 DOI:10.1007/b13745 [Cited within:1]
52 Wójcik A Luczak T, Kurzynski P, Grudka A, Gdala T and Bednarska-Bzdega M 2012 Phys. Rev. A 85 012329 DOI:10.1103/PhysRevA.85.012329 [Cited within:1] [JCR: 3.042]
53 Segawa E 2013 Journal of Computational and Theoretical Nanoscience: Special Issue: Theoretical and Mathematical Aspects of the Discrete Time Quantum Walk 10 1583 DOI:10.1166/jctn.2013.3092 [Cited within:1]
54 Segev M, Silberberg Y and Christodoulides D N 2013 Nat. Photon. 7 197 DOI:10.1038/nphoton.2013.30 [Cited within:1] [JCR: 27.254]
55 Li Z J, Izaac J A and Wang J B 2013 Phys. Rev. A 87 012314 DOI:10.1103/PhysRevA.87.012314 [Cited within:1] [JCR: 3.042]
56 Xue P and Zhang Y S 2013 Chin. Phys. B 22 070302 DOI:10.1088/1674-1056/22/7/070302 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
57 Zhang R, Qin H, Tang B and Xue P 2013 Chin. Phys. B 22 110312 DOI:10.1088/1674-1056/22/11/110312 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
58 Xu Y Y, Zhou F, Chen L, Xie Y, Xue P and Feng M 2012 Chin. Phys. B 21 040304 DOI:10.1088/1674-1056/21/4/040304 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]