Quantum key distribution (QKD) allows two parties, called Alice and Bob, to share a common string of secret keys even in the presence of an adversary, called Eve. Since the proposal in 1984, ^[1] there has been much significant progress towards its practical implementation.^{[2– 4]} In the QKD protocol, Alice and Bob can share the string of keys over quantum communication. However, there may exist some discrepancies between the shared keys due to the imperfect control of devices and the disturbance of environment, or the behavior of Eve. The error rate caused by these factors should be estimated because: (i) in order to fulfill the security requirements, the error rate needs to be estimated as an important reference for detecting the presence of Eve; (ii) in a practical QKD system, post-processing is inextricably needed to eliminate the discrepancies between the shared keys. The estimated error rate can be used to optimize the performance of post-processing, in particular at key reconciliation stage. Several methods for key reconciliation have been proposed, such as Cascade, ^[5] and LDPC.^{[6, 7]} In Cascade, the knowledge of error rate is helpful to set an optimal size of block length that significantly saves its time overhead in practice.^[8] In LDPC, the error rate can help choose an appropriate code rate which can improve the efficiency and achieve higher key throughput.

For the purpose of clarity, we first categorize the error rates in QKD. Assume Alice and Bob share n bits sifted key, there are three kinds of error rates involved.

: It is the estimated error rate of the n bits sifted keys and generally obtained before key reconciliation.

e_sift: It is the error rate of the n bits sifted keys. If there are n_e bits discrepant between Alice's and Bob's sifted keys, e_sift is n_e/n, where e_sift can be precisely obtained once Alice and Bob have completed key reconciliation, by comparing the keys after reconciliation with the keys before.

e_∞ : It is the asymptotic value of e_sift as the sifted keys' size n becomes infinite. However, because in the practical application the size of sifted keys is finite, e_sift is probably more or less deviated from e_∞ .

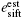
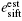
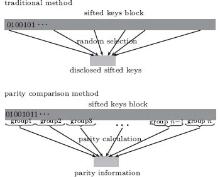
As a summary, is an estimation of e_sift, while e_sift is an estimation of e_∞ , e_sift needs to be estimated instantly in each reconciliation round for the purpose of good post-processing performance. In this paper the term “ error estimation” refers to the estimation of e_sift or in other words, the process of obtaining . We adopt the above notations throughout this paper.

In the traditional method of error estimation, the sampling of sifted keys is revealed directly from Alice to Bob or vice versa, which is around 10% – – 20% of sifted keys' size in general.^{[9– 11]} Then they can determine the by comparing the sampling keys. However, this method cannot produce a completely accurate result when the size of sifted keys is not big, say several kbits, which is a common situation in some reconciliation protocol. For example, in the reconciliation protocol using short-length LDPC codes, the sifted keys are arranged into blocks of several-thousand bits depending on the optimal code rate. Increasing the amount of sampling is one solution for achieving higher accuracy, but that simultaneously means more waste of sifted keys. In a practical QKD system, the generation speed of sifted keys can be as high as only around 3 Mbits per second at the distance of 20 km, ^[12] because of which sifted keys are precious and should be reconciled with disclosure as little as possible.

In this paper, an efficient error estimation method based on parity comparison is proposed, which shows good property both at short and long key sizes. First we elaborate on how the proposed method works. Then several simulations related are conducted, for investigating the performance of the proposed method.

In this section, the parity comparison method (PCM) is discussed with a schematic diagram. The traditional method (TM) and the PCM are drawn in Fig.  1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The schematics of two methods. In the traditional method, the sent message (the disclosed sifted keys) is randomly chosen from the sifted keys. In the PCM method, the sent message (parity information) is calculated group by group from the sifted keys.

In the TM, a sample of the sifted keys is randomly selected and revealed, through which Alice and Bob can get an error rate e_sample, which is then taken to be 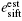directly. In contrast, in the PCM, the sifted keys are divided into groups, and the parity bit of each group is calculated

where b_i, b_parity ∈ {0, 1}. Then all the parity bits are revealed and compared between Alice and Bob. They can obtain the error rate of the parity bits: e_parity. However, e_parity will not be considered as 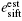directly. should be retrieved according to the following lemma.^[13]

Lemma Let Alice and Bob share a string of L sifted key bits. The probability for each corresponding bit in Alice's string and Bob's string to be different is e_sift and independently and identically distributed. Then the probability that Alice and Bob have different parities of the string is

Proof Alice and Bob have different parities of the string when there is an odd number of wrong bits in Bob's string relative to Alice's. Thus the probability can be expressed as

To prove that equation  (2) is equivalent to Eq.  (3), we just simply rewrite the right-hand side of Eq.  (2) as

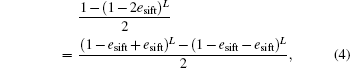and expand it in binomial series, which will obviously lead to Eq.  (3).

It is easily deduced that an odd number of wrong bits in a group in the PCM will lead to a wrong b_parity. Let the group size be L as in the lemma. The relation e_parity = p_odd is clear. Thus our goal is to obtain e_sift with e_parity through the above lemma. However, equation  (2) is difficult to solve backwards. It needs to be done in another way. Actually, a look-up table of Eq.  (2) can adequately accomplish the task. We can in advance store the e_parity values with respect to all e_sift values. The e_sift can be thus easily retrieved. In practice, once the e_parity is acquired, the corresponding in the table which gives the nearest to e_parity is thought to be . The table can be made with arbitrary accuracy.

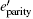
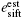
A rough security analysis is given here. Let N be the size of sifted keys. In the TM, if the ratio of sampling is α , the amount of leaked information of the sifted keys to Eve can be taken to be α N. In the PCM, if the size of a group is n, the amount of leaked information to Eve can be taken to be N/n. Thus, under the condition α = 1/n, the security levels of the two methods are identical.

For evaluating the estimation method, we need to investigate its average deviation from the real value. The average deviation is . The simulation of Δ for the TM and PCM is given in Fig.  2. The simulation is conducted with the sifted key size being 5000 bits and the result is averaged over 3000 times of simulations. In the TM, the sample ratio is 1/10, while in the PCM the group size is 15. From the previous section, it is known that the PCM leaks less information than the TM.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Simulation results of the PCM and TM. The sifted keys′ length for simulation is 5000 bits. The two lines illustrate the deviations of the two methods averaged over 3000 times. PCM outperforms the TM when the error rate is not very high, less than 6% .

It can be seen that although with less information leakage, the PCM still outperforms the TM in the error region less than around 6% . The improvement is defined as

As shown in Fig.  2, a 50% improvement at around e_sift = 3% is achieved. When it is higher than 6% , the PCM is less accurate than TM. However, this inaccuracy at high error rate does not influence PCM's practicability substantially, because nowadays the QKD system is typically running under an error rate of less than 3% , ^{[12, 14]} and what is more, few keys are generated when the system is running under an error rate higher than 6% . For the above reasons, the PCM is of much better practicability at short key sizes such as several kbits.

The above simulation uses a short key size of 5000 bits for error estimation, which is often needed when adopting LDPC as the error reconciliation method. However, if the reconciliation is not carried out by LDPC, for example Cascade, or if the error estimation is to only serve for a security parameter, the length of the string should be long enough, typically 1 Mbits, in order to eliminate the finite-size effect. Here we study the performance of the two methods when the sifted keys' length increases from 5000 bits to 1 Mbits. Recall that in Fig.  2 the two lines intersect at around 6% , which means the TM outperforms the PCM at this error rate. In other words, the intersection is the maximum error rate that the PCM is better than the TM. Therefore we can investigate the intersection at different sizes of sifted keys, which can indicate the tendency of accuracy shift of the two methods.

Figure  3 clearly shows that the TM outperforms the PCM at a smaller and smaller error rate as the sifted keys' block length grows, which means that the PCM is less and less advantageous. However, this does not destroy PCM's advantage over the TM, because the QKD system nowadays often runs at an error rate lower than 3% and what is more, in the reconciliation based on LDPC, the code length needed for error estimation or error correction is normally less than 1 Mbit.^{[15, 16]} So the PCM still has the advantage over the TM in the realistic situation.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Simulation results of the shift of the intersection of the PCM and TM. It indicates that the intersection point decreases as the length grows, which means that the PCM becomes less and less advantageous.

Finally, we investigate the effect of different group sizes on the PCM. The group size changes from 5 to 30 while the sifted key length is fixed at 1 Mbits. The sample ratio of the TM is fixed at 1/10. Similar to the previous simulation, we study the position of the intersection.

Figure  4 shows that as the group size increases, the intersection becomes smaller and smaller. This is reasonable because as mentioned above, a bigger group size corresponds to smaller disclosure. However, it is easily understood that to achieve a higher accuracy more information needs to be disclosed. Therefore bigger group size shows worse performance. Nevertheless, it can be seen that the PCM can still outperform the TM in the error rate region smaller than 2% even when the group size is 30, corresponding to 1/3 of the disclosed amount of the TM, which is very economic. Thus PCM is very meaningful and practical in real situations.

Fig. 4.

	Figure Option '>ViewDownloadNew Window
'>	Fig. 4. The position of intersections when the group size of PCM changes while the sample ratio of the TM is fixed at 1/10. The sifted keys' length is fixed at 1 Mbit.

We propose a simple but efficient method, called PCM, of key reconciliation for QKD. The PCM can outperform the TM in most realistic scenarios. Furthermore, the PCM can meet the same accuracy level with much less information leakage about the sifted keys, saving more sifted keys for generating secure keys. It should be emphasized that the is not used for privacy amplification. It is e_∞ that should substitute the error rate in the security analysis and final key generation.^[17] Once Alice and Bob have finished reconciling their keys, they can accurately get the e_sift as stated in the introduction section. Based on enough e_sift, a good estimated e_∞ can be achieved.