†Corresponding author. E-mail: lfxuphy@jlu.edu.cn
‡Corresponding author. E-mail:shihl@itp.ac.cn
*Project supported by the National Basic Research Program of China (Grant No. 2013CB834100), the National Natural Science Foundation of China (Grant Nos. 11121403 and 11274320), the Open Project Program of State Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, China (Grant No. Y4KF171CJ1), the National Natural Science Foundation for Young Scholar of China (Grant No. 11304115), and the China Postdoctoral Science Foundation (Grant No. 2013M541282).
Small RNA(sRNA)-mediated post-transcriptional regulation differs from protein-mediated regulation. Through base-pairing, sRNA can regulate the target mRNA in a catalytic or stoichiometric manner. Some theoretical models were built for comparison of the protein-mediated and sRNA-mediated modes in the steady-state behaviors and noise properties. Many experiments demonstrated that a single sRNA can regulate several mRNAs, which causes crosstalk between the targets. Here, we focus on some models in which two target mRNAs are silenced by the same sRNA to discuss their crosstalk features. Additionally, the sequence-function relationship of sRNA and its role in the kinetic process of base-pairing have been highlighted in model building.
In bacteria, small RNAs (sRNA) post-transcriptionally regulate target mRNAs through base-pairing, which plays an important role in physiological processes, such as iron metabolism, [1] acid stress, [2] quorum sensing, [3] and outer membrane protein expression.[4] sRNA have been categorized into two types according to the location in the genome: cis-encoded sRNA and trans-encoded sRNA. The former is located in the same region as its target mRNA in the genome and completely bases pairing with the target, while the latter is located in regions different from those of its targets and partially bases pairs with the targets.[5] Here, we focused on trans-encoded sRNAs, which usually have three basic regions: the core interaction region, the Hfq-binding site, and a rho-independent terminal. The core interaction region, also called the “ seed ” region, helps sRNA to specifically discern target mRNAs and initiates the base-pairing with mRNAs.[6] The Hfq-binding site usually an AU-rich region, helps sRNA bind at the proximal face of Hfq.[7] Hfq is a donut-shaped homohexamer that facilitates the base-pairing of sRNA and mRNA through improving sRNA stabilization or structural transformation of mRNA.[8, 9] However, the exact mechanism underlying the effect of Hfq is not clear. Recently, some experiments have revealed that polyU of the terminal of sRNA is another Hfq-binding site and is necessary for the efficacy of sRNA.[10, 11] sRNA has two effects on the translation of mRNA: negative regulation, in which sRNA base pairing with mRNA near the ribosome binding site (RBS) inhibits the loading of ribosomes, and thus the translation of mRNA is repressed, [12, 13] and active regulation, [14– 16] in which the binding of sRNA loosens the intra-base-pairing of RBS of mRNA so that the ribosome can carry out the translation. In the scenario of negative regulation, most of the sRNA-mRNA duplex is stoichiometrically degraded by endonuclease.[17] Various models of sRNA-mediated regulation are shown in Fig. 1.
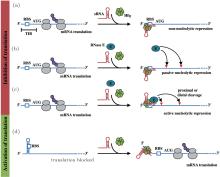 | Fig. 1. Small RNA-based regulatory mechanisms of mRNA expression. (a) sRNA blocks translation of mRNA by directly binding to the ribosome binding site (RBS) of mRNA. (b) and (c) The binding of sRNA on mRNA sequesters the ribosome, because of which endonuclease sites are exposed to degradation by RNase E in a passive or active manner. (d) The RBS region of mRNA shows intra-base-pairing in the absence of sRNA that inhibits translation of mRNA. The binding of sRNA loosens the RBS so that it is available in a form of a single strand for translation by the ribosome. The grey ovals indicate the ribosomes that are involved in the translation of mRNA. The purple circles indicate the proteins generated. AUG is the start codon for translation of mRNA.[17] |
Recently, another model has demonstrated that ChiX (MicM) sRNA catalytically regulates chip (ybfM) mRNA, which indicates that sRNA does not undergo codegradation with mRNA in a stoichiometric manner but with recycling.[18, 19] Based on the results of these experiments, Hao et al. built a catalytic-sRNA-mediated gene silencing (CSMGS) model to analyze its novel properties.[20] For trans-encoded sRNAs, they usually regulated several mRNAs that comprise a network, [21, 22] such as ChiX sRNA which is also codegraded with another target chbB mRNA, and is exhausted in a stoichiometric model to release chiP mRNA.[19, 23]
With the accumulation of experimental data, several models have been built to characterize the regulatory system. In this review, first, we have presented an sRNA-mediated regulatory model in a stoichiometric manner, [24] and compared it with the protein-mediated post-transcription model. Second, we have discussed the features of the catalytic model and stoichiometric model with respect to sRNA-mediated regulation from both steady-state analysis and noise analysis. Third, we have introduced a model depicting the simplest network of two target mRNAs regulated by a single sRNA, which shows the hierarchical crosstalk behavior between the target mRNAs. Fourth, we have discussed the latest research on the sequence-function relationship of sRNA in gene silencing, which should provide the foundation and basis of modeling the sRNA-mediated regulation.
sRNAs post-transcriptionally regulated the expression of mRANs, which differs from the transcriptional regulation of transcription factors (TFs), a kind of protein-mediated regulation. Levine et al. found that sRNA-mediated regulation exhibited novel properties, such as the threshold-linear property and that it more tightly repressed target mRNA below the threshold and showed better robust noise resistance than protein-mediated regulation. [24] For further discussion of the characteristics, we introduce the work of Mehta et al.; they treated TF-mediated and sRNA-mediated regulation as a signal-processing system and accordingly discussed the steady-state behavior, noise properties, frequency-dependent gain, and dynamical response to the input signals.[25]
Mehta et al. built a model for sRNA-mediated regulation by using mass action equations combined with intrinsic noise defined by Langevin terms as fellows:
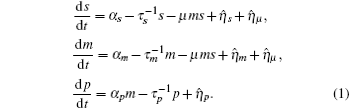
In this model, the sRNA (mRNA) transcription rate is set as α s (α m), and degradation rate is set as 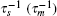
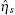
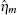

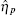

The TF-mediated transcriptional regulation is modeled using the Langevin equations:[26– 29]
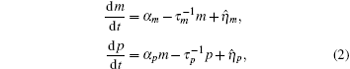
where 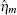
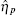
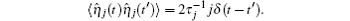
Ignoring the Langevin terms and setting the derivatives to zero in Eqs. (1) and (2), we can determine the amount of proteins in the steady state in both sRNA-mediated and TF-mediated regulation. Consistent with the study of Levine et al., sRNA-mediated regulation shows the linear-threshold property for the target mRNA expression level with the threshold around α m ∼ α s. [24] When α m ≤ α s, the translation of mRNA is repressed; when α m ≫ α s, the expression level of protein is linear to (α m – α s). The binding strength μ just determines the smoothness of the crossover around the threshold α s. By contrast, the amount of mRNA in the TF-regulated steady state is a linear function of α m.[26– 29]
Based on the equations above, they also studied the intrinsic noise properties, [30– 32] frequency-dependent gain (amplification), [33] and dynamical response to large input signals of sRNA-mediated and protein-mediated regulation.[34] Taken together, their characteristics are summarized in Table 1 cited from Mehta et al.[25]
| Table 1. Summary of the advantages and disadvantages of sRNAs as compared with transcriptional protein regulators (transcription factors). |
sRNA-mediated gene silencing was initially believed to occur in the stoichiometric mode, which differs from the protein-mediated catalytic mode. However, some experiments in bacteria showed that sRNA can exert its effects in the catalytic mode also, which means that sRNA can promote the degradation of mRNA with a certain ratio of sRNA survival.[18, 19]
To investigate the characteristics of sRNA-mediated regulation with recycling, Hao et al. developed the catalytic-sRNA-mediated gene silencing model (CSMGS), [20] based on Levine’ s model (Fig. 2).[24] They introduced the recycling rate δ referring to how much sRNA is surviving from the sRNA-mRNA combo degradation. The resulting recycling item δ β sm(s– m) was added in the catalytic model shown in Eqs. (3), in which β sm(s– m) means the degradation rate of sRNA-mRNA combo. Therefore, setting δ to 0 transforms the catalytic model into the stoichiometric model. As mentioned above, Hfq is necessary for most of the trans-encoded sRNA regulation, but the mechanism is not very clear. Here both models assumed that Hfq is abundant.[35]
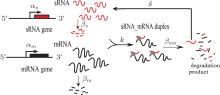 | Fig. 2. Catalytic-sRNA-mediated gene silencing (CSMGS) model.[20] |
The mass action equations of CSMGS model are
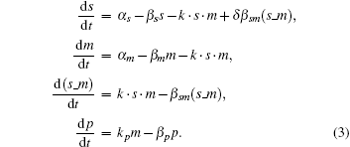
In this model, s (m), α s (α m), and β s (β m) indicate the sRNA (mRNA) concentration, the transcription rate, and the degradation rate, respectively. The binding rate k refers to the strength of sRNA-mRNA interaction which is relevant to the kinetic process of base-pairing of sRNA with mRNA.
Setting the differential equations to zero yields
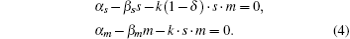
When 0 ⩽ δ < 1, the stationary solution of sRNA, mRNA, sRNA-mRNA duplex, and protein can be obtained as follows:
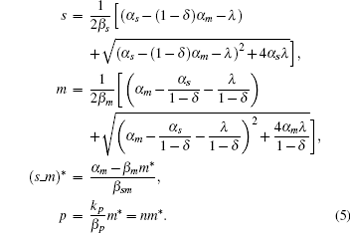
The parameter λ is defined as λ = β m β s/k, which indicates the ratio of the spontaneous and codegradation rates. n = kp/β p refers to the burst size of target protein production. Some experiments have suggested that the base-pairing of sRNA with mRNA is strong and fast; therefore, we can approximate λ to zero.[20] Then the stationary solution of mRNA can be written as follows:
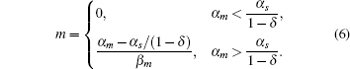
Figure 3(a) shows the steady-state expression level of mRNA responding to its transcription rate for different recycling ratios of sRNA. In the case of δ = 0, the CSMGS model refers to the stoichiometrical regulation mode of sRNA, whose threshold-linear property has been discussed in the model of Levine et al.[24] The CSMGS model exhibited the similar threshold-linear property, but with the threshold characterized by α s/(1 − δ ). When the transcription rate of mRNA crosses the threshold, the amount of mRNA is linearly related to α m. Compared to the stoichiometric mode, in the catalytic mode, gene silencing by sRNA is more rapid because a lesser number of sRNA are required to degrade mRNA with a given α m.[20, 36]
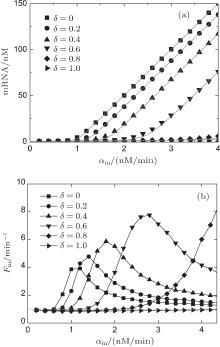 | Fig. 3. Stationary solutions and Fano factors of target mRNA vary with its transcription rate α m in different recycling ratio in the CSMGS model.[20] |
It is believed that noise significantly affects the dynamics behavior of molecules in vivo such as sRNAs, mRNAs and proteins.[37, 38] There are mainly two types of noise: intrinsic noise, which is related to the low reactant number and reactant stochastic bursting, [38– 40] and output noise, which is related to diffusion between reactant pools and the neighboring environment.[41] Here we focus on the intrinsic noise in sRNA-mediated gene silencing.
Generally, there are three approaches to study the noise of the biochemical reactions. The first approach is by means of Langevin equations (as in Eq. (1)), [42] which was further developed as the linear noise approximation (LNA).[39, 43] This method can provide analytical results for both the mean value and variance of each reactant. The second approach is to use the master equation.[38, 44] All biochemical reactions can be depicted in the master equation, which gives the evolution of the joint probability of all the reactant species. Generally, it is difficult to solve the master equation analytically; therefore, many researchers will choose the third approach of stochastic simulation with the Gillespie algorithm.[45– 47]
One can choose the appropriate strategy according to the research objective; all these objectives can provide the mean value x̅ and variances 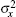
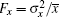
In previous studies, it was believed that the transcription of RNA is a standard Poisson process, which means that the Fano factor Fs = Fm = 1.[38, 39] However, the sRNA-mediated gene silencing is not a pure Poisson process. Only when the parameter α m is far away from the regulatory threshold, the Fano factor is close to 1, while the Fano factor around the threshold is much larger than 1 (Fig. 3(b)). The burst of the noise of target mRNA around the threshold is due to the anticorrelation between the number of mRNAs and that of sRNAs.[48] This conclusion can be fit to both Levine et al.’ s model and the CSMGS model.
Comparison of the noise properties of the two models suggested that the catalytic sRNA can more strictly repress the target mRNA at the threshold site of α m ∼ α s.[20, 46] Figure 3(b) exhibits a right-shift threshold of the noise amplification effect for the CSMGS.
Another important question that arises pertains to the noise transmitted in the process of sRNA-mediated gene regulation, for example, whether the noise at the mRNA level would be transmitted to the protein level. Therefore, in the scenario of sRNA, the noise strength of protein expression includes the bursting noise of the mRNA and protein production.[20] However, for protein-mediated regulation, the noise is calculated by Fp ≈ 1 + n.[26, 39, 44]
Many trans-encoded sRNAs target several mRNAs, and a single mRNA can also be regulated by different sRNAs, which form a complex network.[6, 34, 49] In the case of multiple mRNAs repressed by a single sRNA, mRNAs will crosstalk with each other through sRNA competition.[50] Considering some cases of double-target mRNAs, sRNA may regulate both mRNAs in the stoichiometric mode, for example, RyhB undergoes codegradation with sodB and sdhCDAB mRNA; [1] however, in some other cases, sRNA can catalytically regulate one mRNA, while stoichiometrically regulating the other mRNA, for example ChiX represses chiP and chbB.[18, 19]
Levine et al. extended the kinetic model (Eq. (3)) into a two-target mRNAs model and found that mRNAs exhibit hierarchical cross-talk that is determined by the binding rate k.[24] When the reporter mRNA binds with sRNA more strongly than another mRNA (kR > kT), the reporter mRNA can exhaust the sRNA pool quickly and release the repression of the later target mRNA, the function of which is similar to the “ switch effect” .[24, 51]
The CSMGS model has been taken in discussing the crosstalk of two mRNAs by setting of one of the mRNAs regulated in the catalytic mode and the other in the stoichiometric mode.[51] In the completely catalytic model, as δ = 1, the crosstalk is one-directional. The mRNA in the stoichiometric mode exhausts sRNA to “ switch on” the mRNA in the catalytic mode. This has been experimentally demonstrated in the ChiX– chiP– chb system.[18, 19] Before adequate induction, chb as a target mRNA is repressed by ChiX through base-pairing. On growth in chitobiose medium, the chb operon is induced. Along with the increase in chb, chb mRNA transforms from target mRNA completely repressed by ChiX sRNA to “ trap-mRNA” , which causes the degradation of ChiX. When the amount of chb mRNA exceeds that of ChiX, signifying across the threshold depicted by Levine et al., the translation of chiP mRNA is released.[18– 20, 24]
Based on the noise study of the single-target model, researchers have provided a new noise profile for two target mRNAs competing to exhaust the same sRNA pool. Same as the single target model, of which the noise around the threshold (α m ≃ α s) tends to be amplified, the noise of the two-targets model also presents a series of peaks in the crossover region ((α m1 + α m1) ≃ α s).[51] This remarkable feature can be used in experiments to explore the crosstalk of double targets mediated by sRNA.
Recently, there has been further novel progress in the multi-targets model where the target number is far greater than two.[47, 50] Bosia et al. found that one target mRNA above its regulatory threshold is able to drive other common target crossover thresholds, and that hierarchical crosstalk among the multiple targets is much more notable.[47] Jost et al. proposed that sRNA weakly regulates many mRNAs as auxiliary targets, which have no effect on the phenotype of the organism but provide a buffer to confer robustness to few “ principal” targets.[50] These developments have improved the understanding of sRNA-mediated gene regulation.
sRNA-mediated regulation is dependent on base-pairing with mRNA; therefore the functional efficiency of sRNA should be determined by the kinetic process of base-pairing. Some experiments highlighted the factors working on sRNA-mediated regulation, such as the length of the core interaction region, the secondary structure and the duplex formation energy.[20, 52] The factors and the relevant energies could be used in the algorithms for searching the latent sRNA-mRNA system in vivo and were also modeled to artificially synthesize the sRNA-mRNA system.[53– 55] Therefore, here we introduced some work involving quantification of the sequence-function relationship in sRNA-mediated regulation to discern the primary factors.
Hao et al. constructed a series of mutants of RyhB and sodB, especially the complementary mutants in the core interaction region, and suggested that fold-repression is exponentially correlated with the duplex energy Δ E in the case of no interruption in the core interaction region. They also found the energy related the secondary structure of the Hfq-binding region to be a good predictor for the efficacy of sRNA.[56] Further study suggested that the local secondary structure of sRNA may weaken the efficiency of sRNA owing to its unavailability in the kinetic process of base-pairing. According to the experimental results, an energetic term, Δ Eopen, was introduced to characterize the energy of opening of the local structure. We hypothesized that the competition between Δ Eopen and the base-pairing energy of the core interaction region determined the parameters kon and koff in the first step of the base-pairing process. Currently, the work is under preparation for submission.
Many studies have emphasized the importance of the successive base-pairing of the core interaction region, but Peterman et al. found that the loosened stem-loop structure harboring the core interaction region tolerates mismatch in the core interaction region to maintain the function of sRNA.[52] Peterman et al. signified the binding energy of the core interaction and the stability of the first and third stem-loop structures of RyhB. A two-state binding model was built to fit the experimental data, which assumed that the relative probability of an unbound state to the bound state is determined by the energy difference Δ E between the bound and unbound states.

In the heuristic model, the energy term can be written as
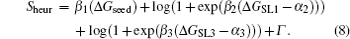
The first term depicts the binding energy of the core interaction region, and the second and third depict the stability of the stem-loop structures. The addictive parameters are combined into Γ .[32]
sRNA-mediated and protein-mediated regulations are important for bacteria to adapt to the environment. The two regulatory approaches have different features, and each of them has advantages and disadvantages, for example sRNA can rapidly respond to large changes in the input signal and shut down downstream expression, while protein-mediated regulation is better at transmitting small input signals for quantitative adjustment. It is known that, sRNA functions in diverse modes of activating or repressing the translation of mRNA, but there has been less theoretical study on active regulation. Here we focused on the models of sRNA-mediated gene silencing.
Two types of sRNA-mediated gene silencing have been demonstrated by mass equations: stoichiometric regulation, in which sRNA undergoes codegradation with mRNA, and catalytic regulation, in which partial sRNA codegradation of mRNA is recycled as free state sRNA. The catalytic model (CSMGS) inherits the linear-threshold property of the stoichiometric model, but presents stronger repression of the target mRNA, not only in inhibiting the mRNA expression but also in restricting its noise strength. Although both the models we introduced concern the scenarios of degradation of mRNA caused by sRNA, Equation (3) can also be used to depict another kind of sRNA-mediated gene silencing where it represses the translation without degradation of mRNA, which also exhibits the linear-threshold property.[24]
When multiple mRNAs are regulated by a single sRNA, they may affect the translation of each other through sRNA competition. The crosstalk of mRNAs exhibits hierarchy property, which means the sRNA shows regulation prioritization among multiple mRNAs. This property has been observed in different experiments and models.[24, 57] The theoretical model proposed that only strongly binding mRNA can efficiently release the repression of the weak binding mRNA regulated by the same sRNA, but the reverse is invalid. Therefore, the strong binding mRNA can be considered as a switch for the weakly binding mRNA in both stoichiometric and catalytic modes.
In the context of a single target, theoretical models demonstrated that the binding rate k of sRNA-mRNA interaction has no influence on the threshold value, but just determines the stiffness of the transition from repression to release.[20, 24] However, when multiple targets are expressed simultaneously, the relative binding rate contributes to the hierarchic crosstalk of mRNAs. In the last section of the paper, we have introduced some studies on the factors related to the efficacy of sRNA, most of which were believed to determine the binding rate of the kinetic process. Recently, Fei et al. applied single-molecular fluorescence in situ hybridization and single-molecular localization-based super-resolution microscopy to measure the numbers of sRNA, mRNA, and sRNA-mRNA complex, and then fitted them in the kinetic model to obtain kinetic parameters, which is the first time that the kinetic parameters in sRNA-mediated regulation have been measured in vivo. The results suggested that the base-pairing of SgrS sRNA with ptsG mRNA is a reversible process with a large dissociation constant.[58] This work inspired us to combine the measured kinetic parameters and secondary structures of sRNA to further study the kinetic process of base-pairing and the internal correlation, which will promote the development of the theoretical model.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|


