†Corresponding author. E-mail: syran@wzu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 21204065 and 20934004) and the Natural Science Foundation of Zhejiang Province, China (Grant No. Y4110357).
DNA condensation is an important process in many fields including life sciences, polymer physics, and applied technology. In the nucleus, DNA is condensed into chromosomes. In polymer physics, DNA is treated as a semi-flexible molecule and a polyelectrolyte. Many agents, including multi-valent cations, surfactants, and neutral poor solvents, can cause DNA condensation, also referred to as coil–globule transition. Moreover, DNA condensation has been used for extraction and gene delivery in applied technology. Many physical theories have been presented to elucidate the mechanism underlying DNA condensation, including the counterion correlation theory, the electrostatic zipper theory, and the hydration force theory. Recently several single-molecule studies have focused on DNA condensation, shedding new light on old concepts. In this document, the multi-field concepts and theories related to DNA condensation are introduced and clarified as well as the advances and considerations of single-molecule DNA condensation experiments are introduced.
DNA is the most important biomolecule and as such has always been of great interest. In a good solvent, DNA is macromolecule carrying negative charges and exists in a random coil conformation. However, within cells or viruses, DNA is organized into a chromosome (within the cell nucleus) or in a toroidal conformation (in the viral capsid). For the transcription process to occur, the condensed DNA must be unraveled to expose genomic information to functional proteins such as RNA polymerase.[1] From a physical point of view, long-chain DNA molecules can be treated as a semiflexible polymer and a polyelectrolyte. When condensing cationic ions are added, DNA binds to the ions and its charges are neutralized. When approximately 90% of the DNA charges are screened, the DNA can overcome intra- and inter-chain electrostatic repulsion and condensation occurs; addition of crowding polymers such as polyethylene glycol, together with screening salt ions, also leads to DNA condensation. This process is referred to as coil– globule transition or Ψ (psi, polymer- and salt-induced) condensation in polymer science.[2, 3] In the field of applied technology, DNA condensation is an important step in DNA extraction; in medical fields such as gene therapy, therapeutic DNA molecules are often condensed into particles carrying positive charges in order to overcome the electrostatic repulsion of the negatively charged cell membrane and steric hindrance (Fig. 1).[4]
Because of the importance of DNA condensation in biological processes, polymer physics, and the fields of applied technology, numerous experimental studies have sought to elucidate the morphologies of condensed DNA, the dynamics of condensation, and the effect of regulatory factors (such as salt concentration, temperature, etc.). Several physical theories explaining the mechanism of condensation have been presented. These studies have been summarized in several reviews, including earlier reviews written by Bloomfield[5, 6] as well as the more recent ones.[7– 13] However, since many concepts and terms are widely used in these reviews and research literature this may hinder the understanding of researchers from other fields. We believe that clarifying concepts is a key step in understanding a scientific issue. Moreover, recent single-molecule studies have provided new results and novel interpretations of old concepts, which were not discussed in previous reviews. Therefore, this paper aims to clarify the concepts, terms, and theories relating to DNA condensation and introduces single-molecule experiments shedding new light on old concepts.
The structure of this paper is as follows: (i) fundamental knowledge regarding DNA and the related concepts are clarified; (ii) DNA condensing agents, experimental techniques, and the morphologies of the condensed DNA are briefly presented; (iii) the paper focuses on various theories and concepts relating to DNA condensation; (iv) a number of single-molecule experimental advances are introduced.
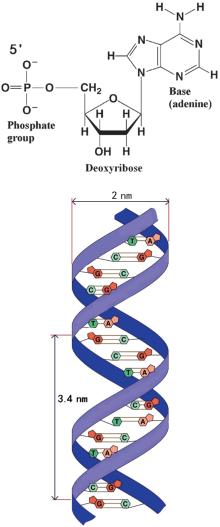
Most DNA (Deoxyribonucleic acid) molecules consist of two strands, which are coiled around each other to form a double helix. Both strands are composed of basic units called nucleotides. Each nucleotide is composed of three parts: a nucleobase [either guanine (G), adenine (A), thymine (T), or cytosine (C)], a deoxyribose, and a phosphate group (Fig. 2). The two strands are anti-parallel in direction; one backbone strand is termed the 3′ (three prime) and the other the 5′ (five prime). Hydrogen bonds are formed between the bases of the two separate polynucleotide strands according to the base pairing rules (A– T and G– C), thus forming the double-stranded DNA. The diameter of a typical B-DNA molecule is approximately 2 nm. A B-DNA helix cycle consists of 10 base pairs with a length of approximately 3.4 nm. DNA has the following physical characteristics: i) The backbone strands contain negative charges; each base pair consists of two negative charges, which means it is a polyelectrolyte. ii) DNA is rigid to a certain degree, but long-chain DNA is flexible enough over its persistent length scale. Therefore, it is considered to be a semiflexible macromolecule. In polymer physics, the Worm-Like-Chain (WLC) model can be used to describe the elastic behavior of such molecules.[14, 15] iii) Unlike normal macromolecules, DNA has a helical structure which leads to some unique behaviors such as supercoiling, denaturizing, and unzipping.
In the field of polymer science, DNA condensation is often defined as a transition process from the original coil conformation to the condensed conformation, which is also referred to as DNA collapse. The final condensed complex can be comprised of one or multiple DNA molecules. From an experimental point of view, the condensed complex in single-molecule experiments consists of one DNA molecule, whereas in other ensemble experiments, such as dynamic light scattering (DLS) and atomic force microscopy (AFM) methods, multiple DNA molecules are likely included in the final complex. In the field of biology, DNA condensation is also called DNA packaging (or folding), which results in the chromosome as a final product. The mechanism of DNA packaging remains to be clarified and many studies have focused on this issue.[16] In applied fields, DNA precipitation is a key process used in DNA extraction techniques. However, DNA condensation should be distinguished from DNA precipitation; the former is usually a necessary step of the latter, whereas the latter often involves additional processes including the aggregation of condensed particles and precipitation.
The addition of condensing agents above a critical concentration may lead to resolubilization of the condensed complexes into the bulk solution.[17] In single-molecule experiments, high concentrations of condensing agents may result in a decreased critical condensation force with a parabolic shape critical force-concentration curve. A number of studies refer to this phenomenon as re-entrant condensation.[18]
It is also necessary to distinguish DNA aggregation from DNA condensation, though much of the literature has confused the two processes. DNA aggregation is defined as a process of decreasing the volume occupied by DNA molecules by forming aggregates with an unordered organization, which is different from the ordered arrangement in DNA condensation. Moreover, in the aggregation process, the secondary structure of DNA can be altered to be other comformations such as the denatured state. While in the condensation process, the DNA conformation remains in the B-form. In morphology characterization experiments, it is often hard to distinguish the DNA aggregates and the DNA condensates. However, by vibrational circular dichroism (VCD) spectroscopy, the two processes can be well differentiated through the capability of inducing Ψ -type VCD spectra of DNA condensates.[19]
DNA is a polyelectrolyte dissociated in solution possessing a negatively charged backbone and surrounded by counterions carrying opposite charges. If the effective charge of DNA condensates is reversed to a positive charge through the binding of condensing agents, this will consequently lead to reversal of electrophoretic mobility in electrophoresis experiments. This phenomenon is known as charge inversion or charge reversal.[20] Another related concept is charge overcompensation, which refers to the phenomenon that excess counterions bind to the polyelectrolyte surface leading to overcompensation of the surface charges. Many studies consider the two phenomenon to be equal, however, it is better to distinguish between them.[21] For charge inversion, all ions associated with a polyelectrolyte should be included, since these ions contribute to the effective charge. However, for charge overcompensation, only the ions bound to the polyelectrolyte surface are considered. In other words, charge inversion always accompanies charge overcompensation, but the latter does not necessarily lead to the former.
The routes of in vitro DNA condensation can be classified into two categories. The first induces DNA condensation by inducing the attraction between different DNA parts, such as multivalent ion-induced condensation. The second induces DNA condensation by pushing together different DNA parts, such as the polymer and salt system scenario. The latter type of condensation is also called Ψ (psi, polymer and salt induced) condensation. The pushing force originates from the depletion forces of the crowding polymers; the presence of salts can neutralize the charges on the DNA, consequently decreasing the electrostatic resistance between different DNA parts. DNA condensing agents can be classified into two types based on the means of condensation: cationic agents, including multivalent cations, various cationic proteins, and cationic surfactants; and neutral poor solvents or crowding polymers such as ethanol, dextran, and polyethylene glycol. Counterions such as Na+ play different roles in the two types of condensation mechanisms. Specifically, in Ψ condensation, increasing Na+ concentration promotes condensation, whereas in cationic ion-induced DNA condensation, it has an impeding effect.
The experimental techniques used to study DNA condensation can be classified as ensemble methods or single-molecule methods. Ensemble methods, such as dynamic light scattering (DLS), osmotic pressure equilibrium, atomic force microscopy (AFM), and various spectrum analysis techniques, are based on collective measurements of numerous molecules in solution. Single-molecule methods, such as single-molecule fluorescence, optical tweezers (OT), and magnetic tweezers (MT), are based on measurements of single molecules.[22– 24]
The typical DNA condensate morphologies are rod, toroid, globule, pancake, and pearl-necklace structures (Fig. 3). The final DNA conformation is determined by many factors, such as solution properties, [25– 27] condensing agent structure, [28, 29] incubation conditions (for example, incubation time, condensing agent concentration, temperature, and Na+ (Mg2+ ) ion concentration).[30– 36] Previously, we studied the influence of several factors on the morphology of condensed DNA. The results of our studies and those of other researchers demonstrate that the conformation of condensed DNA is governed by competing hindering and promoting factors. The hindering factors include DNA rigidity, the electrostatic resistance between different DNA sections, and the limitation of dynamic factors such as the incubation time; whereas the promoting factors include the cationic ion screening effect, the attracting effect resulting from the electrostatic correlation between multivalent ions, the depletion forces of crowding polymers, the hydrophobic ability of cationic surfactants, and ion entropy in bulk solution. Previous studies indicate that in general, if the condensing ability of an agent is strong enough and it is incubated with DNA for a sufficient time period, the resulting conformation will usually be a compact globule [Fig. 3(b)]; moderate condensing abilities will result in a toroid or rod conformation [Figs. 3(a) and 3(c)]; weaker condensing abilities will favor loose structures such as a pancake-like conformation [Fig. 3(d)] or pearl-necklace structure [Fig. 3(e)]; if the length of the DNA molecules is short enough, a liquid crystal conformation is probable due to its rigidity (not shown in Fig. 3).
 | Fig. 3. Typical condensed DNA structures imaged by AFM.[31] (a) toroid; (b) globule; (c) rod; (d) pancake; (e) necklace. |
The Poisson– Boltzmann equation[37– 39] and Manning theory[40– 42] can depict the counterion distribution surrounding uncondensed DNA in solution. However, the remaining 7 Å – 12 Å water molecules in condensed DNA suggest equilibrium between attracting and resisting forces inside the condensate. Classical intermolecular force theory is unable to explain the forces inside the condensate. Therefore, many new theories have been suggested over the past decades, including the ion correlation theory, [7, 43, 44] hydration force theory, [45, 46] and electrostatic zipper theory.[47] However, the corresponding experiments for verifying and developing these theories are still in their infancy.
In terms of polymer physics, DNA condensation can be considered as a coil– globule transition. Thus, either the polymer theory or scaling theory can be applied to analyze this process.[48, 49] These theories predict a transition in the first order for lengthy macromolecules. Single-molecule fluorescence experiments confirmed that condensation is an all-or-none transition for single DNA molecules; however, DNA ensemble experiments indicate that the process is continuous.[50]
Single-molecule DNA condensation experiments involve DNA stretching and condensation dynamics, thus, many theories are aimed at elucidating these mechanisms.[51– 53]
Several theoretical models based on free energy minimization have been suggested to explain the conformations of DNA condensates.[54, 55]
The previous section outlined a preliminary classification of the theories relating to DNA condensation. We next introduce a number of these theories and the important concepts on which they are based.
According to the Poisson– Boltzmann (PB) theory, a charge is treated as a point charge and only the Coulomb interactions are considered, whereas the correlation between the charges is ignored. The charges on the surface of the polyelectrolyte are deemed to be evenly distributed, i.e. a mean field. The surface charge distribution is determined by the competition between electrostatic interactions and ion entropy in bulk solution. The Poisson equation is used to define the electrostatic interactions and the Boltzmann distribution determines the counterion distribution. The boundary condition is that the entire system is neutral. Polyelectrolytes such as DNA are often approximated as an isolated, infinite long cylinder. The cylindrical PB equation can then be used to obtain the counterion distribution. However, since this theory ignores many factors such as the excluded volume and the interactions between the counterions (correlation effect), it fails to explain the attraction between surfaces with like charges as is the case in DNA condensation.
In solution, DNA molecules coexist with counterions. However, how the counterions distribute around DNA and the conditions for counterion condensation on the DNA surface is worth considering. It should be noted that the concept of “ counterion condensation” used by Manning is completely different from “ DNA condensation” . The former refers to the aggregation of counterions on the DNA surface due to its electric field thus forming an electric double-layer-like structure. Manning defined counterion condensation as non-localized binding (or territorial binding). This type of binding is characterized by the ions within the bound region retaining mobility and the existence of a diffuse chemical potential stemming from the concentration difference with the bulk solution. In contrast, the concept of localized binding is characterized by the ions binding closely to the polyelectrolyte resulting in a lack of mobility. The Manning theory was developed during the 1960s to explain counterion condensation on polyelectrolytes based on the concept of non-localized binding.[42] The theory is concise and has been verified by many experiments. Here we detail its main points.
Consider a polyelectrolyte chain consists of Zp-valent charged groups. Every charged group is seen as a point charge carrying Zpe with a mean separation b. Suppose the valence of the counterion is Zc. Define β = Zpe/b, ξ = e2/ε kBTb = lB/b, where lB is the Bjerrum length. The latter represents the Manning parameter, which is an estimation of the charge density of a polyelectrolyte (note that a Gaussian unit is used). Approximating the polyelectrolyte as an infinite long line charge, the electrostatic energy of a counterion which is r distant from the line charge is given by uip = − 2Zceβ ln (r)/ε . The contribution Ai (r0) to the phase integral of the region in which the counterions are at a distance r ≤ r0 is
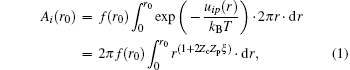
where f(r0) is a finite factor. If ξ ≥ | ZcZp| − 1, equation (1) diverges. To avoid this, counterions tend to condense on a polyelectrolyte surface to screen its charges. Then, the effective charge qnet is lowered from q = Zpe to qnet = (1 − | Zc| θ c)Zpe = (1 − | Zc| θ c)q, where θ c is the number of counterions bound to every charged group. Consequently, the mean charge separation is increased, which results in ξ net = (1 − | Zc| θ c)ξ . When ξ net is lowered to a critical value | ZcZp| − 1, the counterion condensation reaches equilibrium. For DNA, Zp = − 1, b = 1.7 Å , T is set at 298 K (room temperature), ε is set as the dielectric constant of water 82, and ξ is calculated to be 4.2, which is greater than | ZcZp| − 1. Based on this conclusion we get:
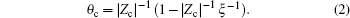
Alternatively, define the charge fraction f = 1 − | Zc| θ c, which identifies the fraction of charges in the polyelectrolyte which are not neutralized. Hence
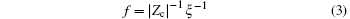
for monovalent counterions such as Na+ , f = 0.24; for divalent counterions such as Mg2+ , f = 0.12.
In summary, the main conclusion of the Manning condensation theory is that if the charge density of a polyelectrolyte is greater than a critical value, the counterions will condense on the polyelectrolyte surface to lower the charge density to a given value. This type of counterion condensation occurs when the Coulomb electrostatic potential exceeds the influence of counterion entropy.
If the bulk solution contains two types of counterions, such as monovalent and divalent counterions, Manning’ s deduction provides the following equation for describing θ 1 and θ 2:


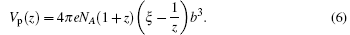
In the above equations, Z1, c1, and θ 1 represent the valence, mole concentration, the volume of the binding region of one mole polyelectrolyte, and the number of counterions bound to every charged group referring to monovalent ions, respectively. Z2, c2, and θ 2 are the corresponding values referring to divalent ions. Vp(z) is the volume of the Z-valent counterion binding region for every mole of polyelectrolyte with a unit of cm3/mol. κ is the inverse of the Debye– Hü ckel screening parameter. Equations (4) and (5) can be solved by numerical iteration, hence the charge fraction f = Z1θ 1 + Z2θ 2.
The Manning theory applies excellently to low-valent counterion (such as Na+ , Mg2+ ) cases. Various titration experiments have shown that the neutralized charge fraction in DNA agrees well with the theory. However, when the counterion valence is three or higher, the theory can no longer explain the induced DNA condensation phenomenon. In DNA condensates, the fraction of neutralization no longer maintains specific values such as f = 1 − (3ξ )− 1 ≅ 92% (for trivalent ions). On the contrary, the fraction may increase to such a level that the effective charge of the DNA is reversed, i.e. charge inversion. Moreover, similar to the PB theory, the Manning theory is unable to explain the phenomenon of like-charge DNA surfaces being attracted to each other during the condensation process. Despite this, the Manning theory is still a successful theory proposed on the basis of Occam’ s razor; it provides concise testable conclusions based on several premises. Numerous experiments have verified the theory; Section 8 illustrates that the theory can even be applied to interpret reentrant condensation behavior during multivalent ion-induced DNA condensation. In cases of a non-applicable phenomenon, some premises may no longer be sustained; for example, the binding is no longer non-localized.
A feasible explanation as to why the Manning theory fails to explain cases of multivalent ions is based on the counterion correlation theory.[7, 56] The premise of the theory is that the electrostatic correlation between the counterions is significant when the valence of the counterion is three or higher, in comparison to monovalent and divalent counterions, where thermal fluctuation counterbalances the electrostatic correlation. Coulomb’ s coupling parameter is defined as:
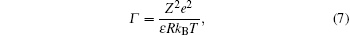
where Z is the valence of the counterion, kBT is thermal energy, R is the mean distance between the counterions. For a Wigner crystal (Fig. 4), π R2 = 1/n (n = σ /Ze, is the counterion concentration), 
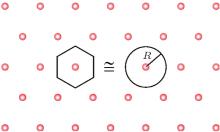 | Fig. 4. The Wigner– Seitz crystal.[7] |
Grosberg, Nguyen, and Shklovskii introduced the Wigner Crystal concept to explain electrostatic correlation. The main result of the Wigner theory is that a gas of electrons moving in a uniform, inert, and neutralizing background (the plasma system) will crystallize and form a lattice structure if the electron density is lower than a critical value. This is because the potential energy dominates the kinetic energy at low densities and consequently the electrons arrange into a crystal structure in order to minimize the potential energy. This theory has an important dimensionless parameter, the Wigner– Seitz radius at zero temperature, which can be viewed as an estimation of the average electron spacing. For two-dimensional one component plasma, the correlation energy and chemical potential of each ion are
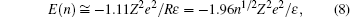

Here R is the radius of a Wigner– Seitz crystal with its cell approximated as a disk (Fig. 4).
Based on the proposed correlation energy and chemical potential, one important conclusion is the prediction of charge inversion.[20, 44] In electrophoresis experiments, charge inversion is often shown to reverse complex mobility. Section 8 will illustrate how this theory can be used to explain DNA reentrant condensation behavior.
Though the counterion electrostatic correlation theory can explain the attraction between like-charge polyelectrolytes such as DNA, it cannot explain cation specificity. For example, it is has been shown that transition metal ions (Mn2+ and Cd2+ ) cause guanine-cytosine (GC) rich DNA condensation despite their low affinity for phosphate, whereas alkali earth metal ions (Mg2+ , Ca2+ ) cannot condense DNA in spite of their high affinity for phosphate. To explain this, Kornyshev and Leikin suggested that details of the surface charge pattern may determine the specificity and energetics of DNA condensation. They proposed an electrostatic interaction theory to explain cation specificity in DNA condensation.[47] Counterion condensation in helix grooves results in axial charge separation, which enables the attraction between opposite charges along the DNA– DNA contact and forms an electrostatic zipper-like structure. This theory also uses the counterion condensation concept; counterion condensation on the phosphate strand is thought to reduce the attraction because of weaker charge separation, which is consistent with the observation that Mg2+ and Ca2+ cannot induce DNA condensation despite their high affinity for phosphate. In contrast, the counterion condensation of transition metal ions, such as Mn2+ , onto the major groove of the DNA leads to attraction between DNA regions.
The advantage of the electrostatic zipper theory is that it considers the helical structure of the DNA molecule and the different ion binding patterns on DNA. However, similar to other theories, the ion size effect is not included and hence it may be difficult to use the theory to explain DNA condensation caused by ions with larger sizes.
The hydration force concept was developed based on measurements of the osmotic pressure as a function of the distance between the polymers. It was found that when the distance between parallel aligned DNA molecules is 5 Å – 15 Å , ion strength does not have a significant effect on the interaction force; the repulsion pressure decays exponentially with a characteristic decay length of 2.5 Å – 3.5 Å .[57]
The precise physical mechanism of hydration force remains unclear. It is assumed that the force originates from the reconfiguration of water molecules near condensed polymers such as DNA.[58, 59] As dipoles, water molecules orderly arrange near DNA because of its electric field. The order degree decays exponentially with the distance from DNA. Leikin et al. suggested that the magnitude of the hydration force is related to the order degree of the water molecules on the surface.[45] Attraction is due to complementary arrangement and repulsion results from symmetrical arrangement. It is difficult to determine the magnitude of the force since it is the sum of weak interactions between numerous molecules. In spite of this, a number of general conclusions regarding the order parameter formalism have been developed. Consider two similar, homogenous planar surfaces separated by distance h. The repulsion pressure is
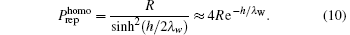
If the surfaces are complementary, the pressure is attractive with a magnitude of

Here R and A are coefficients, λ W is the water correlation length (approximately 4 Å – 5 Å . If the surfaces have a lattice structure with periodicity a, homogeneous pressure is replaced by inhomogeneous pressure:
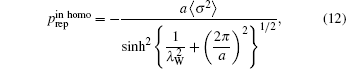
where σ is the surface charge density. For B-DNA, a = 34 Å , λ W = 4 Å – 5 Å . The effective correlation length is
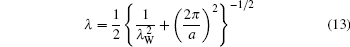
with a value of 1.6 Å ∼ 1.8 Å , which is comparable with experimental measurements.
The drawback of the hydration force theory is that it is an experiment-oriented theory, which can only explain the resisting and attracting forces involved in DNA condensation; the physical elements remain unclear and untested.
Consider a macromolecule consisting of N monomer segments with a persistent length Lp and width d. The free energy of each macromolecule can be expressed as a function of the swelling coefficient α (= R/R0):

where R and R0 are the gyration radius of the real chain and the Gaussian chain, B and C are the second and third virial coefficients. The first term on the right side of the equation describes elastic free energy and the second and third terms are the free energy of interaction. Minimizing the free energy F over α results in the following equation:

where 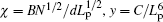
The coil– globule transition theory successfully explains experimental observations of the coexistence phenomenon. Specifically, single-molecule fluorescence experiments have shown that the coil conformation coexists with the globule conformation.[60, 61] However, it should be noted that the coil– globule theory is in the structure of the theory proposed by Lifschitz, [62] which states that the virial expansion only applies to low DNA segment concentrations. Since the concentration in DNA condensates can be quite high and the polyelectrolyte nature of DNA is not directly reflected in this theory, more detailed studies are not possible.
Compared with ensemble methods, single-molecule techniques possess a unique viewpoint and several advantages. For example, the elastic behavior of DNA can be measured directly and the persistent length of DNA can be obtained from these measurements, [63, 64] which is more accurate and direct than traditional methods.[65] However, the incorporation of old ensemble-research concepts into single-molecule experiments requires some consideration. Moreover, single-molecule measurements can be used to test distinct theories. In the following section we introduce single-molecule experimental advances in the field of DNA condensation that involve these two aspects.
The phenomenon of cooperative binding is a common concept in biochemistry; [66] when one ligand molecule binds to a macromolecule, the binding affinity of other ligand molecules may be strengthened or weakened. In 1910, Hill proposed an equation to quantify this effect in order to explain the sigmoidal shape of a curve estimating hemoglobin oxygen saturation as a function of the partial pressure. The equation is:

where θ is fractional occupancy (the ratio of the number of bound sites to the number of total sites), [L] denotes ligand concentration, Kd denotes association constant, and n is the Hill coefficient describing cooperativity. If n = 1, the binding is independent of the concentration of the bound ligands. If n > 1, the binding shows positive cooperativity, whereas cooperativity is negative if n < 1. Using this equation, Hill confirmed that the binding of oxygen molecules to hemoglobin is cooperative and that the Hill coefficient is 2.8∼ 3.
DNA condensation can be viewed as a process of ligand molecules (e.g. multivalent ions or proteins) binding to receptor molecules (DNA). If the binding is cooperative, it should be observed in single-molecule DNA condensation experiments. Consider a suspending DNA molecule with an initial end-to-end length L0 micromanipulated by either the MT (magnetic tweezers) or OT (optical tweezers) method. When ligand molecules with a cooperative effect are added, it can be assumed that the cooperative effect is proportional to the number of bound molecules. Binding leads to the DNA length L gradually shortening. Therefore, the number of bound molecules is assumed to be proportional to L0 − L. At the same time, the shortening of DNA length results in a decrease of the effective interaction volume, which is proportional to L − Lf. Here Lf is the final length of the saturated DNA. It is assumed that within the corresponding volume, ligand molecules cannot bind to the DNA. Combining these two terms yields an equation describing the DNA condensation rate:

where K = k · Cp · k0, k is reaction constant, Cp is ligand concentration, k0 is the number of ligands to condense DNA per unit length. Solving the equation gives a length-time curve with a sigmoidal shape (Fig. 5), which fits well with experimental measurements.[67] That is to say, cooperative behavior is reflected in the sigmoidal shape of the length-time curve of single-molecule DNA condensation measurements. Hence the old concept of “ cooperativity” is reinterpreted in the new single-molecule experiment.
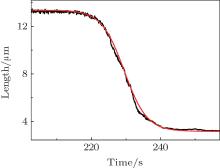 | Fig. 5. Comparison between the DNA condensation curve and the cooperative behavior model.[67] |
Resolubilization is another concept developed through ensemble experiments. Pelta et al. studied polyamine and cobalthexamine-induced DNA condensation by measuring the amount of uncondensed DNA in the supernatant.[17] They found that the addition of multivalent cations leads initially to DNA precipitation; further addition leads to the resolubilization of the DNA condensates, which is confirmed by the increased DNA concentration in the supernatant.
Resolubilzation is manifested as reentrant condensation behavior (Fig. 6) in single-molecule experiments. Besteman et al. studied charge inversion accompanied by DNA condensation caused by multivalent ions using MT.[68] They initially used the DLS method to measure the mobility of condensed DNA particles. A change in mobility from negative to positive indicates charge inversion. When the concentration of spermine in 1-mM Tris buffer is greater than 0.5 mM, mobility becomes positive. Increasing the Tris concentration to 10-mM hinders charge inversion, inducing the charge-inversion concentration of spermine to increase to 1 mM. The addition of 50-mM KCl salt leads to the disappearance of charge inversion at spermine concentrations < 3 mM. Next, they used MT experiments to elucidate how charge inversion hinders DNA condensation. The measurements of the condensation force (Fc) as a function of spermine concentration (c) shows that the force increases to a maximum at c = 10− 3 M– 10− 2 M, followed by a gradual decrease in Fc. When c > 0.5 M, condensation ceases. The decrease in Fc indicates reentrant condensation at the single-molecule level. The coincidence of the measured and extrapolated charge inversion concentrations and the peak concentrations of the condensation force measurements suggests that charge inversion results in peak Fc, consistent with the prediction of the counterion correlation theory. The applied theory of this research was proposed by Nguyen et al.; [44] the main point of the theory is that when a polyelectrolyte is neutralized to carry sufficient low effective charges, the electrostatic correlation overcomes the electrostatic repulsion resulting in condensation. However, when the effective charge of the polyelectrolyte is reversed, electrostatic repulsion becomes dominant again and reentrant condensation occurs. This is another example of an old concept represented as a new phenomenon in single-molecule experiments.
Todd et al. found a similar phenomenon in multivalent ion-induced DNA condensation and provided an alternate explanation for it.[69, 70] Combining MT and osmotic stress on DNA assemblies, they separated the attractive and repulsive components of the interaction force inside condensed DNA. Two invariant properties of multivalent cation-mediated DNA interactions were identified. At force-balance equilibrium, repulsive forces decay exponentially with a cation-independent 2.3 Å ± 0.1 Å decay length; the decay length of the attractive forces is constantly 2.3± 0.2 times higher than the repulsive component. These decay lengths were then used to test current theories. The counterion correlation theory predicts that the ratio of attractive force to repulsive force is between 1.2– 1.8, which is inconsistent with the measurements. The Debye– Hü ckel interaction and order parameter formalism for hydration forces theories predict the ratio is approximately 2, which agrees well with the data.
Since the counterion correlation theory is not consistent with experimental results, how can reentrant condensation behavior be explained? Todd et al. noticed that reentrant condensation occurs near the solubility limit of the multivalent cation salt. Near this limit, lower-valent anion-associated multivalent cations are likely to form, which increase the energetic cost for neutralizing DNA. For example, trivalent cations associate with monovalent anions and form divalent ion pairs. Divalent ion pairs have lower condensing abilities than multivalent ions, therefore it is thought that high concentrations of multivalent cations lead to decreased DNA condensation force. Based on this, they successfully used the traditional Manning theory to explain their data.
These two groups have provided different explanations for the same phenomenon based on their measurements and analysis. According to the counterion correlation theory, charge inversion always leads to reentrant condensation, but is reentrant condensation necessarily caused by charge inversion? Several experimental points need to be taken into consideration in order to answer this question. Firstly, charge inversion does exist in DNA condensation; secondly, the critical concentrations at which charge inversion occurs are not highly agreeable with the critical reentrant condensation concentration; thirdly, in order to apply their model, Todd et al. used the simplification that the DNA condensate is neutral at high multivalent ion concentrations; and lastly, the experimental conditions of the two studies were dissimilar. Based on these facts, it is best to be cautious in reaching a final conclusion until further experimental verification is obtained.
We recently reported that this reentrant behavior also occurs in the Ψ condensation.[71] The MT measurements show that by increasing Mg2+ concentration, the DNA condensation in polyethylene glycol (PEG) solution undergoes a reentrant process, which was verified by the decreased critical condensation force. The critical concentration of Mg2+ at which reentrant condensation occurred in the study was as low as ∼ 3 mM (in 30% PEG 6000 solution). Such an observation seems to rule out the possibility of the ion pair formation, because Mg2+ has lower affinity to anions compared with the cases of multi-valent cations, and consequently the ion pair effect is negligible in the studied concentration range. Nevertheless, the difference between the two similar reentrant behaviors in the two different scenarios (i.e., the Ψ condensation and the multi-valent cation-induced DNA condensation) remains to be investigated further. In spite of this, the predictions of the theories can be either proved or disproved by the above-mentioned single molecule experiments. Therefore, additional and similar experiments should be conducted to thoroughly evaluate the various theories.
This review clarifies and distinguishes between the related concepts of DNA condensation and introduces various concept-related theories. For uncondensed DNA, the PB theory and Manning theory are often used to explain the counterion distribution surrounding DNA. Both theories consider DNA as an infinite long cylinder with charges on its surface. Though the PB theory has a wider application range, it seems that the Manning theory captures the main feature of counterion condensation on DNA. However, both theories cannot fully explain DNA condensation since they ignore the counterion correlation effect. Therefore, the counterion correlation theory, which includes the electrostatic interactions between the counterions, was proposed to better explain DNA condensation. The electrostatic zipper theory, which considers the helical structure of DNA and the resulting different binding patterns, can account for the ion specificity in DNA condensation induced by transition metal ions. Although the hydration force and coil– globule transition theory do not directly consider the nature of DNA as a polyelectrolyte, they do have their respective applications for explaining the experimental facts of DNA condensation. Taken together, DNA condensation is still a challenging issue in spite of the multi-field approaches used; at present, no theory has completely clarified this problem. The primary reason for this is that most theories ignore several important factors. Specifically, almost all of the theories do not take into consideration the size effect of the counterions. None of the theories, aside from the electrostatic zipper theory, consider the helical structure of DNA, which may be an important factor affecting the binding mode and thus ion specificity. The second reason is the lack of sufficient experimental data to prove or disprove the related theories, which could inhibit further development of these theories. Many theories are complicated with a lot of mathematical details or make too many simplifications, whereas the predictions that can be proved or disproved using the present experimental methods are lacking to some extent.
The old concepts introduced by ensemble experiments can be reinterpreted in single-molecule experiments. Two such examples have been presented in this review, including the concepts of cooperativity and resolubilization in single-molecule experiments. Moreover, the single-molecule experiments introduced in Section 8 are good examples of using experiments to prove or disprove theories. However, similar experiments are still rare. In our opinion, when a scientific issue is unresolved, large amounts of experimental measurements need to be conducted and the corresponding theory or model need to be developed based on the results.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|
| 66 |
|
| 67 |
|
| 68 |
|
| 69 |
|
| 70 |
|
| 71 |
|