The ABO₃-type perovskite oxides have been extensively studied, because of their novel physics and broad technical applications.^[1] Among abundant functional perovskite compounds, ferroelectric materials, such as BaTiO₃ and PbTiO₃, have been known for a long time and are acquiring increasing importance in the modern electronic industry where their unique properties are utilized in capacitors and piezoelectric transducers.^[2] In addition, the partial Zr-substituted PbTiO₃ (Pb(Zr, Ti)O₃) is widely used to produce the ferroelectric random access memory (FeRAM) and other devices^[3] due to its principal advantages of relatively low crystallization temperature, compatibility with complementary metal oxide semiconductor (CMOS), and high remanent polarizations.^[4] However, although PbTiO₃ and Pb(Zr, Ti)O₃ are very industrially valuable, they are environmentally unfriendly due to the toxicity of Pb. It remains a challenging problem to pursue the Pb-free ferroelectrics to replace PbTiO₃/Pb(Zr, Ti)O₃ in industry. In recent years, there have been a few experimental studies on Ba(Zr,   Ti)O₃ thin films, which can be considered as a clone of Pb(Zr, Ti)O₃. Although its ferroelectric performance is not so prominent compared with Pb(Zr, Ti)O₃, it provides an alternative choice to environmental protection. Compared with the intensively studied Pb(Zr, Ti)O₃, the Ba(Zr, Ti)O₃ are investigated very little. Although there has been a little experimental work on this material, ^{[5– 12]} a systematic theoretical study on its physical mechanism of relaxor ferroelectricity of Ba(Zr,   Ti)O₃ is still lacking, to the best of our knowledge. In fact, the physical issues involved in Ba(Zr, Ti)O₃ are not identical to those in Pb(Zr, Ti)O₃, since Pb²⁺ itself contributes to a significant portion of polarization. In this sense, a theoretical investigation on Ba(Zr, Ti)O₃ is physically meaningful and useful for its applications.

BaTiO₃ is a typical ferroelectric perovskite. Its phase transition from para-electric state to ferroelectric state has been experimentally studied using various techniques. With reducing temperature, it presents three sequential phase transitions from cubic to tetragonal at 393  K, from tetragonal to orthorhombic at 278  K, and from orthorhombic to rhombohedral at 183  K.^{[13, 14]} The para-electric phase is cubic (space group Pm3m) with an experimental lattice constant of 4.0045  Å .^{[14, 15]} Among all the ferroelectric states, the tetragonal ferroelectric state is the most interesting and has been widely studied previously.^[16] The tetragonal ferroelectric phase at room temperature belongs to the space group P4mm. The experimental measured lattice constants are a = 3.9945  Å and c = 4.0335  Å . The fractional atomic positions are Ba at (0, 0, 0), Ti at (0.5, 0.5, 0.514), O₁ at (0.5, 0.5, − 0.025), O₂ at (0.0, 0.5, 0.488), and O₃ at (0.5, 0.0, 0.488).^{[14, 17]} Its spontaneous polarization (P_S) is 26  μ C/cm² along the tetragonal c axis.^{[18, 19]} The partial substitutions of Zr occupies the B-sites (Ti site) randomly.

In this work, the ferroelectricity of Ba(Zr, Ti)O₃ will be studied with the supercell model by the first-principles theory. Our density functional theory (DFT) calculations indicate that in general the dipole moment decreases with Zr substitution. The ferroelectric properties diverge among different structures, which greatly depends on the arrangements of Ti and Zr ions. In addition, the model based on thermal statistics reveals the synthesis-temperature-dependent polarization of Ba(Zr, Ti)O₃. Our theoretical results can explain some experimental observations like relaxor ferroelectricity and help to improve its ferroelectric performance.

Our DFT calculations were performed using Vienna ab initio simulation package (VASP)^{[20, 21]} with the PBEsol (Perdew– Burke– Ernzerhof-revised)^[22] parameterization of the generalized gradient approximation plus U(GGA + U).^{[23– 25]} The choice of PBEsol is crucial to give an accurate description of the lattice structure of titanates, while the traditional PBE often fails for ferroelectric titanates. All calculations, including the lattice relaxation and static calculations, have been done by applying the Hubbard U_eff (= U − J) to the d-orbitals of Ti ion through using the Dudarev implementation.^[26] The plane-wave cutoff of 550  eV is adopted. A 9 × 9 × 9/5 × 5 × 5 Monkhorst– Pack k-point sample centered at the Γ point is used in combination with the tetrahedron method for the pure BaTiO₃ and the 2 × 2 × 2 supercell respectively. The inner atomic positions as well as the lattice constants are fully optimized as the Hellman– Feynman forces are converged to less than 5  meV/Å . The electrical polarization is calculated using the standard Berry-phase approach.^[27]

Before the calculation of Ba(Zr, Ti)O₃, the physical properties of BaTiO₃ are checked first. The tetragonal structure of the ferroelectric state is fully optimized with various U_eff values ranging from 0  eV to 4  eV in steps of 1  eV. Then the electric dipole moment and band gap are calculated using the fully relaxed structures. As shown in Fig.  1, the dipole moment varies from 30.27  μ C/cm² to 1.21  μ C/cm² and the band gap increases with increasing U_eff. When U_eff = 1  eV, the fully relaxed lattice gives a = 3.988  Å and c = 4.044  Å (Fig.  1(c)) and the ferroelectric dipole moment is just 25.15  μ C/cm² (Fig.  1(a)) which are fairly close to the experimental data, implying a proper U_eff for BaTiO₃. Although the band gap of ∼ 2.0  eV (Fig.  1(b)) is a little narrower than the experiment value (2.8  eV to 3  eV^[28]), it is still acceptable when considering the well-known underestimation of band gap in DFT calculations. Also, we check the suitable U_eff for Zr ion. In the DFT calculation, the optimized lattice constant for cubic BaZrO₃ increases with U_eff. When U_eff = 0  eV, the lattice constant gives 4.215  Å , which is closest to the experiment value (4.19  Å ).^[29] This is also reasonable when considering Zr 4d orbitals whose Hubbard U is much weaker than that of the 3d orbitals. Thus, in the following calculations, U_eff = 1  eV and 0  eV will be adopted by default for Ti and Zr d orbitals, respectively.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Physical properties of BaTiO3 in our DFT calculation as a function of Ueff. (a) The dipole moment. (b) The band gap. (c) The lattice constants.

Subsequently, the energies and dipoles for para-electric and ferroelectric BaZr_0.5Ti_0.5O₃ are calculated using a 2 × 2 × 2 supercell which includes eight chemical units. Since in real materials Zr and Ti may be randomly distributed, here all possible Zr– Ti configurations are tested in the supercell. The combination number is . Considering the space symmetry, there are only fifteen independent configurations for the ferroelectric state, which are further reduced to five independent configurations for the para-electric state, which are summarized in Table  1. The degeneracies of these configurations are also presented.

Table 1.

Table 1.

Table 1. The DFT results of all models for BaZr0.5Ti0.5O3 supercell. In the 2× 2× 2 supercell, the red (dark gray) balls are titanium ions, and the yellow (light gray) balls are zirconium ions. The barium and oxygen ions are not shown here. The energy difference Δ E in unit of meV between various para-electric models is E(x)– E(V) and that between various ferroelectric models is E(x)– E(O) for the supercell. The values of dipole moment (Pc) along the c axis for fifteen independent ferroelectric states are also shown in units of μ C/cm2. Paraelectric Ferroelectric Model Δ E Model Degeneracy Δ E Pc I 846 A 4 633 21.52 B 1 846 1.85 C 1 847 1.96 II 546 D 4 545 0.60 E 2 212 23.73 III 715 F 8 652 12.84 G 4 589 12.85 H 4 589 12.87 IV 498 I 8 403 13.42 J 4 500 2.14 K 8 403 12.92 L 8 625 14.60 M 4 500 2.21 N 8 625 14.71 V 0 O 2 0 0.21

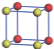
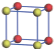
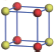
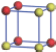
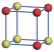
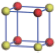
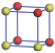
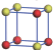
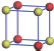
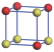
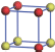
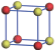
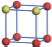
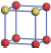
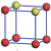
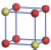
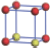
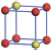
Table 1. The DFT results of all models for BaZr0.5Ti0.5O3 supercell. In the 2× 2× 2 supercell, the red (dark gray) balls are titanium ions, and the yellow (light gray) balls are zirconium ions. The barium and oxygen ions are not shown here. The energy difference Δ E in unit of meV between various para-electric models is E(x)– E(V) and that between various ferroelectric models is E(x)– E(O) for the supercell. The values of dipole moment (Pc) along the c axis for fifteen independent ferroelectric states are also shown in units of μ C/cm2.

For each independent configuration, both the internal atom positions and the lattice framework are relaxed to obtain the optimal structure. Then the energy and dipole moment for the relaxed structure are calculated as also shown in Table  1. According to Table  1, among all configurations, the one named V/O has the lowest energy despite the para-electric and ferroelectric state, in which Zr and Ti are alternatively ordered along all three axes. Its relaxed lattice gives a = b = 8.204  Å , and c = 8.205  Å for the ferroelectric state, whose tetragonality (namely the c/a ratio) is very weak. As expected, its dipole moment along the c-axis is only 0.21  μ C/cm², which is a very tiny value. As shown in Table  1, the calculated dipole moments are very divergent among different configurations, which greatly depends on the Zr– Ti arrangement. The maximum value is 23.73  μ C/cm² for the configuration E, which is very close to the BaTiO₃ itself. Thus, our result suggests that for real Ba(Zr, Ti)O₃, the quenching disorders of Zr and Ti will make the system quite non-uniform regarding its local ferroelectric properties, rendering the relaxor ferroelectric behavior.^{[30, 31]}

In order to obtain the effective polarization of real Ba(Zr,   Ti)O₃, the thermal average based on the Boltzman equation ((p ∼ D· exp(– E/k_BT) where p is the probability of each independent configuration, D is the degeneracy, E is the energy, k_B is the Boltzman constant, and T is temperature) is performed to simulate the distribution of Zr– Ti configuration during the high-temperature synthesis. After the thermal equilibrium at the high temperature reaction, the crystal forms and then is cooled down to the room temperature. Then the distribution of Zr– Ti configuration is modeled to be dependent on synthesis temperature. At such a high synthesis temperature, Ba(Zr, Ti)O₃ is in its para-electric state since the ferroelectric Curie temperature of BaTiO₃ is only 393  K, ^[14] much lower than typical synthesis temperatures which can be higher than 1000  K.

Then the probabilities for five para-electric states are calculated as a function of the synthesis temperature. As shown in Fig.  2(a), the lowest energy state V is dominant when the synthesis temperature is relatively low. With increasing temperature, the portion of the second lowest energy state IV increases significantly and even overcomes the energy state V finally, since the degeneracy of state IV is larger than that of state V. Then the contribution of polarization from each configuration is calculated considering the probability of corresponding ferroelectric state and its dipole moment. As shown in Fig.  2(b), it is clear that in the whole temperature range the primary source state is from the configuration IV, while other states are all negligible with respect to ferroelectric polarization. As shown in Fig.  2(c), the total polarization increases almost linearly from 0.93  μ C/cm² to 6.74  μ C/cm² with increasing synthesis temperature from 1000  K to 2000  K. Our result suggests that a higher synthesis temperature can facilitate the effective polarization of Ba(Zr, Ti)O₃.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) and (d) Synthesis temperature-dependent probabilities for various para-electric states. (b) and (e) Synthesis temperature-dependent dipole moment contributions of various ferroelectric states evolving from corresponding para-electric. (c) and (f) Synthesis temperature-dependent total dipole moments for the composites.

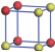
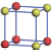
According to above results of BaZr_0.5Ti_0.5O₃, the system becomes relaxor ferroelectric for the partial substitution of Zr. However the effective polarization is greatly suppressed. Therefore, to keep a balance between the relaxor and polarization, less substitution may be a better choice. In the following, the concentration of Zr is reduced to 25%, giving BaZr_0.25Ti_0.75O₃. Still using the 2 × 2 × 2 supercell, despite the total combinations, there are seven independent configurations for the ferroelectric state and only three independent configurations for the para-electric state as summarized in Table  2. By performing the same processes (relaxation and static calculation), the energies and dipole moments for relaxed structures are obtained, which are also shown in Table  2. According to Table  2, the configuration II has the lowest energy in the para-electric state and its corresponding ferroelectric branch. Unlike the above half-substituted case, the configuration B processes the maximum dipole moment (28.79  μ C/cm²) along the c axis. Even the minimum dipole moment reaches 16.65  μ C/cm² as indicated in the configuration E. Then the probabilities of three para-electric configurations, their corresponding ferroelectric contributions, and the total polarization are calculated each as a function of synthesis temperature. According to Figs.  2(d)– 2(f), in the whole temperature range from 1000  K to 2000  K, the configuration II is a dominant one and contributes most to polarization. The total ferroelectric polarization only slightly changes from 17.64  μ C/cm² to 18.06  μ C/cm² with the increase of synthesis temperature. In this sense, the quarter-substituted Ba(Zr,   Ti)O₃ is more likely to be a normal ferroelectric while its relaxor behavior is not prominent.

Table 2.

Table 2.

Table 2. DFT results of all models for BaZr0.25Ti0.75O3 supercell. Titanium ions: red (dark gray) balls; zirconium ions: yellow (light gray) balls. Paraelectric Ferroelectric Model Δ E Model Degeneracy Δ E Pc I 260 A 4 299 16.97 B 4 152 28.79 C 4 299 16.99 II 0 D 2 0.04 18.49 E 8 40 16.65 F 2 0 18.52 III 76 G 4 76 18.88

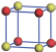
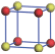
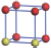
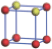
Table 2. DFT results of all models for BaZr0.25Ti0.75O3 supercell. Titanium ions: red (dark gray) balls; zirconium ions: yellow (light gray) balls.

In this work, the relaxor ferroelectric Ba(Zr, Ti)O₃ supercells are studied based on the density functional theory and thermal statistics. For the half-substituted case, divergence of ferroelectric dipole moments is found among different Zr– Ti configurations. Thus, the well-known relaxor behavior of Ba(Zr, Ti)O₃ can be attributed to the quenching disorder which gives rise to the non-uniform ferroelectric properties. In addition, our calculation indicates that the effective total polarization increases with the synthesis temperature increasing, which may be helpful to improve the ferroelectric performance of real material. In contrast, the quarter-substituted Ba(Zr, Ti)O₃ shows different behaviors, which is more likely to be a normal ferroelectric instead of a relaxor.