†Corresponding author. E-mail: wqyu_phy@ruc.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11374364 and 11222433), the National Basic Research Program of China (Grant No. 2011CBA00112). Research at McMaster University supported by the Natural Sciences and Engineering Research Council. Work at North China Electric Power University supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry.
We synthesized a quasi-two-dimensional distorted triangular lattice antiferromagnet Ca3CoNb2O9, in which the effective spin of Co2+ is 1/2 at low temperatures, whose magnetic properties were studied by dc susceptibility and magnetization techniques. The x-ray diffraction confirms the quality of our powder samples. The large Weiss constant θCW∼ −55 K and the low Neel temperature TN∼ 1.45 K give a frustration factor f = | θCW/ TN | ≈ 38, suggesting that Ca3CoNb2O9 resides in strong frustration regime. Slightly below TN, deviation between the susceptibility data under zero-field cooling (ZFC) and field cooling (FC) is observed. A new magnetic state with 1/3 of the saturate magnetization Ms is suggested in the magnetization curve at 0.46 K. Our study indicates that Ca3CoNb2O9 is an interesting material to investigate magnetism in triangular lattice antiferromagnets with weak anisotropy.
Geometrically frustrated classical/quantum magnets, in which the simultaneous minimization of local interaction energies cannot compromise with lattice geometry, have attracted a lot of research interest in condensed matter physics in recent years due to their novel magnetic orders and exotic excitations.[1– 3] The two-dimensional (2D) triangular-lattice Heisenberg antiferromagnet (TLHAF) is a paradigmatic example of frustrated magnet. Theoretical studies have reached a consensus that the ground state of the regular TLHAF with S = 1/2 selects the 120° non-collinear structure in the absence of field, which is similar to classical Heisenberg model.[4– 6] While under external field, the quantum fluctuations can stabilize a novel up-up-down quantum state, with a corresponding 1/3 plateau in the magnetization process.[7– 11] This model has given an excellent description on the magnetism of compounds such as Ba3CoSb2O9, [12] Ba3NiNb2O9, [13] and Ba3CoNb2O9.[14]
For the TLHAF with spatially anisotropic exchange, for example Cs2CuBr4, in addition to the up-up-down phase, many other phases with 1/2, 5/9, and 2/3 of Ms were observed in the magnetization curve.[15] Theoretical studies suggested that the interplay of spatially anisotropic interactions and quantum fluctuations should play an important role in new phases of Cr2CuBr4.[11, 15, 16] Therefore, it is of great interest to explore novel magnetic states in distorted triangular lattice antiferromagnets (DTLAF).
Recently, a new DTLAF material Ca3CoNb2O9 was reported, whose structure was determined by neutron powder diffraction, [17] but its magnetism has not been studied yet. As shown in Fig. 1(a), Ca3CoNb2O9 crystallizes in monoclinic structure (space group P21/c). There are two inequivalent Co2+ ions coordinated in two kinds of twisted CoO6 octahedra which are shown by an enlarged view [see Fig. 1(b)]. The Co2+ ions form almost perfect equilateral-triangular lattice layers parallel to the ab plane and are separated by two nonmagnetic NbO6 octahedra and Ca2+ ions. The distance between Co(1)– Co(1), Co(1)– Co(2), Co(2)– Co(2) are 0.5462 Å , 0.5521 Å , and 0.5462 Å , respectively. Considering the nonuniformity of Co2+ sites, there should be three different dominant exchange interactions between nearest neighboring Co2+ ions for Ca3CoNb2O9, which are labeled as J1, J2, and J3 respectively [Fig. 1(c)], the values of them need to be determined by future work. Meanwhile, due to the loss of an inversion center between Co(1) and Co(2), Dzyaloshinsky– Moriya (DM) interactions should also present in Ca3CoNb2O9. Therefore, this represents a prototype TLAFM system with spatial anisotropy and DM interactions.
In this work, we report our magnetization studies on Ca3CoNb2O9. We find strong frustration and the existence of long-range order antiferromagnetism (LROAFM) at very low temperatures in this system.
We synthesized polycrystalline samples of Ca3CoNb2O9 by a standard solid state reaction method. CaCO3 (5-N Alfa), CoO (> 3-N Alfa), and Nb2O5 (4-N Alfa) powders with stoichiometric ratio were ground sufficiently and pressed into pellets. After sintering in air at 850 ° C for 10 hours, the pellets were then calcined at 1200 ° C for 72 hours with intermediate grinding and re-pelleting. The room temperature powder x-ray diffraction (XRD) measurement was performed on a Bruker XRD diffractometer with Cu Kα radiation. The susceptibility measurements in the temperature range 2 K– 300 K were performed with vibrating sample magnetometer (VSM) loaded on a physical property measurement system (Quantum Design PPMS). Magnetic measurements below 2 K were performed using a magnetic property measurement system (Quantum Design MPMS) with an 3He insert at McMaster University.
The XRD patterns of polycrystalline Ca3CoNb2O9 samples are presented in Fig. 2. Refinement of the observed diffraction peaks using the structure parameters obtained from previous neutron diffraction[17] gives a final weighted residual error Rwp = 2.64, which means that our XRD data match well with the calculated results. The obtained structure parameters a = 9.5988(9) Å , b = 5.4576(3) Å , and c = 16.8643(9) Å are also consistent with previous results.[17] No additional impurity peak is found in the whole diffraction range from 5° to 120° indicating that there is no obvious impurity phase in our samples.
The dc susceptibility and its inverse above 2 K under an external field of 0.1 T for Ca3CoNb2O9 are shown in Fig. 3.
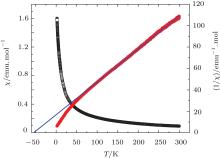 | Fig. 3. The dc susceptibility (χ = M/H) and its inverse measured at 0.1 T. The solid line is a linear Curie– Weiss fitting of χ in a temperature range 100 K– 300 K. |
It is shown from Fig. 3 that the 1/χ deviates from the Curie– Weiss curve at around 50 K. The susceptibility data above 100 K can be fit by the Curie– Weiss formula: χ M = C/(T − θ CW)+ χ 0, where C is the Curie constant, θ CW is the Weiss constant, and χ 0 is the temperature-independent paramagnetic susceptibility. The fitting gives an effective moment of 5.1 μ B and a Weiss constant of θ CW∼ − 55 K. Considering the contribution from the orbital angular momentum, the value of the moment is reasonable for the Co2+ ion in the highspin state.[18] The negative Weiss constant reflects dominant antiferromagnetic interactions between Co2+ ions. The large Weiss temperature and the absence of magnetic ordering down to 2 K imply the presence of strong frustration in this system.
To study the ground state magnetism of Ca3CoNb2O9, we performed susceptibility measurements down to 0.46 K with ZFC and FC methods. As shown in Fig. 4(a), under a 0.01-T external field, both ZFC and FC susceptibility increase with cooling. With further cooling, a cusp occurs at around 1.45 K, which indicates a transition from the paramagnetic phase to an ordered state. The susceptibility is less than 0.2- emu/mol Co2+ in the ordered state, which suggests a longrange order antiferromagnetism (LROAFM). Combined with the large Weiss constant obtained above, the frustration factor f (= | θ CW | /TN) is about 38, which is comparable to that of strong frustrated regular TLHAF Ba3CoNb2O9 (θ CW= − 51 K and TN1 = 1.36 K).[14] In contrast to the regular triangular lattice antiferromagnet Ba3CoNb2O9, Ca3CoNb2O9 has DM interactions and spatially anisotropic exchange interactions. Theoretical studies suggested that both interactions release frustration and enhance the LROAFM in general.[19, 20] For Ca3CoNb2O9, however, the anisotropy does not lift up magnetic ordering temperature significantly, which suggests that the DM interactions and spatial anisotropy are weak.
 | Fig. 4. (a)– (f) The dc susceptibility down to 0.46 K after ZFC and FC measured at external magnetic fields: 0.01 T, 0.1 T, 0.2 T, 0.5 T, 0.65 T, and 1 T, respectively. |
The magnetically ordered ground states were expected for the insulating triangular lattice antiferromagnets, including isotropic Heisenberg, [4] XXZ, [21] and distorted[11] models. Experimentally, almost all triangular antiferromagnets have been found with LROAFM at low temperatures, except κ -(BEDT-TTF)2Cu2(CN)3, which is probably closer to a Hubbard model.[22] Therefore, the LROAFM state is natural for our triangular lattice antiferromagnet.
At T ∼ 1.2 K, which is slightly below TN, deviation appears between the ZFC and FC data under 0.01-T field [Fig. 4(a)]. We further measure dc susceptibility after FC and ZFC at higher fields [see Figs. 4(b)– 4(f)]. Under a 0.1-T field, the FC susceptibility is suppressed slightly below TN, while the suppression effect is much stronger for the ZFC data, resulting in an enhancement of the deviation between the FC and ZFC data. With further increasing fields, the discrepancy is gradually suppressed monotonously and completely removed by a field of 1 T, while the position of TN remains at 1.45 K.
The deviation between ZFC and FC susceptibility data at low measurement fields was reported in some spin-canted antiferromagnets. For example, in DTLAFM Cu2(OH)3(CmH2m+ 1COO), m = 7, 9, 11, [23] the DM interactions were suggested to play an essential role to the spin canting. A similar situation may occur in Ca3CoNb2O9, where the DM interactions assist the canting of antiferromagnetic moments.
The bifurcation of ZFC and FC susceptibility was also seen in spin glass system with spin-freezing. Earlier theoretical studies suggested that the spin glass phase usually occurs in frustrated systems with quenched disorder.[24, 25] However, the spin glass can also be realized in the system with competing ferro- and antiferro-magnetic bonds distributed in a certain rule, rather than a random way.[26] Experimentally, the spin freezing transition has been found recently in several nominally disorder-free frustrated systems such as Y2Mo2O7, [27, 28] Gd3Ga5O12, [29] ZnCr2O4, [30] CsVCl3, [31] Cu2(OH)3(CmH2m+ 1COO), m = 7, 9, 11.[23] The spin glass and LROAFM phases coexist in the latter three materials. Whether disorder is essential to the generation of the spin glass in a strongly frustrated magnet remains to be established. Structurely, Ca3CoNb2O9 is a site-ordered system which has been confirmed by neutron diffraction experiment.[17] However, we cannot exclude the possibility of mixing tiny amounts of Nb5+ /Co2+ on the perovskite B-sites. It has been expected that the spin glass can be stabilized in geometrically frustrated antiferromagnets even with smallest degree of disorder.[32] After all, based on our current dc susceptibility data, we cannot exclusively determine the origin of observed deviation between the ZFC and FC susceptibility. Specific heat and ac susceptibility experiments down to 3He temperatures may help to resolve this issue.
To investigate the evolution of magnetism with external field in Ca3CoNb2O9, the dc magnetization was measured at 0.46 K [Fig. 5]. The magnetization increases linearly with field and then changes slope around 6 T, which corresponds to a crossover from a long-range ordered state to a fully polarized state, as in Ba3CoNb2O9.[14, 33] Above 6 T, though the magnetization still increases, it has a tendency to saturate around 2 μ B/Co2+ . Due to spin– orbital couplings and the crystal field, the ground state of Co2+ ion coordinated in octahedral environment is a Kramers doublet with an effective spin of 1/2.[34, 35] The low spin state of Co2+ has also been observed in many other TLAFM with octahedral Co sites, such as Ba3CoNb2O9, [14] Ba3CoSb2O9, [12] and CsCoCl3.[2] We further plot the first derivative of the magnetization curve as a function of field. Below 6 T, two valleys are observed in the derivative curve, which is reproducible on different samples. The first one located around 0.7 T, which is consistent with the field where the bifurcation between ZFC and FC susceptibility disappears [Fig. 4(b)– 4(f)]. The second one occurs at around 2.5 T with the magnetization of 0.75 μ B/Co2+ , which is close to 1/3 of the saturation magnetization (Ms). The possible appearance of a 1/3 magnetization plateau is consistent with the fact of strong quantum fluctuations from frustration and small effective spins in this triangular lattice.[7, 8] However, we are aware that the magnetization plateau is not strong, which may be because our samples are randomly aligned powders. Single crystal samples are needed to confirm this observation.
Our study revealed that the ground state for Ca3CoNb2O9 is a LROAFM coexisting with spin canting or spin glassiness. However, for a regular triangular lattice model, the ground state is coplanar 120° antiferromagnetic order, which has been confirmed in Ba3CoSb2O9, [12] Ba3NiNb2O9, [13] and Ba3CoNb2O9.[14] The different ground state of Ca3CoNb2O9 may be a result of the interplay of strong frustration and anisotropic interactions, and provides possibility of searching for new novel quantum states in this geometrically frustrated magnet. Moreover, the 1/3 plateau in magnetization for a DTLAF is a macroscopic manifestation of quantum effect predicted by theoretical studies.[11] To be more unique, this novel magnetic state can be stabilized by a very small field (2.5 T) which is easily accessible by experiments, and provides a promising material for further investigation of magnetization plateaus which are very interesting theoretically.
In conclusion, the magnetism of distorted triangular lattice antiferromagnet Ca3CoNb2O9 has been studied for the first time. The largeWeiss constant and very low ordering temperature imply strong geometrical frustration in Ca3CoNb2O9. Slightly below TN, a deviation between susceptibility data after ZFC and FC is observed below 0.7 T, which may be related to DM interactions and/or site disorder. A magnetic state with 1/3 of Ms is suggested in magnetization curve, which may be caused by strong quantum fluctuations in this triangular lattice. Ca3CoNb2O9 supplies a new system to study the magnetism of triangular lattice antiferromagnet with weak spatially anisotropic interactions and DM interactions.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|





