The crystal structure of CeFeSi and related compounds was first investigated by Bodak et al. in 1970, ^[18] and they found that these compounds crystallize in the tetragonal CeFeSi-type structure (space group P4/nmm). In 1992, Welter et al.^[19] studied the magnetic properties of RFeSi (R = La– Sm, Gd– Dy) compounds by susceptibility measurements and neutron diffraction studies. It was found that the RFeSi (R = Gd, Tb, and Dy) exhibit the FM state below their respective T_C. Later, Napoletano et al.^[20] reported that GdFeSi undergoes a FM-paramagnetic (PM) transition around 118  K and presents a large – Δ S_M of 22.3  J/kg· K and Δ T_ad of 4.5  K for a high field change of 9  T. Especially, it shows a giant refrigerant capacity (RC) value of 1940  J/kg in the 10  K– 160  K temperature range for a field change of 9  T. Recently, Zhang et al.^{[14, 21, 22]} investigated the magnetic properties and MCE of RFeSi (R = Gd– Er) compounds systematically. The maximum – Δ S_M values of GdFeSi are 6.0  J/kg· K and 11.3  J/kg· K for the field changes of 2  T and 5  T, respectively. In addition, the RC value, calculated by integrating numerically the area under the Δ S_M– T curve with defining the temperatures at half maximum of peak as the integration limits, ^[23] is obtained to be 373  J/kg for a field change of 5  T.

Figure  1 shows the temperature (T) dependence of zero-field-cooling (ZFC) and field-cooling (FC) magnetizations (M) under 0.05  T for RFeSi (R = Gd-Er) compounds.^{[14, 21, 22]} An obvious difference between ZFC and FC curves appears below the ordering temperature for RFeSi compounds except GdFeSi, which may be due to the domain-wall-pinning effect as usually observed in materials with low ordering temperature and high anisotropy.^{[14, 24]} The RFeSi (R = Tb and Dy) compounds experience a second-order FM– PM transition around the respective T_C of 110  K and 70  K for TbFeSi and DyFeSi, which are quite close to the liquefaction temperatures of natural gas (111  K) and nitrogen (77  K).^[21] In addition, an unusual discrepancy between ZFC and FC curves can be observed in PM state of RFeSi (R = Tb and Dy) compounds, suggesting the existence of short-range FM correlations just above T_C.^[25] The magnetic entropy change S_M of RFeSi (R = Tb and Dy) was calculated from the magnetization isotherms by using the Maxwell relation , ^[26] and the temperature dependence of Δ S_M for TbFeSi and DyFeSi under different magnetic field changes are shown in Fig.  2(a).^[21] It can be seen that TbFeSi and DyFeSi present large – Δ S_M values of 5.3  J/kg· K and 4.8  J/kg· K for a low field change of 1  T, respectively. This large MCE under a low field change is favorable to practical applications since the maximum field of permanent magnets in market is usually lower than 2  T. In addition, it is worth noting that the magnitude of MCE is nearly same for TbFeSi and DyFeSi. Therefore, a series of (Tb_{1− x}Dy_x)FeSi compounds can be predicted theoretically to exhibit continuous ordering temperatures with similar magnitude of MCE.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Temperature dependence of ZFC and FC magnetizations under 0.05  T for RFeSi (R = Gd– Er) compounds. The inset shows a close view of the M– T curves of TbFeSi and DyFeSi in the PM state.[14, 21, 22]

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Temperature dependence of Δ SM for RFeSi (R = Tb and Dy) under different magnetic field changes up to 5  T. (b) Temperature dependence of calculated Δ SM for (Tb1− xDyx)FeSi (x = 0– 1) compounds and the composite material under a magnetic field change of 1  T.[21]

Figure  2(b) shows the temperature dependence of calculated Δ S_M of (Tb_{1– x}Dy_x)FeSi compounds for a field change of 1  T.^[21] Furthermore, a composite material can be formed based on this series of (Tb_{1– x}Dy_x)FeSi compounds and the optimum mass ratio y_i of each component, determined by using a numerical method, ^[27] is as follows: y₁ = 19.43  wt%, y₂ = 13.32  wt%, y₃ = 13.47  wt%, y₄ = 13.74  wt%, y₅ = 15.08  wt%, and y₆ = 24.96  wt% for x = 0, 0.2, 0.4, 0.6, 0.8, and 1.0, respectively. The Δ S_M of this composite is estimated by using the equation and is shown in Fig.  2(b).^[21] The composite exhibits a constant – Δ S_com of ∼ 1.4  J/kg· K in a wide temperature range, thus resulting in a large RC of 64  J/kg for a field change of 1  T, which is 49% and 64 % higher than those of TbFeSi (43  J/kg) and DyFeSi (39  J/kg). Thermodynamic analysis indicates that a magnetic refrigeration system based on an ideal Ericsson cycle requires constant Δ S_M over a wide temperature range.^[1] Therefore, the above result suggests that the composite of (Tb_{1– x}Dy_x)FeSi can be a good candidate for magnetic refrigerants for the Ericsson cycle over the liquefaction temperatures of nitrogen and natural gas. Large reversible MCE for a relatively low magnetic field change has also been observed in ErFeSi compound.^[14]

Figure  3 shows the temperature dependence of Δ S_M and Δ T_ad of ErFeSi for different magnetic field changes.^[14] Here, the Δ T_ad was calculated from the heat capacity (C_P) curves by using the equation Δ T_ad (Δ H, T) = [T(S)_H − T(S)₀]_S. ^[26] For a magnetic field change of 5  T, the maximum values of – Δ S_M and Δ T_ad around the T_C = 22  K are 23.1  J/kg· K and 5.7  K, respectively. Particularly, the – Δ S_M and RC reach as high as 14.2  J/kg· K and 130  J/kg, respectively, for a relatively low field change of 2  T. This large MCE around liquid hydrogen temperature (20.3  K) indicates that ErFeSi could be a promising material for magnetic refrigeration of hydrogen liquefaction.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Temperature dependence of (a) Δ SM and (b) Δ Tad for ErFeSi under different magnetic field changes.[14]

Unlike other RFeSi compounds with FM ground state, HoFeSi exhibits a complex magnetic structure with FM and AFM/ferrimagnetic (FIM) moments at low temperatures. With the decrease of temperature, HoFeSi undergoes a PM– FM transition at T_C = 29  K. Besides, another anomaly is found at T_t = 20  K, which indicates that some magnetic moments in HoFeSi may experience an FM– AFM/FIM transition around T_t.^[22]

Figure  4(a) shows the magnetization isotherms of HoFeSi in the temperature range of 8  K– 24  K.^[22] It is seen that the magnetization below 20  K increases greatly at first with increasing magnetic field, corresponding to the typical FM behavior. A field-induced metamagnetic transition occurs at critical field with further increase of field, suggesting the possible presence of AFM or FIM components at low temperatures in HoFeSi compound. The fraction of FM components, estimated by extrapolating the plateau of FM state to 5  T, is about 79% at 8  K and reaches nearly 100% when temperature increases to 24  K (see inset of Fig.  4(a)). The temperature dependence of Δ S_M for HoFeSi under different magnetic field changes is shown in Fig.  4(b).^[22] It is noted that HoFeSi presents negative Δ S_M peak (normal MCE) around T_C as well as positive Δ S_M (inverse MCE) around T_t. For a relatively low field change of 2  T, the Δ S_M values are 5.6  J/kg· K at T_t and – 7.1  J/kg· K at T_C, respectively. This special feature of successive inverse and normal MCE in HoFeSi could be applied in some refrigerators with special designs and functions, which other materials with only normal MCE cannot satisfy.^[28]

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. (a) Magnetization isotherms of HoFeSi compound in the temperature range of 8  K– 24  K. The inset shows the fraction of FM phase as a function of temperature estimated from magnetization isotherms. (b) Temperature dependence of magnetic entropy change Δ SM for HoFeSi compound under different magnetic field changes up to 5  T.[22]

The crystal structures and magnetic properties of RCoSi compounds vary with the rare earth elements. Neutron diffraction studies reveal that RCoSi (R = Gd and Tb) crystallize in the tetragonal structure of CeFeSi-type (space group P4/nmm) and order antiferromagnetically below T_N of 175  K and 140  K for R = Gd and Tb, respectively.^[29] However, RCoSi (R = Dy, Ho, and Er) compounds have been reported to crystallize in the orthorhombic TiNiSi-type crystal structure and exhibit PM– FM transition at low temperatures.^{[30– 32]} Leciejewicz et al.^[31] investigated the magnetic structure of HoCoSi by neutron diffraction and found that the magnetic moments order ferromagnetically below T_C = 13  K. Besides, the magnetic moments of Ho atoms form a conical spiral at 1.7  K, leading to the coexistence of the collinear FM structure and helicoidal structure.

In 2012, Xu et al.^[32] further investigated the MCE of HoCoSi compound systematically by magnetization and heat capacity measurements. Figure  5 displays the heat capacity (C_P) curves for HoCoSi under different magnetic fields.^[32] A distinct λ -type peak is observed around 11.2  K in zero field, corresponding to the second-order FM– PM transition. In addition, another anomaly is observed at T_t = 4  K in the thermomagnetic curve (inset of Fig.  5), corresponding to the critical temperature of the coexistence of the collinear FM structure and helicoidal structure. With the increase of magnetic field, the peak gradually becomes broader and lower while it also moves to a slightly higher temperature, suggesting the typical characteristic of ferromagnet.^[1] Based on the theory of thermodynamics, the Δ S_M and Δ T_ad values can be calculated from the C_P curves by using the following equations and Δ T_ad (Δ H, T) = [T(S)_H − T(S)₀]_S, respectively. Figure  6 shows the temperature dependence of Δ S_M and Δ T_ad for HoCoSi under different magnetic field changes.^[32] It is found that the – Δ S_M and Δ T_ad reach as high as 26.3  J/kg· K and 11.0  K for a magnetic field change of 5  T. Moreover, for a relatively low field change of 2  T, HoCoSi compound exhibits a giant MCE around T_C = 15  K with the maximum – Δ S_M of 17.3  J/kg· K and T_ad of 6.2  K. Very recently, Gupta et al.^[33] also reported the MCE of HoCoSi compound and observed a large MCE without hysteresis loss around the T_C of 14  K. For a magnetic field change of 5  T, the maximum – Δ S_M and RC values of HoCoSi are 20.5  J/kg· K and 410  J/kg, respectively.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Heat capacity (CP) curves for HoCoSi under different magnetic fields. The inset shows the temperature dependence of ZFC and FC curves for HoCoSi under the magnetic field of 0.01  T.[32]

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Temperature dependence of (a) Δ SM and (b) Δ Tad for HoCoSi under different magnetic field changes.[32]

Xu et al.^[32] further studied the effect of Er substitution on the magnetic and magnetocaloric properties in (Ho_{1– x}Er_x)CoSi compounds. Figure  7 shows the temperature dependence of ZFC and FC magnetizations under 0.01  T for (Ho_{1– x}Er_x)CoSi compounds.^[32] In addition to the FM– PM transition around T_C, all (Ho_{1– x}Er_x)CoSi compounds except ErCoSi exhibit another anomaly at lower temperature T_t, which is related to the presence of magnetic helicoidal structure. It is clearly seen that the transition temperatures decrease linearly with the Er content increasing from 0 to 1 (inset of Fig.  7). Figure  8 shows the temperature dependence of Δ S_M for (Ho_{1– x}Er_x)CoSi compounds under a field change of 2  T.^[32] For a field change of 2  T, the maximum – Δ S_M values are 17.9, 17.9, 18.2, 18.0, 18.5, and 18.7  J/kg· K for x = 0, 0.2, 0.4, 0.6, 0.8, and 1, respectively. It can be seen that (Ho_{1– x}Er_x)CoSi compounds exhibit nearly the same magnitude of MCE with increasing Er content. Meanwhile, the T_C decreases from 15  K to 5.5  K with the variation of x from 0 to 1. Therefore, a composite material can be constructed based on this series of (Ho_{1– x}Er_x)CoSi compounds and exhibits a constant Δ S_M in the temperature range of 5.5  K– 15  K, satisfying the requirement of Ericsson-cycle magnetic refrigeration. Similar research has also been carried out in (Ho_{1– x}Dy_x)CoSi compounds.^[32] However, single phase with tetragonal CeFeSi-type structure can not be obtained when Dy content is higher than 0.4, due to the presence of DyCo₂Si₂ phase impurity. It is found that the T_C decreases from 15  K for x = 0 to 5  K for x = 0.4 in (Ho_{1– x}Dy_x)CoSi compounds.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Temperature dependence of ZFC and FC magnetizations under 0.01  T for (Ho1– xErx)CoSi compounds. The inset shows the transition temperatures as a function of as a function of x.[32]

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. The temperature dependence of Δ SM for (Ho1– xErx)CoSi compounds under a magnetic field change of 2  T.[32]

Figure  9 shows the temperature dependence of Δ S_M for Ho_0.8Dy_0.2CoSi compound under different magnetic field changes.^[32] For a magnetic field change of 5  T, Ho_0.8Dy_0.2CoSi exhibits a maximum – Δ S_M value of 20.2  J/kg· K around T_C = 12  K. The reduction of MCE is due to the fact that the introduction of Dy atoms would result in the competition of FM coupling of Ho moments and AFM coupling of Dy moments, thus lowering the saturation magnetization and MCE of (Ho_{1– x}Dy_x)CoSi compounds.

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. Temperature dependence of Δ SM for Ho0.8Dy0.2CoSi under different magnetic field changes.[32]

In 1974, Bodak et al.^[34] reported that all RNiSi (R = Gd– Lu) compounds crystallize in the orthorhombic TiNiSi-type crystal structure. In 1999, Szytula et al.^[35] further investigated the magnetic properties of RNiSi (R = Tb– Er) compounds by neutron diffraction and magnetometric measurement studies. It was found that all RNiSi (R = Tb– Er) compounds show AFM ordering with strong magnetocrystalline anisotropy at low temperatures. In addition, the neutron diffraction studies reveal that another ordering change of magnetic moments from sine to square-modulated structure occurs below T_N. Very recently, the MCE of RNiSi (R = Tb– Er) compounds have been investigated by different researchers.^{[36– 38]} Among these materials, HoNiSi exhibits the largest MCE due to the field-induced metamagnetic transition.^[36]

Zhang et al.^[37] recently reported giant rotating MCE in textured DyNiSi polycrystalline material that is larger than those of most rotating magnetic refrigerants reported so far. Figure  10 shows the temperature dependence of ZFC and FC magnetizations for DyNiSi at 0.05  T along the parallel and perpendicular directions, respectively.^[37] It is seen that both thermomagnetic curves show similar trend but with different magnetizations. With the decrease of temperature, DyNiSi undergoes a PM– AFM transition at T_N of 8.8  K. In addition, another anomaly is found around the transition temperature T_t = 4  K, which is likely attributable to the ordering change of magnetic moments from sine to square-modulated structure, based on neutron diffraction studies.^[35] The magnetization was measured by rotating the DyNiSi sample in the magnetic field of 0.05  T as shown in the inset of Fig.  10. Here, the rotation angle θ is defined as 0° when the longitudinal direction of columnar grains is parallel to the magnetic field. It can be clearly seen that the magnetization decreases gradually by rotating the sample from parallel to perpendicular direction, indicating that the easy magnetization axis is consistent with the preferred crystalline orientation.

Fig.  10.

	Figure Option ViewDownloadNew Window
	Fig.  10. Temperature dependence of ZFC and FC magnetizations for DyNiSi at 0.05  T along the parallel and perpendicular directions, respectively. The inset shows the magnetization as a function of rotation angle at 20  K under 0.05  T.[37]

Figures  11(a) and 11(b) show the temperature dependence of Δ S for DyNiSi for different magnetic field changes along parallel and perpendicular directions, respectively.^[37] It can be seen that DyNiSi exhibits a giant anisotropic MCE, e.g., the maximum − Δ S values are 22.9  J/kg· K and 5.9  J/kg· K for a field change of 5  T along parallel and perpendicular directions, respectively. A small negative − Δ S value (inverse MCE) is observed below T_N at 1  T along the parallel direction because of the presence of the AFM state, while it becomes positive with the increase of magnetic field. Such a sign change of − Δ S is due to the field-induced AFM– FM metamagnetic transition.^[39] In addition, another − Δ S peak is found around T_t for both directions. It is speculated that the transition from sine to square-modulated structure may lead to some unstable moments below T_t. Therefore, an applied magnetic field will turn these AFM components into FM ordering, which exhibits a magnetically more ordered configuration, and then result in a positive − Δ S peak. Figure  11(c) shows the difference of Δ S for DyNiSi between different directions as a function of temperature for different magnetic field changes.^[37] For the field changes of 2  T and 5  T, the − Δ S_diff peak reaches as high as 11.1  J/kg· K at 8.5  K and 17.6  J/kg· K at 13  K due to the giant anisotropy of MCE. This result indicates that a large rotating MCE can be obtained by rotating the sample from perpendicular to parallel.

Fig.  11.

	Figure Option ViewDownloadNew Window
	Fig.  11. Temperature dependence of Δ S for DyNiSi for different magnetic field changes along (a) parallel and (b) perpendicular directions, respectively. (c) The difference of Δ S for DyNiSi between different directions as a function of temperature for different magnetic field changes.[37]

Furthermore, the isothermal magnetization curves at 8  K and 9  K were measured for DyNiSi under applied fields up to 2  T by rotating the sample from perpendicular (90° ) to parallel (0° ) with a step of 10° as shown in the inset of Fig.  12.^[37] By defining the rotating entropy change Δ S^R(90° ) as zero, the Δ S^R(θ ) value at 8.5  K can be obtained based on the magnetization curves by using the following equation:

Fig.  12.

	Figure Option ViewDownloadNew Window
	Fig.  12. The Δ SR(θ ) of DyNiSi as a function of rotation angle for different magnetic field changes. The inset describes the rotation of sample from perpendicular (90° ) to parallel (0° ) direction in magnetic field.[37]

Figure  12 shows the Δ S^R(θ ) as a function of rotation angle for different magnetic field changes.^[37] It is noted that small negative − Δ S^R(θ ) value is observed under relatively low fields near the perpendicular direction. This can be understood that the disordering of magnetic moments in AFM sublattice is enhanced under low fields when the rotation just starts, and thus it leads to a positive entropy change. Further rotating the sample closer to parallel, the majority of spins in the AFM sublattice could orient along the field direction, which then increases the spin ordering and results in the positive − Δ S^R(θ ) value. Under the magnetic field of 2  T, the − Δ S^R(θ ) value increases gradually and reaches a maximum value of 7.9  J/kg· K as the sample is rotated from perpendicular to parallel.

Figures  13(a) and 13(b) show the temperature dependence of ZFC and FC magnetizations for HoNiSi^[36] and ErNiSi under 0.05  T. It is seen that HoNiSi and ErNiSi undergo an AFM– PM transition around the Né el temperature T_N = 3.8  K and 4  K, respectively, which are just around the critical temperature of liquid helium (4  K), suggesting the potential application of RNiSi (R = Ho and Er) for helium liquefaction. Besides, no obvious discrepancy between ZFC and FC curves is observed, indicating good thermomagnetic reversibility of the magnetic transition. The temperature dependence of magnetization in various magnetic fields is shown in the inset of Figs.  13(a) and 13(b). It can be seen that RNiSi (R = Ho and Er) exhibit typical AFM– PM transition under low fields. However, the magnetization at low temperatures increases greatly with increasing field, revealing the occurrence of a field-induced AFM– FM metamagnetic transition below T_N. In addition, a step-like behavior of M– T curves above T_N is also observed when field is larger than 0.3  T for HoNiSi and 0.7  T for ErNiSi, respectively, corresponding to the FM– PM transition.^[40]

Fig.  13.

	Figure Option ViewDownloadNew Window
	Fig.  13. Temperature dependence of ZFC and FC magnetizations for (a) HoNiSi[36] and (b) ErNiSi under 0.05  T. Inset shows the temperature dependence of magnetization in various magnetic fields for HoNiSi[36] and ErNiSi, respectively.

Figures  14(a) and 14(b) show the temperature dependence of Δ S_M for HoNiSi^[36] and ErNiSi under different magnetic field changes up to 5  T. It is well known that the Δ S_M values can be calculated either from the magnetization isotherms by using the Maxwell relation or from the heat capacity by using the equation , ^[26] respectively. However, sometimes the values of Δ S_M calculated from heat capacity may be much lower than those obtained from magnetization isotherms, which is likely due to either an erroneous calculation of the Maxwell relation in the vicinity of FOPT or poor contact between the sample and the measuring platform during heat capacity measurement.^{[14, 41]} For comparison, the Δ S_M values were estimated from both methods as shown in Fig.  14(a), and it can be clearly seen that the Δ S_M curves obtained from two methods match well with each other. For a field change of 2  T, the maximum – Δ S_M values for HoNiSi and ErNiSi around T_N are 17.5  J/kg· K and 8.8  J/kg· K, respectively. Besides, a large positive Δ S_M (inverse MCE) can be observed below T_N, which is caused by the presence of AFM ordering at low temperatures. For example, the Δ S_M of HoNiSi below T_N reaches 7.2  J/kg· K for a low field change of 0.5  T, and the maximum Δ S_M of ErNiSi below T_N is 6.5  J/kg· K for a low field change of 1  T. These large normal and inverse MCE under low field change indicate that RNiSi (R = Ho and Er) could be applied in magnetic refrigeration with either adiabatic magnetization or adiabatic demagnetization.

Fig.  14.

	Figure Option ViewDownloadNew Window
	Fig.  14. Temperature dependence of Δ SM for (a) HoNiSi[36] and (b) ErNiSi under different magnetic field changes up to 5  T. The Δ SM of HoNiSi was calculated from magnetizations (open symbols) and heat capacity measurements (full symbols). Inset shows the universal curve of Δ SM for HoNiSi compound under various magnetic field changes.

Recently, Franco et al.^{[42, 43]} proposed a phenomenological procedure to construct the universal curve of Δ S_M for materials with second-order FM– PM transition. However, the applicability of this universal curve has not been proven for AFM materials. As shown in the inset of Fig.  14(a), Zhang et al.^[36] were first to construct the universal curve of Δ S_M for HoNiSi by using this phenomenological procedure. The normalized Δ S′ is defined as . The temperature axis has been rescaled in a different way below and above T_pk, by imposing that the positions of two reference points in the curve correspond to θ = ± 1,

where T_r1 and T_r2 are the temperatures of the two reference points which correspond to . All the curves under different field changes collapse onto the same universal curve, though the ground state changes from AFM to FM with the increase of magnetic field. This result reveals that the universal Δ S_M curve could also be applied in AFM or at least weak AFM materials.

Figure  15 displays the temperature dependence of Δ T_ad for HoNiSi under different magnetic field changes.^[36] HoNiSi exhibits large Δ T_ad values of 4.5  K and 8.5  K for the field changes of 2  T and 5  T, respectively, which is attributed to the field-induced metamagnetic transition from weak AFM to FM states.^[15] In addition, it is found that both Δ S_M and Δ T_ad peaks for HoNiSi compound broaden asymmetrically towards high temperatures with increasing field, indicating the presence of FM ordering above T_N induced by magnetic field.^[44] Moreover, this broad distribution of Δ S_M peak of HoNiSi leads to a high RC value of 471  J/kg for a field change of 5  T.

Fig.  15.

	Figure Option ViewDownloadNew Window
	Fig.  15. Temperature dependence of Δ Tad for HoNiSi under different magnetic field changes.[36]

The series of ternary intermetallic RCuSi compounds have been investigated extensively in the past few decades due to the interesting physical properties. It has been reported that these compounds crystallize within two types of crystal structure depending on the annealing temperature. The high-temperature phase crystallizes in the AlB₂-type structure (space group P6/mmm) with R atoms at 1a: (0, 0, 0) and Cu/Si atoms statistically at 2d: (1/3, 2/3, 1/2).^[45] The low-temperature phase adopts the Ni₂In-type structure (space group P6₃/mmc) with R at 2a: (0, 0, 0), Cu at 2c: (1/3, 2/3, 1/4), and Si at 2d: (1/3, 2/3, 3/4), respectively.^{[46, 47]} The magnetic properties of RCuSi vary greatly with the change of crystal structure and rare earth element. According to the magnetic susceptibility measurements, Kido et al.^[48] suggested that the AlB₂-type RCuSi compounds with R = Ce, Nd order antiferromagnetically while those with R = Gd, Ho order ferromagnetically. As for the RCuSi compounds with Ni₂In-type structure, neutron diffraction studies reveal that RCuSi compounds with R = Tb, Dy, Ho, and Er orders antiferromagnetically below T_N = 16  K, 11  K, 9  K, and 6.8  K respectively.^{[49– 52]}

In 2010, Chen et al.^{[15, 53, 54]} investigated systematically the magnetic properties and MCE of RCuSi (R = Gd– Er) with Ni₂In-type structure. It was found that these compounds show weak AFM ground state at low temperatures, which could be easily induced into FM state by magnetic field, and thus lead to large MCE. Figure  16 shows the temperature dependence of ZFC and FC magnetizations under the magnetic field of 0.01  T for RCuSi (R = Gd, Tb, Dy, and Er) compounds.^[54] It can be found that the RCuSi compounds undergo an AFM– PM transition at T_N = 14, 11, 10, and 7  K for R = Gd, Tb, Dy, and Er, respectively. The ZFC and FC curves are completely reversible above T_N, suggesting good thermomagnetic reversibility of the magnetic transition. However, a small discrepancy is observed below T_N, which is likely related to the domain-wall-pinning effect. In ZFC mode, the domain walls are pinned and the thermal energy is not strong enough to overcome the energy barriers, and this leads to the low magnetization at low temperatures. However, in FC mode, the magnetic field during the cooling prevents the pinning effect and therefore, the magnetization at low temperatures is higher than that in ZFC mode. Figure  17 shows the temperature dependence of Δ S_M for RCuSi (R = Gd, Tb, Dy, and Er) compounds under different magnetic field changes.^[54] It is clearly seen that that RCuSi (R = Gd, and Tb) compounds exhibit a small negative Δ S_M value at a lower temperature, but the Δ S_M changes to positive value with increasing magnetic field, corresponding to the field-induced metamagnetic transition from AFM to FM states. This sign change of Δ S_M is not observed in DyCuSi and ErCuSi, indicating that the weak AFM coupling in RCuSi (R = Dy and Er) could be easily induced into FM state under lower field. Moreover, a large MCE can be obtained due to the field-induced metamagnetic transition. For a magnetic field change of 5  T, the maximum – Δ S_M values are 9.2, 10.0, 24.0, and 23.1  J/kg· K for R = Gd, Tb, Dy, and Er, respectively.

Fig.  16.

	Figure Option ViewDownloadNew Window
	Fig.  16. Temperature dependence of ZFC and FC magnetizations under the magnetic field of 0.01  T for RCuSi (R = Gd, Tb, Dy, and Er) compounds.[54]

Fig.  17.

	Figure Option ViewDownloadNew Window
	Fig.  17. Temperature dependence of Δ SM for RCuSi (R = Gd, Tb, Dy, and Er) compounds under different magnetic field changes.[54]

Figure  18 shows the temperature dependence of magnetization for HoCuSi under various magnetic fields.^[15] It is seen that HoCuSi undergoes an AFM to PM transition around T_N of 7  K under low fields. With the increase of magnetic field, the magnetization at low temperatures increases greatly, indicating the occurrence of a field-induced metamagnetic transition from AFM to FM states. In addition, a stepwise behavior of the M– T curves above T_N is observed when the field is higher than 0.3  T, corresponding to the FM– PM transition. The Δ S_M of HoCuSi as a function of temperature for different magnetic field changes is shown in Fig.  19.^[15] The maximum – Δ S_M and RC values are obtained to be 33.1  J/kg· K and 385  J/kg, respectively for a magnetic field change of 5  T, which are comparable with or even higher than those of other refrigerant materials in a similar temperature range. Particularly, the – Δ S_M reaches as high as 16.7  J/kg· K for a relatively low field change of 2  T, making HoCuSi attractive candidate for magnetic refrigeration materials in the low temperature range.

Fig.  18.

	Figure Option ViewDownloadNew Window
	Fig.  18. Temperature dependence of magnetization for HoCuSi under various magnetic fields.[15]

Fig.  19.

	Figure Option ViewDownloadNew Window
	Fig.  19. The Δ SM of HoCuSi as a function of temperature for different magnetic field changes.[15]

The large MCE in HoCuSi compound is mainly attributed to the following reasons: (i) the high saturation magnetization (M_S∼ 9.47∼ μ _B), ^[15] (ii) the field-induced metamagnetic transition from AFM to FM states, ^[55] and (iii) the large change in lattice volume around T_N.^[51] In order to investigate the change of lattice volume, the thermal expansion data (Δ L/L_{(50  K)}) under different fields has been measured by the means of strain gauge method^[56] and is shown in Fig.  20.^[54] The (Δ L/L_{(50  K)}) value decreases linearly with decreasing temperature above T_N but drops abruptly around T_N in zero magnetic field. This result confirms the occurrence of abrupt thermal expansion around T_N, which is caused by the change of lattice constants. In addition, it is noted that the abrupt thermal expansion shifts to higher temperature with the increase of field, leading to the asymmetrical broadening of the – Δ S_M peak.

Fig.  20.

	Figure Option ViewDownloadNew Window
	Fig.  20. Temperature dependence of thermal expansion data (Δ L/L(50  K)) under different fields for HoCuSi.[54]

It has been reported that all RFeAl (R = Gd– Dy) compounds crystallize in the hexagonal MgZn₂-type structure (space group P6₃/mmc) when quenched after annealing.^{[57– 60]} However, Klimczak et al.^[57] found that GdFeAl crystallizes in cubic MgCu₂-type structure (space group Fd3m) when cooled slowly, which exhibits lower saturation magnetic moments than that of GdFeAl with MgZn₂-type structure. In 1973, Oesterreicher et al.^[61] reported that both GdFeAl and TbFeAl with MgZn₂-type structure order ferrimagnetically below the transition temperatures of 260  K and 195  K, respectively. In addition, an S-shape of the M– H curve is observed in TbFeAl compound at low temperatures, which was ascribed to the partial chemical disorder of Fe and Al atoms as well as high magnetocrystalline anisotropy.^{[61, 62]} Similar results have also been observed by Kastil et al.^[59] In recent years, the MCE of RFeAl (R = Gd– Dy) have been reported by different researchers, and it is found that these compounds show reversible MCE in a wide temperature range, leading to a high RC value.^{[58– 60]}

In 2009, Dong et al.^[58] were first to investigate the MCE of GdFeAl compound with MgZn₂-type structure. Figure  21(a) shows the temperature dependence of magnetization for GdFeAl under 0.1  T.^[58] The transition temperature T_C is 265  K, defined as the minimum value of dM/dT curve. This T_C is close to room temperature, indicating the possible application of GdFeAl compound for magnetic refrigeration near room temperature. The isothermal magnetization at 5  K is presented in Fig.  21(b).^[58] The saturation magnetization μ _S is determined to be 5.8  μ _B per formula, which is lower than the theoretical gJ value of 7  μ _B for a free Gd³⁺ ion. This lower value of μ _S is attributed to the AFM coupling between the magnetic moments of Gd and Fe sublattices.^[63]

Fig.  21.

	Figure Option ViewDownloadNew Window
	Fig.  21. (a) Temperature dependence of magnetization for GdFeAl under a field of 0.1  T. (b) The magnetization curve at 5  K for GdFeAl compound.[58]

Figure  22 displays the temperature dependence of Δ S_M for GdFeAl under the magnetic field changes of 2  T and 5  T, respectively.^[58] The maximum – Δ S_M value is 3.7  J/kg· K for a field change of 5  T, which is lower than those of most magnetic refrigerants in the same temperature range. However, the Δ S_M peak spreads out over a wide temperature range and the full width at half maximum of the peak is 159  K. This broad distribution of Δ S_M peak results in a high RC value of 420  J/kg for a field change of 5  T. In addition, a perfect magnetic reversibility around the transition temperature is observed in the M– H curves with the field increasing and decreasing modes, corresponding to the typical second-order magnetic transition. This result indicates that the detrimental effects for fast-cycling refrigerators of hysteresis losses and slow kinetics do not exist in GdFeAl. Very recently, Kastil et al.^[59] also studied the MCE of RFeAl (R = Gd, Tb) and observed large relative cooling power (RCP) of 348  J/kg and 350  J/kg over a wide temperature region for GdFeAl and TbFeAl, respectively. Li et al.^{[60, 64]} reported the MCE of RFeAl (R = Dy, Ho, and Er) and found that the RC of DyFeAl reaches the largest value of 832  J/kg for a field change of 7  T in this series of compounds.

Fig.  22.

	Figure Option ViewDownloadNew Window
	Fig.  22. Temperature dependence of Δ SM for GdFeAl under the magnetic field changes of 2  T and 5  T, respectively.[58]

RCoAl compounds have been reported to crystallize in the hexagonal MgZn₂-type structure (space group P6₃/mmc) which is a close-packed Laves phase.^[65] In 2000, Jarosz et al.^[66] investigated the crystallographic, electronic structure and magnetic properties of GdCoAl compound systematically, and reported that GdCoAl undergoes a typical FM– PM transition at T_C = 100  K. Later, Zhang et al.^[67] studied the magnetic entropy change of RCoAl (R = Gd - Ho) compounds in the temperature range of 10  K– 100  K. Figure  23 presents the T_C and Δ S_M for a field change of 5  T as a function of R atom type. It is found that the T_C decreases linearly with the rare earth atom varying from Gd to Tm. In contrast, the Δ S_M has been reported to increase with the R atom changing from Gd to Tm. For a field change of 5  T, the HoCoAl exhibits the largest – Δ S_M of 21.5  J/kg· K around T_C = 10  K. In addition, a table-like Δ S_M peak was observed over the temperature range of 70  K– 105  K in GdCoAl compound. Although the – Δ S_M of 10.4  J/kg· K is relatively low for GdCoAl, this flat Δ S_M peak over a wide temperature range satisfies the requirement of a magnetic refrigerator based on an ideal Ericsson cycle, and also makes GdCoAl an attractive candidate material to fill the gap near 100  K in the Δ S_M– T profile required by an eight-stage magnetic refrigerator.^[68] In 2010, Chelvane et al.^[69] also investigated the magnetic and magnetocaloric properties of DyCoAl compound by magnetization and neutron diffraction measurements. It was found that DyCoAl has a collinear ferromagnetic structure where Dy moments lie in the ab plane at 10  K. A reversible MCE with – Δ S_M of 18  J/kg· K for a field change of 9  T is obtained in DyCoAl around 37  K.

Fig.  23.

	Figure Option ViewDownloadNew Window
	Fig.  23. The TC and SM for a field change of 5  T as a function of R atom for RCoAl compounds.

Very recently, Mo et al.^[70] further studied the MCE of TmCoAl. Figure  24(a) shows the temperature dependence of magnetization under the magnetic field of 0.01  T for TmCoAl.^[70] It can be found that TmCoAl undergoes a typical second-order magnetic transition from FM to PM states around T_C = 6  K, which is just above the boiling temperature of helium. A significant thermomagnetic irreversibility can be clearly seen below T_C, which likely arises from the narrow domain-wall-pinning effect. The inverse dc susceptibility (χ ^{− 1}) under 0.01  T and the Curie– Weiss fit to the experimental data for TmCoAl are plotted in the Fig.  24(b).^[70] The inverse susceptibility above T_C obeys the Curie– Weiss law χ ^{– 1} = (T− θ _P)/C, where θ _P is the paramagnetic Curie temperature and C is the Curie– Weiss constant. Based on the calculation of Curie– Weiss fit, the values of θ _P and effective magnetic moment (μ _eff) for TmCoAl are obtained to be 4  K and 5.93  μ _B/Tm³⁺ , respectively. The μ _eff value is lower than the theoretical magnetic moment of Tm³⁺ free ion, which is likely due to the crystal field effects and magnetic anisotropy. Figure  25 shows the temperature dependence of Δ S_M for TmCoAl under different magnetic field changes.^[70] It is seen that TmCoAl exhibits a large – Δ S_M value of 10.2  J/kg· K for a low magnetic field change of 2  T, comparable with or larger than those of most potential magnetic refrigerants with a similar magnetic transition temperature. Moreover, no thermal and magnetic hysteresis loss has been observed in TmCoAl. Therefore, the large reversible MCE suggests that TmCoAl could be a promising candidate for a magnetic refrigeration at low temperatures.

Fig.  24.

	Figure Option ViewDownloadNew Window
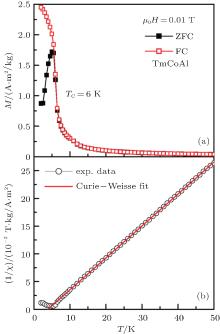	Fig.  24. (a) Temperature dependence of ZFC and FC magnetizations for TmCoAl compound under the magnetic field of 0.01  T. (b) Temperature variation of the inverse dc susceptibility fitted to the Curie– Weiss law for TmCoAl.[70]

Fig.  25.

	Figure Option ViewDownloadNew Window
	Fig.  25. Temperature dependence of Δ SM for TmCoAl under different magnetic field changes.[70]

The RNiAl alloys have been intensively studied for their complex magnetic structures and related interesting physical properties.^{[66, 71– 74]} All RNiAl compounds crystallize in the ZrNiAl-type hexagonal structure (space group ). Neutron diffraction experiments revealed the coexistence of FM and AFM states in isostructural RNiAl compounds (R = Tb, Dy, and Ho) compounds.^{[71, 75, 76]} Korte et al.^[72] reported that GdNiAl compound experiences three transitions with FM ordering of the Gd spins at T_C = 58  K accompanied by AFM processes at T₁ = 28  K and T₂ = 23  K, respectively. A similar result has also been observed by Si et al. in the study of annealed GdNiAl ribbon.^[74] The successive magnetic transitions lead to a broad Δ S_M peak over a wide temperature range. By substituting Gd with Er, all transition temperatures shift to lower temperature while the MCE increases gradually. Singh et al.^{[77– 79]} investigated the magnetic and magnetocaloric properties of RNiAl (R = Tb, Dy, and Ho) in detail, and found that these compounds undergo two successive transitions with the decrease of temperature. For example, HoNiAl experiences an PM– FM transition at T_C = 14  K followed by a FM– AFM transition at T₁ = 5  K, and exhibits a large – Δ S_M of 12.3  J/kg· K around T_C for a field change of 2  T.^[79] Mo et al.^[80] further reported that TmNiAl orders antiferromagnetically below 4  K, and shows a maximum – Δ S_M of 12.7  J/kg· K for a field change of 5  T due to the metamagnetic transition from AFM to FM states.

In order to investigate the effect of Cu doping on the magnetic and magnetocaloric properties in the TmNiAl compound, Mo et al.^[81] also studied the TmNi_{1– x}Cu_xAl compounds. Figure  26 displays the isothermal magnetization curves of TmNi_{1– x}Cu_xAl compounds as a function of magnetic field measured at 2  K in applied fields up to 5  T.^[81] The magnetization increases linearly with increasing magnetic field in low-field ranges when x < 0.3, suggesting the existence of AFM ground state, and then exhibits a sharp increase at a critical field, confirming the field-induced metamagnetic transition from AFM to FM states. However, with increasing Cu-concentration in the x ≥ 0.3, the magnetization increases rapidly with magnetic field and tends to be saturated at 5  T, which corresponds to the typical FM nature. The variation of ground state is attributed to the rotation of Tm magnetic moments from basal plane to c axis, and thus leading to the canted AFM structure with larger projected moments along the c axis near T_ord. Meanwhile, the T_ord decreases from 4  K for x = 0 to 2.8  K for x = 1. Figure  27 shows the Δ S_M as a function of temperature for TmNi_{1– x}Cu_xAl compounds under a magnetic field change of 2  T.^[81] It is found that the – Δ S_M value increases largely with the increase of Cu content, e.g., the – Δ S_M value of 10.7  J/kg· K for TmNi₀.7Cu₀.3Al compound is almost twice that of TmNiAl compound (5.5  J/kg· K). The MCE of TmNi_{1– x}Cu_xAl compounds with x ≥ 0.3 are much higher than those of many magnetic refrigerant materials with a similar transition temperature.

Fig.  26.

	Figure Option ViewDownloadNew Window
	Fig.  26. Isothermal magnetization curves of TmNi1– xCuxAl compounds as a function of magnetic field measured at 2  K in applied fields up to 5  T.[81]

Fig.  27.

	Figure Option ViewDownloadNew Window
	Fig.  27. The Δ SM as a function of temperature for TmNi1– xCuxAl compounds under a magnetic field change of 2  T.[81]

In 2015, Cui et al.^[82] reported the magnetic properties and MCE in HoNi_{1– x}Cu_xAl compounds. The temperature dependence of magnetization for HoNi_{1– x}Cu_xAl compounds under the magnetic field of 0.01  T is displayed in Fig.  28. The HoNi_{1– x}Cu_xAl compounds with x ≤ 0.1 exhibit two magnetic transitions, which are speculated to be a PM– FM + AFM transition followed by an AFM– AFM transition. These complex magnetic transitions are induced by the combination and competition between FM and AFM orderings. Increasing Cu content further, the compounds with x = 0.2– 0.7 undergo a single AFM– PM transition, and the ones with x = 0.8∼ 1 are found to show a FM ground state at low temperatures. For comparison, Figure  29 shows the Δ S_M as a function of temperature for HoNi_{1– x}Cu_xAl with x = 0.3 and 0.8 under different magnetic field changes.^[82] A small negative value of – Δ S_M was observed for a low magnetic field change of 1  T in x = 0.3 compound, corresponding to the presence of AFM state at low temperatures. In contrast, the compound with x = 0.8 exhibits positive – Δ S_M for all magnetic field changes, which is due to the typical FM– PM transition. Large – Δ S_M values of 12.3  J/kg· K and 9.4  J/kg· K for a low field change of 2  T are obtained in HoNi_{1– x}Cu_xAl with x = 0.3 and 0.8, respectively.

Fig.  28.

	Figure Option ViewDownloadNew Window
	Fig.  28. Temperature dependence of magnetization for HoNi1– xCuxAl compounds under the magnetic field of 0.01  T.[82]

Fig.  29.

	Figure Option ViewDownloadNew Window
	Fig.  29. Temperature dependence of SM for HoNi1– xCuxAl with x = (a) 0.3 and (b) 0.8 under different magnetic field changes.[82]

Wang et al.^{[83, 84]} also reported similar work on ErNi_{1– x}Cu_xAl compounds. Figure  30 shows the temperature dependence of magnetization for ErNi_{1– x}Cu_xAl compounds with x = 0.2, 0.5, and 0.8, respectively.^[83] It is found that the sample with x = 0.2 orders antiferromagnetically below the T_N = 4.6  K, while the one with x = 0.5 orders ferromagnetically around the T_C = 5.8  K. A quasi Curie-like magnetic transition is observed at T_trs = 5.5  K for the x = 0.8 sample. In order to further investigate the nature of this magnetic transition, the ac susceptibilities in different frequencies for the samples with x = 0.5 and 0.8 were measured and plotted in Fig.  31.^[83] It is clearly seen that the peak position of ac susceptibilities for x = 0.5 is independent of frequency. On the contrary, the peak for x = 0.8 shifts toward higher temperatures with increasing the frequency as shown in the inset of Fig.  31(b), which suggests the possible existence of short-range order. Figure  32 shows temperature dependence of – Δ S_M under different magnetic field changes for ErNi_{1– x}Cu_xAl with x = 0.2, 0.5, and 0.8, respectively.^[83] The sample with x = 0.2 presents a small negative value of – Δ S_M below T_N under a low magnetic field change of 1  T, corresponding to the nature of AFM state at low temperatures. With the increase of magnetic field, the field-induced metamagnetic transition leads to a large positive – Δ S_M for compound with x = 0.2. For a relatively low field change of 2  T, the maximum – Δ S_M values are 10.1, 14.7, and 15.7  J/kg· K for x = 0.2, 0.5, and 0.8, respectively, and this large MCE under low field change is favorable for practical applications.

Fig.  30.

	Figure Option ViewDownloadNew Window
	Fig.  30. Temperature dependence of magnetization for ErNi1– xCuxAl compounds with x = 0.2, 0.5, and 0.8, respectively.[83]

Fig.  31.

	Figure Option ViewDownloadNew Window
	Fig.  31. Temperature dependences of real part of ac magnetic susceptibility for (a) x = 0.5 and (b) x = 0.8 samples, respectively. The inset shows the corresponding enlarged part of peak position at different frequencies for x = 0.8 sample.[83]

Fig.  32.

	Figure Option ViewDownloadNew Window
	Fig.  32. Temperature dependence of Δ SM under different magnetic field changes for ErNi1– xCuxAl with x = 0.2, 0.5, and 0.8, respectively.[83]

The RCuAl compounds, like RNiAl compounds, crystallize in the ZrNiAl-type hexagonal structure (space group ).^{[66, 85, 86]} However, unlike RNiAl compounds, all heavy rare-earth RCuAl compounds exhibit an FM ground state.^[87] There are two types of basal plane layers distributed along the c axis: one contains all the R atoms and one-third of Cu atoms, and the other contains a nonmagnetic layer formed by all the Al atoms and two-third of Cu atoms. This layered character of the crystalline structure leads to large uniaxial magnetic anisotropies in GdCuAl, DyCuAl, and ErCuAl, and a basal-plane type of magnetic anisotropy in HoCuAl.^[88]

Recently, Dong et al.^{[85, 86, 89– 91]} studied the MCE of RCuAl compounds systematically. Figure  33 shows the temperature dependence of ZFC and FC magnetizations for crystalline RCuAl (R = Gd– Er) compounds under 0.1  T and 0.05  T. These compounds undergo a typical FM– PM transition, and the T_C decreases monotonically with the R atom-type varying from Gd to Er as usually seen in other RTX compounds. Figure  34 displays the temperature dependence of Δ S_M for crystalline RCuAl (R = Gd– Er) compounds under a magnetic field change of 5  T. It can be seen that the Δ S_M value increases gradually with the R atom changing from Gd to Er, and reaches the maximum as high as 23.9  J/kg· K for HoCuAl. The large MCE of RCuAl (R = Gd– Er) compounds suggests them as promising candidates of magnetocaloric materials in the low temperature range. In addition, Dong et al.^{[89, 90]} compared the magnetic and magnetocaloric properties of amorphous and crystalline RCuAl (R = Gd, Tb) alloys. Figure  35 shows the temperature dependence of magnetization for (a) amorphous and (b) crystalline TbCuAl alloy under 0.1  T.^[90] The crystalline TbCuAl undergoes an FM– PM transition at T_C = 52  K while the amorphous counterpart shows a small cusp centered at 20  K, which is attributed to a spin-glass transition. Different MCE was also observed in the amorphous and crystalline TbCuAl alloys due to the different nature of magnetic transitions. As shown in Fig.  36, ^[90] the maximum – Δ S_M value is obtained to be 4.5  J/kg· K around 36  K under a field change of 5  T for amorphous TbCuAl alloy. However, – Δ S_M peak reaches 14.4  J/kg· K around 52  K under the same field change for crystalline TbCuAl alloy, which is much larger than that of amorphous alloy.

Fig.  33.

	Figure Option ViewDownloadNew Window
	Fig.  33. Temperature dependence of ZFC and FC magnetizations for crystalline RCuAl (R = Gd– Er) compounds under 0.1 and 0.05  T.[85, 86, 89, 90]

Fig.  34.

	Figure Option ViewDownloadNew Window
	Fig.  34. Temperature dependence of Δ SM for crystalline RCuAl (R = Gd– Er) compounds under a magnetic field change of 5  T.[85, 86, 89, 90]

Fig.  35.

	Figure Option ViewDownloadNew Window
	Fig.  35. The temperature dependence of magnetization for (a) amorphous and (b) crystalline TbCuAl alloys under 0.1  T.[90]

Fig.  36.

	Figure Option ViewDownloadNew Window
	Fig.  36. Temperature dependence of Δ SM for amorphous and crystalline TbCuAl alloys under different magnetic field changes.[90]

Since Dong et al.^[86] did not obtain the pure HoCuAl compound, and therefore, the existence of impurity phase may influence the MCE. Later, Wang et al.^[91] successfully synthesized pure HoCuAl compound and studied the magnetic properties and MCE in detail. Figure  37(a) shows the temperature dependence of magnetization for HoCuAl compound under 0.01  T.^[91] The HoCuAl experiences an FM to PM transition around T_C = 11.2  K, which is consistent with the data from an impure sample (12  K).^[86] The ZFC and FC curves show a distinct discrepancy below T_C as often observed in other RTX compounds. Taking into account the magnetic anisotropy and low T_C for HoCuAl, this thermomagnetic irreversibility is likely attributable to the domain-wall-pinning effect. Figure  37(b) shows the Δ S_M as a function of temperature for HoCuAl under different magnetic field changes.^[91] For a relatively low field change of 2  T, the maximum – Δ S_M value for the pure HoCuAl compound is as high as 17.5  J/kg· K at T_C = 11.2  K, which is 25% higher than that of an impure sample (14.0  J/kg· K). This large – Δ S_M is also deemed as the highest – Δ S_M value in RTAl (R = Gd– Tm) system reported so far.

Fig.  37.

	Figure Option ViewDownloadNew Window
	Fig.  37. (a) Temperature dependence of magnetization for HoCuAl compound under 0.01  T. (b) The SM as a function of temperature for HoCuAl under different magnetic field changes.[91]

In 2013, Mo et al.^[16] reported a low-field induced giant MCE in TmCuAl compound. With the decrease of temperature, TmCuAl exhibits a transition from PM to FM state at T_C = 2.8  K, which likely corresponds to the presence of a longitudinal spin wave magnetic structure according to the neutron diffraction studies.^[92] Figure  38 displays the temperature dependence of – Δ S_M and Δ T_ad for TmCuAl under different magnetic field changes.^[16] Large reversible MCE under low field change can be observed around the T_C, e.g., the – Δ S_M and Δ T_ad values of TmCuAl are 17.2  J/kg· K and 4.6  K for a field change of 2  T, respectively. Particularly, the – Δ S_M reaches as high as 12.2  J/kg· K for a low field change of 1  T, which can be applied by a permanent magnet. This giant MCE without thermal and magnetic hysteresis indicates that TmCuAl could be an attractive magnetic refrigerant around the helium liquefaction temperature.

Fig.  38.

	Figure Option ViewDownloadNew Window
	Fig.  38. Temperature dependence of (a) Δ SM and (b) Δ Tad for TmCuAl under different magnetic field changes.[16]

It has been found that different crystal structures can be formed in RPdAl compounds depending on the variation of heat treatment technique. RPdAl compounds crystallize in a hexagonal ZrNiAl-type structure as metastable high-temperature modification (HTM) through a high-temperature (∼ 1050  ° C) annealing and rapid cooling process, while they crystallize in an orthorhombic TiNiSi-type structure as stable low-temperature modification (LTM) by a low-temperature (∼ 750  ° C) annealing process.^[93] In addition, an isostructural phase transition from a high-temperature HTM  I phase to a low-temperature HTM  II phase was observed in GdPdAl and TbPdAl with a metastable HTM.^{[94, 95]}

The RPdAl (R = Gd, Tb, Dy) compounds with the hexagonal ZrNiAl-type HTM were reported to exhibit two magnetic transitions with the variation of temperature.^{[94– 96]} Shen et al.^[97] studied the MCE of HTM-TbPdAl compound by magnetization measurements. Figure  39(a) shows the temperature dependence of ZFC and FC magnetizations under a magnetic field of 0.05  T for HTM-TbPdAl compound. It can be seen that the TbPdAl undergoes a PM– AFM transition around T_N = 43  K. In addition, another anomaly is observed at T_t = 22  K, which is associated with an AFM structure transition of frustrated Tb moments from purely commensurate AFM to incommensurate AFM magnetic structure.^{[98, 99]} Moreover, the discrepancy between ZFC and FC curves below 30  K is likely related to the frustration effects of the magnetic structures. Figure  39(b) shows the temperature dependence of Δ S_M for HTM-TbPdAl under different magnetic field changes.^[97] A small positive Δ S_M value can be observed below T_N under relatively low magnetic field changes, which is due to the disordered magnetic sublattices antiparallel to the applied magnetic field. But the Δ S_M gradually changes to negative value with the increase of magnetic field. Such a sign change of Δ S_M indicates the occurrence of field-induced AFM– FM magnetic transition, which leads to a more ordered magnetic configuration. It is found that the Δ S_M– T curve shows a small peak around T_t, which is associated with AFM structure transition of frustrated Tb moments. In addition, a large – Δ S_M value of 11.4  J/kg· K for a field change of 5  T is obtained around T_N, which is due to the field-induced AFM– FM transition. Moreover, the Δ S_M peak expands in a wide temperature range, leading to a high RC value of 350  J/kg for a field change of 5  T.

Fig.  39.

	Figure Option ViewDownloadNew Window
	Fig.  39. (a) Temperature dependence of ZFC and FC magnetizations under a magnetic field of 0.05  T for HTM-TbPdAl compound. (b) Temperature dependence of Δ SM for HTM-TbPdAl under different magnetic field changes.[97]

Recently, Xu et al.^{[100, 101]} systematically investigated the magnetic properties and MCE of RPdAl (R = Gd– Er) compounds with different crystal structures, and found that the magnetic properties and MCE could be affected significantly by the variation of crystal structure. Two series of RPdAl compounds were annealed at 750  ° C for 50 days and at 1050  ° C∼ 1080  ° C for 10∼ 12 days, respectively. Figure  40 shows the XRD patterns and crystal structures of these two series of RPdAl compounds at room temperature.^{[32, 100]} The XRD measurements confirm that the low-temperature annealed samples crystallize in an orthorhombic TiNiSi-type structure as stable LTM (space group Pnma) while the high-temperature annealed compounds crystallize in a hexagonal ZrNiAl-type structure as metastable HTM (space group ). In addition, it is noted that both series of RPdAl crystallize in a purely single phase. The lattice parameters and unit cell volumes determined from the Rietveld refinement are summarized in Table  3.^{[32, 100]} It is found that the LTM-RPdAl compounds exhibit larger unit volume than that of HTM-RPdAl. Moreover, the lattice constants and unit cell volumes decrease linearly with the R atom type sweeping from Gd to Er, which is attributed to the lanthanide contraction.

Fig.  40.

	Figure Option ViewDownloadNew Window
	Fig.  40. XRD patterns and crystal structures of (a) LTM-RPdAl and (b) HTM-RPdAl compounds at room temperature, respectively.[32, 100]

Table 3.

Table 3.

Table 3. The lattice parameters and unit cell volumes of LTM- and HTM-RPdAl compounds determined from the Rietveld refinement.[32, 100] RPdAl a/nm b/nm c/nm V/nm3 R = Gd LTM 0.69668(0) 0.44477(9) 0.77586(1) 0.2404(1) HTM 0.72002(2) 0.40265(1) 0.1807(8) R = Tb LTM 0.69152(7) 0.44274(6) 0.77422(5) 0.2370(4) HTM 0.71816(8) 0.39973(9) 0.1785(5) R = Dy LTM 0.68823(5) 0.44153(4) 0.77332(8) 0.2349(9) HTM 0.71893(4) 0.39593(1) 0.1772(2) R = Ho LTM 0.68527(4) 0.44037(9) 0.77242(8) 0.2331(0) HTM 0.71857(5) 0.39320(9) 0.1758(3) R = Er LTM 0.68142(7) 0.43868(5) 0.77087(9) 0.2304(4) HTM 0.71830(0) 0.39080(4) 0.1746(2)

Table 3. The lattice parameters and unit cell volumes of LTM- and HTM-RPdAl compounds determined from the Rietveld refinement.[32, 100]

Figure  41 displays the temperature dependence of magnetization under a magnetic field of 0.01  T for LTM-RPdAl compounds.^{[32, 100]} It is found that all LTM-RPdAl (R = Gd– Er) compounds order antiferromagnetically with the decrease of temperature, and the T_N is determined to be 31, 45, 21, 10, and 10  K for R = Gd, Tb, Dy, Ho, and Er, respectively. Besides, TbPdAl and ErPdAl exhibit another AFM– AFM magnetic transition around T_t = 24  K and 4  K, respectively. However, the magnetic structures and properties turn out to be much different in HTM-RPdAl compounds. Figure  42 shows the temperature dependence of magnetization for HTM-RPdAl compounds.^{[32, 100]} It can be found that all compounds, except ErPdAl exhibiting a single AFM– PM transition at T_N = 5  K, show two successive magnetic transitions with the variation of temperature.

It is seen from Fig.  42(a) that the HTM-GdPdAl undergoes an FM– PM transition at T_C = 49  K followed by a spin reorientation at T_SR = 16  K. In addition, it is interesting that HTM-GdPdAl experiences an isostructural phase transition around 180  K from a high-temperature HTM  I phase to a low-temperature HTM  II phase, which leads to changes of lattice parameters, electrical resistance, magnetic susceptibility, etc.^[95] With the decrease in temperature, HTM-TbPdAl undergoes a PM– AFM transition around T_N = 43  K followed by an AFM structure transition at T_t = 22  K, which is in a good agreement with the result of Shen et al.^[97] In HTM-TbPdAl with hexagonal ZrNiAl-type structure, one-third of the Tb moments (Tb2) are highly frustrated in the temperature range of T_N and T_t, and this geometrical frustration of Tb2 spins results in an AFM structure transition from a purely commensurate AFM structure at higher temperature to a purely incommensurate AFM magnetic structure when T < T_t. Besides, two-third of the non-frustrated Tb moments (Tb1 and Tb3) exhibit commensurate AFM ordering below T_N. HTM-DyPdAl undergoes two successive magnetic phase transitions with a decrease of temperature: a PM– FM transition at T_C = 22  K followed by a spin reorientation transition at T_SR = 14  K. These transition temperatures are a little lower than the data (T_C = 25  K and T_SR = 17  K) obtained by AC susceptibility and electrical resistance measurements.^{[96, 102]} The isostructural phase transition from HTM  I phase to HTM  II phase is not observed in HTM-DyPdAl compound. The x-ray photoelectron spectroscopy (XPS) studies reveal that the localization of the Pd 4d orbitals and the hybridization processes contribute to the coupling of the system in HTM  II phase, and thus the disappearance of HTM  II phase is likely related to the weak molecular field and absence of such coupling.^{[96, 103]} Talik et al.^[102] found that the single crystal HTM-DyPdAl exhibits distinct magnetic hysteresis and several metamagnetic transitions with the magnetic field applied along a axis, while it exhibits perfect magnetic reversibility along c axis. This fact indicates that HTM-DyPdAl may have a canted magnetic structure with an AFM moment component along the a axis. It can be seen from Fig.  42(d) that HTM-HoPdAl undergoes a PM– AFM transition at T_N = 12  K. Besides, another transition is observed around T_t = 4  K, which corresponds to an AFM– AFM transition. Similar to HTM-DyPdAl, Talik et al.^[104] found that the overlap of 4d orbitals of neighboring Pd atoms in HTM-HoPdAl is also reduced due to the formation of a narrow Pd 4d band. Therefore, the coupling of the system in HTM  II phase is weakened with the reduction of the localization of Pd 4d orbitals and the hybridization processes, and thus isostructural phase transition from HTM  I phase to HTM  II phase cannot occur in HTM-HoPdAl. In addition, the magnetic measurements on single crystal reveal that HTM-HoPdAl exhibits high magnetocrystalline anisotropy. The AFM characteristic can be found in the thermal variation of magnetization along a axis, and it correlates with the increase of lattice parameter a. Along the c axis, HTM-HoPdAl exhibits an FM characteristic accompanied by a shrinkage of lattice parameter c.

Fig.  41.

	Figure Option ViewDownloadNew Window
	Fig.  41. Temperature dependence of magnetization under a magnetic field of 0.01  T for LTM-RPdAl compounds.[32, 100]

Fig.  42.

	Figure Option ViewDownloadNew Window
	Fig.  42. Temperature dependence of magnetization under low magnetic field for HTM-RPdAl compounds.[32, 100]

Figure  43 shows the magnetization isotherms and the temperature dependence of Δ S_M under different magnetic field changes for HTM-RPdAl (R = Gd, Tb, and Dy) compounds.^{[32, 100]} The magnetization of HTM-GdPdAl below T_C increases rapidly at low fields and tends to saturate with increasing field, corresponding to typical FM behavior. In addition to the Δ S_M peak at T_C, another Δ S_M peak can be observed around T_SR = 16  K. These two successive peaks result in a table-like Δ S_M– T curve between T_C and T_SR, which is favorable to the Ericsson-cycle magnetic refrigeration. For the field changes of 2  T and 5  T, the maximum – Δ S_M values of HTM-GdPdAl are 5.3  J/kg· K and 9.2  J/kg· K, respectively. A field-induced metamagnetic transition from AFM to FM states is observed below T_N in HTM-TbPdAl as seen in Ref.  [97], and the negative slope of Arrott plots below T_N confirms that the nature of this metamagnetic transition is of first-order. The critical field for metamagnetic transition is obtained to be 0.55  T at 9  K, and this relatively low critical field suggests the possible large MCE in HTM-TbPdAl compound. The maximum – Δ S_M values for the magnetic field changes of 2  T and 5  T are 5.8  J/kg· K and 11.4  J/kg· K, respectively, which are consistent with the results of Shen et al.^[97] Compared with GdPdAl and HoPdAl, the HTM-DyPdAl is much harder to magnetize to saturation even with the application of 14  T. Since the PM– FM and SR transitions take place closely, the two Δ S_M peaks overlap with each other and then lead to a single Δ S_M peak. A similar phenomenon has also been observed in other systems, such as ErGa^[105] and Ho₃Al₂.^[106] For the field changes of 2, 5, and 7  T, the maximum – Δ S_M values of HTM-DyPdAl are 7.8, 14.7, and 17.8  J/kg· K, respectively. The Δ S_M peak broadens asymmetrically towards high temperature with increasing field, suggesting the possible presence of short-range FM correlations in the PM region.

Fig.  43.

	Figure Option ViewDownloadNew Window
	Fig.  43. Magnetization isotherms and the temperature dependence of Δ SM under different magnetic field changes for HTM-RPdAl (R = Gd, Tb, and Dy) compounds.[32, 100]

The magnetization isotherms of LTM-RPdAl and HTM-RPdAl (R = Ho and Er) under applied fields up to 7  T are displayed in Fig.  44.^{[100, 101]} For LTM-RPdAl (R = Ho and Er) compounds, a field-induced metamagnetic transition from AFM to FM states can be clearly seen below T_N with the increase of magnetic field. On the contrary, HTM-RPdAl (R = Ho and Er) compounds exhibit a weak metamagnetic transition at lower fields and then tend to saturation with a higher magnetization in comparison with that of LTM-RPdAl. For example, the H_cr and M_{7  T} at 2  K are 1.5  T and 141  A/m²· kg for LTM-HoPdAl, and 0.15  T and 163  A/m²· kg for HTM-HoPdAl, respectively.^[101] This fact indicates that the AFM coupling in LTM-RPdAl is much stronger than that in HTM-RPdAl compounds. Figure  45 shows the Arrott plots of LTM-RPdAl and HTM-RPdAl (R = Ho and Er) compounds.^{[100, 101]} According to the Banerjee criterion, ^[107] a magnetic transition is considered as first-order when the Arrott plots exhibit negative slope or inflection point; otherwise it is expected to be of second-order when the Arrott plots exhibit positive slope. It is clearly seen that the slope of Arrott plots below T_N is negative for all compounds, further confirming the first-order AFM– FM metamagnetic transition. On the other hand, the positive slope of all Arrott plots above T_N proves the nature of a field-induced second-order PM– FM transition. The temperature dependence of Δ S_M for LTM-RPdAl and HTM-RPdAl (R = Ho and Er) compounds under different magnetic field changes are shown in Fig.  46.^{[100, 101]} A small positive value of Δ S_M is observed at low temperatures and low fields, but it gradually changes to negative value with the increase of magnetic field. Such a sign change of Δ S_M is due to the field-induced metamagnetic transition from AFM to FM states. For the field changes of 2, 5, and 7  T, the maximum – Δ S_M values are 12.8, 20.6, and 23.6  J/kg· K for of HTM-HoPdAl, and 12.0, 24.3, and 28.4  J/kg· K for HTM-ErPdAl, respectively. These Δ S_M values are comparable with or even larger than those of some magnetocaloric materials in the same temperature range.^{[67, 79, 108– 110]} However, the maximum – Δ S_M values for a field change of 5  T are 13.7 and 11.6  J/kg· K for LTM-HoPdAl and LTM-ErPdAl compounds, respectively. This lower MCE is attributed to the strong AFM coupling in LTM-RPdAl compounds. Consequently, the MCE of LTM-RPdAl and HTM-RPdAl are summarized in Table  2. The relatively high Δ S_M and RC values for HTM-RPdAl suggest them as promising materials for magnetic refrigeration in low temperature range.

Fig.  44.

	Figure Option ViewDownloadNew Window
	Fig.  44. Magnetization isotherms of LTM-RPdAl and HTM-RPdAl (R = Ho and Er) under applied fields up to 7  T.[100, 101]

Fig.  45.

	Figure Option ViewDownloadNew Window
	Fig.  45. Arrott plots of LTM-RPdAl and HTM-RPdAl (R = Ho and Er) compounds.[100, 101]

Fig.  46.

	Figure Option ViewDownloadNew Window
	Fig.  46. Temperature dependence of Δ SM for LTM-RPdAl and HTM-RPdAl (R = Ho and Er) compounds under different magnetic field changes.[100, 101]