Cite this Article
Chen Li-Min, Guo Ying, Liu Xu-Guang, Xie Qi-Yun, Tao Zhi-Kuo, Chen Jing, Zhou Ling-Ling, Liu Chun-Sheng†. Fabrication and magnetic properties of 4SC(NH2)2–Ni0.97Cu0.03Cl2 single crystals . Chinese Physics B, 24(12): 127503  
Permissions
Fabrication and magnetic properties of 4SC(NH2)2–Ni0.97Cu0.03Cl2 single crystals
Chen Li-Mina), Guo Yingb), Liu Xu-Guangc), Xie Qi-Yuna), Tao Zhi-Kuoa), Chen Jinga), Zhou Ling-Linga), Liu Chun-Sheng†a)
Key Laboratory of Radio Frequency and Micro-Nano Electronics of Jiangsu Province, Nanjing 210023, China
Jiangsu Key Laboratory of Big Data Analysis Technology; Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology, Nanjing 210044, China
Hefei National Laboratory for Physical Sciences at Microscale, University of Science and Technology of China, Hefei 230026, China

†Corresponding author. E-mail: csliu@njupt.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11404316 and 11304159), the Natural Science Foundation of Jiangsu Province, China, and the Science Foundation of Nanjing University of Posts and Telecommunications, China (Grant Nos. BK20140863 and NY213075).

Abstract

Single crystals of 4SC(NH2)2–Ni1− xCu xCl2 ( x = 0.03) (Cu-DTN) containing spin S = 1/2 Cu2 + and S = 1 Ni2+ cations are synthesized by slow evaporation methods. Structural characterization demonstrates that the Cu-DTN is of a tetrahedral structure with lattice parameter c being 9.0995 Å, which is 1.32% expansion compared with that of parent material DTN due to the larger radius of the Cu ion. Direct current (DC) susceptibility measurements show that both the antiferromagnetic exchange interaction at low temperature and the large anisotropy of susceptibilities are suppressed after doping the Cu ion, which could be related to the structural distortion and the increase of the super-exchange paths in Cu-DTN.

PACS: 75.30.Hx; 75.30.Cr; 75.30.Gw
Keyword: magnetic metal-doped; magnetic materials; susceptibility; antiferromagnetic interaction
1.Introduction

Low-dimensional frustrated spin systems have attracted extensive attention due to their rich magnetic ground states arising from a complex interplay of thermal and quantum fluctuations. Previous studies have demonstrated that in a one-dimensional (1D) antiferromagnetic (AFM) chain system with spin S = 1/2, a gapless ground state would be formed.[1] However, for a 1D AFM chain system with spin S = 1, a finite energy gap between the lowest lying singlet ground state and the first excited triplet state might emerge.[2] So far, a lot of research on the low-dimensional AFM chain systems focused on the magnetic ions with mixed-spin states, [2– 9] such as quasi-1D mixed-spin antiferromagnetic materials R2BaNiO5 (R = Pr, Nd or NdxY1− x) with the S = 1 Ni2+ and the R3+ magnetic ions, in which the coexistence of long-range order and Haldane gap excitations was observed, [10, 11] and spin-peierls system Cu1− xCdxGeO3 with a finite gap appears at the spin-peierls phase transition.[12– 16]

4SC(NH2)2– NiCl2 (DTN) with antiferromagnetic S = 1 chains of Ni2+ ions, is the best-known candidate for the Bose– Einstein condensation studies in magnetic fields.[17] By doping low concentration of nonmagnetic halogen Br ions in the model compound DTN, a Bose glass of field-induced magnetic quasiparticles was observed due to the induced disorder by the doped Br atoms.[18] On the other hand, in a pure spin S = 1/2 chain system of Cu2+ ions, spontaneous three-dimensional long range antiferromagnetic order will emerge, such as (CH3)2NH2CuCl3 (MCCL).[19, 20] If the S = 1 Ni2+ ions in DTN can be replaced by other atoms with spin of half integer, such as Cu2+ ions, novel physical properties can be highly expected.

In this paper, we report the synthesis of the spin S = 1/2 Cu2+ -doped DTN single crystals 4SC(NH2)2– Ni1− xCuxCl2 (x = 0.03) (Cu-DTN). The Cu-DTN with single crystalline quality exhibits a tetrahedral structure with c being 9.0995  Å , which is slightly larger than that of the parent material DTN due to the larger radius of Cu2+ . Magnetic measurements show that after Cu ions are doped, the broad maximum magnetic susceptibility peak shifts to low temperature, indicating the weakening of the AFM short-range order interaction, and almost isotropic magnetic properties are observed. The significant change of the magnetic behavior of the Cu-DTN is related to the structural distortion and the emergence of novel super-change paths caused by Cu2+ ion doping.

2.Experiment

The single crystal Cu-DTN was synthesized by the slow evaporation method in a water bath environment at a constant temperature.[21] The grown crystals were identified by x-ray powder diffraction (XRD) using Cu Kα radiation with a scanning rate of 0.02° /min. The chemical compositions were determined by energy dispersive x-ray spectrometry (EDX). The DC magnetic susceptibility values were measured by using a SQUID-VSM magnetometer (Quantum Design) with the magnetic field up to 7  T applied perpendicularly and parallelly to the c axis of the sample, respectively.

3.Results and discussion
3.1.Structural analysis

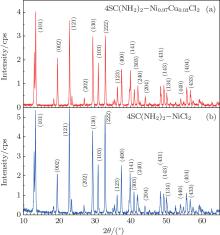
Figure  1(a) shows the x-ray diffraction patterns of the prepared Cu-DTN. All the diffraction patterns can be indexed to the 4SC(NH2)2– Ni1− xCuxCl2 with x = 0.03. No other diffraction peaks were observed, indicating the high purity of the synthesized Cu-DTN. For comparison, the diffraction patterns of DTN are also collected as shown in Fig.  1(b). It can be seen that after the Cu2+ ions are doped, the tetragonal structure with space group I4 is still maintained. The lattice parameters derived from the single-crystal XRD diffraction pattern are a = 9.6018  Å , b = 9.6018  Å , and c = 9.0995  Å . Comparing with the parameters of pure DTN, [22, 23] after Cu2+ ions are doped, the c lattice parameter and a (b) axis are enlarged about 1.62% and 0.45%, respectively. The large expansion of the c lattice parameter is related to the radius of Cu2+ ion larger than that of Ni2+ ion in DTN, which can lead to structural distortion. Meanwhile, Cu2+ ions-doped DTN could also induce new types of super-exchange paths, i.e., Cu– Cl– Cl– Ni, Ni– Cl– Cl– Cu, and Cu– Cl– Cl– Cu, which is a prerequisite for novel magnetic properties for Cu-DTN.

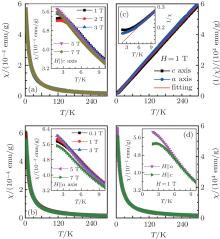
Fig.  1. The x-ray powder diffraction patterns of 4[SC(NH2)2]– Ni0.97Cu0.03Cl2 crystals (a) and 4[SC(NH2)2]– NiCl2 crystals (b) at room temperature.

3.2.Magnetic properties

Figure  2 shows the magnetic susceptibilities of the Cu-DTN single crystals in a temperature range from 2  K to 300  K with magnetic fields H perpendicular (χ a) and parallel (χ c) to the c axis, respectively. As seen in Fig.  2(a), when the magnetic field is applied along the c axis, the magnetic susceptibilities almost increase monotonically as temperature decreases. The inset shows that a broad maximum peak can be observed in a low magnetic field regime, similar to that of the magnetic susceptibility of pure DTN, which is associated with the occurrence of a short-range AFM ordering. The maximum peak that appears is determined to be Tmax ∼ 3  K under H = 1  T, which is a little smaller than that of the pure DTN (∼ 6  K).[22] With magnetic field increasing, the peak shifts to a lower temperature, and no peak can be observed in the whole temperature regime when the applied magnetic field increases to higher than 5  T. The disappearance of the peak indicates that the AFM short-range order interaction is strongly suppressed under a high applied magnetic field. However, the magnetic susceptibility shows a magnetic field-independent behavior at a high temperature, and the curves almost overlapped with magnetic field changing from 0 to 7  T.

Fig.  2. Temperature-dependent magnetic susceptibilities for (a) H ‖ c and (b) H ‖ a. (c) Curie– Weiss law (red line) fitting the reciprocal susceptibility 1/χ c (black line), the inset shows the low temperature regime (blue line denotes 1/χ a). (d) Magnetic susceptibility as a function of temperature under H = 1  T, with magnetic field applied along c axis and a axis, respectively. Inset shows the scenarios of the low temperature regime.

The magnetic properties of Cu-DTN, with the magnetic field applied along the a axis, are also investigated as shown in Fig.  2(b). The magnetic susceptibilities also increase monotonically as temperature decreases, which is similar to that when a magnetic field is applied parallelly to the c axis. It is noted that no obvious broad maximum peak can be observed even when the temperature decreases to 2  K. However, clear deviations between the reciprocal susceptibility and the fitted Curie– Weiss curve are shown in the inset of Fig.  2(c) for magnetic fields applied along the a axis and c axis, respectively, indicating the occurrence of the AFM correlation at low temperature. Curie– Weiss temperature is estimated to be − 4.8  K from the 1/χ − T curves, and the negative Curie temperature further suggests the intrachain interactions in Cu-DTN are AFM correlation.

Contrary to the case of pure DTN, [2, 22] the susceptibilities χ a and χ c of Cu-DTN are almost overlapped in the high temperature regime, indicating nearly isotropic magnetic properties of Cu-DTN as shown in Fig.  2(d). The strong suppression of the anisotropy in Cu-DTN is due to the replacement of the anisotropic Ni ions by isotropic Cu ions. The slight deviation between χ c and χ a at low temperature is related only to spin susceptibility whose anisotropy comes from the different magnetic interactions.

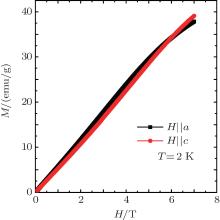
The magnetic field-dependent magnetizations of the Cu-DTN measured at 2  K are shown in Fig.  3. The magnetization exhibits similar behaviors to those when the magnetic field is applied parallelly to the c axis and a axis, respectively. An approximate linear increase with increasing magnetic field can be observed when the magnetic field is lower than 2  T, indicating the AFM exchange interaction in the Cu-DTN. When the magnetic field further increases, a characteristic change in the slope of the curve of magnetization versus magnetic field further demonstrates the suppression of the AFM exchange interaction at high magnetic field, which is consistent with the χ − T measurement in Figs.  2(a) and 2(b).

Fig.  3. Magnetic field dependences of the magnetization at 2  K for magnetic field parallel to different axes.

4.Discussion

Compared with the case of pure DTN, several intriguing magnetic properties emerge after partially replacing a Ni ion with a Cu ion, i.e. the suppression of the antiferromagnetic correlation at low temperature and the suppression of the anisotropy of the DTN.

In the pure DTN, the magnetic coupling occurs mainly through the Ni– Cl– Cl– Ni super-exchange path along the magnetic chain (c axis).[8, 9] However, after doping Cu ions, the larger radius of the Cu ion than that of the Ni ion can result in the distortion of the lattice and weakening of the magnetic interaction coupling Jc. Three new super-exchange paths, i.e., Cu– Cl– Cl– Cu, Cu– Cl– Cl– Ni, and Ni– Cl– Cl– Cu with a weak bonding energy form. According to Goodenough– Kanamori rule, the exchange interaction between the magnetic ions is sensitive to the distances of R– Cl (R = Cu, Ni) and Cl· · · Cl.[24– 30] Therefore, by replacing the Ni ions with Cu ions of large radius, the intra-chain magnetic super-exchange interaction Jc along the c axis can decrease significantly, which results in the suppression of the AFM exchange interaction in Cu-DTN at low temperature as seen in the shift of the broad maximum magnetic susceptibilities peak to a low temperature in Fig.  2(a).

The disappearance of the large anisotropic susceptibility in Cu-DTN can be understood by taking the isotropic properties of the Cu2+ ions into account. The tetragonal symmetry of the DTN crystal is the premise of magnetic phase transitions BEC, in which Ni spins with the large single ion anisotropy D are strongly coupled along the tetragonal axis (c axis). The single-ion anisotropy D generates an on-site repulsion, and the magnetic field acts as a chemical potential. However, after Ni2+ spins are partially substituted by those of Cu2+ in Cu-DTN, the single-ion uniaxial anisotropy is suppressed, and the axial symmetry is also broken in the distorted structure caused by the Cu2+ doping.[31– 33]

Considering the difference in spin state between Cu2+ and Ni2+ , the ground state of Cu-DTN also changes. After doping Cu2+ , four probable super-change paths, i.e., Ni– Cl– Cl– Ni, Cu– Cl– Cl– Cu, Cu– Cl– Cl– Ni, and Ni– Cl– Cl– Cu, will be formed, disordered, and distributed due to the random replacement of Ni2+ by Cu2+ . It is noted that the two new kinds of super-change paths, i.e., Cu– Cl– Cl– Ni and Ni– Cl– Cl– Cu, are composed of magnetic ions with S = 1/2 (Cu2+ ) and S = 1 (Ni2+ ), respectively, and the interaction along these two paths is different from that between Cu– Cl– Cl– Cu with gapless ground state and Ni– Cl– Cl– Ni with finite gap ground state. For instance, due to the correlations between inter- and intra-chains interactions and the frustration effects of spins and lattice significantly changed after doping Cu2+ ions, the long-range AFM order is expected. However, due to the limitation of the experiment setup, the magnetic properties neither in ultralow temperature regime nor in higher field can be detected now, which are still worth further exploring.

5.Conclusions

The crystal structure and magnetic properties of Cu doping DTN are studied. Compared with the pure DTN, Cu-DTN has the same crystal structure while the lattice parameters slightly expand due to the larger radius of Cu2+ ions. The reciprocal susceptibilities 1/χ c and /χ a exhibit a Curie– Weiss behavior at high temperature with a Curie– Weiss temperature of − 4.8  K and the AFM short-range order correlation at low temperature. The susceptibility with the downward shift of the maximum peak shows the weak anisotropy, indicating the weaker intra-chain magnetic interactions induced by doping Cu2+ and the suppressed large single-ion anisotropy of Ni2+ ions.

Reference
1 Johnston D C, Kremer R K, Troyer M, Wang X, Klümper A, Bud’ko S L, Panchula A F and Canfield P C 2000 Phys. Rev. B 61 9558 DOI:10.1103/PhysRevB.61.9558 [Cited within:1]
2 Zvyagin S, Wosnitza J, Batista C D, Tsukamoto M, Kawashima N, Krzystek J, Zapf V S, Jaime M, Oliveira N F and Paduan-Filho AJr 2007 Phys. Rev. Lett. 98 047205 DOI:10.1103/PhysRevLett.98.047205 [Cited within:3]
3 Nikuni T, Oshikawa M, Oosawa A and Tanaka H 2000 Phys. Rev. Lett. 84 5868 DOI:10.1103/PhysRevLett.84.5868 [Cited within:1]
4 Yamada F, Ono T, Fujisawa M, Tanaka H and Sakakibara T 2007 J. Magn. Magn. Mater. 310 1352 DOI:10.1016/j.jmmm.2006.10.372 [Cited within:1]
5 Jaime M, Correa V F, Harrison N, Batista C D, Kawashima N, Kazuma Y, Jorge G A, Stern R, Heinmaa I, Zvyagin S A, Sasago Y and Uchinokura K 2004 Phys. Rev. Lett. 93 087203 DOI:10.1103/PhysRevLett.93.087203 [Cited within:1]
6 Sebastian S E 2005 Phys. Rev. B 72 100404 DOI:10.1103/PhysRevB.72.100404 [Cited within:1]
7 Radu T, Wilhelm H, Yushankhai V, Kovrizhin D, Coldea R, Tylczynski Z, Lühmann T and Steglich F 2005 Phys. Rev. Lett. 95 127202 DOI:10.1103/PhysRevLett.95.127202 [Cited within:1]
8 Sun X F, Tao W, Fan C and Wang X M 2009 Phys. Rev. Lett. 102 167202 DOI:10.1103/PhysRevLett.102.167202 [Cited within:1]
9 Zapf V S, Zocco D, Hansen B R, Jaime M, Harrison N, Batista C D, Kenzelmann M, Niedermayer C, Lacerda A and Paduan-Filho A 2006 Phys. Rev. Lett. 96 077204 DOI:10.1103/PhysRevLett.96.077204 [Cited within:2]
10 Buttrey D J, Sullivan J D and Rheingold A L 1990 J. Solid State Chem. 88 291 DOI:10.1016/0022-4596(90)90226-N [Cited within:1]
11 Maslov S and Zheludev A 1998 Phys. Rev. B 57 68 [Cited within:1]
12 Hase M, Terasaki I, Sasago Y, Uchinokura K and Obara H 1993 Phys. Rev. Lett. 71 4059 DOI:10.1103/PhysRevLett.71.4059 [Cited within:1]
13 Oseroff S B, Cheong S W, Aktas B, Hundley M F, Fisk Z and Rupp L W 1995 Phys. Rev. Lett. 74 1450 DOI:10.1103/PhysRevLett.74.1450 [Cited within:1]
14 Lussier J G, Coad S M, McMorrow D F and Paul D M K 1995 J. Phys. : Condens. Matter 7 L325 DOI:10.1088/0953-8984/7/25/003 [Cited within:1]
15 Sasgo Y, Koide N, Uchinokura K, Martin M C, Hase M, Hirota K and Shirane G 1996 Phys. Rev. B 54 R6835 DOI:10.1103/PhysRevB.54.R6835 [Cited within:1]
16 Haravifard S, Rule K C, Dabkowska H A, Gaulin B D, Yamani Z and Buyers W J L 2007 J. Phys. : Condens. Matter 19 436222 DOI:10.1088/0953-8984/19/43/436222 [Cited within:1]
17 Sebastian S E, Zapf V S, Harrison N, Batista C D, Sharma P A, Jaime M, Fisher I R and Lacerda A 2006 Phys. Rev. Lett. 96 189703 DOI:10.1103/PhysRevLett.96.189703 [Cited within:1]
18 Yu R, Yin L, Sullivan N S, Xia J S and Huan C 2012 Nature 489 379 DOI:10.1038/nature11406 [Cited within:1]
19 Yoshida Y, Kitano Y, Inagaki Y, Sakurai T, Kimata M, Okubo S, Ohta H, Koyama K, Motokawa M, Asano T and Ajiro Y 2007 J. Phys. Soc. Jpn. 76 113704 DOI:10.1143/JPSJ.76.113704 [Cited within:1]
20 Inagaki Y, Wada O, Ienaga K, Morodomi H, Kawae T, Yoshida Y, Asano T, Frukawa Y and Ajiro Y 2009J. Phys. : Conf. Ser. 150 042067 DOI:10.1088/1742-6596/150/4/042067 [Cited within:1]
21 Chen L M, Tao W, Zhao Z Y, Li Q J, Ke W P, Wang X M, Liu X G, Fan C and Sun X F 2010 J. Cryst. Growth 312 3243 DOI:10.1016/j.jcrysgro.2010.07.055 [Cited within:1]
22 Paduan-Filho A, Chirico R D, Joung K O and Carlin R L 1981 J. Chem. Phys. 74 4103 DOI:10.1063/1.441589 [Cited within:3]
23 Amparo L C and Truter M R 1963 J. Chem. Soc. 245 1309 [Cited within:1]
24 Turnbull M M, Land ee C P and Wells B M 2005 Coord. Chem. Rev. 249 2567 DOI:10.1016/j.ccr.2005.01.015 [Cited within:1]
25 Block R and Jansen L 1982 Phys. Rev. B 26 148 [Cited within:1]
26 Willett R D, Butcher R, Land ee C P and Twamley B 2005 Polyhedron 24 2222 DOI:10.1016/j.poly.2005.03.121 [Cited within:1]
27 Snively L O, Haines D N, Emerson K and Drumheller J E 1982 Phys. Rev. B 26 5245 DOI:10.1103/PhysRevB.26.5245 [Cited within:1]
28 Willett R D, Twamley B, Montfrooij W, Granroth G G, Nagler S E, Hall D W, Park J H, Watson B C, Meisel M W and Talham D R 2006 Inorg. Chem. 45 7689 DOI:10.1021/ic060654u [Cited within:1]
29 Straatman P, Block R and Jansen L 1984 Phys. Rev. B 29 1415 DOI:10.1103/PhysRevB.29.1415 [Cited within:1]
30 Marsh W E, Hatfield W E and Hodgson D J 1988 Inorg. Chem. 27 1819 DOI:10.1021/ic00283a028 [Cited within:1]
31 Paduan-Filho A, Gratens X and Oliveira N F 2004 Phys. Rev. B 69 020405 DOI:10.1103/PhysRevB.69.020405 [Cited within:1]
32 Zapf V S, Correa V F, Batista C D, Murphy T P, Palm E D, Jaime M, Tozer S, Lacerda A and Paduan-Filho A 2007 J. Appl. Phys. 101 DOI:10.1063/1.271161209E106 [Cited within:1]
33 Zvyagin S A, Wosnitza J, Kolezhuk A K, Zapf V S, Jaime M, Paduan-Filho A, Glazkov V N, Sosin S S and Smirnov A I 2008 Phys. Rev. B 77 092413 DOI:10.1103/PhysRevB.77.092413 [Cited within:1]