With the growing demand for the high-performance lithium ion batteries (LIBs), LiMn₂O₄ with spinel structure has attracted much attention owing to the low cost of manganese and one-dimensional Li-ion migration pathway.^{[1– 4]} LiMn₂O₄ crystallizes in the space group Fd-3m, and Li, Mn, and O occupy 8a, 16d, and 32e sites, respectively. Owing to the redox Mn³⁺ /Mn⁴⁺ , LiMn₂O₄ shows a reversible capacity of nearly 135  mA· h· g^{− 1}.^[4] However, the unsatisfactory cycle stability and voltage degradation prevent it from being further used as the potential cathode material for LIBs. Many efforts have been made to improve its electrochemical performance via partially substituting Mn by Co, Ni, Cr or Fe.^{[5– 8]}

A study on the crystallographic, electronic and magnetic structure of the cathode material is meaningful for the understanding of the electrochemical property since cation ordering and phase stability are closely related to the charge capacity and capacity retention. LiMn₂O₄ has been found to show a magnetic transition from paramagnetism to spin glass (SG) because of the geometrical frustration.^[9] When Mn ions are partly substituted by Cr, an SG is also found in LiCrMnO₄ due to the random distribution of Cr³⁺ and Mn⁴⁺ ions.^[10] LiCoMnO₄ is another attractive cathode material because it can provide a high voltage plateau above 5  V.^[5] Electron paramagnetic resonance (EPR) spectrum of LiCoMnO₄ suggests a low-spin state of Co³⁺ state with S = 0.^[11] Interestingly, if Co³⁺ ions occupy 16d site homogeneously, the nonmagnetic ions will act as the dilution to the magnetic interaction and paramagnetism is expected. In this paper, an SG transition is proposed in LiCoMnO₄ by the comprehensive magnetic method. In contrast to the expected paramagnetism, the existence of SG transition can be explained on the basis of cation random distribution in LiCoMnO₄.

LiCoMnO₄ was prepared by a solid-state reaction. Stoichiometric mixtures of Li₂CO₃, Co₂O₃, and Mn₂O₃ were ground thoroughly, and fired at 650  ° C or 6  h and then at 850  ° C or 24  h before cooling to room temperature naturally. The crystal structure of the as-prepared sample was studied by x-ray diffraction (XRD) in capillary transmission mode on a STOE STADI P diffractometer with Mo Kα ₁ radiation. Diffraction data were recorded over a 2θ range of 5° – 80° in steps of 0.01° . The software Fullprof was used for data analysis and Rietveld refinement of the structural model. Magnetic characterization was performed by a superconducting quantum interference device magnetometer (Quantum Design MPMS-XL).

Figure  1 shows the XRD pattern for the as-prepared LiCoMnO₄. Rietveld refinement confirms the spinel structure with space group of Fd-3m and no impurity phase can be detected. Detailed refinement parameters are listed in Table  1. Note that the relative intensities of (311) and (400) peaks are different from those of LiMn₂O₄, ^[12] which may come from the Td and 16c defects due to the random distributions of Mn⁴⁺ and Co³⁺ ions at the 8a and 16c sites, respectively. The degrees of Td and 16c defects are calculated to be 14.9% and 0.9%, respectively, by means of the Rietveld refinement.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Observed and calculated x-ray diffraction profiles together with their difference for the as-prepared LiCoMnO4 compound; (b) Schematic diagram for the crystal structure of spinel LiMn2O4.

Table 1.

Table 1.

Table 1. LiCoMnO4 crystal structure parameters determined by Rietveld refinement. Atom Wyckoff position x y z Occupancy Li 8a 0.12500 0.12500 0.12500 0.85056 Mn 8a 0.12500 0.12500 0.12500 0.07472 Co 8a 0.12500 0.12500 0.12500 0.07472 Li2 16d 0.50000 0.50000 0.50000 0.07472 Mn2 16d 0.50000 0.50000 0.50000 0.45802 Co2 16d 0.50000 0.50000 0.50000 0.45802 Mn3 16c 0.00000 0.00000 0.00000 0.00462 Co3 16c 0.00000 0.00000 0.00000 0.00462 O 32e 0.26204 0.26204 0.26204 1.00000 Space group: Fd-3m Lattice constant: a = 8.07309,   Rwp = 12.2, Rexp = 9.93,   Rf = 4.06.

Table 1. LiCoMnO4 crystal structure parameters determined by Rietveld refinement.

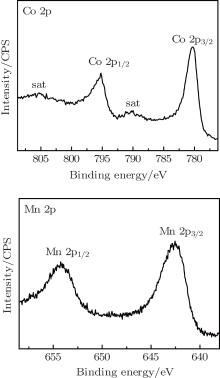
XPS spectra were carried out to further study the valence states of Co and Mn ions as shown in Fig.  2. In the Co 2p spectrum, the binding energies of the peaks located at 780.2  eV and 795.2  eV correspond to 2p_3/2 and 2p_1/2 of Co³⁺ , in accordance with those reported in LiCoO₂, along with two satellite peaks at 790.1  eV and 805.3  eV.^[13] In the Mn 2p spectrum, the peak located at 642.5  eV agrees with the 2p_3/2 of Mn⁴⁺ as reported in Ref.  [14].

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Co 2p and Mn 2p XPS of LiCoMnO4.

Zero-field cooled (ZFC) and field-cooled (FC) susceptibilities from 5  K to 300  K under an applied field of 1000  Oe (1  Oe= 79.5775  A· m^{− 1}) are exhibited in Fig.  3 with the inverse susceptibility curve as indicated in the inset. At high-T, the susceptibility increases with the decrease of temperature, indicating a paramagnetic behavior. By fitting the Curie-Weiss law using high-temperature paramagnetic data, Curie and Weiss constants are calculated to be C = 1.84  emu· K/mol· Oe and θ = − 49(1)  K, respectively. The negative Weiss constant indicates the antiferromagnetic interaction between spins in LiCoMnO₄. 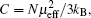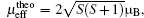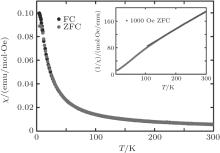By employing the equation where N is the molar concentration of ions and μ _B is the Bohr magneton, the experimental effective moment is calculated to be 3.83(2)  μ _B. On the other hand, the theoretical effective moment should come from the contribution of Mn⁴⁺ ions (S = 3/2), since Co³⁺ ions are suggested to be in the low-spin state in the octahedral coordination by ESR measurements with six 3d electrons in three t_2g orbits, S = 0.^[15] Hence the theoretical effective moment of LiCoMnO₄ is calculated to be 3.87  μ _B via where S equals the spin quantum of Mn⁴⁺ (S = 3/2). The obtained value is consistent with the experimental effective moment of LiCoMnO₄.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. ZFC/FC curves of LiCoMnO4 under 1000  Oe and reciprocal ZFC curve with the Curie– Weiss fitting in inset.

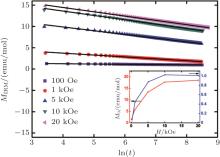
At low-T, ZFC and FC curves begin to show an irreversible behavior at nearly 17  K, and ZFC branch displays a peak at 7  K, which is defined as the freezing temperature (T_f), reminiscence of an SG transition. To confirm the SG transition, the isothermal remanent magnetizations (M_IRM) are recorded and shown in Fig.  4. Applying a procedure in which the sample is zero-field cooled to 5  K and different magnetic fields are applied for 10  min, a slow decay of the M_IRM after the field is reduced to zero, which is a typical feature for the spin glass behavior below T_f.^[16] By fitting the time dependence of magnetization using the formula M_IRM(t) = M₀ − α ln(t), we can obtain the fitting parameters M₀ and α as a function of magnetic field (the inset of Fig.  4). Both the parameters first increase and then tend to saturate at high magnetic fields, which is a typical feature for SG system.^[17]

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Plots of isothermal remanent magnetization versus natural logarithm of time at different applied magnetic fields, and plots of fitting parameters M0 and α in fitting formula MIRM(t) = M0 − α ln(t) versus magnetic field (in inset).

The dynamic behavior of SG near T_f is also studied, and AC susceptibilities under different frequencies ranging from 1  Hz to 500  Hz are shown in Fig.  5. The height of the peak decreases and the peak position shifts toward the high temperature with the increase of frequency, in accordance with the characteristics of SG behavior. Supposing the existence of an equilibrium phase transition with a divergence of relaxation time (τ ) near the transition temperature, we employ the power law to explain the relaxation behavior in the SG system. The power law can be described as τ = τ ₀(T_f/T_g − 1)^{− zv}, where T_g corresponds to the relaxation temperature, τ ₀ is related to the relaxation time of the individual magnetic moment, and zv is the dynamic critical exponent.^[18] The values are calculated to be τ ₀ = 6.2 × 10^{− 11}  s and zv = 6.9, which fall in the typical values (zv ∼ 7.9 ± 1  K) determined by the simulations of Ogielski for a three-dimensional SG with short-range magnetic interactions.^[19] This also confirms the SG transitions in spinel LiCoMnO₄.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Temperature dependences of the real-part of AC susceptibility in the frequency range from 1  Hz to 500  Hz, and the fitting to power law (in inset).

The field dependences of magnetizations (Fig.  6(a)) under different temperatures are recorded, with the magnified curves indicated in the inset. The magnetization shows a linear dependence on magnetic field at 50  K. The small magnetic hysteresis appears as temperature decreases below T_irr. The coercive field and remanence at 5  K are − 201  Oe and 3.4 × 10^{− 3}  μ _B/Mn, respectively. Note that there is no magnetic saturation at 5  K even under a strong field (5  T), which is consistent with the competition nature between antiferromagnetic and ferromagnetic interaction for SG. The Arrott plot (Fig.  6(b)), obtained from magnetization isotherms, shows strong curvature toward the H/M axis without any intercept on the M² axis, indicating no sign of the spontaneous magnetization.^[20]

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. (a) Variations of magnetic field and magnification of specified parts (in inset) with magnetization and (b) Arrott plots (H/M versus M2), at different fixed temperatures of LiCoMnO4.

Note that the geometrical frustration and disorder are two major reasons for the formation of SG. In the spinel LiMn₂O₄, the tetrahedral arrangement of Mn ions with the same bond distance would give a strong frustration effect and frustration parameter (f) equals 11. Correspondingly, an SG transition is observed in LiMn₂O₄ with T_f = 25  K.^[9] When Mn ions are partly substituted by Cr, an SG is also suggested, but f_Cr is lower than 10, ^[10] which is considered as the critical value at which the geometrical frustration plays an effect. This means that the frustrated tetrahedral arrangement of Mn ions would be destroyed when Cr³⁺ ions are introduced into the lattice. The random distributions of Cr³⁺ and Mn⁴⁺ ions are likely to be responsible for the formation of SG. Usually, nonmagnetic ions act as the dilution to the magnetic interaction, and the doped compounds show paramagnetism. In LiCoMnO₄, if the random distributions of Co³⁺ and Mn⁴⁺ ions are homogeneous, nonmagnetic Co³⁺ ions would destroy the exchange interaction between Mn⁴⁺ ions and paramagnetism is expected in the whole measured T region. But, interestingly, LiCoMnO₄ shows an SG transition like LiCrMnO₄, instead of the expected paramagnetism, and the frustration parameter equals 7, which also implies that nonmagnetic Co³⁺ ions destroy the frustrated lattice. The random distributions of Co³⁺ and Mn⁴⁺ ions are likely to result in the formation of different ions clusters due to the different electronic structures between Mn⁴⁺ ions 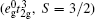and Co³⁺ ions Furthermore, it should be addressed that the differences in preparation method and sintered temperature would induce the difference in the valence state of ions, short-range structural disorder and formation of clusters, especially in the doped materials, which determine the physical and electrochemical properties. For example, the magnetic parameters of layered LiNi_0.4Mn_0.4Co_0.2O₂ show a strong dependence on the preparation method, and the magnetic ground state ranges from SG to cluster-SG.^{[21– 23]} Therefore, how to obtain an ideal LiCoMnO₄ with controlled ion disorder might be a tough question, which needs more studies in future.

We study the structural and magnetic properties of LiCoMnO₄ by Rietveld analysis and DC and AC susceptibilities. The fitting to the high-temperature Curie– Weiss law suggests the low spin state of Co³⁺ ions. The spin glass transition at low temperature is confirmed by the irreversibility between ZFC and FC curve, the isothermal remanent magnetizations, and the fitting to the AC susceptibility peak by using the power law. The origin of SG is attributed to spatial segregation between non-magnetic Co³⁺ clusters and spin glass ordered regions of Mn⁴⁺ clusters rather than geometrical frustration.