Cite this Article
Li Shi-Chang, Zheng Yuan-Lei, Ma Sheng-Gui, Gao Tao†, Ao Bing-Yun‡. First-principles calculation of the electronic structure, chemical bonding, and thermodynamic properties of β-US2 . Chinese Physics B, 24(12): 127101  
Permissions
First-principles calculation of the electronic structure, chemical bonding, and thermodynamic properties of β-US2
Li Shi-Changa), Zheng Yuan-Leia), Ma Sheng-Guia), Gao Tao†a), Ao Bing-Yun‡b)
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
Science and Technology on Surface Physics and Chemistry Laboratory, P. O. Box 9071-35, Jiangyou 621907, China

†Corresponding author. E-mail: gaotao@scu.edu.cn

‡Corresponding author. E-mail: aobingyun@caep.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 21371160 and 21401173).

Abstract

The electronic structure, magnetic states, chemical bonding, and thermodynamic properties of β-US2 are investigated by using first-principles calculation through the density functional theory (DFT) + U approach. The obtained band structure exhibits a direct band gap semiconductor at Γ point with a band gap of 0.9 eV for β-US2, which is in good agreement with the recent experimental data. The charge-density differences, the Bader charge analysis, and the Born effective charges suggest that the U–S bonds of the β-US2 have a mixture of covalent and ionic characters, but the ionic character is stronger than covalent character. The Raman-active, infrared-active, and silent modes at the Γ point are further assigned and discussed. The obtained optical-mode frequencies indicate that the three apparent LO–TO (longitudinal optical–transverse optical) splittings occur in B1u, B2u, and B3u modes, respectively. Furthermore, the Helmholtz free energy Δ F, the specific heat Δ E, vibrational entropy S, and constant volume CV are studied over a range from 0 K∼100 K. We expect that our work can provide some valuable information for further experimental investigation of the dielectric properties and the infrared reflectivity spectrum of uranium chalcogenide.

PACS: 71.27.+a; 31.15.ae; 74.25.Bt
Keyword: β-US2; magnetization; chemical bonding; thermodynamic properties
1. Introduction

The chalcogenide compounds of the actinides, especially of uranium, have attracted extensive attention because of their particular physical properties and their potential applications in nuclear fuels.[1] The β -US2 has attracted much more attention because of its interesting subtle magnetic change.[2, 3] However, the localized and strongly correlated 5f electrons in U material make experimental investigation and computational simulations of these materials challenging.

Recently, uranium disulfide (β -US2), as a member of the class of strongly correlated materials, has been extensively studied experimentally because of its structural and magnetic properties.[2– 7] Suski et al.[2] investigated the crystal structure of β -US2 by using single crystal x-ray diffraction. Tateiwa et al.[3] measured the magnetization of β -US2 under high pressure by piston cylinder and indenter-type cells in a superconducting quantum interference device (SQUID) magnetometer. Metoki and Ikeda, [4] and Metoki et al.[5] studied the metal– insulator crossover in β -US2 by using spin polarized neutron scattering. Ikeda et al.[6] performed a high pressure study to investigate the insulator– semimetal transition in β -US2. Yamamoto et al.[7] studied the magnetic behavior of β -US2 based on the magnetic polaron model.

However, to our knowledge, some of the ground-state properties of β -US2 are still unclear or under debate, and no data for phonon spectrum are available from the literature. As is well known, the accurate determination of phonon-dispersion curves is considered  as  an important reference for understanding its wide variety of physical properties of solids, such as: infrared, Raman, vibrational entropy, specific heats, Helmholtz free energy, internal energy, thermal expansion, constant volume heat capacity, lattice thermal conduction, and phenomena relating to the electron– phonon interaction. As a matter of fact, their understanding in terms of phonons is considered to be one of the most powerful pieces of evidence that our current quantum picture of solids is correct.[8, 9] These wide interests require the theory and experiment to go hand in hand, and thus need reliable and accurate theoretical work.

Conventional density functional schemes that apply the local density approximation (LDA) or the generalized gradient approximation (GGA) fail to capture the localized characteristic of 5f electrons coming from the strong intra-atomic Coulomb interaction. One promising way to improve the drawback is the density functional theory (DFT) + U approach, in which the underestimation of the strong electron– electron interaction is corrected by the Hubbard U parameter. Recently, a wide variety of physical properties of the uranium hydride, oxides, nitrides and carbides have been correctly reproduced by using LDA + U or GGA + U calculations.[10– 13] However, systematic theoretical investigations of the structural, magnetic and thermodynamic properties of the orthorhombic phase of US2 (Pbnm, No.  62) are lacking. Consequently, according to the good performance of DFT + U approaches in describing the strong-correlation systems, we will carry out the present study on β -US2 to provide a comparison with the experimental data currently available from the literature.

In this paper, we first investigate the electronic structure and magnetic stability of β -US2 at the ground-state by using the first-principles approach to which the Hubbard parameter U and the spin-polarization are added. We will then calculate the charge– density difference in the (001) plane, the Bader charge analysis and the Born effective charges. In addition, optical-mode frequencies including Raman-active and the infrared-active modes at Γ point are discussed in detail. The thermodynamic functions, such as Δ F, Δ E, CV, and S, are predicted in a range from 0  K to 1000  K.

The rest of the present paper is organized as follows. In Section 2, we introduce the theoretical framework and details of our calculations. In Section 3, we present and discuss the results of the electronic structure, chemical bonding, and thermodynamic properties of β -US2. In Section 4, we summarize our main findings and draw some conclusions.

2. Computational method

In the present work, the calculations are performed by using the Vienna ab initio simulation package (VASP)[14] through employing the GGA (LDA) exchange and the projector augmented wave (PAW) method[15, 16] to treat the core. The parameters for GGA (LDA) + U are set to be U = 4.5  eV and J = 0.5  eV, based on generally accepted values in the literature, [17, 18] in VASP only their difference is meaningful, so the effective U is 4  eV. The uranium 5f36s26p66d17s2 and the sulfur 3s23p4 electrons are treated as valence electrons. The self-consistent calculations are considered to be converged when the calculated total energy converges to less than 10− 5  eV for all of the iterations. A kinetic energy cutoff of 550  eV is used for the set of plane waves, and the k-point meshes in the full Brillouin-zone (BZ) are sampled by 3 × 4 × 7 k-mesh, and obtained by using the Monkhorst– Pack (MP) method.[19] Both spin-unpolarized and spin-polarized calculations are performed in this study. In the antiferromagnetic (AFM) calculations, we use the collinear 1 − k AFM structure where the atomic spin moment is along the [001] direction.

The charge transfers between the uranium atoms and the sulfur atoms are determined by the Bader charge analysis, [20] which is based on the quantum theory of atoms in molecules (QTAIM). The Born effective charges are obtained not only to describe the change in macroscopic polarization but also to study the longitudinal optical (LO) and transverse optical (TO) splitting at Γ point. The phonon dispersions and phonon density of states (DOS) are calculated by using the linear-response method[21, 22] that is implemented in the Phonopy software package, [23] which is based on density-functional perturbation theory (DFPT).

3. Results and discussion
3.1. Crystal structure and magnetic properties

Orthorhombic US2 with the space Pbnm (a = 8.480  Å , b = 7.114  Å , and c = 4.121  Å ), also called β -US2, is a well known phase at room temperature. The unit cell is composed of four formula units (FU) with the uranium atoms in 4c (0.1228, 0.2477, 0.2500) Wyckoff sites, the sulfur atoms S1 in 4c (0.0664, 0.8561, 0.2500), and S2 in 4c (0.8338, 0.4710, 0.2500) Wyckoff sites, respectively (see Fig.  1).

Fig.  1. The crystal structure of β -US2. Green (big) balls stand for represent uranium atoms, and red (small) balls stand for refer to sulfur atoms.

Table  1 shows the calculated parameters for the non-magnetic (NM), ferromagnetic (FM), and AFM states of β -US2 by using GGA, LDA, GGA+ U, and LDA+ U methods. Both AFM and FM lattice constants from LDA+ U typically underestimate experimental results whereas GGA+ U overestimates the results. Root mean square (RMS) deviations in GGA+ U lattice constants are similar for FM (0.088  Å ) and AFM (0.088  Å ) states of β -US2, but slightly larger for FM (0.094  Å ) and AFM (0.095  Å ) states in LDA + U method. We do not report GGA (LDA) results for the RMS data because they fails to reach the right ground state for the strongly correlated system, which predicts β -US2 to be an incorrect conductor.

The values of relative total energy Erel. (eV per β -US2) for the states of NM, FM, and AFM phases are calculated as listed in Table  1. We find that the total energies of the NM phase are both the highest in the GGA (LDA) scheme with and without Coulomb interaction; in other words, the NM phase is unstable for β -US2. According to the small value of total energy difference Δ E between FM and AFM states within the GGA (LDA)+ U approaches, β -US2 is expected to have a paramagnetic phase, [24] and the FM and AFM states could be degenerate, which is consistent with the available experimental results.[6]

Table 1. Calculated and experimental results for β -US2: optimized lattice constants, total magnetic moment μ tot, and band gaps Δ . Calculated relative energy Erel. (eV per β -US2) for NM, FM, and AFM Pbnm β -US2.

Overall, comparing our theoretical predictions with the experimental results, the accuracy of our atomic-structure and band-gap prediction for β -US2 is found to be quite satisfactory by tuning the effective Hubbard parameter within the GGA+ U approach of the AFM phase (the paramagnetic phase is unavailable in the present code), which supplies the safeguard for our further study of the electronic properties and chemical bonding nature of β -US2.

3.2. Electronic properties: Band structure and density of states

The calculated band structures of β -US2 along Γ -Y-T-Z-Γ -X-S-R-U directions in the full BZ are shown in Fig.  2. Here, the high-symmetry points correspond to Γ (0, 0, 0), Y(1/2, 0, 0), T(0, 1/2, 1/2), Z(0, 0, 1/2), S(1/2, 1/2, 0), X(0, 1/2, 0), R(1/2, 1/2, 1/2), and U(1/2, 0, 1/2). The Fermi energy is assumed to be at a zero level. Figure  2 shows a direct band gap with a width of 0.9  eV at U = 4.5  eV within GGA+ U approach, which is well consistent with the available experimental value of 1.2  eV. The first valence bands are presented in an energy region from 5.3  eV to Fermi energy level. The second valence bands are located at 11  eV below the Fermi energy level, with a width of about 2.5  eV (which is not shown in Fig.  2).

Fig.  2. Calculated band structure for β -US2 by using GGA+ U. The Fermi level is at 0  eV.

The total densities of states (TDOSs) and their corresponding partial densities of states (PDOSs) of U and S atoms for β -US2 are shown in Fig.  3. We can see that the d orbitals and f orbitals of U atom contribute less to their valence bands, while the f orbitals of U atom mainly contribute to the conduction bands. The upper valence band is mainly contributed from S-3p orbital with an admixture of U-5f orbital, revealing that a hybridization between the U and S atoms ranges from the − 1.5  eV to − 3.5  eV. The U-6d states also make some contributions to the hybridization. However, the hybridization between U-5f and the S-3p is weak, indicating that more ionicity character exists in the bonds. This feature can also be confirmed by following chemical bonding analysis.

Fig.  3. Calculated total density of states (TDOSs) and partial density of states (PDOSs) for β -US2 by using GGA+ U. The Fermi level is at 0  eV.

3.3. Chemical bonding

In order to analyze the U– S bonding of β -US2, we plot the charge– density contour maps (in units of e/Å 3) along the (001) plane, as shown in Fig.  4(a). For each U atom, the charge is the sum of the charges of 14 electrons outside the core of the PAW potential and the core states are occupied by 78 electrons. It can be clearly seen that the highest density charge piles up in the immediate vicinity of the nuclei, while the interstitial charge densities are relatively low. This reflects that most of the electrons are firmly bound up around the atomic nuclei and only a few valence electrons can escape from their bondage.

Fig.  4. Calculated (a) charge density and (b) charge density difference contour plots from the GGA + U calculation for β -US2 (in the units of e/Å 3) alone the (001) plane.

To understand the extent of charge transfer accompanying the formation of uranium chalcogenide compounds, we also plot the charge density difference contour maps by the following equation:[25]

where ρ is the valence-electron charge density. The result in the (001) plane is displayed in Fig.  4(b), the blue zone and orange zone represent the loss of charge and the gain of charge, respectively. For each calculation, we use the 2 × 2 × 1 supercell with the nuclear positions and lattice parameters fixed at the same values. By examining the plotted actual charge– density difference it is found that there is net charge transfer from the U atom to the S atom, while there is also obvious charge accumulation in the interstitial regions of U and S atoms. Thus, the U– S bond can be described as a mixture of covalent and ionic components. Moreover, one can also see that there is more charge transfer from U to S1 than from U to S2, which indicates that the ionic character of U– S1 is stronger than U– S2.

Combined with the orbital-resolved PDOSs shown in Fig.  2, we find that the ionicity character of the U– S bond can be attributed to the charge transfer from U-5f and U-6d states to S-3p states, and the covalent character of the U– S bond is associated with the hybridization between U-5f and S-3p states.[26, 27]

Table 2. Calculated Bader charges (QB) and Bader volumes (VB) for AFM/FM β -US2 by GGA+ U.

To further quantify the charge transfer between the U atom and the S atom, we perform a Bader charge analysis[28] of the charge density. In this calculation, we use a 128 × 108 × 64 charge density grid for the unit cell. The competition between the ionic character and covalent character in β -US2 can be related to the charge transfer between U atom and S atom. From Table  2, we can find that each U atom loses 2.14 |e|, while a charge of 1.10 |e| is transferred to S1 atom and 1.04 |e| transfer to S2 atom. These estimates suggest that any directional bonding of the S atom to U atom is ionic and small. Meanwhile, the results illustrate that the S1 atoms in β -US2 are easier to gain electrons than S2 atoms; in other words, the ionic character of U– S1 is stronger than U– S2.

Furthermore, we also calculate the Born effective charges to describe the charge in macroscopic polarization that is created by collective atomic displacements. In Table  3, is the j-th eigenvalue of symmetric part of the Z* tensor and Z̄ is the average of eigenvalue. The Born effective charges of S1 (− 2.80  a.u.) is very close to its nominal ionic valence charge (− 2  a.u.) and, therefore, U– S1 is considered to have almost the ionic character, which is similar to the result of charge– density difference and Bader charge analysis as mentioned above.

Table 3. Born effective charges of β -US2.

By comparing the charge– density difference, the Bader charge analysis and the Born effective charge for β -US2, we can find that: (i) mixtures of covalent and ionic character are present in both U– S1 bond and U– S2 bond, but the ionic character is slightly stronger than the covalent character, and when compared with scenario of U– S2 bond, the ionicity character of the U– S1 bond is slightly stronger than covalent character; and, (ii) the ionic charges for AFM and FM β -US2 can both be represented as by GGA + U calculations.

3.4. Phonon and thermodynamic properties

The phonon spectrum is closely associated with the dynamic stability, lattice thermal conduction, and thermodynamic properties of solid at finite temperature. In this work, the phonon spectra of the β -US2 are calculated by density-functional perturbation theory (DFPT) with GGA + U scheme for its AFM state. The calculated phonon dispersion curves and phonon DOS are plotted in Fig.  5.

Fig.  5. The calculated phonon dispersion curves by LO– TO splitting β -US2. (a) phonon dispersion curves and (b) phonon TDOS and PPDOS.

As shown in Fig.  1, each unit cell of β -US2 contains 12 atoms. Therefore, this system contains 36 normal modes, three of them are in the acoustic modes and the remainders are in optical modes. Since the space group of β -US2 is Pnma (No.  62), the corresponding point group is D2h (mmm). Based on the group-theoretical analysis, the irreducible representations of the vibrational modes in the center of the BZ can be expressed as follows:

Among them, 12 modes (2B1u, 5B2u and 5B3u) are infrared active, 18 modes (6Ag, 6B1g, 3B2g, and 3B3g) are Raman active, while the remaining three optical modes (3Au) are Silent modes.

In order to investigate the polarization effects of β -US2, we calculate the macroscopic static dielectronic tensor (including local field effects in DFT) and the Born effective charge tensor to correctly account for the longitudinal optical (LO)-transverse optical (TO) splitting at the Γ point for each nonequivalent atom based on DFPT. The calculated diagonal elements of the macroscopic static dielectric tensor are , , and , respectively.

The calculated phonon dispersion curves of Pbnm phase along high symmetry points in the BZ and the corresponding phonon DOS are shown in Fig.  5. We can see that the calculated phonon dispersion curves have no soft mode in the whole Brillouin zone at ambient pressure and 0  K, which indicates that β -US2 is dynamically stable.

Figure  5(b) also shows the PPDOSs projected onto U, S1, and S2 atoms. Owing to the fact that the U atom is heavier than the S atom, the vibration frequency of the U atom is lower than that of the S atom. Therefore, a gap exists between the optic branch and the acoustic branch. In the overall view of Fig.  5(b), one can find that there are three frequency ranges: the lowest part is from 0  THz to 4.1  THz, which is main contribution coming from the U atom; the middle part is from 4.4  THz to 7.0  THz dominated by the S2 atom; and, the highest part is from 7.0  THz to 10.0  THz, which is strongly related to the S1 atom.

The calculated phonon frequencies at the Γ point are listed in Table  4, including Infrared, Raman, and Silent active modes with LO– TO splitting. It is commonly believed that the LO– TO splittings are different for all modes, only the Infrared-active modes show the largest TO– LO splitting, while Raman and Silent active modes do correspond to modes of small or zero LO– TO splitting.[29] The results of our calculation also indicate that the LO– TO splittings of Infraredactive modes are apparent but there is no splitting in the Raman active mode nor Silent active mode. Since the B1u mode has displacement along the z axis, B2u mode has displacement along the y axis, the LO– TO splitting for displacement parallel to z-principal axis occurs for the B1u mode and displacement parallel to y axis occurs for the B2u mode. Large frequency splittings occur in B1u (144.7  cm− 1– 220.6  cm− 1) and B2u (194.1  cm− 1– 245.7  cm− 1) modes, which suggests that they involve large effective charges and make large contributions to the static dielectric tensor. The apparent LO– TO splitting indicates that β -US2 is a polar material.

Table 4. Optical phonon frequencies (in unit cm− 1) and LO– TO splitting for infrared active modes at Γ point of β -US2. R represents Raman active, IR denotes infrared active. The first column (e = 0) is for no electric field, the e ∥ x, e ∥ y, and e ∥ z are for the fields parrallel to x, y, and z principal axis, respectively.

Based on phonon DOS, the thermodynamic properties, such as the phonon contributions to the internal energy Δ E, the Helmholtz free energy Δ F, entropy S, and the constant-volume specific heat capacity CV, can be obtained by using the standard quasiharmonic approximation.[30] Within the approximation, the Δ E, Δ F, S, and CV can be given through

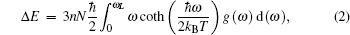
and

respectively.

Where kB and ħ are the Boltzman constant and the number of atoms per unit cell, respectively; ω is the phonon frequencies; N is the number of unit cell; and, g(ω ) is the normalized phonon DOS.

The curves of calculated internal energy Δ E, the Helmholtz free energy Δ F, the entropyS and the constant-volume specific heat CV versus temperature in a range from 0  K to 1000  K are shown in Fig.  6. The variation of CV with temperature obeys the Debye T3 law at low temperature, while over 500  K, CV they are close to the classic limit (which is called Dulong– Petit’ s law). To our knowledge, experimental and theoretical studies of the thermodynamic properties of β -US2 have not been found. Thus we hope that our results can guide future experimental investigations on the thermodynamic properties of β -US2

Fig.  6. Calculated thermodynamic properties of β -US2. (a) the internal energy Δ E, (b) the Helmholtz free energy Δ F, (c) the entropy S, (d) the constant-volume specific heat CV.

4. Conclusions

In this work, we present systematic studies of the electronic structure, chemical bonding, and thermodynamic properties of β -US2 in its orthorhombic lattice by using first-principles calculation with the LDA, GGA, LDA + U, and GGA + U approaches. By comparing with available experimental results, we find that Coulomb repulsion is vitally important. The correct ground-states of the paramagnetic phase β -US2 reported in experiments[6] are successfully reached by the GGA + U method. The calculations begin with the optimization for the lattice parameters and atomic coordinates. The results show that the calculated structural parameters and atomic coordinates are consistent with the experimental values. The calculated band structure and DOS indicate that β -US2 is a direct gap semiconductor with a wide gap of 0.9  eV.

On the basis of the electronic structure investigations, we also carry out systematic studies of chemical bonding and the dynamical properties of β -US2. By investigating the charge density differences, the Bader charge and the Born effective charges, we find that both U– S1 and U– S2 bond can be described as a mixture of covalent and ionic components but the ionic character is stronger than covalent character. The ionicity character of the U– S1 bond is slightly stronger than that of the U-S2 bond. The Raman and infrared active frequencies are assigned and presented. In particular, the infrared active modes are discussed in detail by LO– TO splitting. We can observe three giant LO– TO splittings occurring in B1u, B2u, and B3u modes. Finally, the thermodynamic properties are studied, such as Δ F, Δ E, CV, and S in temperatures ranging from 0  K to 1000  K within the harmonic approximation. We expect that our work can provide some valuable information about uranium chalcogenide compound materials that can be used for further experimental investigations.

Acknowledgment

The authors are grateful to the Center of High Performance Computing at the physics discipline of Sichuan University for their assistance with our computing needs.

Reference
1 Kohlmann H and Beck H P 1997 Z. Anorg. Allg. Chem. 632 785 [Cited within:1]
2 Suski W, Gibiński T, Wojakowski A and Czopnik A 1972 Phys. Stat. Solidi 9 653 DOI:10.1002/(ISSN)1521-396X [Cited within:3]
3 Tateiwa N, Haga Y, Sakai H, Ikeda S, Matsuda T D, Yamamoto E and Onuki Y 2011 J. Phys. Soc. Jpn. 80SA 103 DOI:10.1143/JPSJS.80SA.SA103 [Cited within:2]
4 Metoki N and Ikeda S 2013 J. Korean Phys. Soc. 62 1782 DOI:10.3938/jkps.62.1782 [Cited within:1]
5 Metoki N, Sakai H, Suzuki M, Yamamoto E, Haga Y, Matsuda T D and Ikeda S 2014 J. Phys. Soc. Jpn. 3 013011 [Cited within:1]
6 Ikedaa S, Sakaia H, Matsudaa T D, Tateiwaa N, Nakamuraa A, Yamamotoa E, Aokib D, Hommab Y, Shiokawab Y, Hedoc M, Uwatokoc Y, Hagac Y and Ounki Y 2008 Physica B 403 893 DOI:10.1016/j.physb.2007.10.059 [Cited within:3]
7 Yamamoto E, Tateiwa N, Haga Y, Ikeda S, Sakai H, Onuki Y and Fisk Z 2014 J. Phys. Soc. Jpn. 3 011095 [Cited within:2]
8 Yu Y, Zhou J J, Han H L, Zhang C Y, Cai T, Song C Q and Gao T 2009 J. Alloys Compd. 471 492 DOI:10.1016/j.jallcom.2008.04.039 [Cited within:1]
9 Baroni S, Gironcoli S D, Corso A D and Giannozzi P 2001 Rev. Mod. Phys. 73 515 DOI:10.1103/RevModPhys.73.515 [Cited within:1]
10 Zhang Y, Wang B T, Lu Y, Yang Y and Zhang P 2012 J. Nucl. Mater. 430 137 DOI:10.1016/j.jnucmat.2012.07.002 [Cited within:1]
11 Wang B T, Zhang P, Lizarraga R, Marco I D and Eriksson O 2013 Phys. Rev. B 88 104107 DOI:10.1103/PhysRevB.88.104107 [Cited within:1]
12 Lu Y, Wang B T, Li R W, Shi H L and Zhang P 2010 J. Nucl. Mater. 406 218 DOI:10.1016/j.jnucmat.2010.08.026 [Cited within:1]
13 Shi H L, Zhang P, Li S S, Sun B and Wang B T 2009 Phys. Lett. A 373 3577 DOI:10.1016/j.physleta.2009.07.074 [Cited within:1]
14 Kresse G and Hafner J 1993 Phys. Rev. B 47 558 DOI:10.1103/PhysRevB.47.558 [Cited within:1]
15 Bloechl P E 1994 Phys. Rev. B 50 17953 DOI:10.1103/PhysRevB.50.17953 [Cited within:1]
16 Kresse G and Joubert D 1999 Phys. Rev. B 59 1758 [Cited within:1]
17 Wang B T, Shi H, Li W and Zhang P 2010 Phys. Rev. B 81 045119 DOI:10.1103/PhysRevB.81.045119 [Cited within:1]
18 Wen X D, Martin R L, Scuseria G E, Rudin S P, Batista E R and Burrell A K 2013 J. Phys. : Condens. Matter 25 025501 DOI:10.1088/0953-8984/25/2/025501 [Cited within:1]
19 Monkhorst H J and Pack J D 1976 Phys. Rev. B 13 5188 DOI:10.1103/PhysRevB.13.5188 [Cited within:1]
20 Bader R F W 1990 Atoms in molecules: a uantum theory New York Oxford University Press [Cited within:1]
21 Giannozzi P and de Gironcoli S 1991 Phys. Rev. B 43 7231 DOI:10.1103/PhysRevB.43.7231 [Cited within:1]
22 Gonze X and Lee C 1997 Phys. Rev. B 55 10355 DOI:10.1103/PhysRevB.55.10355 [Cited within:1]
23 Togo A, Oba F and Tanaka I 2008 Phys. Rev. B 78 134106 DOI:10.1103/PhysRevB.78.134106 [Cited within:1]
24 Huang L F, Zheng X H, Zhang G R, Li L L and Zeng Z 2011 J. Phys. Chem. C 115 21088 DOI:10.1021/jp208067y [Cited within:1]
25 Hector L G, Herbst J F and Capehart T W 2003 J. Alloys Compd. 353 74 DOI:10.1016/S0925-8388(02)01324-5 [Cited within:1]
26 Wang B T, Shi H L, Li W D and Zhang P 2010 Phys. Rev. B 81 045119 DOI:10.1103/PhysRevB.81.045119 [Cited within:1]
27 Andersson D A, Lezama J, Uberuaga B P, Deo C and Conradson S D 2009 Phys. Rev. B 79 024110 DOI:10.1103/PhysRevB.79.024110 [Cited within:1]
28 Tang W, Sanville E and Henkelman G 2009 J. Phys. : Condens. Matter 21 084204 DOI:10.1088/0953-8984/21/8/084204 [Cited within:1]
29 Iliev M N, Lee H G, Popov V N, Abrashev M V, Hamed A, Meng R L and Chu C W 1997 Phys. Rev. B 56 2488 DOI:10.1103/PhysRevB.56.2488 [Cited within:1]
30 Siegel A, Parlinski K and Wdowik U D 2006 Phys. Rev. B 74 104116 DOI:10.1103/PhysRevB.74.104116 [Cited within:1]