Cite this Article
Li Ying, Sun Min-Na, Zhang Jin-Jun†, Pan Jun-Xing, Guo Yu-Qi, Wang Bao-Feng, Wu Hai-Shun. Multiple patterns of diblock copolymer confined in irregular geometries with soft surface. Chinese Physics B, 24(12): 126403  
Permissions
Multiple patterns of diblock copolymer confined in irregular geometries with soft surface
Li Ying, Sun Min-Na, Zhang Jin-Jun†, Pan Jun-Xing, Guo Yu-Qi, Wang Bao-Feng, Wu Hai-Shun
School of Chemistry and Materials Science, Shanxi Normal University, Linfen 041004, China

†Corresponding author. E-mail: zhangjinjun@sxnu.edu.cn

*Project supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20121404110004), the Research Foundation for Excellent Talents of Shanxi Provincial Department of Human Resources and Social Security, China, and the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi Province, China.

Abstract

The different confinement shapes can induce the formation of various interesting and novel morphologies, which might inspire potential applications of materials. In this paper, we study the directed self-assembly of diblock copolymer confined in irregular geometries with a soft surface by using self-consistent field theory. Two types of confinement geometries are considered, namely, one is the concave pore with one groove and the other is the concave pore with two grooves. We obtain more novel and different structures which could not be produced in other two-dimensional (2D) confinements. Comparing these new structures with those obtained in regular square confinement, we find that the range of ordered lamellae is enlarged and the range of disordered structure is narrowed down under the concave pore confinement. We also compare the different structures obtained under the two types of confinement geometries, the results show that the effect of confinement would increase, which might induce the diblock copolymer to form novel structures. We construct the phase diagram as a function of the fraction of B block and the ratio of h/ L of the groove. The simulation reveals that the wetting effect of brushes and the shape of confinement geometries play important roles in determining the morphologies of the system. Our results improve the applications in the directed self-assembly of diblock copolymer for fabricating the irregular structures.

PACS: 64.75.Gh; 64.75.Yz; 64.70.km
Keyword: self-assembly; irregular geometries; soft confinement; self-consistent field
1. Introduction

Block copolymers can form a rich variety of novel and new structures, these structures have potential applications, for example, photonic crystals, lithographic templates for nanowires, high-density magnetic storage media, and drug delivery.[1, 2] So the self-assembly of block copolymer systems has attracted a great deal of attention in recent years. The simplest block copolymer is a diblock copolymer, which can self-assemble into cylinders, lamellae, spheres, and gyroid structures depending on the block volume fractions and the repulsive interactions between the different blocks.[3] We can put block copolymers into geometries, which can add the parameters to control their phase behaviors, such as the interaction between the confined surface and the block copolymers, which can make the block copolymers rebalance between the entropy and energy, [2, 4, 5] and affect the self-assembly of the block copolymers, as previously demonstrated in a linear AB diblock copolymer.[2, 6] The AB linear diblock copolymer is the best example of being enforced into various confinement geometries.[7] The computational modeling to describe polymer morphology is now widespread, [8] such as the self-consistent field theory (SCFT), [9– 12] and the cell dynamics simulation method (CDS).[13– 15] In previous years, studies mostly have focused on thin films about the confinement effect for one-dimensional (1D) confinement.[16– 23] In experimental studies, Koneripalli et al.[24] studied the symmetric poly(ethylenepropy1ene)-poly-(ethylethylene) (PEP-PEE) diblock copolymer confined between two solid surfaces and found that the lamellae phase was always parallel to the surface, which was in accordance with the theoretical studies of Shull.[25] For two-dimensional (2D) confinement, in experimental studies, Xiang et al.[26] investigated both the symmetric and asymmetric polystyrene-b-polybutadiene (PS-b-PBD) block copolymers under cylindrical confinement and found that the results were in qualitative agreement with the simulation results investigated by Li et al.[27] The self-consistent field theory was used to study the microstructures from confined asymmetric diblock copolymer, and the Monte Carlo method was adopted to investigate the symmetric diblock copolymer under cylindrical confinement, and many novel structures were obtained by changing the ratio between the pore diameter and the bulk period (D/L).[28– 30] For three-dimensional (3D) confinement, Chen and Liang studied the self-assembly of asymmetric diblock copolymer under spherical confinement, and observed many new structures that were different from those observed in 1D or 2D confinement.[31] In order to fully study the two-dimensionally confined system, Yu et al. studied diblock copolymer confined in channels of various shaped cross sections, including regular triangle, rectangle, square, regular hexagon, and ellipse. They found that the shape and size of the confinement geometries had a great effect on the morphologies of the block copolymers.[32, 33] Tang and Ma investigated the directed self-assembly of block copolymers on 2D sparse rectangle lattice template and pointed out that the template spacings could modulate the local spacings and the orientation of the block copolymer microdomains.[34] Above these studies mostly focused on regular confinement geometries, there are few studies about irregular confinement geometries. In addition, the confinement geometries used in the experiment are not always regular. Thus, we should study the block copolymers confined in irregular geometries.

Tuning the interfacial energies between block copolymers and the confined surface is extremely important, which can enhance the mechanical, electronic, and photonic properties of materials.[35– 41] An effective way to modify the interfacial energies is to graft polymers on the confined surfaces, which is widely used now. The polymer chains are grafted by one end to a solid surface and stretched away from the surface, forming a polymer “ brush” .[42] Polymer brushes can change surface properties including adhesion and wetting behaviors. For grafted polymer systems, the theoretical research methods have developed rapidly, which include self-consistent field theory, [43, 44] analytical theories, [45– 47] and Monte Carlo simulations.[48, 49] Xie et al. simulated the hard and soft confinement effects on the glass transition of polymers confined in nanopores, and found the two confined surfaces had fundamentally different properties.[50] Ren et al. studied the morphologies of asymmetric diblock copolymer confined between polymer-grafted surfaces and pointed out that due to the interfacial affinity and the interaction between the entropy effects of stretched brushes, the reentrant structures varied from the lamellar to hexagonal phases, and also found the structural frustration could be relieved by being out of shape of the polymer brush surface in contrast to the hard-wall cases.[51] They also studied the phase behaviors of colloid-polymer mixtures confined between two soft surfaces and found that the brush-mediated interaction played an important role in the self-assembly of colloid.[52] Li and Zhu pointed out that the effect of the entropic elasticity of polymer brushes played an important role in controlling the morphology of the diblock copolymer confined in a cylindrical nanopore with polymergrafted surface.[53] The development of the experiment has also made significant progress. Tang et al. successfully synthesized polymer brushes by combining ring-opening polymerization with living anionic polymerization.[54]

Inspired by these studies, we study the self-assembly and construct phase diagram of the diblock copolymer confined in irregular geometries with soft surface by using SCFT, which has proven to be a successful theory for predicting the morphologies.[55, 56] The rest of this paper is arranged as follows. In Section 2, the model and the SCFT method are introduced. In Section 3, we mainly discuss the shapes of confinement geometries, the fraction of B block, the heights and the widths of grooves on the morphologies of diblock copolymer and some conclusions are drawn from the present study in Section 4.

2. Model and method

We consider an incompressible melt of nco AB diblock copolymer confined in irregular geometries with the surface grafted by nbr A-type homopolymer chains. The cross section of the irregular geometries is a concave pore, which is set in the x– y plane. Both diblock copolymer and homopolymer chains consist of N segments of length a and the length is expressed in units of the radius of gyration, Rg, of the polymer. The fractions of A and B monomer in a copolymer chain are denoted by fi (i = A, B) (0 ≤ fi ≤ 1) and each segment has a fixed volume 1/ρ . The grafting density is defined as σ 1 = nbr/2(Lx + Ly + h) for a concave pore with one groove and σ 2 = nbr/2(Lx + Ly + 2h) for a concave pore with two grooves. For the diblock copolymer melt confined in irregular geometries with volume V, the free energy F can be obtained as follows:

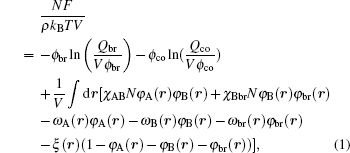
where kB is the Boltzmann constant and T is the temperature. The free energies come from the entropic and energetic contributions. The entropic part originates from the configurations of A block, B block, and brush in the mean fields, which can be obviously affected by the confinement geometries. The energetic part originates from the repulse interactions between blocks and brushes. The Flory– Huggins interaction parameters are expressed by χ ij (i, j = A, B, brush), φ A, φ B, and φ br are local volume fractions of A segment, B segment and brush, ω A, ω B, and ω br are the mean fields of monomer blocks and sing brush that are produced by the surrounding chains, ϕ co and ϕ br are the average volume fractions of the diblock copolymer and the brushes, ϕ co = ncoNρ − 1/V and ϕ br = nbrNρ − 1/V. ξ (r) is a Lagrange multiplier to ensure the incompressibility of the system. Qco = ∫ drq(r, s) q+ (r, s) and are single-chain partition functions of diblock copolymer and homopolymer brushes in the mean fields. The end-segment distribution function q(r, s) is the probability that a polymer chain segment of contour length s with a free chain end has its other end located at r. The chain propagators q(r, s) and its conjugate q+ (r, s) obey the following modified diffusion equations:

and

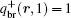
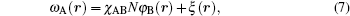
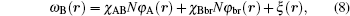
with ω (r, s) = ω A(r) for 0 ≤ s ≤ fA and ω (r, s) = ω B(r) for fA < s ≤ 1. The initial condition for copolymer is q(r, 0) = 1 and q+ (r, 1) = 1, and the initial condition for brushes is qbr(r = ri, 0) = 1 (qbr(r ≠ ri, 0) = 0, i = x, y) and , where rx presents positions of two planes at x = 1 and x = Lx and ry presents positions of two planes at y = 1 and y = Ly and the boundary of the irregular geometries which are shown in Fig.  1 is set to 1. Minimizing the free energy in Eq.  (1), with respect to the monomer densities and mean fields leads to the set of mean-field equations:

and

In our study, outside the irregular pore, there is no diblock copolymer, so we set the end-segment distribution functions to be 0. We focus on the case of the equal interactions among A, B, and brushes with χ ABN = χ BbrN = 20.0, the fraction of homopolymer chains is set to be fbr = 0.6 and the chain lengths of the diblock copolymer and homopolymer chains are both set to be N = 100. For our system, the calculation is performed in a lattice of (Lx × Ly) 100× 100, and the chain contour length for each block is discretized into 100 segments. We take fixed boundary conditions in our calculation. The calculation is started by using initial random value of the field, ω (r). The diffusion equations are solved by using the Crank– Nicholson scheme and the scheme has been proven under different confinement conditions.[57] The free energy can then be obtained by Eq.  (1), the volume fractions are evaluated by Eqs.  (4)– (6), and the fields are calculated by Eqs.  (7)– (9). Then updated fields are inputted into Eqs.  (2) and (3). All calculations are iterated until the free energy difference between two sequential steps is less than 10− 10. We should point out that the grafted chain ends are treated as being mobile on the substrate for computational efficiency.

3. Numerical results and discussion

For a bulk diblock copolymer melt, the phase behavior is controlled by two parameters, fi (i = A, B) and χ ABN. When the block copolymers confined in irregular geometries with soft surface, there are more parameters to control the patterns of diblock copolymer, such as the geometrical shape of confinement. In this paper, we focus on the effects of the shape of confinement geometries, the fraction of B block, the height, and the width of grooves on the morphologies of diblock copolymer, and neglect the effect of grafting density, due to the small changes, on the morphology of diblock copolymer. Through changing the confinement geometries, the heights, and the widths of grooves, we obtain a series of structures. Two types of confinement geometries are considered as shown in Fig.  1. The schematic diagram of a concave pore with one groove is shown in Fig.  1(a), and the schematic diagram of a concave pore with two grooves is shown in Fig.  1(b), where h is the height of the groove, L is the width of the groove, Lx and Ly are the length and width of the irregular geometry. In this paper, we consider the internal surface of the schematic diagram of Fig.  1, which is grafted by A-type homopolymer chains. In addition, it is worth mentioning that the blue color represents the morphologies of the brush and A block and the red color refers to the morphology of B block in our paper.

Fig.  1. Schematics of the shapes of confinement geometries of (a) concave pore with one groove and (b) concave pore with two grooves.

3.1. Morphology of diblock copolymer confined in concave pore
3.1.1. Effect of the fraction of B block on morphology of the diblock copolymer

We first change the fraction of B block to observe the patterns of the diblock copolymer confined in a concave pore with h = 4.92Rg and L = 4.92Rg. In Fig.  2, we can see that the B block forms cylinders and lamellae, and finally the A block forms cylinders dispersed in the B domain with increasing the fraction of the B block. Because the surface of the concave pore is grafted by A-type homopolymer chains, the A component forms structures around the concave pore. In Fig.  2(a), the major A component provides a background where the minority B component forms the cylinders when fB = 0.25. In Fig.  2(b), when fB = 0.45, B block forms one lamellae along the edge of the concave pore and another one parallel lamellae in the center of the concave pore. Figure 2(c) shows one concentric lamellae formed by the B block in the center of the concave pore besides one lamellae along the edge of the concave pore with fB = 0.5. This is because the lamellar structures are formed when the two blocks have equal lengths. In contrast, increasing the fraction of B block, the A block starts to form cylindrical structures and B block provides a background. When fB = 0.65, hexagonal structures are formed by A block and dispersed in the B domain as shown in Fig.  2(d). While the fraction of the B component increases to 0.75, the A block forms tetragonal structures where the B block provides a background as shown in Fig.  2(f). From simulation results, first, we can conclude that the asymmetric diblock copolymer can form cylindrical structures of the minor component, which are dispersed in the major component. While the symmetric diblock copolymer can self-assemble into lamellar structures under the concave pore, which is similar to what the diblock copolymer in an unconfined system and a regular geometrical confinement system do. Second, the most outstanding characteristic is that the top layer cylinders are deviously arranged and the top layer lamellae is arranged parallelly to the groove due to the effect of curvature.

Fig.  2. Morphologies of diblock copolymer as a function of the volume fraction of B block with h = 4.92Rg and L = 4.92Rg. The blue color represents the morphologies of A block and the brush, the red color refers to the morphology of B block. (a) fB = 0.25, (b) fB = 0.45, (c) fB = 0.5, (d) fB = 0.65, (e) fB = 0.72, (f) fB = 0.75.

3.1.2. Differences in diblock copolymer between concave pore confinement and regular square confinement

Diblock copolymer can self-assemble into cylinders, lamellae and spheres and gyroid structures, whether the diblock copolymer is confined in a regular square or in a concave pore. In order to study the differences between regular square confinement and concave pore confinement, and study the effect of the height of the groove on the morphologies of diblock copolymer, we take fB = 0.65 for example due to the more clear diversities of structures, which are shown in Fig.  3. We can clearly see that the major B component provides a background where the minor A component forms cylinders or lamellar structures. First, the morphology of the A block is disorderly arranged under regular square confinement as shown in Fig.  3(a), while it can be seen from Figs.  3(b)– 3(e) that the A block forms different structures when diblock copolymer is confined in a concave pore with increasing the height of the groove, the morphology of A block changes from the hexagonal cylinders to the lamellar structures and finally to the trigonal cylinders. This is because the diblock copolymer is confined in a concave pore, the increase of interfacial areas results in the increase of interfacial energies, which induces the interaction between homopolymer brushes and the diblock copolymer to increase, so in order to reduce the energies, the structures of the A block are orderly arranged. Compared with the morphologies in Fig.  3(b), fewer cylinders can be accommodated in Fig.  3(e) due to the effect of the groove. In addition, the first layer cylindrical structures curve along the groove because of the effect of curvature of diblock copolymer under concave pore confinement, while in regular square confinement, there is no curvature, so the structures are squarely arranged.

Fig.  3. The morphologies of diblock copolymer confined in a regular square and in a concave pore with fB = 0.65 and the fixed L = 4.92Rg: (a) regular square, (b) h = 2.46Rg, (c) h = 4.92Rg, (d) h = 7.38Rg, (e) h = 9.84Rg.

To systematically study the differences between the regular square confinement and the concave pore confinement, we investigate the phase transition between cylinder and lamellae, which is plotted as a function of the volume fraction of the B block as shown in Fig.  4. Figure  4(a) shows the phase stability regions as a function of the fraction of the B monomer in regular square confinement, and figure  4(b) shows the phase stability regions as a function of the fraction of B monomer in concave pore confinement with h = 7.38Rg and L = 4.92Rg. First, we can see that the same feature is that the lengths of cylindrical structures and mixed cylinders and lamellae are formed by the B block in a regular square confinement, which is similar to those observed in diblock copolymer under the concave pore confinement. There are, however, significant differences between the two geometrical confinements. The most visible differences are the length of lamellae in a concave pore confinement is much longer than that in a regular square confinement and the length of mixed cylinder and lamellae that are formed by the A block in a concave pore confinement is much shorter than that in a regular square confinement, for example, diblock copolymer forms lamellar structures in the concave pore confinement and forms mixed cylinder and lamellae in the regular square confinement when fB = 0.65, which we can see in Figs.  3(a) and 3(d). This means when diblock copolymer is confined in a concave pore, we can obtain many ordered lamellae through tuning the height of the groove. The other feature that is the same is the lengths of cylinders are formed by the A block in concave pore confinement are almost like those in regular square confinement. We can obtain more ordered lamellae and less disordered structures in diblock copolymer within a concave pore than in a regular square confinement, and this can effectively improve the properties of materials and can inspire potential applications for the materials involved in irregular structures.

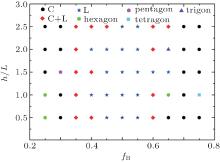
Fig.  4. Phase transitions with volume fraction of B block in regular square confinement and in concave pore confinement. The C and the L represent the cylindrical and the lamellar structures, respectively. (a) The phase stability regions of different morphologies in regular square confinement. (b) The phase stability regions of different morphologies in concave pore confinement with h = 7.38Rg and L = 4.92Rg.

3.1.3. Phase diagram of diblock copolymer confined in concave pore

To gain a comprehensive insight into the morphologies of diblock copolymer confined in a concave pore, we construct the phase diagram of the AB diblock copolymer as a function of the fraction of B block and the ratio of h/L of the groove in Fig.  5. When 0.45 ≤ fB ≤ 0.55, the morphology of diblock copolymer is of a mostly lamellar structure. When fB < 0.45 or fB > 0.55, the diblock copolymer forms the cylindrical or mixed cylindrical and lamellar structure, which is similar to the phase diagram of the diblock copolymer in bulk or in regular square confinement. There are, however, remarkable differences between them. First, our phase diagram includes more interesting structures such as the pentagonal, tetragonal, and trigonal cylinders, which do not exist in the phase diagram of the bulk system nor the regular square confinement system. Second, our phase diagram has less mixed cylindrical and lamellar structure than the phase diagram of the unconfined system and the regular square confinement system. These differences result from the diblock copolymer confined in irregular geometries, with the height of the groove increasing, fewer cylinders can be accommodated, so tetragonal and trigonal cylinders emerge. Another reason is that the increase of interfacial area results in the increase of interfacial energy, and the surfaces of irregular geometries graft A-type homopolymer chains, the new surface favors the A block, which can add extra interfacial energies to the free energy, so the diblock copolymer forms new ordered lamellae and cylinders in order to reduce the energies.

Fig.  5. Phase diagram of the AB diblock copolymer as a function of B monomer fraction fB and the ratio of h/L of the groove in concave pore confinement with the fixed L = 4.92Rg, the circle, diamond, star, hexagon, pentagon, square, and uptriangle represent the cylinders, mixture of cylinders and lamellae, lamellae, hexagon, pentagon, tetragon, and trigon, respectively.

The region of cylindrical structures is longer than the other ones with any volume fraction of B block when h/L = 0.5, and the region of lamellar structures is longer than other ones with any volume fraction of the B block when h/L = 1.5. This is because the height of groove h/L = 0.5 is small, which has little differences from the regular square, so the structures of the diblock copolymer under concave pore confinement are similar to those obtained in regular square confinement. Moreover, the height is moderate but not very big with h/L = 1.5, the effect of curvature impels the morphologies near the groove to be more flatter than the others. Those features can effectively control the structures and the properties of the materials. The trigonal cylinders are formed when fB = 0.65 and h/L = 2.0, the pentagonal cylinders are observed when fB = 0.3 and h/L = 1.5 and tetragonal cylinders are formed when fB = 0.75 and h/L = 1.0; those are because with increasing the groove fewer cylinders can be accommodated, and it is the result of the effect of curvature and the competition of the interfacial energies between the two blocks and the conformational entropy.

3.2. Morphologies of diblock copolymer confined in concave pore with two grooves

Next, we discuss the second type of confinement geometry, that is, the concave pore with two grooves, which is shown in Fig.  1(b). In this subsection, we obtain some new structures by changing the fraction of the B block and the heights and the widths of grooves.

3.2.1. Effect of the height of grooves on morphology of the diblock copolymer

First, we discuss the morphologies of diblock copolymer when we change the fraction of B block with h = 2.46Rg, which are shown in Figs.  6(a)– 6(c). It is very interesting that diblock copolymer is confined in the concave pore with two grooves. The most outstanding characteristic is that the morphologies of the top layer and the bottom layer are deviously arranged along the grooves, which can be seen in Fig.  6. When fB = 0.25, the B block forms hexagonal cylinders where the A block offers a background in Fig.  6(a). With increasing the fraction of the B block, when fB = 0.45, the B block forms two parallel lamellae within the irregular geometry and forms one curved square lamella along the edge of the irregular geometry in Fig.  6(b), owing to the fact that the diblock copolymer favors AB interfaces with low curvature being nearly equal volume fractions of the two blocks. When the volume fraction increases to 0.75, the A block forms a hexagonal structure dispersed in the B domain.

Then we discuss the morphologies of diblock copolymer when we change the fraction of B block with h = 4.92Rg as shown in Figs.  6(d)– 6(f). When fB = 0.25, the B domain is cylindrically distributed in Fig.  6(d). Because the increase of the height of grooves leads to the effect of confinement increasing, the number of cylinders in the middle of irregular geometry is less than that in Fig.  6(a). In Fig.  6(e), when fB = 0.45, the B block forms one parallel lamella in the middle of the irregular geometry and forms one more curved square lamella along the edge of the irregular geometry surface than that in Fig.  6(b) due to the effect of the high curvature and the strong confinement, while the A block forms one new structure in the interior of the irregular geometry, “ bone” . When the volume fraction increases to 0.75, tetragonal cylinders are observed and the B block provides a background in Fig.  6(f), which is different from that in Fig.  6(c) because the effect of the height of the groove resulting in fewer cylinders can be accommodated.

Fig.  6. (a)– (c) Morphologies of diblock copolymer by changing the fraction of B block with h = 2.46Rg and L = 1.23Rg; (d)– (f) morphologies of diblock copolymer by changing the fraction of B block with h = 4.92Rg and L = 1.23Rg. From left to right the fractions of B component are fB = 0.25, fB = 0.45, and fB = 0.75, respectively.

Comparing the morphologies in Figs.  6(a)– 6(c) with those in Figs.  6(d)– 6(f), we find that the top and the bottom layer structures are more curved in Figs.  6(d)– 6(f), because the increase of height of groove results in the effect of confinement and curvature increase and also leads to the increase of interface interaction between the surface of irregular geometry and diblock copolymer. This may inspire potential properties of many kinds of materials.

3.2.2. Effect of the width of groove on morphology of the diblock copolymer

Now, we take the phase ordered degree from fB = 0.5 to fB = 0.75 for example to investigate the effect of the width of groove on the morphology of the diblock copolymer in Fig.  7.

Fig.  7. Phase ordered degree of the diblock copolymer as a function of fB in a range from 0.5 to 0.75 and the ratio of h/L of groove with the fixed h = 4.92Rg. The lefttriangle represents ordered structure and the righttriangle represents disordered structure.

It is worth mentioning that the order phase includes cylinder, lamellae, and other structures which are regularly arranged and the disordered phase includes the structures which are randomly distributed. The most remarkable characteristic is that the phase ordered degree becomes better with the width of grooves increasing. Because the increase of the width of groove can induce the interfacial area to increase, which results in the increase of interfacial energy and also causes the interaction energy between homopolymer brushes and the copolymer to increase, in order to reduce the energy, the structures are orderly arranged, which is similar to that observed through changing the height of the groove. In Fig.  8, we take examples from the phase diagram to illustrate the phase ordered degree. We can see the morphologies of diblock copolymer are regularly arranged when fB = 0.5 in Fig.  8(a). When fB = 0.65 and h/L = 4, the structures are randomly distributed, while the structures are regularly arranged in the other two cases, which can be seen from Fig.  8(b). In addition, the effect of confinement increases with the width of groove increasing.

Fig.  8. (a) Morphologies of diblock copolymer by changing the width of groove with fB = 0.5 and the fixed h = 4.92Rg; (b) the morphologies of diblock copolymer by changing the width of groove with fB = 0.65 and the fixed h = 4.92Rg. From left to right the ratios of h/L of the groove are 4, 2.4, and 1, respectively.

3.2.3. Differences between the two types of irregular geometry confinements

In order to investigate the differences between the two types of irregular geometry confinements, we compare the patterns of diblock copolymer under the two types of confinement with fixed h = 4.92Rg and L = 4.92Rg as shown in Fig.  9. We can conclude that the shape of confinement geometries plays an important role in controlling the morphologies of AB diblock copolymer. Compared with the scenario of the concave pore confinement, the morphologies of concave pore with two grooves have great changes, such as when fB = 0.55, the concentric lamella formed by the B block is observed in the middle of the concave pore in Fig.  9(a), while the B block forms one new structure in Fig.  9(d), “ ladder” . In Fig.  9(b), when the diblock copolymer is confined in a concave pore, the A block forms disordered structures, in contrast, when diblock copolymer is confined in a concave pore with two grooves, the A block forms two parallel lamellae and two perpendicular lamellae in Fig.  9(e). When fB = 0.65, hexagonal cylinders are formed by the A block as shown in Fig.  9(c), meanwhile, the A block forms four perpendicular lamellar structures in Fig.  9(f). We attribute these to the increase of the effect of the confinement when the diblock copolymer is confined in the concave pore with two grooves, and the effect of the curvature makes the diblock copolymer form the morphologies which are different from those in concave pore confinement. In addition, in Figs.  9(d)– 9(f), we can see that the lamella orientation of the A block is inversed from the horizontal direction to the vertical direction with the fraction of B block increasing.

Fig.  9. The different morphologies of two irregular geometries confinement with h = 4.92Rg and L = 4.92Rg. From left to right the fractions of the B component are fB = 0.55, fB = 0.6, and fB = 0.65, respectively. When the diblock copolymer is confined in a concave pore, the morphologies of diblock copolymer as a function of fB are shown in panels (a)– (c); when the diblock copolymer is confined in a concave pore with two grooves, the morphologies of diblock copolymer as a function of fB are shown in panels  (d)– (f).

Comparing the two types of confinements, we can find some differences between them. First, when the diblock copolymer is confined in a concave pore, the top layer cylinders curve along the groove, while the diblock copolymer is confined in a concave pore with two grooves, the top and the bottom layer cylinders curve along the two grooves. The second characteristic is that certain structures have rotational symmetries in diblock copolymer under concave pore confinement, while most structures have both rotational symmetries and central symmetries when the diblock copolymer is confined in the concave pore with two grooves.

4. Conclusions

We perform an SCFT study on the self-assembly phase behaviors of diblock copolymer confined in irregular geometries with soft surface. Two types of confinements are considered, i.e., diblock copolymer confined in a concave pore and that in a concave pore with two grooves. The effect of confinement would increase, whether the width or the height of the groove increases, so a variety of interesting morphologies in various symmetries are observed. From this paper, some inspiring conclusions are obtained. First, when the diblock copolymer is confined in irregular geometry, we obtain more novel structures that cannot be observed in the bulk system nor in other 2D confinement because the confinement shapes are rather special. Second, the range of ordered lamellae formed by the diblock copolymer is enlarged and the range of disordered structure is narrowed down under the concave pore compared with that by the diblock copolymer under the regular square confinement, which might inspire potential applications of materials. Third, the cylinders near the grooves are deviously arranged along the grooves in the diblock copolymer under the irregular geometry confinement instead of the flat arrangement in regular confinement due to the effect of curvature. Fourth, the lamella orientation is inverted from the horizontal direction to the vertical direction by increasing the fraction of B block with h = 4.92Rg and L = 4.92Rg. This might provide an effective way to control the properties of materials. In addition, when the diblock copolymer is confined in a concave pore, certain structures have rotational symmetries, whereas most structures formed by the diblock copolymer have central symmetries except for rotational symmetries under a concave pore with two grooves. This observation indicates that the symmetry of structures formed by diblock copolymer is related to the shape of geometric confinement.

Our investigation show that for the diblock copolymer under irregular geometry with a soft surface, the morphology can be tuned by adjusting the shape of confinement geometry, the monomer fraction of the diblock copolymer, the height, and the width of groove. Our results are expected to inspire potential applications in the self-assembly of diblock copolymer for fabricating the irregular structures. For example, when the diblock copolymer is confined in a concave pore, the patterns have been widely employed in the keel of ceiling material in the home improvement building material industry and in the thermal insulation material in experiments.

Reference
1 Park C, Yoon J and Thomas E L 2003 Polymer 44 6725 DOI:10.1016/j.polymer.2003.08.011 [Cited within:1]
2 Shi A C and Li B H 2013 Soft Matter 9 1398 DOI:10.1039/C2SM27031E [Cited within:3]
3 Bates F S and Fredrickson G H 1999 Physics Today 52 32 DOI:10.1063/1.882522 [Cited within:1]
4 Stewart-Sloan C R and Thomas E L 2011 Eur. Polym. J. 47 630 DOI:10.1016/j.eurpolymj.2010.10.013 [Cited within:1]
5 Li S B, Qiu W J, Zhang L X and Liang H J 2012 J. Chem. Phys. 136 124906 DOI:10.1063/1.3697764 [Cited within:1]
6 Wyman I, Njikang G and Liu G J 2011 Prog. Polym. Sci. 36 1152 DOI:10.1016/j.progpolymsci.2011.04.005 [Cited within:1]
7 Tsarkova L, Knoll A, Krausch G and Magerle R 2006 Macromolecules 39 3608 DOI:10.1021/ma060224n [Cited within:1]
8 Ginzburg V V, Weinhold J D and Trefonas P 2015 J. Polym. Sci. Pol. Phys. 53 90 DOI:10.1002/polb.23365 [Cited within:1]
9 Tang Q Y and Ma Y Q 2009 J. Phys. Chem. B 113 10117 DOI:10.1021/jp901170x [Cited within:1]
10 Liu M J, Li S B, Zhang L X and Wang X H 2010 Chin. Phys. B 19 028101 DOI:10.1088/1674-1056/19/2/028101 [Cited within:1]
11 Li S B, Zhang L X, Wang X H and Liang H J 2011 Chin. Phys. B 20 083601 DOI:10.1088/1674-1056/20/8/083601 [Cited within:1]
12 Li W H and Wickham R A 2006 Macromolecules 39 8492 DOI:10.1021/ma061630+ [Cited within:1]
13 Sun M N, Zhang J J, Wang B F, Wu H S and Pan J X 2011 Phys. Rev. E 84 011802 [Cited within:1]
14 Pan J X, Zhang J J, Wang B F, Wu H S and Sun M N 2013 Chin. Phys. B 22 026401 DOI:10.1088/1674-1056/22/2/026401 [Cited within:1]
15 Zhang L C, Sun M N, Pan J J, Wang B F, Zhang J J and Wu H S 2013 Chin. Phys. B 22 096401 DOI:10.1088/1674-1056/22/9/096401 [Cited within:1]
16 Xu T, Hawker C J and Russell T P 2005 Macromolecule 38 2802 DOI:10.1021/ma048005u [Cited within:1]
17 Wang Q, Nealey P F and de Pablo J J 2001 Macromolecules 34 3458 DOI:10.1021/ma0018751 [Cited within:1]
18 Wang Q, Nealey P F and de Pablo J J 2003 Macromolecules 36 1731 DOI:10.1021/ma020996t [Cited within:1]
19 Horvat A, Lyakhova K S, Sevink G J A, Zvelindovsky A V and Magerle R 2004 J. Chem. Phys. 120 1117 DOI:10.1063/1.1627325 [Cited within:1]
20 Knoll A, Lyakhova K S, Horvat A, Krausch G, Sevink G J A and Zvelindovsky A V 2004 Nat. Mater. 3 886 DOI:10.1038/nmat1258 [Cited within:1]
21 Lyakhova K S, Sevink G J A, Zvelindovsky A V, Horvat A and Magerle R 2004 J. Chem. Phys. 120 1127 DOI:10.1063/1.1632475 [Cited within:1]
22 Ludwigs S, Krausch G, Magerle R, Zvelindovsky A V and Sevink G J A 2005 Macromolecules 38 1859 DOI:10.1021/ma049047l [Cited within:1]
23 Tsarkova L, Sevink G J A and Krausch G 2010 Adv. Polym. Sci. 227 33 DOI:10.1007/978-3-642-12876-9 [Cited within:1]
24 Koneripalli N, Singh N, Levicky R and Bates F S 1995 Macromolecules 28 2897 DOI:10.1021/ma00112a041 [Cited within:1]
25 Shull K R 1992 Macromolecules 25 2122 DOI:10.1021/ma00034a010 [Cited within:1]
26 Xiang H Q, Shin K, Kim T, Moon S I, McCarthy T J and Russell T P 2004 Macromolecules 37 5660 DOI:10.1021/ma049299m [Cited within:1]
27 Li W H, Wickham R A and Garbary R A 2006 Macromolecules 39 806 DOI:10.1021/ma052151y [Cited within:1]
28 Chen P and Liang H J 2007 Macromolecules 40 7329 DOI:10.1021/ma0705164 [Cited within:1]
29 He X H, Song M, Liang H J and Pan C Y 2001 J. Chem. Phys. 114 10510 DOI:10.1063/1.1372189 [Cited within:1]
30 Chen P, He X H and Liang H J 2006 J. Chem. Phys. 124 104906 DOI:10.1063/1.2178802 [Cited within:1]
31 Chen P and Liang H J 2008 Macromolecules 41 8938 DOI:10.1021/ma800443h [Cited within:1]
32 Yu B, Sun P C, Chen T H, Jin Q H, Ding D T, Li B H and Shi A C 2007 J. Chem. Phys. 126 204903 DOI:10.1063/1.2735626 [Cited within:1]
33 Yu B, Deng J H, Wang Z, Li B H and Shi A C 2015 Chin. Phys. B 24 046402 DOI:10.1088/1674-1056/24/4/046402 [Cited within:1]
34 Tang Q Y and Ma Y Q 2010 Soft Matter 6 4460 DOI:10.1039/c0sm00238k [Cited within:1]
35 Trombly D M, Pryamitsyn V and Ganesan V 2011 J. Chem. Phys. 134 154903 DOI:10.1063/1.3575182 [Cited within:1]
36 Mansky P and Russell T 1997 Macromolecules 30 6810 DOI:10.1021/ma970675v [Cited within:1]
37 Suh H S, Kang H M, Nealey P F and Char K 2010 Macromolucules 43 4744 DOI:10.1021/ma100150j [Cited within:1]
38 Smith A P, Sehgal A, Douglas K F, Karim A and Amis E J 2003 Macromol. Rapid Commun. 24 131 DOI:10.1002/marc.200390001 [Cited within:1]
39 Huang E, Russell T P, Harrison C and Chaikin P M 1998 Macromolecules 31 7641 DOI:10.1021/ma980705+ [Cited within:1]
40 Potemkin I I 2004 Macromolecules 37 3505 DOI:10.1021/ma035094m [Cited within:1]
41 Huang E, Pruzinsky S, Russell T P, Mays J and Hawker C J 1999 Macromolecules 32 5299 DOI:10.1021/ma990483v [Cited within:1]
42 Milner S T 1991 Science 251 905 DOI:10.1126/science.251.4996.905 [Cited within:1]
43 Ferreira P G and Leibler L 1996 J. Chem. Phys. 105 9362 DOI:10.1063/1.472725 [Cited within:1]
44 Matsen M W and Griffiths G H 2009 Eur. Phys. J. E 29 219 DOI:10.1140/epje/i2009-10470-2 [Cited within:1]
45 Dong H, Marko J F and Witten T A 1994 Macromolecules 27 6428 DOI:10.1021/ma00100a028 [Cited within:1]
46 Marko J F and Witten T A 1992 Macromolecules 25 296 DOI:10.1021/ma00027a048 [Cited within:1]
47 Zhulina E and Balazs A C 1996 Macromolecules 29 2667 DOI:10.1021/ma951396f [Cited within:1]
48 Lai P Y 1994 J. Chem. Phys. 100 3351 DOI:10.1063/1.466427 [Cited within:1]
49 Seifpour A, Spicer P, Nair N and Jayaraman A 2010 J. Chem. Phys. 132 164901 DOI:10.1063/1.3385469 [Cited within:1]
50 Xie S J, Qian H J and Lu Z Y 2015 Polymer 56 545 DOI:10.1016/j.polymer.2014.11.049 [Cited within:1]
51 Ren C L, Chen K and Ma Y Q 2005 J. Chem. Phys. 122 154904 DOI:10.1063/1.1881012 [Cited within:1]
52 Ren C L and Ma Y Q 2006 J. Am. Chem. Soc. 128 2733 DOI:10.1021/ja057569q [Cited within:1]
53 Li M and Zhu Y J 2008 Acta Phys. Sin. 57 7555(in Chinese) [Cited within:1]
54 Tang T T, Fan X S, Jin Y and Wang G W 2014 Polymer 55 3680 DOI:10.1016/j.polymer.2014.05.066 [Cited within:1]
55 Stasiak P and Matsen M W 2011 Eur. Phys. J. E 34 110 DOI:10.1140/epje/i2011-11110-0 [Cited within:1]
56 Matsen M W 2009 Eur. Phys. J. E 30 361 DOI:10.1140/epje/i2009-10534-3 [Cited within:1]
57 Li S B, Chen P, Zhang L X and Liang H J 2011 Langmuir 27 5081 DOI:10.1021/la200379h [Cited within:1]