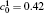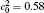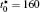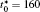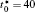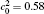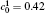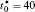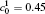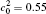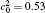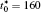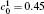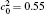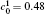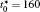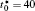Cite this Article
Li Yong-Sheng†, Wu Xing-Chao, Liu Wei, Hou Zhi-Yuan, Mei Hao-Jie. Effects of temperature gradient on the interface microstructure and diffusion of diffusion couples: Phase-field simulation. Chinese Physics B, 24(12): 126401  
Permissions
Effects of temperature gradient on the interface microstructure and diffusion of diffusion couples: Phase-field simulation
Li Yong-Sheng†, Wu Xing-Chao, Liu Wei, Hou Zhi-Yuan, Mei Hao-Jie
School of Materials Science and Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

†Corresponding author. E-mail: ysli@njust.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 51571122) and the Fundamental Research Funds for the Central Universities, China (Grant No. 30920130121012).

Abstract

The temporal interface microstructures and diffusions in the diffusion couples with the mutual interactions of the temperature gradient, concentration difference and initial aging time of the alloys are studied by phase-field simulation, and the diffusion couples are produced by the initial aged spinodal alloys with different compositions. Temporal composition evolution and volume fraction of the separated phase indicate the element diffusion direction through the interface under the temperature gradient. The increased temperature gradient induces a wide single-phase region on two sides of the interface. The uphill diffusion proceeds through the interface, no matter whether the diffusion direction is up or down with respect to the temperature gradient. For an alloy with short initial aging time, phase transformation accompanying the interdiffusion results in the straight interface with the single-phase regions on both sides. Compared with the temperature gradient, composition difference of diffusion couple and initial aging time of the alloy show greater effects on diffusion and interface microstructure.

PACS: 64.60.–i; 64.75.Nx; 66.30.Fq; 68.35.bd
Keyword: interface; diffusion; temperature gradient; phase-field
1. Introduction

The interdiffusion between the layers of the metallic multilayer can change the interface microstructure as temperature increases, which happens in the component of alloy coating, the interconnection of the packaging structure and multilayer thin film.[1– 4] From surface to inner, the temperature gradient arises from the temperature difference of layers, the element interdiffusion through the interface and the interface microstructure will be changed thereby. As a result, the mechanical and physical properties of the multilayer metal are affected. Numerous studies have been performed on the interface reaction and interdiffusion layers metals, [5– 11] in which the diffusion couple is widely used as the model to study the interdiffusion and microstructure of multilayer metal.

The diffusion path and microstructure evolution in the isothermal and stress-free multilayer diffusion couples formed by the model ternary alloy with miscibility gap have been studied by Pan et al.[12] by using the phase-field simulation. Sohn and Dayananda[13] studied the double-serpentine diffusion path in annealed Fe– Ni– Al alloys, the average values of ternary interdiffusion coefficients were determined and employed to model the concentration profiles. As an important factor, the temperature gradient[14– 18] has been studied in the bulk solid system for the diffusion and microstructure evolution. Hofman et al.[14] calculated the constituent redistribution driven by the temperature gradient based on a thermal diffusion mechanism model. Hu and Henager Jr[15] investigated the void diffusion under an applied temperature gradient field by using the Cahn-Hilliard diffusion equation, and they demonstrated that the voids migrate up the temperature gradient. Mohanty et al.[16] devised a diffuse interface model to simulate the effects of temperature gradient on the composition and microstructure of stress free binary alloy, and their heat transport model indicates that both atomic mobility and heat transport affect the magnitude and direction of flux. Snyder et al.[17] simulated the Ostwald ripening under the temperature gradient by using the steady-state diffusion equation; they found that the volume fraction of particles decreases in high temperature regions, increases in low temperature regions, and the coarsening kinetics is also affected by the temperature gradient. Ta et al.[18] studied the effect of temperature gradient on the microstructure evolution in various Ni– Al– Cr bond coat/substrate systems with thermodynamic and atomic mobilities; the phase-field simulation showed that the temperature gradient promotes the diffusions of both Al and Cr, which greatly accelerates the failures of various bond coat/substrate systems.

As concluded in the previous studies, the temperature gradient has great effects on the diffusion and microstructure, it is theoretically important to investigate the effects of temperature gradient on the interdiffusion and interface microstructure of multilayer metal. However, due to the experimental complexity in studying the temperature gradients in multilayer metals with thickness values ranging from nano- to micro-scale, the effects of temperature gradient on the diffusion and microstructure of layer metals are less investigated.

Therefore, this paper focuses on the effects of temperature gradient on the interface microstructure and diffusion through the interface of the diffusion couple, and the mutual interactions of composition difference and initial aging time (IAT) of the alloy in the diffusion couple are discussed with the temperature gradient. The phase-field simulation[11, 12, 15, 16, 18– 22] as a favorable method is adopted to study the interdiffusion and interface microstructure of diffusion couples under the temperature gradient. The linear temperature gradient is applied to the diffusion couples formed by the aged alloys with different initial aging times and different compositions including B-enriched α 1 and A-enriched α phases in the spinodal alloy, and the element diffusion direction and interface microstructure will be investigated under the temperature gradient by the phase-field simulation.

2. Model and methods

The microstructure evolution in the diffusion couples can be described by the composition field c as a function of position r and time t, and the temporal composition is controlled by the Cahn-Hilliard equation[23]

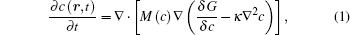
where M(c) is the chemical mobility, G is the molar Gibbs energy, and κ is the gradient energy coefficient.

The chemical mobility M(c) is given by the Darken equation[24]

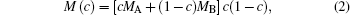
where MA and MB are the atomic mobilities of components A and B, respectively. They are related to the diffusivity by the Einstein relation Mi = Di/RT, where i denotes the component A or B of the alloy, R is the gas constant, T is the absolute temperature, Di is the diffusion coefficient, DA is assumed to be small and DB to be large: they are expressed as

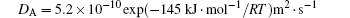
and

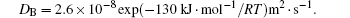
The molar Gibbs energy is expressed as

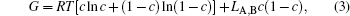
where LA, B is a regular solution parameter describing the interactions between components A and B and chosen to be 9.5  kJ· mol− 1.

The linear temperature gradient is introduced into the system with temperature increment Δ T along the horizontal direction, and the temperature T at position xi is given by T = T0 + xiΔ T, where T0 is the initial temperature in the center of the simulation cell, Δ T is the temperature increment per grid length Δ x = 0.1  μ m, the length scale is chosen such that a reasonable temperature gradient distribution and the diffusion interface are ensured.[25] The temperature gradient is activated through the temperature related free energy and the diffusion coefficient in the phase-field simulation.

In order to solve Eq.  (1) numerically, the following dimensionless parameters are used: r* = r/l, t* = tD/l2, M* = RTcM(c)/D, κ * = κ /RTcl2, G* = G/RTc, where D = 10− 23  m2· s− 1 is a normalization factor of the diffusion coefficient and l is the length scale, and Tc = 650  K is the critical temperature of phase decomposition of the alloy. Then the kinetic evolution equation Eq.  (1) is written as

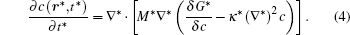
The dimensionless simulation cell is chosen to be 512Δ x* × 64Δ y* . A thermal fluctuation [− 0.005, 0.005] is added to the initial composition to trigger the phase transformation, and the gradient coefficient is chosen to be κ * = 0.5. Equation  (4) is solved by using the semi-implicit Fourier spectrum method[26] with time step Δ t* = 0.02. The lattice mismatch is chosen to be a very small value in the alloy, so the elastic strain is ignored in the present simulation.

3. Results and discussion

The calculation is performed with the periodic boundary condition in a symmetric diffusion couple, where the temperature increases from the centre (T0) to the boundary by Δ T along the horizontal direction in the simulation cell, as signalled by the arrows in Fig.  1. Therefore, we can study one of the diffusion couples with x* = 1 ∼ 256. 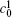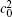The diffusion couple is formed by the two alloys aged for time with initial average compositions and of the component B on each side of the diffusion couples, as shown in Fig.  1. Then the diffusion couples are annealed for time t* . In the simulated figures, the red and blue regions represent the B-enriched α 1 phase and A-enriched α phase, respectively as signalled by the arrows in Fig.  1(c). The color bars indicate the composition value.

Fig.  1. Microstructure evolutions of diffusion couples with initial compositions 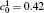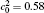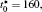and under the temperature gradient Δ T = 0.3  K/μ m for T0 = 470  K and (a) t* = 0, (b) t* = 160, (c) t* = 480.
3.1. Interface microstructure and diffusion under temperature gradient

The microstructure evolutions of diffusion couples with initial composition and (atom fraction of element B) are presented in Fig.  1, where the diffusion couple is annealed for t* = 480 under the temperature gradient Δ T = 0.3  K/μ m for T0 = 470  K, the initial aging time of the alloys is .

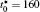
Figure  1(a) shows the initial microstructure of the diffusion couple at t* = 0 with the distinct interface. As the annealing progresses, the separated α phases are dissolved at the high temperature regions, as shown in Fig.  1(c). At the same time, the α 1 phase merges into the α 1 matrix and the α phase merges into the α matrix on the opposite side, respectively, as signalled by the dotted circles in Figs.  1(b) and 1(c). The single-phase regions on the two sides of the interface become wider with the dissolving of separated particles near the interface, as shown in Figs.  1(b) and 1(c). In the spinodal alloy, the solute undergoes the uphill diffusion driven by the chemical potential, and the solute B on the side 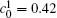diffuses to the side with the α 1 matrix, resulting in the merged matrix of α 1 and α in the interface region.

When the temperature gradient is introduced, the element diffusion through the interface will change the microstructure more obviously. The interface microstructures of diffusion couples annealed for t* = 600 with temperature gradients Δ T = 0.0, 0.2, and 0.3  K/μ m are shown in Figs.  2(a)– 2(c), respectively. The initial compositions and aging times of the diffusion couples in Fig.  2 are the same as those of Fig.  1. 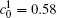As the temperature gradient increases, the fast diffusion results in the dissolution of the α 1 phase near the interface on the side , such as the α 1 phase particles signalled with the arrows in Fig.  2. The α phase particles near the interface are shrunk or dissolved on the side . As a result, the single-phase regions beside the interface become wider. Simultaneously, the α phases are dissolved in the high temperature regions for the large temperature gradient Δ T = 0.3  K/μ m, as shown in Fig.  2(c).

Fig.  2. Microstructure of diffusion couples for alloys with initial compositions and annealed for t* = 600 under the temperature gradient Δ T = 0.0 (a), 0.2 (b) and 0.3 (c) [in unit K/μ m], T0 = 470  K, .

As a phase transformation driven by thermodynamic, the B-enriched α 1 and A-enriched α coexist in the diffusion couples, the element diffusion through the interface and the dissolution of the initial separated phases are both related to the thermodynamic phase equilibrium. Owing to the temperature change continuously in the diffusion couple, the equilibrium composition of the α 1 phase decreases and α increases as temperature increases, it is just like the Soret effect[16] that induces the composition gradient in the diffusion couples, then the kinetic diffusion is affected by the composition gradient. Therefore, the concentrations of elements A and B on two sides of the diffusion couples can be changed by the diffusion, which will be discussed by the quantitative concentration variation in the following section.

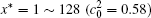
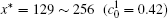
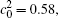
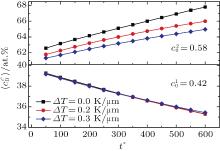The temporal average compositions of element B on two sides and of the diffusion couples are plotted in Fig.  3. For different temperature gradients, the average compositions increase on the side with high concentration and they decrease on the side with low concentration . It can be concluded that the element B diffuses from the low concentration side to the high concentration side, i.e., the uphill diffusion through the interface. Also, we can know from the composition conservation that the diffusion direction of element A is inverse to that of element B.

Fig.  3. Temporal average composition 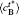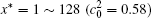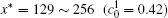on two sides and of diffusion couples shown in Fig.  2.

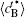
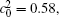
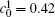
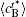
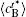
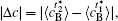
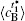
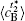
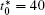
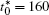
In addition, the values of are small for the large Δ T on the side while they are almost the same on the side for Δ T = 0.0, 0.2, and 0.3  K/μ m. As the thermal transport is ignored in the model, the decrease of for a large Δ T at high temperature is caused by the changed equilibrium composition of the alloy, i.e., the higher the temperature, the lower the equilibrium composition of the α 1 phase is. The difference in between before and after annealing is calculated by where and are the average compositions of component B at t* = 0 and t* = 600, respectively. The average composition difference | Δ c| for different temperature gradients and IATs are listed in Table  1. It is shown that the | Δ c| is larger for than that for for different temperature gradients, therefore, the interdiffusion of elements through the interface of the diffusion couple is intensified for a short IAT. The variation of | Δ c| also indicates that the great Δ T weakens the diffusion of element B to the high temperature regions.

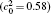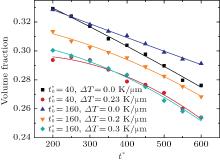
Table 1. Average concentration difference | Δ c| (at.%) on the left side and right side of the diffusion couples annealing for t* = 600 shown in Fig.  3 and Fig.  6.

The variations of B-enriched α 1 phase volume fractions in the region 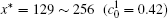and y* = 1 ∼ 64 in Fig.  2 are plotted as a function of time, and the volume fractions for Δ T = 0.0  K/μ m, and 0.23  K/μ m are also given together, as shown in Fig.  4. The volume fractions decrease as annealing progresses, the larger the temperature gradient, the smaller the volume fraction is for the same annealing time. The decrease of volume fractions in the high temperature region was also demonstrated in the temperature gradient system studied by Snyder et al.[17]

Fig.  4. Variations of volume fraction with time of B-enriched α 1 phase in the diffusion couples with x* = 129 ∼ 256 and y* = 1 ∼ 64 for different initial aging times and temperature gradients shown in Figs.  2 and 5.

The reduced volume fraction is caused by two reasons in the temperature gradient diffusion couples. First, the increased temperature reduces the supercooling, i.e., the driving force of the phase separation decreases at high temperature, as a result, the phase separation is retarded or the separated phases are dissolved again by annealing. 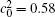Second, the decrease of volume fractions is due to the fact that the element B migrates from the low concentration side to the high concentration side during annealing, the variation of volume fraction is consistent with the decrease of composition (Fig.  3) and the recession of the α 1 phase near the interface (Fig.  2).

3.2. Interface diffusion and microstructure for a short initial aging time

In Fig.  4, the volume fractions for a short IAT and Δ T = 0.23  K/μ m have similar values to those for and Δ T = 0.3  K/μ m as indicated by the circle and diamond in Fig.  4. The variations of volume fractions also demonstrate that the short IAT can induce the strong interdiffusion in the diffusion couples. For the short IAT, the phase separation still progresses during annealing, there are more atoms randomly distributed rather than clustered, which favor the long range diffusion of atoms across the interface of the diffusion couple. As discussed in Subsection  3.1, the temperature gradient can induce the composition difference: a lower concentration of B-enriched α 1 and a higher concentration of A-enriched α at higher temperature. The concentration difference in the diffusion couples promotes the element diffusion.

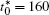
The morphology evolutions for IAT are shown in Fig.  5 with different Δ Ts. In the figure, the increased temperature reduces the B element concentration on the side inversely, the uphill diffusion supports the B element diffusion to the side . Therefore, the diffusion direction of the B element is determined by the mutual interactions between temperature gradient and initial composition difference.

Fig.  5. Microstructures of diffusion couples for alloys with initial compositions and , annealed for t* = 600 under the temperature gradient Δ T = 0.0 (a), 0.2 (b), and 0.23 (c) [in unit K/μ m]. T0 = 470  K, .

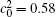
Besides the change of volume fraction with IAT, the straight interface of the diffusion couples is clearly present for the short IAT 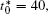as shown in Fig.  5. For a short IAT, there is no stable separated phase or is only small size particles. As the element diffuses through the interface, the solute concentration decreases near the interface, there is not enough driving force for the phase separation nor particle growth during annealing, so the same phase merging cannot happen, which leads to the single-phase region and the straight interface in the diffusion couple.

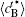
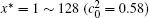
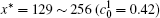
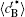
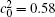
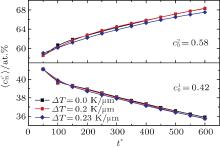Figure  6 shows the plots of the temporal average composition on the two sides and of the diffusion couples indicated in Fig.  5. The variations of on both sides of the diffusion couple are similar to those of Fig.  3. While the decrease of | Δ c| is not obvious compared with that of Fig.  3 as the Δ T increases on the side .

Fig.  6. Plots of temporal average composition 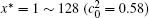versus time on two sides and of diffusion couples shown in Fig.  5.

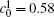
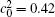
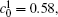
Figures  7(a) and 7(b) show the diffusion couples with and under the temperature gradient Δ T = 0.0  K/μ m and 0.4  K/μ m for T0 = 470  K, respectively, the initial aging time is and the annealing time is t* = 600. Here the temperature also increases from the center to the boundary along the horizontal direction, while the initial compositions on the two sides of the diffusion couple are inverse with respect to that of Fig.  5. It can be seen that the interface is also straight for the short IAT, and the single-phases α and α 1 are present on the sides with and , respectively.

Fig.  7. Microstructures of diffusion couples for alloys with initial compositions 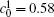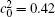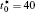and annealed for t* = 600 under the temperature gradient Δ T = 0.1  K/μ m (a) and Δ T = 0.4  K/μ m (b), T0 = 470  K, .

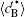
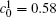
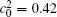
Figure  8 shows the variations of temporal average composition with time in the diffusion couple shown in Fig.  7. The still increases on the side with high concentration and decreases on the side with low concentration for Δ T = 0.0  K/μ m and Δ T = 0.4  K/μ m, which means that the element B diffuses from the low concentration to high concentration even if the diffusion direction is inverse with respect to the direction of temperature increment. Therefore, the diffusion direction of elements in the diffusion couples formed by the spinodal alloy is dominated by the initial composition, the uphill diffusion progresses through the interface no matter whether the diffusion direction is up or down with respect to the direction of temperature gradient.

Fig.  8. Variations of temporal average composition 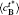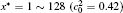with time on two sides and of diffusion couples shown in Fig.  7.
3.3. Interface diffusion and microstructure for different initial compositions

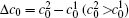
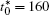
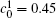
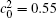
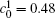
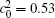
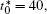
As the initial composition difference decreases, the α phase and α 1 phase are connected with themselves at the interface for the long IAT , as shown in Figs.  9(a) and 9(c), where the initial compositions of diffusion couples are and (Fig.  9(a)), and (Fig.  9(c)), the temperature gradient is Δ T = 0.4  K/μ m. However, the single-phase regions can still occur beside the interface for the short IAT as shown in Figs.  9(b) and 9(d), which have the same initial compositions as those of Figs.  9(a) and 9(c), respectively. It can be concluded from the above results that the initial composition difference Δ c0 and IAT of the alloy in the diffusion couple have a dominant influence on the interface microstructure compared with the temperature gradient.

Fig.  9. Microstructures of diffusion couples with initial compositions and in panels  (a) and (b), and in panels  (c) and (d) annealed for t* = 600 under the temperature gradient Δ T = 0.4  K/μ m, T0 = 470  K. ((a) and (c)) and 40 ((b) and (d)).

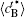
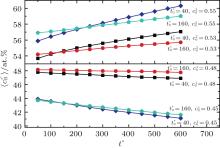Figure  10 shows the plots of the temporal average composition in the regions x* = 1 ∼ 128 and x* = 129 ∼ 256 of Figs.  9(a)– 9(d). It can be seen that the average compositions increase on the high concentration side and decrease on the low concentration side, the | Δ c| for is larger than that for (Table  2). As the initial composition difference Δ c0 decreases from 0.16 to 0.1 to 0.05, the composition difference | Δ c| decreases on both sides of the diffusion couple after annealing, which can be seen from Tables  1 and 2. It can be deduced from the composition variation that the interdiffusion is reduced as the Δ c0 decreases, which is due to the decrease of driving force of diffusion coming from the composition gradient.

Fig.  10. Variations of average composition 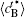with time on the two sides x* = 1 ∼ 128 and x* = 129 ∼ 256 of diffusion couples shown in Fig.  9.
Table 2. Average concentration difference | Δ c| (at.%) values on the two sides of the diffusion couples annealed for t* = 600 shown in Fig.  10.

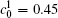
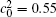
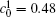
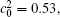
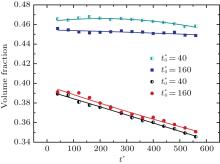Figure  11 shows the variations of volume fractions of B-enriched α 1 phase in regions with x* = 129 ∼ 256 and y* = 1 ∼ 64 of Fig.  9. The volume fractions decrease from about 0.39 to 0.35 in the diffusion couple with and as indicated by the lines signalled with a circle, while the volume fractions have almost no change in the diffusion couple with and see the lines signalled with a square. The variations of volume fraction demonstrate again that the smaller Δ c0 results in a weaker interdiffusion under temperature gradient.

Fig.  11. Variations of volume fraction with time of B-enriched α 1 phase in the diffusion couples with x* = 129 ∼ 256 and y* = 1 ∼ 64 of Fig.  9. The lines with a circle and a square represent the diffusion couple with initial compositions 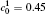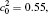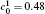and and respectively.

The simulation results give an understanding of the interface microstructure and diffusion in the diffusion couple under the effects of temperature gradient, initial composition difference and different initial aging times. As the thermodynamic driving force of phase transformation, the chemical free energy changes with temperature, thus the composition and microstructure will be changed in the temperature gradient system. In addition, the uphill diffusion dominates the diffusion direction through the interface no matter what the direction of the temperature gradient is. Therefore, the interface diffusion and microstructure in the spinodal alloy system show some differences from heat transport and mobility controlled diffusion, [16] which is of theoretical significance for understanding the interface diffusion in the diffusion couple formed by spinodal alloy.

4. Summary and conclusions

The effects of temperature gradient on the diffusion and interface microstructure of diffusion couple are studied in the binary spinodal alloy. The mobility as a function of temperature and temporal composition is incorporated into the Cahn-Hilliard equation. The thermodynamic and dynamic parameters are adopted to simulate the phase transformation. By calculating the time-dependent composition of the element and the volume fraction of the separated phase in the diffusion couple, the diffusion direction of the element through the interface is clarified under the temperature gradient. The evolution of the interface microstructure is displayed by the simulated morphology. At the same time, the effects of the initial aging time and the composition difference of the alloy on the diffusion and microstructure are also studied with the temperature gradient.

The simulation results show that the interface microstructure, straight interface with single-phase or interconnected interface, are affected mainly by the initial aging time of the alloy under the temperature gradient, the element diffusion through the interface depends on the initial composition difference between two sides of the diffusion couple. The widths of single-phase regions on both sides of the interface are enlarged as the temperature gradient increases, and the straight interface with a single-phase is present for the short initial aging time under the temperature gradient. The solute element diffuses from the low concentration to high concentration through the interface of the diffusion couple formed by the spinodal alloy, no matter whether the diffusion direction is up or down to the temperature gradient.

Reference
1 Nesbitt J A and Heckel R W 1987 Metall. Trans. A 18 2061 DOI:10.1007/BF02647078 [Cited within:1]
2 Yang D, Wu B Y, Chan Y C and Tu K N 2007 J. Appl. Phys. 102 043502 DOI:10.1063/1.2769270 [Cited within:1]
3 Kobayashi S, Tsukamoto Y, Takasugi T, Chinen T, Omori T, Ishida K and Zaefferer S 2009 Intermetallics 17 1085 DOI:10.1016/j.intermet.2009.05.009 [Cited within:1]
4 Oberhauser S, Strobl Ch, Schreiber G, Wuestefeld Ch and Rafaja D 2010 Surf. Coat. Technol. 204 2307 DOI:10.1016/j.surfcoat.2009.12.027 [Cited within:1]
5 Li Y S, Cheng X L, Xu F and Du Y L 2011 Chin. Phys. Lett. 28 106601 DOI:10.1088/0256-307X/28/10/106601 [Cited within:1]
6 Morral J E 2012 Metall. Mater. Trans. A 43 3462 DOI:10.1007/s11661-011-1026-z [Cited within:1]
7 Garimella N, Ode M, Ikeda M, Murakami H and Sohn Y H 2009 J. Phase. Equilib. Diff. 30 246 DOI:10.1007/s11669-009-9499-9 [Cited within:1]
8 Jezierska E, López G A and Zieba P 2003 Mater. Chem. Phys. 81 569 DOI:10.1016/S025-0584(03)00077-4 [Cited within:1]
9 Li Y S, Zhang L, Zhu H and Pang Y X 2013 Metall. Mater. Trans. A 44 3060 DOI:10.1007/s11661-013-1676-0 [Cited within:1]
10 Witanachchi S, Weerasingha H, Mourad H A and Mukherjee P 2010 Physica B 405 208 DOI:10.1016/j.physb.2009.08.059 [Cited within:1]
11 Heulens J, Blanpain B and Moelans N 2011 Acta Mater. 59 3946 DOI:10.1016/j.actamat.2011.03.020 [Cited within:2]
12 Pan X, Zhou N, Morral J E and Wang Y 2010 Acta Mater. 58 4149 DOI:10.1016/j.actamat.2010.04.006 [Cited within:2]
13 Sohn Y H and Dayanand a M A 2000 Acta Mater. 48 1427 DOI:10.1016/S1359-6454(99)00454-1 [Cited within:1]
14 Hofman G L, Hayes S L and Petri M C 1996 J. Nucl. Mater. 227 277 DOI:10.1016/0022-3115(95)00129-8 [Cited within:2]
15 Hu S Y and Henager C H Jr 2010 Acta Mater. 58 3230 DOI:10.1016/j.actamat.2010.01.043 [Cited within:2]
16 Mohanty R R, Guyer J E and Sohn Y H 2009 J. Appl. Phys. 106 034912 DOI:10.1063/1.3190607 [Cited within:4]
17 Snyder A, Akaiwa N, Alkemper J and Voorhees P W 1999 Metal. Mater. Trans. A 30 2341 DOI:10.1007/s11661-999-0243-1 [Cited within:2]
18 Ta N, Zhang L, Tang Y, Chen W and Du Y 2015 Surf. Coat. Technol. 261 364 DOI:10.1016/j.surfcoat.2014.10.061 [Cited within:3]
19 Ravash H, Vleugels J and Moelans N 2014 J. Mater. Sci. 49 7066 DOI:10.1007/s10853-014-8411-0 [Cited within:1]
20 Chen L Q 2002 Ann. Rev. Mater. Res. 32 113 DOI:10.1146/annurev.matsci.32.112001.132041 [Cited within:1]
21 Yang T, Zhang J, Long J, Long Q H and Chen Z 2014 Chin. Phys. B 23 088109 DOI:10.1088/1674-1056/23/8/088109 [Cited within:1]
22 Zhang L, Steinbach I and Du Y 2011 Int. J. Mater. Res. 102 371 DOI:10.3139/146.110493 [Cited within:1]
23 Cahn J W 1961 Acta Metall. 9 795 DOI:10.1016/0001-6160(61)90182-1 [Cited within:1]
24 Darken L S 1948 Trans. AIME 175 184 [Cited within:1]
25 Wu K, Chang Y A and Wang Y 2004 Scr. Mater. 50 1145 DOI:10.1016/j.scriptamat.2004.01.025 [Cited within:1]
26 Chen L Q and Shen J 1998 Comput. Phys. Commun. 108 147 DOI:10.1016/S0010-4655(97)00115-X [Cited within:1]