The study of multiferroicity is one of the hot frontiers in condensed matter physics. Multiferroic compounds allow the mutual manipulation between magnetism, electricity and strain, and hence are potential materials for next-generation mass-storage and multi-functional devices.^[1] Basically most of multiferroic materials can be divided into two categories: one with intrinsic multiferroicity and the other one with improper multiferroicity.^[2] Ferroelectricity in the materials with improper multiferroicity can be induced by the orders other than charges. For instance, it has been reported to be originated from spin ordering in TbMnO₃, ^[3] MnWO₄, ^[4] and Ni₃V₂O₈.^[5] The coupling between magnetism and electricity provides the possibility of the mutual control between the two degrees of freedom. FeVO₄ is such a compound with improper multiferroicity. Two antiferromagnetic (AF) transitions at 22  K and 15.6  K, respectively, were observed in poly-crystal FeVO₄^{[6, 7]} and further confirmed in single crystals.^[8] Neutron scattering experiments indicate that a collinear and incommensurate AF order occurs below 22  K while it becomes a non-collinear and incommensurate AF order below 15  K.^[9] Ferroelectric polarization was measured in both poly-crystal^{[9– 11]} and thin-film^{[12, 13]} samples after the second AF transition. In addition, nuclear magnetic resonance (NMR) obtained a Weiss temperature of ∼ 116 K, indicating a strong spin frustration.^[14] The experiments suggest that a magnetoelectric coupling exists in FeVO₄.

As one of the fundamental techniques in condensed matter physics, Raman scattering has been widely applied and played a unique role in the studies of multiferroic materials. Raman scattering can be used to probe the lattice distortion which is tightly correlated with ferroelectricity.^{[12, 15]} And it is also very sensitive to the magnetoelastic effect and magneto-ferroelectricity.^{[16, 17]} Doping dependence of magnetoelectric coupling can be characterized by Raman scattering, since it can sensitively catch the information on structural changes. Moreover, as a contactless and non-destructive technique, Raman scattering is particularly useful to the studies of thin films, which are hard to be measured by conventional x-ray diffraction.

In this paper, we have carried out careful Raman scattering measurements on FeVO₄ single crystals at low and high temperatures. More than 47 Raman-active modes are observed due to the low crystal symmetry. And we further made a comprehensive assignment of the observed modes by combining with first-principles calculations and symmetry analysis. The results are the first step towards the understanding of the mechanism of magnetoelectric coupling in FeVO₄.

FeVO₄ single crystals were grown by the flux growth method which has been described elsewhere.^[8] Confocal microscopic Raman scattering measurements were carried out with a Jobin Yvon T64000, equipped with liquid-nitrogen-cooled back-illuminated (deep-depletion) charge-coupled device (CCD). A 532-nm diode-pumped solid-state laser (Torus 532, Laser Quantum) was adopted as excitation source. The single crystal used in our measurement is a needle-like sample. The long side along crystalline a axis was defined as x direction. The crystal face (0, − 1, − 1) is perpendicular to z direction and y direction is determined by the right-hand screw rule. The configuration of backscattering was used and the laser beam was focused on the crystal surface with a spot of 5  μ m² ∼ 10  μ m². The laser power was fixed below 1  mW to avoid overheating.

To determine the zone-center phonon modes of FeVO₄, first-principles calculations were carried out within the framework of density functional perturbation theory (DFPT)^[20] as implemented in the Quantum-Espresso package.^[21] The ultrasoft pseudopotentials^[22] were used to describe the ion-electron interactions. For the exchange-correlation potential, the generalized gradient approximation (GGA) of Perdew– Burke– Ernzerhof^[23] was adopted. After convergence test, the kinetic energy cutoffs of the wave function and the charge density were chosen to be 40  Ry and 400  Ry, respectively. The nonmagnetic electronic structure calculations were performed with a supercell containing 6 Fe atoms, 6 V atoms, and 24 O atoms. For the Brillouin zone sampling, a 2 × 2 × 2 k-point mesh was employed. The Gaussian smearing was used around the Fermi surface. In structure optimization, both cell parameters and internal atomic positions were allowed to relax until the forces were smaller than 0.01  eV/Å . Once the equilibrium structure was obtained, the phonon frequencies and displacement patterns were calculated from the dynamic matrix.

The crystal structure of FeVO₄ is illustrated in Fig.  1. FeVO₄ has a space group of P-1 and all the atoms in its primitive cell occupy 2i positions. Three nonequivalent Fe atoms form two octahedrons of FeO₆ and one polyhedron of FeO₅. Similarly, three vandium atoms are nonequivalent and form three tetrahedrons of VO₄. The polyhedrons are bridged by oxygen atoms located at the vertexes. The point group belongs to C_i and each atom also occupies its space-inversion position. Thus, there are 36 atoms in the primitive cell. In principle this gives 108 vibration modes, among which 54 optical modes are Raman-active A_g modes and 51 optical modes are infrared A_1u modes. Such a large amount of Raman-active modes are the natural consequence of the low crystal symmetry.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Crystal structure of FeVO4. The structure consists of many polyhedrons of FeO6, FeO5, and VO4 which are connected by sharing the borders and vertexes.

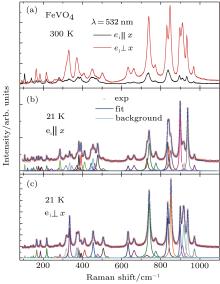
Raman spectra collected at room temperature is shown in Fig.  2(a). The phonon frequency ranges from 90  cm^{− 1} to 1000  cm^{− 1}. The polarization of incident light is parallel and perpendicular to the long side of the crystal (a axis). The polarized spectra show a strong anisotropy. The intensities under the parallel configuration are one order of magnitude smaller than those under the perpendicular configuration. This is associated with the orientation of the distorted polyhedron chain, which is almost orthogonal to a axis, indicating a quasi-one dimensional structure. It should be noted that the 104  cm^{− 1} and 139  cm^{− 1} modes appear only under the parallel configuration. This may be related to their special vibration patterns (see below).

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Raman spectra collected at different temperatures and configurations. (a) Raman spectra at room temperatures under different configurations. (b) and(c) Raman spectra at low temperatures and the corresponding Lorentzian fitting.

The crowd modes at room temperature make it quite hard to distinguish the modes from each other. Thus we further made low-temperature measurements. The low-temperature spectra exhibit a better resolution and allow us to make Lorentzian fitting (Figs.  2(b) and 2(c)). It seems that the fitting works quite well for the low-temperature spectra. 43 and 42 modes are obtained under the parallel and perpendicular configurations, respectively. By comparison of the two configurations, totally 47 modes are resolved in Raman channel. There are 7 Raman-active modes missing in the present spectra. This may be caused by the too low intensities or possible overlapping between so crowd modes. The low crystal symmetry greatly limits the application of symmetry analysis.

The assignment is achieved with the aid of first-principles calculations. The comparison between experimental and calculated mode frequencies is listed in Table 1. The modes in the range of 315  cm^{− 1} to 528  cm^{− 1} are too close to be reliably distinguished. The frequency difference between two neighboring modes is even smaller than the errors of calculations. They are put together in the table and further assignment of these modes requires more experiments like doping effect, especially isotope doping.

Table 1.

Table 1.

Table 1. The assignment of Raman modes in FeVO4. The modes of No.  1 to No.  18 and No.  42 to No.  54 can be assigned with first-principles calculations, while those of No.  19 to No.  41 are too dense in frequency to be unambiguously assigned at present (see text). Index Cal. freq./cm− 1 Expt. freq. (21  K)/cm− 1 Expt. freq. (300  K)/cm− 1 1 91.3 92.13 90.1 2 102.1 105.9769 103.9 3 117.9 120.3621 118.09 4 127.7 135.9075 133.9 5 141.6 139.7444 139.43 6 151.5 148.8023 148 7 161.2 166.3215 163.3 8 169.2 176.2091 173.67 9 175.3 185.3834 182.82 10 177.4 191.7949 187.7 11 193.2 217.7747 215.6 12 209.9 226.4515 223.47 13 214.7 242.1796 238.4 14 222.7 260.4192 258.46 15 250 270.2027 264.88 16 261.2 277.1371 274.08 17 268.5 285.3859 281.28 18 278.8 296.434 294.45 19 296.4 315.6902 311.17 20 304.9 317.7283 314.43 21 311.2 323.6721 317.73 22 323.3 334.486 330.23 23 324.5 345.5894 344 24 335.4 369.9281 367.7 25 338.8 377.098 370.66 26 355.7 382.0173 377 27 364.9 392.7664 390 28 370.3 410.9871 407 29 378 443.0673 434.5 30 392.6 454.7996 449.08 31 404.2 463.9439 457.8 32 412.7 478.0178 471.7 33 421.7 506.2249 501.18 34 430.5 528.784 – 35 445.2 36 454.4 37 460.1 38 486.0 39 495.8 40 504.7 41 535.3 42 583.1 633.1113 632.5 43 602.8 663.7241 661.67 44 620.3 728.5267 728 45 675.9 740.6417 738.19 46 726.4 774.1781 771.32 47 741.5 835.2827 830.37 48 750.2 841.5083 837.57 49 844.8 851.9171 847.53 50 849.1 899.3122 894.86 51 855.3 910.4715 906.35 52 887.3 917.7792 910.7 53 909.5 937.4253 932.55 54 921 971.7895 968.36

Table 1. The assignment of Raman modes in FeVO4. The modes of No.  1 to No.  18 and No.  42 to No.  54 can be assigned with first-principles calculations, while those of No.  19 to No.  41 are too dense in frequency to be unambiguously assigned at present (see text).

Similar to the case of AlVO₄, ^[19] most of the modes in the high-frequency region come from the stretching of V– O– Fe bond. And the low-frequency modes are dominated by the relative torsion motions between the polyhedrons. The modes in the intermediate frequency region are the combination of the low-frequency and high-frequency modes. The vibration patterns of some selected low-frequency torsion modes and high-frequency stretching modes are depicted in Figs.  3(a) and 3(b), respectively. The two modes which only appear under the parallel configuration are still unclear at present and their origins needs to be further studied in experiments and theoretical calculations.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Atomic displacement patterns for selected Raman-active Ag modes of FeVO4. The index in each pattern corresponds to that listed in Table  1. 1– 8: Bending modes between rigid polyhedron. 48– 54: Stretching modes of V– O– Fe bonds.

In summary, we made Raman scattering measurements on single-crystal FeVO₄ and resolved at least 47 Raman-active modes. The spectra exhibit a strong anisotropy under two polarization configurations. The spectra can be taken as fingerprints, which are useful to the material synthesis and the studies of doping effect and thin-film samples. The mode assignment has been made by combining first-principles calculations and symmetry analysis. The results provide the fundamental information on lattice dynamics and allow to further explore the ferroelectric transition and magnetoelectric coupling in FeVO₄.