†Corresponding author. E-mail: riping@ysu.edu.cn
*Project supported by the National Basic Research Program of China (Grant No. 2013CB733000) and the National Natural Science Foundation of China (Grant Nos. 51271161 and 51271162).
Molecular dynamics simulation is used to investigate the relationship between Voronoi entropy and viscosity for rapid solidification processing of Zr36Cu64 binary alloy melt. The simulation results at different temperatures, cooling rates, and pressures, show that Voronoi entropy is able to accurately describe the relationship of the transition between the cluster structure and the viscosity of Zr36Cu64 binary alloy melt through Voronoi polyhedron analysis. That is, the higher the degree of order of the microstructure, the lower the Voronoi entropy is and the higher the viscosity is. The simulation provides an important reference for studying metallic glass with high glass-forming ability.
Metallic glass (MG) has many superior properties to those of crystalline metals, hence metallic materials properties can be significantly improved by glass transition.[1– 5] For the study of metallic glass, its atomic structure and cluster structure are still an open issue to date.[6] Therefore, many structural models for metallic glass have been suggested. For example, Bernal[7] proposed a structural model for metallic glass, which involved a dense packing of hard spheres in 1960. This model has been widely used since then. Gaskell[8] considered short-range order (SRO) as a conceptual structural unit of metallic glass, and suggested that SRO be the fundamental structural unit in metallic glass.
In recent years, ZrCu binary alloy has attracted a great deal of attention due to its promising physical and chemical properties.[9] The alloy has been considered a potential high-temperature structural material in both the aviation and nuclear industries. As a kind of ZrCu binary alloy, Zr36Cu64 metallic glass has attracted increasing attention due to its excellent properties. Because Zr36Cu64 metallic glass is produced by the rapid cooling of high-temperature melts, it retains the structural properties of the liquid metal. Viscosity, as the most typical physical property used to characterize high-temperature melts, shows the atom migration ability of the liquid metal and its variation reflects the structural variation of SRO therein.[10, 11] Therefore, the atomic structure of Zr36Cu64 metallic glass can be partly characterized by using viscosity. However, owing to the high melting point and active chemical properties of metallic glasses, the viscosity varies significantly in the super-cooled liquid region. Therefore, it is difficult to accurately measure experimentally at a certain temperature, particularly as it changes significantly in a low-temperature region. Previous experimental results indicated that viscosities are divided into two categories: one is that the viscosity versus temperature curve discontinuously changes, which is an abnormal phenomenon, and the other is that the viscosity versus temperature curve is smooth and shows an exponential trend.[12] Molecular dynamics-based computer simulation, as a new kind of tool for the study of materials atomic structure, can effectively calculate the viscosity.[13, 14] In the present work, the rapid solidification of a Zr36Cu64 alloy melt is simulated by using molecular dynamics technique and the variations of structural configurations and contents of each configuration of the original cluster are analyzed by the Voronoi polyhedron method. In addition, Voronoi entropy is introduced to characterize the degree of disorder of the microstructure and simulate the viscosity of the melt in the super-cooled liquid region, and the relationship between Voronoi entropy and viscosity on an atomic scale is revealed.
Molecular dynamics has been widely used in the study of the glass transition of Zr36Cu64 binary alloy. In this simulation, a model containing 3 × 104 atoms (1.08 × 104 Zr atoms and 1.92 × 104 Cu atoms) was established. The embedded-atom model (EAM) potential was developed for the Zr36Cu64 binary alloys to describe the interatomic interactions in a many-body framework, [15, 16] and the simulation was conducted by applying periodic boundary conditions, and an NPT system was adopted. The simulation was performed at an initial temperature of 2 × 103 K and after reaching an equilibrium liquid state upon sufficient relaxation. Subsequently, in order to form the MG, the system was cooled down from 2 × 103 K to 300 K under the cooling rate of 1012 K· s− 1. The atomic positions and other relevant data in the system were recorded in steps of 10 K in the cooling process (each time step is 1 fs). By adjusting the step size, atomic configurations at different temperatures, cooling rates, and pressures were obtained. Then based on an NVE system, the viscosity was simulated. Because of low temperature affecting the kinetic property of the amorphous alloy, we simulated viscosities by using the Green– Kubo formula at 1000 K, 1050 K, 1100 K, 1150 K, 1200 K, and 1300 K, which are all above glass translation temperature Tg. Finally, several structural characterization methods were used to indicate the SRO structural evolutions of Zr36Cu64 binary alloy.
Figure 1 shows the pair distribution function (PDF) curve and partial PDF curve of the binary alloy at 900 K. PDF describes the probability that atoms occur on the neighboring shell of the central atom. It is observed that the second peak of the gtotal(r) split quite distinctly. As is well known, the splitting of the second peak evinces the formation of metallic glass. Therefore, it indicated that an amorphous structure was generated at 900 K. Furthermore, the reliability of the simulation was verified by comparing the peak positions.[17]
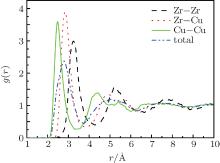 | Fig. 1. PDF curve and partial PDF curve of the Zr36Cu64 alloy melt at 900 K during cooling at 0 GPa and 1012 K· s− 1. |
The structure of SRO plays an important role in the understanding of the properties of the amorphous structure. Voronoi is the smallest closed polyhedral convex polyhedron, in which the perpendicular bisecting plane of the center atom and its nearest neighbor atoms are surrounded by the connection, Voronoi polyhedra are effective in distinguishing the structure of the SRO and can provide relevant data about different atoms, including the atomic coordination number (CN), the three-dimensional distribution among the central atoms, and the distribution of all of its neighbouring atoms.[18– 23] By applying spatial relationship analysis of the Voronoi polyhedron, the order variation of the microstructure of the melts can be studied during their rapid cooling. Therefore, Voronoi entropy[24] was introduced to characterize the degree of disorder of the microstructure, and it was defined as
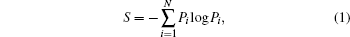
where Pi represents the fraction of Voronoi type i in a sample, and N is the total number of local structures. If there is only one single local structure, Pi is 1 and the probability of all other types of polyhedra is 0, then S = 0, which indicates that the system is in the most ordered structure configuration. However, if all the structure types have the same probability of 1/N, S will reach its maximum value, which indicates that the system is in the most disordered configuration.
The calculation of viscosity is based on the Green– Kubo formula, the method that is commonly used in the molecular dynamics simulation, which relates the ensemble average of the auto-correlation of the stress/pressure tensor to viscosity by the following equation[25]
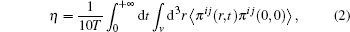
where T is the temperature, π ij, i, j = x, y, z, are components of the stress tensor, and 〈 · · · 〉 denotes the ensemble average in thermal equilibrium. This can be done in a steady-state equilibrium simulation where momentum flows continuously through the simulation box.
Figure 2 shows the variations of viscosity and Voronoi entropy with temperature during rapid cooling. It indicates that the viscosity of the melt increases exponentially with temperature decreasing. When the temperature is reduced to approximately 1100 K, the viscosity increases rapidly as the temperature decreases further. This shows that with temperature decreasing, the microstructure of the melt changes near liquidus temperature, atoms are combined into short-range order or medium-range ordered cluster compounds. The slight reduction of temperature corresponds to a sharp rise in viscosity, and the atomic rearrangement or diffusion is extremely difficult. The viscosity is several orders in magnitude lower than that of the experiment.[26, 27] Because of inherent limitations of molecular dynamics (MD) method, the time scale in MD simulation is much shorter than the experimental time scale. Notwithstanding, one should keep it in mind that the behaviors of materials can be significantly different because of cooling rates being different. The cooling rate of MD is several orders in magnitude higher than the experimental result. As is well known, the higher cooling rates will lead to higher free volume in the process of forming the metallic glass.[28] This will further affect critically the nature of the metallic glass, such as atomic structure and dynamic property.[29] However, the experimental result and the simulation result are in agreement: both show that the viscosity of the melt increases exponentially with temperature decreasing.
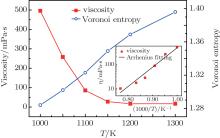 | Fig. 2. Viscosity and Voronoi entropy versus temperature curve of the alloy metal during cooling at 0 GPa and 1012 K· s− 1. The inset shows the Arrhenius fitting. |
Figure 2 shows that the viscosity change conforms with the following Arrhenius law in high temperature liquid region

where η is the viscosity, A is a constant, E is the activation energy, and kB is the Boltzmann constant. In addition, figure 2 shows that the Voronoi entropy decreases during rapid cooling, which indicates that the structure of the alloy becomes more ordered. It is suggested that with the decrease of temperature, the type of cluster in the melt decreases, and the quantity of some clusters increases, and the stability and order of the microstructure are enhanced. Figure 3 shows the content value of each polyhedron (only those with content values exceeding 5% are marked) at different temperatures. It can be seen that the content value of icosahedral 〈 0, 0, 12, 0〉 increases continuously, while the other Voronoi polyhedron changes irregularly in the rapid solidification. The symmetric icosahedral form improves the stability and orderliness of the metallic glass even further.[30] 〈 0, 0, 12, 0〉 (full icosahedron) is found to be a key structural motif in amorphous Cu– Zr alloy, characterized by high packing density[31] and high shear resistance. In the cooling process, the more icosahedra increase the viscosity, and reduce the entropy. The aforementioned points all indicate that the structure of the melt changes at temperatures near the super-cooled liquid region. The structure of the alloy changes into a structure with a more ordered five-fold symmetry. Furthermore, with the decrease of temperature, the Voronoi entropy decreases, the SRO of the atoms is intensified, the rearrangement or diffusion of atoms becomes more difficult, and the viscosity increases significantly.
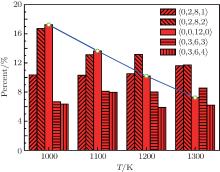 | Fig. 3. Proportions of Voronoi polyhedra at different temperatures during cooling at 0 GPa and 1012 K· s− 1. |
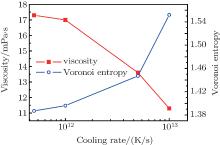
As shown in Fig. 4, with the increase of cooling rate, the viscosity of the melt decreases, while the Voronoi entropy increases. This is because the more rapid the rate of cooling, the more free volume is retained in the transition of the liquid state to an amorphous state.[32] In this condition, the atoms are more active and the degree of disorder increases. All of these can induce the Voronoi entropy to increase and the viscosity thus to decrease.
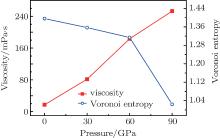
Figure 5 shows that with the increase of pressure during rapid cooling, the viscosity of the melt increases, while its Voronoi entropy decreases. As pressure increases, the melt becomes more compact because of weaker liquidity and stronger binding force between their atomic groups. Therefore, the friction opposing the movement of atoms or atomic groups and the neighboring atoms, or atomic groups, also increases. In this condition, the Voronoi entropy decreases; while the viscosity increases. This shows that the effects of cooling and increasing pressure on the viscosity of the melt have a similar effect, indicating the change of microstructure.
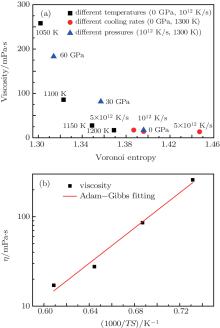
Figure 6(a) shows that with Voronoi entropy decreasing, the viscosity of the melt increases under different solidification conditions. In 1965, Adam and Gibbs (AG) proposed Adam– Gibbs relation, [33] which is often used to understand the nature of viscosity:
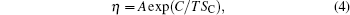
where SC is the configurational entropy and C is a constant that relates to the barrier height of atomic restructuring. Figure 6(b) proves that the viscosity and Voronoi entropy obey the Adam– Gibbs relation in the high temperature liquid region. This also suggests that Voronoi entropy has a good corresponding relationship with viscosity. The aforementioned points all indicate that the more ordered the microstructure in Zr36Cu64 alloy, the lower the Voronoi entropy is and the higher the viscosity is. With the decrease of the Voronoi entropy, the viscosity of the system increases sharply. The more ordered the local structure of the melt, the higher the viscosity is. Especially when the Voronoi entropy reaches a critical value (about 1.35), the slight increase of the degree of order causes a great change in viscosity. This proves that the effect of the microstructure on the dynamics is very obvious. Furthermore, viscosity is most sensitive to temperature, and the second effect on the viscosity is pressure. Although the effect of the cooling rate is minimum, it still has an obvious effect on the viscosity, and the sensitive degrees under different simulation conditions need further studying.
By simulating the configurations of Zr36Cu64 binary alloy melts at different temperatures and pressures, it is found that the structure of the melt changes into a five-fold symmetrical structure with a higher degree of order at temperatures near its super-cooled liquid region. In the transition, the Voronoi entropy decreases, the SRO of the atoms increases, and the viscosity is improved significantly. With increasing the rate of cooling, the viscosity of the melt in the super-cooled liquid region decreases, while Voronoi entropy increases. Moreover, with increasing pressure, the viscosity of the melt increases while the Voronoi entropy decreases. All of these facts indicate that in the rapid solidification of the high-temperature melt, the Voronoi entropy varies with viscosity. Simulation, based on molecular dynamics, provides a theoretical basis for forming the metallic glass with high glass-forming ability.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|