The negative-index material (NIM) was first theoretically proposed by Veselago^[1] in 1968. The NIM, which is proposed as a perfect lens of unlimited resolution, has attracted a great deal of attention from researchers.^[2] Metamaterials and photonic crystals (PCs) have been proposed to construct NIM in the last ten years.^{[3– 6]} However, most NIM constructions usually have a narrow operating bandwidth and the effective index is not tunable. In recent years, some researchers used magnetic materials to construct tunable NIM at microwave frequencies.^{[7– 9]} The negative index can be realized based on the ferromagnetic resonance effect and the resonance frequency can be tuned by varying the external magnetic field strength. Unfortunately, the ferromagnetic resonance effect is suppressed dramatically as the operating frequency increases from microwave frequency to optical frequency. It means that the tunable NIM, which is based on the ferromagnetic resonance effect, cannot be used at optical frequency.

On the other hand, researchers have developed many selfassembled PCs to provide a photonic response in the visible regime.^{[10, 11]} Magnetic fluid, as a kind of easy-made mature nanoscale magnetic material, has proved to be an excellent candidate for fabricating self-assembled PCs, ^{[11, 12]} especially the band-tunable PC with a fast and reversible response to external magnetic fields. In Ref.  [13], tunable negative refraction at optical frequencies was theoretically demonstrated in ferrofluids containing Fe₃O₄ nanoparticles coated by an isotropic Ag shell. The proposed tunable metamaterial can exhibit negative refraction due to the hyperbolic dispersion.^[14] Thus, it is hard to use in the imaging system because of the strong anisotropy. In addition, the Ag shell results in the loss significantly.

In this paper, the proposed work focuses on the tunability of the negative refractive index via theoretical simulations based on the experimental data in the literature. The results show that the tunable negative-index PC can be realized easily by using general colloidal magnetic fluid in the optical regime, which may be desirable for tunable near-field imaging systems.

Under an external magnetic field H, which is perpendicular to the magnetic fluid film surface, the magnetic nanoparticles are agglomerated due to the attraction among particles. The magnetic columns will appear when H is beyond a critical value, and then the fluid becomes a two-phase system (solid and liquid phases). Structural patterns will evolve from a onedimensional ordered array to a two-dimensional (2D) ordered array as H increases. Finally, a two-dimensional PC slab can be formed^{[15, 16]} as shown in Fig.  1. The self-assembled PC usually has a triangular lattice structure due to the condition of minimum total energy.^[17] Strictly speaking, it is a quasi-twodimensional PC because of the finite thickness of the sample in practice.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematic diagram of the PC slab formed in a magnetic fluid under externally perpendicular magnetic field and confined by the substrate and superstratum along the direction of the magnetic field. a and h are the periods and heights of the magnetic columns, respectively.

In this work, a set of experimental data in Refs.  [18] and [19] for typical water-based Fe₃O₄ magnetic fluid samples are referred to. In the self-assembled process of PC, the permittivity of magnetic columns is close to that in the solid state and does not vary with the increase of H. However, the permittivity of the liquid phase decreases with the increase of H due to more magnetic nanoparticles aggregating into magnetic columns. Nevertheless, it is hard to measure the index of the liquid phase directly. For calculating the band structure, the relationship is needed between the concentrations of nanoparticles in the liquid phase and H. In practice, the relationship can be derived by measuring the field-dependent magnetization M of the liquid phase, because M is dependent on the number of magnetic nanoparticles per unit volume in the liquid phase. The relationship between M and H can be measured directly. The empirical formula can be expressed as^[19]

Here, ɛ _liq is the permittivity of the liquid phase and the magnetic permeability is 1 for optical frequency. Thus, according to Eq.  (1), the field-dependent index of liquid phase n_liq can be calculated by using the experimental data in Ref.  [19].

The area ratio A_col/A is usually used to express the density of magnetic columns in practice and A_col is the area occupied by the magnetic columns with an area of A. For triangular structural patterns, the area ratio is expressed as

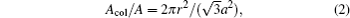
where r is the radius of the cross-section of the magnetic column and a is the perpendicular distance between the centers of adjacent magnetic columns, namely, the lattice constant. Then, according to Eq.  (2), the value of r/a can be calculated through 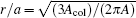by using the experimental data in Ref.  [18]. In general, according to the previous analysis, listed in Table  1 are the calculation results of fielddependent n_liq and r/a under different magnetic field strengths by using the experimental data in Refs.  [18] and [19]. In the near-infrared and visible regime, the index of the magnetic column is a constant of 2.2 for Fe₃O₄.^[20]

Table 1.

Table 1.

Table 1. The calculated results of nliq and r/a under different magnetic field strengths in the magnetic fluid film. The unit 1  Oe= 79.5775  A/m. H/Oe nliq r/a 150 1.445 0.185 175 1.442 0.200 200 1.440 0.209 225 1.438 0.213 250 1.437 0.216

Table 1. The calculated results of nliq and r/a under different magnetic field strengths in the magnetic fluid film. The unit 1  Oe= 79.5775  A/m.

The PC slab can be regarded as an ideal two-dimensional (2D) PC when the column height h is much larger than the lattice constant a (about 10 times). Figures  2(a) and 2(b) show the band structures for transverse magnetic (TM) polarization (electric field is parallel to the columns) and transverse electric (TE) polarization (magnetic field is parallel to the columns) under external magnetic field H = 250  Oe by the plane wave expansion (PWE) method. Here, the frequency is normalized as λ /a. A band gap between the first and second band is presented in TM mode, but it does not appear in the TE mode.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Band structures of the 2D PC under external magnetic field 250  Oe for (a) TM polarization and (b) TE polarization.

The refraction in PC is more complicated than that in uniform medium. In PC, an incident wave can produce multiple refracted Bloch-wave orders, if there are multiple branches of dispersion contours at the same frequency. Therefore, the candidate PC should guarantee the absence of any high-order Bragg reflections for any angle of incidence. Furthermore, the periodic modulation effect in the candidate PC should be strong enough in order to make the equal frequency surface (EFS) keep a circular shape.^[21] Figures  3(a) and 3(b) show the EFS contours for TM polarization and TE polarization at several relevant frequencies in the second band. It is clear that the EFS shape of the TM mode is closer to the isotropic case than that of TE modes. It indicates that the periodic modulation effect for TM polarization in the second band is stronger. The EFS shape of TE modes cannot keep a circular shape even near the Γ points around f = 0.6551. Therefore, the analysis of TM modes is conducted in detail. Figure  4 shows the first band gap of TM modes as a function of external magnetic field H. With H increasing, the gap width increases, but the mid-frequency of the gap decreases. The feature has also been demonstrated experimentally.^{[22, 23]} The results show that the periodic modulation strength will be weakened as H decreases.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. EFS contours of the 2D PC under external magnetic field 250  Oe for (a) TM polarization and (b) TE polarization at several relevant frequencies in the second band. The gray line shows the first Brillouin zone.

Fig.  4.

	Figure Option ViewDownloadNew Window
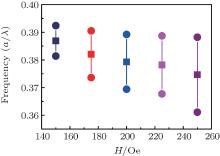	Fig.  4. The first band gap of TM modes as a function of magnetic field. Square symbols denote the middle of the band gaps and the vertical bars mark the spans of the band gaps.

From Fig.  3(a), it is clear that EFS contours shrink as frequency increases. This means that the group velocities are opposite to the phase velocities. A developing approach of effective medium theory beyond the static regime^{[24, 25]} has been employed to investigate the behavior of effective permittivity ɛ _e and permeability μ _e. Figure  5(b) shows the calculated results of ɛ _e and μ _e with H = 250  Oe for TM polarization. Both ɛ _e and μ _e exhibit a Lorentz-type anomalous dispersion. The resonant frequencies appear at values 0.389 and 0.369 of ɛ _e and μ _e respectively. The regions for ɛ _e < 0 and μ _e < 0 are located at 0.389 < f < 0.627 and 0.369 < f < 0.701, respectively. It indicates that the magnetic resonance has a larger resonance width than the electric resonance. In this work, since both ɛ _e and μ _e are a real function of f, the effective refractive index n_eff can be either real (ɛ _e > 0 and μ _e > 0 or ɛ _e < 0 and μ _e < 0) or imaginary (ɛ _e > 0 and μ _e < 0 or ɛ _e < 0 and μ _e > 0). When n_eff is real, the figure of merit (FOM), which is defined as − Re(n_eff)/Im(n_eff), ^{[26, 27]} is infinite. When n_eff is imaginary, FOM is zero. The band gap appears at the resonant frequencies as shown in Fig.  5(a). The fields are localized around individual dielectric cylinders with rather weak interactions between neighboring cells at the resonant frequencies. The localized modes were discussed in detail in Ref.  [27]. In the region of the second band, n_eff is negative due to ɛ _e < 0 and μ _e < 0 simultaneously as shown in Fig.  5(b).

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) Band structure, (b) effective permittivity ɛ e and permeability μ e of 2D PC with external magnetic field 200  Oe for TM polarization. In panel (a), the shadow area indicates the band gap.

Figure  6(a) shows the calculated effective indices n_eff as a function of magnetic field at f = 0.45 along the Γ M direction. The effective index increases from – 1 to – 0.964 as H increases from 150  Oe to 250  Oe. Figures  6(b) and 6(c) show the normalized average intensities over a period at H = 150  Oe and H = 250  Oe, respectively. A continuous wave point source with f = 0.45 is placed at a distance d₀ = 0.65λ from the lower interface of the PC lens. The width of PC lens d is 1.34λ . The images are located at distances d_{i_150  Oe} = 0.44λ and d_{i_250  Oe} = 0.49λ from the upper interface, respectively. It indicates clearly that the effective refractive index of such a PC lens can be manipulated by the external magnetic field strength. For an ideal superlens with refractive index equal to – 1, d should be equal to d₀ + d_i.^[28] The mismatch between d and d₀ + d_i is due to the anisotropy of the EFS. For example, the EFS shape of the PC lens at H = 250  Oe is not circular when 0.39 < f < 0.55 as shown in Fig.  3(a). Similarly, the full widths at half-maximum (FWHMs) of both images at H = 150  Oe (FWHM = 0.83λ ) and H = 250  Oe (FWHM = 0.63λ ) are both larger than λ /2 as shown in Fig.  6(d). The FWHM of the image at H = 250  Oe is smaller than that at H = 150  Oe due to a stronger periodic modulation effect. Fortunately, the resolution problem can be settled by fixing a subwavelength metallic grating before the PC lens. The grating can inhibit the zero-order diffraction and enhance the high-order diffraction to achieve super-resolution.^[29] Figure  6(e) shows the transmission of light from a point source with f = 0.45 through the PC lens as a function of H. It can be seen that the transmittivities are more than 0.45 for all the cases.

Fig.  6.

Figure Option ViewDownloadNew Window

Fig.  6. (a) Calculated effective indices of 2D PCs versus external magnetic field at f = 0.45 along the Γ M direction. The normalized average intensities of a point source with f = 0.45 located at 0.65λ from the PC lens at (b) H = 150  Oe and (c) H = 250  Oe. In panels  (b) and (c), the solid lines show the position of the PC lens. The z positions of the images are marked by the dashed lines. (d) The normalized average intensities along the x direction at the image plane at H = 150  Oe and H = 250  Oe. (e) The transmission of light from a point source with f = 0.45 through the PC lens as a function of external magnetic field.

When the column height h is of the same order with the lattice constant a, the band structure will be different from the ideal 2D case. The states in PC slabs are not purely TM nor TE polarized because of the absence of translational symmetry in the vertical direction (perpendicular to the plane of periodicity). Instead, the guided bands can be classified as odd or even modes. However, the odd and even modes have strong similarities to TM and TE modes, respectively, in two dimensions.^[30]

For PC slab with finite thickness, there is a light cone in the band structure, which consists of all the states existing in the bulk background. When a guided band reaches the edge of the light cone, it extends infinitely far into the background, and cannot be used to permanently confine the light within the slab. In other words, only the bands below the light cone can be guided in the PC slab. The position of the light cone depends on the refractive indices of substrate and superstratum. It should be tried to use a low refractive index material (such as aerogel glass, whose index is nearly 1) as the cladding layer. Here, the index of the cladding layer is assumed to be 1. The band structures, which lie above in the light cone, are retained here, because these modes could be important for some applications such as the photonic crystal LED.^[31] The band structures for PC slabs are calculated using both the finitedifference time-domain (FDTD) method and PWE method. Since PWE requires periodicity in all directions, the photonic crystal slab is already two-dimensionally periodic, and it can be imposed by a three-dimensional periodicity through a periodic sequence of slabs separated by a sufficient amount of background region. Because the guided modes are localized within the slab, the addition of periodic slabs at large intervals exerts little effect on their frequencies. However, this supercell approach inevitably results in spurious modes and subsequent spurious bands.

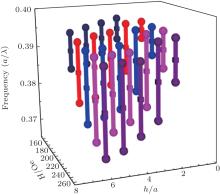
Figure  7 shows the band structure of PC slab with h = a at H = 250  Oe for odd modes as an example. The results of the FDTD method (empty circles) and PWE method (solid line) agree well with each other. It can be seen that spurious modes arise from the fake slabs of the supercell approach in the PWE method (solid line), and all the bands move to a slightly higher frequency compared with the case of the 2D PC (black dash line). Figure  8 shows the first band gap of odd modes as a function of H and h. The gap width decreases as either H or h decreases, on the contrary, the mid-frequency of the gap increases. The calculated results indicate that the decrease of h weakens the periodic modulation strength, thereby reducing the imaging quality of the PC slab lens.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Band structures of the PC slab with h = a at H = 250  Oe for odd modes using the FDTD (empty circles) and PWE methods (solid line). Gray lines specify the light line. Dashed line shows the band structure of the ideal 2D PC at H = 250  Oe for TM modes using the PWE method for comparison.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. The first band gap of odd modes as a function of H and h. Here, H changes from 150  Oe to 250  Oe and h changes from 2a to 6a. Solid symbols denote the middle of the band gaps and the vertical bars mark the spans of the band gaps.

Figures  9(a)– 9(c) show the normalized average intensities over a period at H = 150  Oe with h = 3a, H = 250  Oe with h = 3a, and H = 250  Oe with h = 4a, respectively. The calculation conditions are the same as those in Figs.  6(b) and 6(c), except that the normalized frequency of the point source is 0.44. The images are located at d_i1 = 0.144λ , d_i2 = 0.281λ , and d_i3 = 0.349λ from the upper interface in Figs.  9(b)– 9(c), respectively. The results show that the effective refractive index of the PC lens can also be manipulated by h, besides H.

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. Normalized average intensities of a point source with f = 0.44 located at 0.65λ from the PC slab lens at (a) H = 150  Oe with h = 3a, (b) H = 250  Oe with h = 3a, and (c) H = 250  Oe with h = 4a. In panels (a), (b), and (c), the solid lines show the position of the PC slab lens. The z positions of the images are marked by the dashed lines.

In this work, the model of a self-assembled PC slab lens is established by using colloidal magnetic fluids. The effective refractive index of the PC slab lens can be tuned easily by varying the external magnetic field strength. The results show that around frequency 0.45, the effective refractive index is nearly – 1 and the FWHM of the image is close to the diffraction limit. It may have great potential for tunable nearfield imaging systems. Considering the fact that the periodic modulation strength of the PC slab lens will decrease as the column height decreases, which leads to the degradation of image quality, a thick container filled with colloidal magnetic fluids should be used to form the self-assembled PC slab lens.