†Corresponding author. E-mail: zsl-dpi@mail.tsinghua.edu.cn
*Project supported by the Beijing Higher Education Young Elite Teacher Project, China (Grant No. YETP0086), the Tsinghua University Initiative Scientific Research Programme, China (Grant No. 2012Z02166), and the Special-funded Programme on National Key Scientific Instruments and Equipment Development of China (Grant No. 2011YQ04013603).
We investigate the total intensity fluctuation spectrum of the two-longitudinal- mode Nd:YVO4 microchip laser (ML). We find that low-frequency relaxation oscillation (RO) peaks still appear in the total intensity fluctuation spectrum, which is different from a previous research result that the low-frequency RO peaks exist in the spectrum of the individual mode but compensate for each other totally in the total intensity fluctuation spectrum. Taking the spatial hole-burning effect into account, one and two-mode rate equations for Nd:YVO4 ML laser are established and studied. Based on the theoretical model, we find that when the gains and losses for two longitudinal models are different, a low-frequency RO peak will appear in the total intensity fluctuation spectrum, while when they share the same gain and loss, the total spectrum will behave like that of a single mode laser. Theoretical simulation results coincide with experimental results very well.
For class B lasers, in which polarization dynamics can be adiabatically eliminated, the intensity fluctuation of the output laser has been widely investigated since McCumber predicated a noise peak corresponding to regular relaxation oscillation (RO) in the intensity spectrum.[1] Compared with single mode laser, the intensity fluctuation spectra of multimode lasers exhibit more complex behaviors.[2, 3] In the early days of experimental observations and theoretical interpretation, it was known that in multimode lasers the individual mode intensity spectrum shows low-frequency anti-phase ROs while the total output intensity spectrum only shows the regular RO peak.[2– 10] Rate equations which take the cross-saturation effect into consideration were established to explain the experimental phenomenon.[2, 6– 11] Recently, a frequency-shift self-mixing interferometer based on class B ML has attracted a great deal of academic attention due to its high sensitivity and stability.[12– 18] The intensity spectra will come into chaos if the frequency-shift signal coincides with any of the RO peaks.[19] On the other hand, the signal detuning processes in self-mixing interference are different for one-mode and multimode lasers. In order to ensure the stability and accuracy of self-mixing interference, a clean and smooth intensity fluctuation spectrum except the regular RO peak is needed. The phenomenon in a two-mode laser is representative and relatively simple compared with that in a multimode laser. So the purpose of this work is to investigate the dynamical properties of the total intensity spectrum in two-mode Nd:YVO4 ML. Based on the dynamic properties, we can distinguish whether the Nd:YVO4 laser works in one-mode or two-mode through the intensity fluctuation spectra.
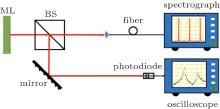
The experimental configuration is shown in Fig. 1. The thickness of the microchip Nd:YVO4 crystal is 0.78-mm and both faces of it are coated to form a resonator. Its input is coated to be highly reflective at a lasing wavelength of 1064 nm and antireflective at a pumping wavelength of 808 nm. The output surface is coated to be of 4.5% transmittance at 1064 nm. The pump light, produced by a TO18 laser diode and shaped by an aspheric lens, is focused onto the center of the Nd:YVO4 crystal. The threshold of Nd:YVO4 ML is about 60 mW while the adjustable range of the pump light is 0 mW– 300 mW. The output light of Nd:YVO4 ML is split by a beam splitter (BS). One part (50%) of the output light is detected by a photo diode, and then the intensity fluctuation spectrum of the 1064-nm laser can be captured by the oscilloscope (Tektronic TDS2014C 100 MHz 2 GS/s) after fast Fourier transform. The other part (50%) of the Nd:YVO4 output light is received by the spectrograph (Agilent 86142B 10 pm), which enables us to monitor the laser longitudinal modes.
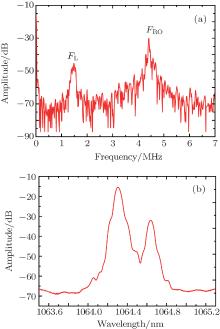
The intensity fluctuation spectrum of Nd:YVO4 ML output is shown in Fig. 2(a). The pump light is 139.2 mW. At the same time, the figure captured by the spectrograph (Fig. 2(b)) indicates that the ML output is of one longitudinal mode. This experimental result proves that there is only one regular RO peak in the intensity fluctuation spectrum of the one-mode laser. In fact, when the pump light is in a range from 60 mW to 151.3 mW, the ML crystal always works at the one-mode oscillation state and the intensity fluctuation spectrum is almost the same as that in Fig. 2(b).
However, when the pump light is beyond 151.3 mW, the Nd:YVO4 ML outputs a two-mode laser as shown in Fig. 3(a) (due to the short cavity, it is very difficult for the laser to output a three-longitudinal-mode laser). The corresponding intensity fluctuation spectrum in Fig. 3(a) is different from the spectrum in one-mode laser. Besides the regular RO peak, one low-frequency RO peak appears in the total intensity fluctuation spectrum. This phenomenon goes against the previous experimental and theoretical results which confirm that the total output intensity fluctuation spectrum in the two-mode laser behaves just like a single-mode laser.[2– 10]
In this section, we build a theoretical model to explain the intensity fluctuation spectra of one-mode and two-mode lasers. Firstly, we use a traditional rate equation model[20] to simulate the intensity fluctuation spectrum of one-mode laser.
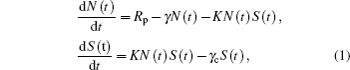
where N (t) is the population inversion; Rp is the steady pumping rate; S (t) is the photon number; K = σ c is the coupling coefficient between N (t) and S (t), with σ being the emission cross-section and c the velocity of light; γ = 1/τ is the decay rate of population inversion and γ c = 1/τ c is the photon decay rate, with τ and τ c being the fluorescence lifetime and photon lifetime, respectively. N (t) and S (t) can be expressed in the following forms:
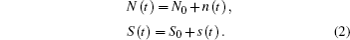
The subscript “ 0” refers to the steady state solutions given by Eq. (1) and n(t), s(t) are perturbation quantities of N0 and S0 which could be obtained by solving Eq. (1) when dN(t)/dt = 0, and dS(t)/dt = 0. After making the perturbation analysis of Eqs. (1) and (2) and neglecting the second order small quantities, the analytical expression of s(t) can be written as

where

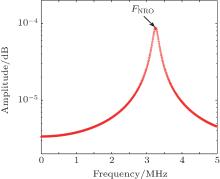
and ω R is the RO frequency. For Nd:YVO4 ML, τ = 90 μ s and σ = 25 × 10− 23 m2. Without loss of generality, assume I = 0.7 and Rp = 3.8 × 1025 s− 1, then we will obtain the intensity fluctuation spectrum of the one-mode laser predicted by Eq. (3) as shown in Fig. 4.
Secondly, for the two-mode laser, the population inversion and the photon inside the laser cavity can be divided into two coupled systems according to two longitudinal modes. Taking the cross-saturation effect into consideration, the two-mode rate equations can be written as

where β is the coefficient between the two systems, and i = 1, 2 denotes two oscillation modes inside the laser cavity. γ is the decay rate of population inversion (the same as those for the two longitudinal modes), γ c1 and γ c2 are the photon decay rate of two oscillation modes, respectively. It is too complex to obtain the analytical solution of Eq. (4), therefore we try to obtain the intensity fluctuation spectra with the numerical method.
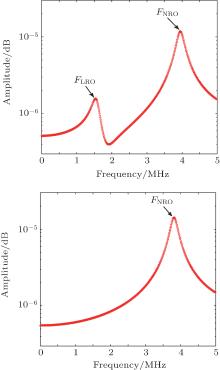
For the Nd:YVO4 microchip laser, τ = 90 μ s, σ = 25 × 10− 23 m2, then γ = 1/τ = 1.11 × 104 s− 1 and K = σ c = 7.5 × 10− 14 m3/s. Due to the standing-wave theory and inhomogenous Nd:YVO4 crystal, the gains and losses for two longitudinal modes in the two-mode laser are different. Without loss of generality, assume Rp1 = 3.5 × 1025 s− 1, Rp2 = 4.0 × 1025 s− 1, γ c1 = 3.6 × 107 s− 1, γ c2 = 3.9 × 107 s− 1, and β = 0.43, then we will obtain the steady state solutions of Eq. (4) by setting the differential terms to be zero. After making the perturbation analysis and performing the numerical solutions to the coefficient matrix, the total intensity fluctuation spectrum of the total output is shown in Fig. 5(a). A notable feature of the total output intensity fluctuation spectrum in the theoretical simulation result is that the low-frequency anti-phase RO peak still appears because FLRO values in individual modes cannot compensate for each other totally. This result goes against the previous work but coincides with our experimental results very well.
If we set gain and loss for two longitudinal modes to be the same values, i.e., Rp1 = Rp2 = 3.5 × 1025 s− 1 and γ c1 = γ c2 = 3.6 × 107 s− 1, we can obtain Fig. 5(b), in which the total intensity fluctuation spectrum behaves like a single mode laser. The phenomenon that low-frequency oscillation RO peaks only appear in the individual mode coincides with previous experimental results and the theoretical prediction.
The previous phenomena and theories involve intensity fluctuation spectra of one-mode and multi-mode lasers. However, nearly all the experimental results and theoretical models indicate that the intensity fluctuation spectra of multi-mode behave like those of a single mode laser although individual intensity spectra show more complex phenomena.
We measure the intensity fluctuation spectra corresponding to the one-mode and two-mode lasers, respectively. For the one-mode laser, classical rate equations are established and analytical solutions are obtained. For two-mode lasers, the population inversion and the photons inside the laser cavity can be divided into two coupled systems according to two longitudinal modes. Taking into account the grating effects of standing-mode patterns in the laser cavity, the two systems are coupled by a coefficient β as shown in Eq. (4). If we set the gains and losses of two longitudinal modes to be the same, we can obtain the same results as shown in Fig. 5(b), which coincide with the previous results very well. However, the actual gains and losses of two longitudinal modes are different due to different wavelengths and different positions of standing-wave inside the cavity. Unlike previous work, low-frequency anti-phase RO can reveal itself in the total output intensity fluctuation spectrum. Rate equations for the one-mode laser and two-mode laser are established, and theoretical simulation results coincide with experimental results very well.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|