†Corresponding author. E-mail: dmdeng@263.net
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11374108 and 10904041), the Foundation for the Author of Guangdong Provincial Excellent Doctoral Dissertation, China (Grant No. SYBZZXM201227), the Foundation of Cultivating Outstanding Young Scholars (“Thousand, Hundred, Ten” Program) of Guangdong Province in China, and the Fund from the Key Laboratory of Geospace Environment, University of Science and Technology of China, Chinese Academy of Sciences.
Under the paraxial approximation, the analytical propagation expression of an Airy–Gaussian beam (AiGB) in uniaxial crystals orthogonal to the optical axis is investigated. The propagation dynamics of the AiGB is given for different ratios of the extraordinary index to the ordinary refractive index. It has been found that the continuity and the self-bending effect of AiGB become weaker when the ratio increases. From the figure of the maximum intensity of AiGB, one can see that the maximum intensity is not monotone decreasing due to the anisotropic effect of the crystals. The intensity distribution of AiGB in different distribution factors is shown. The AiGB converges toward a Gaussian beam as the distribution factor increases.
Dispersion-free Airy wave packets were first predicted theoretically by Berry and Balazs[1] in the context of quantum physics, as a solution of the Schrö dinger equation in 1979. The Airy beam can restore the balance of energy (a self-healing property) after being obscured by an obstacle placed in its propagation path.[2] These beams also have outstanding properties of self-bending and are diffraction-free[3, 4] during propagation. The research of these properties of the Airy beam is only to be applied in optical clearing of microparticles, [5, 6] generating versatile linear bullets, [7] curved plasma channel generation, [8, 9] and vacuum electron acceleration.[10] The initial Airy beam which contains infinite energy is not realizable in practice. Nevertheless, Siviloglou and Chriatodoulides[3, 4] have first observed the new Airy beam that presents a finite energy and demonstrates experimentally the unusual features. The propagation properties of the Airy beam have been researched widely in various mediums. And, the Gaussian beam also has been studied in different cases. Gao et al.[11] have discussed the nonparaxial propagation of phase-flipped Gaussian beams. The propagation factor and the kurtosis parameter of a Gaussian beam with vortex[12] also have reported in 2012. The generalized AiGB, which carries a finite energy and retains the non-diffracting propagation within a finite propagation distance, can be realized experimentally to a very good approximation.[13] In this article, we manage its propagation properties by means of different complex paraxial optical systems characterized by an ABCD matrix.
In the past few years, AiGB has been widely discussed in a quadratic-index medium, [14] in a paraxial optical system, [13] in a Kerr medium, [15] passing through a misaligned optical system with finite aperture, [16] and in the fractional Fourier transform plane.[17] Deng et al.[18] have also studied the analytical vectorial structure of AiGB. It is an interesting subject to describe the light propagation in anisotropic media in both applied and theoretical optics.[19, 20] In fact, they play an outstanding role in the design of optical devices due to crystals’ ability to affect the polarization state of light, such as polarizers and compensators[21] which are commonly employed in many experimental setups. But, the propagation of the AiGB in uniaxial crystal has not been researched.
In this paper, the propagation dynamics of an AiGB is researched analytically and numerically in uniaxial crystals orthogonal to the optical axis. The propagation dynamics of the AiGB is discussed in different proportions of the extraordinary index and the ordinary refractive index. Then the maximum intensity of AiGB in uniaxial crystals is plotted. Finally, we simulate the intensity and the phase distribution of AiGB in different distribution factors.
In the Cartesian coordinate system, the propagation axis is set as the z axis; the x axis is taken to be the optical axis of the uniaxial crystal. The input plane is z = 0 and the observation plane is taken to be z. The dielectric tensor of the uniaxial crystal is depicted as[21– 23]
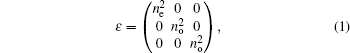
where ne and no are the extraordinary and the ordinary refractive indices of the uniaxial crystal. The electric field distribution of the initial finite energy AiGB is


where Ex (x, y, 0), Ey (x, y, 0) represent the initial electric field distribution in x and y directions. w1, w2 represent arbitrary transverse scales, w1 = w2 = χ 0w0. χ 0 is the distribution factor that makes the beam tend to a Gaussian beam when it is a Barge or an Airy beam when it is small. a, b represent the decay parameter in x and y directions. The total power of this finite energy AiG wave packet reads as

Under the paraxial approximation, in uniaxial crystals, the propagation formulas of the AiGB orthogonal to the optical axis can be given by[19– 21]
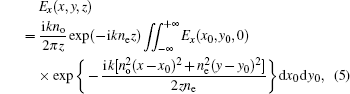
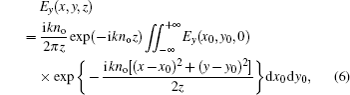
where k = 2π /λ is the wave number, λ is the optical wavelength. Substituting formulas (1) and (2) into formulas (4) and (5), in uniaxial crystals, after propagating a distance z, the analytical complex field of the AiGB orthogonal to the optical axis can be developed as
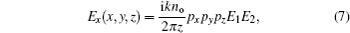
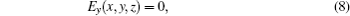
where
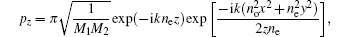
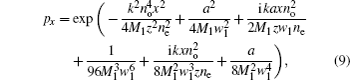
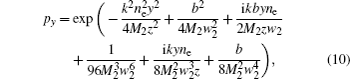
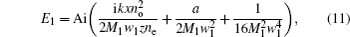
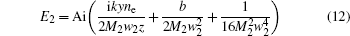
with
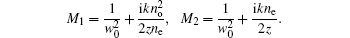
When no = ne= 1, formula (7) becomes the propagation formula of AiGB in free space. It is not difficult to understand that E1 and E2 represent conventional Airy function.
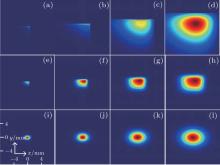
Figure 1 shows the propagation of AiGB in the uniaxial crystals as χ 0 = 10− 4. In calculation, we take a = b = 0.05, w1 = w2 = 10− 4, no = 2.616 with a 633-nm laser. Figure 1 describes the field distribution of the transversal direction when no = ne = 2.616, ne = 1.2no, ne = 1.5no, and ne = 2.0no. Figure 1(a) represents the propagation dynamics of the AiGB when no = ne = 2.616. The properties of the material are isotropic when the extraordinary index is equal to the ordinary index. Evidently this wave endures because of the isotropic properties. Figures 1(b), 1(c), and (d) indicate the propagation dynamics in the case of no not equal to ne. Due to the anisotropic effect of the crystals, the propagation dynamics in Figs. 1(b)– 1(d) is discontinuous. Even more evidently, the ratio of extraordinary and ordinary refractive indices will affect the continuity and the bending degree of AiGB in the process of propagation. The bending of AiGB is caused by the self-accelerated characteristics of the Airy packet.
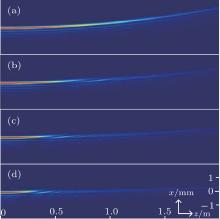 | Fig. 1. Propagation dynamics of AiGB as a function of distance in no = ne = 2.616, no = 1.2ne, no = 1.5ne, no = 2.0ne transeversal directions. |
Figure 2 clearly shows the propagation dynamics of the maximum intensity of the AiGB as a function of the propagation distance. The maximum intensity gets smaller as the distance is increasing. Even more clearly, the maximum intensity of the AiGB is not monotone decreasing due to the anisotropic effect of the crystals.
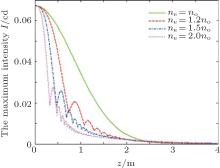 | Fig. 2. Propagation dynamics of the maximum intensity of light of the AiG beams as a function of propagation distance; cd is a unit of luminous intensity. |
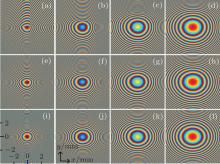
In the research of AiGB, the ratio of Airy beam and Gaussian beam depends on the distribution factor χ 0, χ 0 is an adjustable parameter. In theory, when the distribution factor goes to zero, the AiG beam goes to the field distribution of Airy beams. And, when the distribution factor goes to infinity, the AiGB goes to the field distribution of Gaussian beams. In fact, the field distribution of Airy beams has been exhibited obviously as χ 0= 0.01, the field distribution of Gaussian beams has also been exhibited as χ 0= 1. It is not difficult to get the above point of theories from each column in Fig. 3. Figures 3(i)– 3(l) show obviously that the field distributions of AiGB are elliptic due to the anisotropic effect of the crystals. Each row in Fig. 3 shows the propagation of the AiGB at the positions 1, 2, 3, and 4 m in the uniaxial crystal. The main lobe is rebuilt as the AiGB propagates further in the uniaxial crystal. Figure 4 depicts the corresponding phase distribution.
The effect of the uniaxial crystals on AiGB has been studied under the paraxial approximation. The stimulation of propagation dynamics of AiGB for different ratios of the extraordinary refractive index ne to the ordinary refractive index no is shown. The results tell us that the continuity and the self-acceleration effect of AiGB are made weaker as the proportion increases. As demonstrated in the maximum intensity of AiGB, the maximum intensity is not monotone decreasing due to the anisotropic effect of the crystals. By using the simulations, the intensity distribution of AiGB in different distribution factors is shown. It is known that the AiGB goes to a Gaussian beam as the parameter χ 0 increases.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|