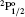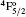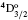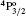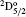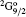Tungsten (W), being an important constituent of tokamak reactor walls, is perhaps the most important element for studying fusion plasmas. It immensely radiates at almost all ionization stages, and therefore to assess radiation loss and for modelling plasmas, atomic data (including energy levels and oscillator strengths or radiative decay rates) are required for many of its ions. The developing ITER project has raised urgency for the data requirements, and as a result several groups of people are engaged in producing atomic data for its ions. However, the most desirable requirement for (any) atomic data is its accuracy^[1] without which the modelling of plasmas will not be reliable. Recently, S. Aggarwal et al., ^[2] henceforth to be referred to as AJM, have reported results for energy levels, oscillator strengths, radiative rates, and lifetimes for Al-like W. For their calculations, they adopted the modified version of the GRASP (general-purpose relativistic atomic structure package) code, available at the website http://web.am.qub.ac.uk/DARC/. It is a fully relativistic code, based on the jj coupling scheme, and hence ideal for generating atomic data for heavier ions, such as of W. Further relativistic corrections arising from the Breit interaction and QED (quantum electrodynamics) effects are also included.

AJM have reported energies and lifetimes (τ ) for the lowest 148 levels of the 3s²3p, 3s3p², 3s²3d, 3s3p3d, 3p³, 3p²3d, 3s3d², 3p3d², and 3d³ (nine) configurations. They have also listed radiative rates (A-values), oscillator strengths (f-values) and line strengths (S-values) for four types of transitions, namely electric dipole (E1), electric quadrupole (E2), magnetic dipole (M1), and magnetic quadrupole (M2), but only from the ground to higher excited levels. However, unfortunately there are several discrepancies and a few serious errors in their paper, and here we focus only on three, discussed below.

Firstly, their use of the nomenclature of the ion (being wrong) in the title and throughout the text of the paper is confusing and misleading. This is because Al-like tungsten is W LXII, and not W XLVII. Secondly, to calculate atomic data they have included configuration interaction (CI) among 894 levels of 35 configurations, the additional 26 are: 3s3p4ℓ , 3s3d4ℓ , 3p3d4ℓ , 3s²4ℓ , 3p²4ℓ (except 3p²4d), 3p4ℓ ² (except 3p4p²), and 3d4ℓ ². However, these 35 configurations generate 1007 levels in total (see Section  2), and hence there is a discrepancy of 113 levels. Both of these discrepancies may, at best, be attributed to oversight and do not affect the calculated results. However, the third and the final one is the gross error in their calculated lifetimes, of up to 14 orders of magnitude for over 90% of the levels — see Section  3. Therefore, the purpose of this comment is to report the correct τ values and to explain the reasons for these large errors.

For our calculations we adopt the same version of the grasp code as employed by AJM.^[2] Similarly, for compatibility we use the same option of extended average level (EAL), as adopted by them. To make comparisons, we have performed two sets of calculations, one with 148 levels of 9 configurations (GRASP1), i.e., 3s²3p, 3s3p², 3s²3d, 3s3p3d, 3p³, 3p²3d, 3s3d², 3p3d², and 3d³; and another with 37 (GRASP2), the additional 28 being 3s3p4ℓ , 3s3d4ℓ , 3p3d4ℓ , 3s²4ℓ , 3p²4ℓ , 3p4ℓ ², and 3d4ℓ ². All these configurations, along with the number of levels generated by each, are listed in Table  1. In total, these configurations generate 1056 levels. AJM included the same configurations (except two) in their calculations (GRASP3), but it is not clear why they ignored 3p²4d and 3p4p². These two configurations (number 28 and 31 in Table  1) generate 49 levels and therefore the number of levels included by AJM should have been 1007 (1056-49), and not 894 as stated by them. However, as far as the calculations of τ (our parameter of interest) are concerned, the inclusion/exclusion of these two configurations is of no consequence as we will see in the next section.

Table 1.

Table 1.

Table 1. Configurations and levels of W LXII. Odd parity levels are indicated by a superscript ‘ o’ . Index Configuration No. of Levels Total No. of Levels 1 3s23p 2° 2 2 3s3p2 8 10 3 3s23d 2 12 4 3s3p3d 23° 35 5 3p3 5° 40 6 3p23d 28 68 7 3s3d2 16 84 8 3p3d2 45° 129 9 3d3 19 148 10 3s3p4s 7° 155 11 3s3p4p 18 173 12 3s3p4d 23° 196 13 3s3p4f 24 220 14 3s3d4s 8 228 15 3s3d4p 23° 251 16 3s3d4d 34 285 17 3s3d4f 39° 324 18 3p3d4s 23° 347 19 3p3d4p 65 412 20 3p3d4d 96° 508 21 3p3d4f 113 621 22 3s24s 1 622 23 3s24p 2° 624 24 3s24d 2 626 25 3s24f 2° 628 26 3p24s 8 636 27 3p24p 21° 657 28 3p24d 28 685 29 3p24f 30° 715 30 3p4s2 2° 717 31 3p4p2 21° 738 32 3p4d2 45° 783 33 3p4f2 69° 852 34 3d4s2 2 854 35 3d4p2 28 882 36 3d4d2 67 949 37 3d4f2 107 1056

Table 1. Configurations and levels of W LXII. Odd parity levels are indicated by a superscript ‘ o’ .

The energies obtained in our calculations for the lowest 148 levels of W LXII are comparable to those reported by AJM in their Table  1, and hence are not repeated here. Similarly, there is no (significant) discrepancy with their A-values, listed in their Table  3. Therefore, we now focus on the τ values for which we find large discrepancies.

The lifetime τ of a level j is determined as τ _j = 1/∑ _i A_ji, i.e., the summation is over all transitions from lower levels i to higher j. Generally, A-values for E1 transitions dominate for the determination of τ , but for other types of transitions, they become important, particularly when the E1 transition does not exist, such as for 1– 3/5/9 (see Table  2 for level definitions). For this reason, A-values from all types of transitions are included in calculations, as was also done by AJM.^[2] In Table  2, we list our calculated τ from both GRASP1 and GRASP2 calculations, and also include the results of AJM (GRASP3) for a ready comparison.

Table 2.

Table 2.

Table 2. Lifetimes (τ , in unit s) for the levels of W LXII. a± b ≡ a × 10± b. Index Configuration Level GRASP1 GRASP2 GRASP3 1 3s23p … … … 2 3s3p2(3P) 4P1/2 2.550− 11 2.538− 11 2.54− 11 3 3s23p 2.071− 09 2.046− 09 4.58− 09 4 3s3p2(3P) 4P3/2 7.446− 11 7.357− 11 8.85− 11 5 3s3p2(1D) 2D5/2 7.026− 11 6.988− 11 6.99− 11 6 3s3p2(1D) 2D3/2 1.448− 12 1.443− 12 1.51− 12 7 3s3p2(3P) 2P1/2 3.493− 13 3.490− 13 3.53− 13 8 3s23d 2D3/2 2.577− 13 2.577− 13 2.58− 13 9 3s23d 2D5/2 3.417− 12 3.425− 12 3.43− 12 10 3p3 4.586− 12 4.601− 12 6.61− 07 11 3s3p(3P)3d 2.148− 12 2.159− 12 3.39− 07 12 3s3p(3P)3d 3.473− 11 3.473− 11 9.26− 04 13 3s3p(3P)3d 4.189− 13 4.195− 13 8.51− 06 14 3s3p(3P)3d 2.863− 13 2.858− 13 4.41− 05 15 3s3p(3P)3d 3.519− 12 3.530− 12 2.69− 06 16 3s3p(3P)3d 4.710− 12 4.715− 12 5.34− 12 17 3s3p(3P)3d 3.871− 12 3.870− 12 8.53− 06 18 3s3p(3P)3d 1.401− 12 1.405− 12 5.22− 06 19 3s3p2(3P) 4P5/2 1.397− 12 1.399− 12 1.40− 12 20 3s3p2(3P) 2S1/2 4.880− 13 4.869− 13 1.32− 10 21 3p23d 1.542− 12 1.518− 12 3.50− 08 22 3s3p2 2P3/2 2.729− 13 2.739− 13 4.35− 10 23 3p23d 4F5/2 3.051− 12 3.066− 12 9.39− 09 24 3p3(2D) 8.241− 13 8.260− 13 6.38− 07 25 3p3(4S) 3.188− 13 3.195− 13 1.33− 04 26 3p3(2P) 4.161− 13 4.163− 13 1.52− 05 27 3s3p(3P)3d 4.181− 13 4.190− 13 1.40− 06 28 3s3p(3P)3d 5.586− 13 5.596− 13 1.24− 06 29 3s3p(3P)3d 3.170− 13 3.177− 13 5.19− 04 30 3s3p(3P)3d 5.970− 13 5.981− 13 6.11− 13 31 3s3p(3P)3d 2.275− 13 2.277− 13 1.19− 05 32 3s3p(3P)3d 1.948− 13 1.961− 13 1.36− 03 33 3s3p(3P)3d 1.746− 13 1.757− 13 3.82− 05 34 3s3p(3P)3d 4.707− 09 4.702− 09 4.85− 09 35 3s3p(3P)3d 1.196− 12 1.206− 12 7.47− 06 36 3s3p(3P)3d 1.826− 12 1.833− 12 9.17− 12 37 3s3p(3P)3d 1.109− 12 1.123− 12 1.19− 04 38 3s3p(1P)3d 4.036− 13 4.087− 13 3.27− 11 39 3s3p(3P)3d 1.243− 12 1.235− 12 1.28− 03 40 3s3p(1P)3d 3.305− 13 3.345− 13 1.59− 06 41 3s3p(1P)3d 3.334− 13 3.346− 13 5.50− 06 42 3p2(1D)3d 2F5/2 9.155− 13 9.226− 13 1.75− 08 43 3p2(3P)3d 4D3/2 5.132− 13 5.172− 13 2.47− 09 44 3p2(3P)3d 4D1/2 4.601− 13 4.648− 13 4.57− 09 45 3p2(1D)3d 2G7/2 6.025− 13 6.109− 13 2.30− 05 46 3p2(1D)3d 2D3/2 2.936− 13 2.941− 13 2.73− 09 47 3p2(3P)3d 2D5/2 3.316− 13 3.330− 13 8.89− 09 48 3p2(3P)3d 4D1/2 3.681− 13 3.674− 13 2.58− 07 49 3s3d2(3F) 4F3/2 2.333− 13 2.348− 13 1.46− 06 50 3s3d2(3F) 4F5/2 2.061− 13 2.072− 13 1.03− 09 51 3p2(3P)3d 4F7/2 6.144− 13 6.203− 13 2.36− 05 52 3p2(1D)3d 2G9/2 1.177− 12 1.183− 12 1.29− 12 53 3s3d2(3P) 4P1/2 1.950− 13 1.979− 13 1.75− 08 54 3p2(1D)3d 2P3/2 6.222− 13 6.253− 13 3.12− 08 55 3p2(1D)3d 2D5/2 6.468− 13 6.516− 13 1.35− 08 56 3p2(1D)3d 2F7/2 9.228− 13 9.346− 13 2.49− 05 57 3p2(3P)3d 4P5/2 4.992− 13 5.063− 13 2.44− 07 58 3p2(1D)3d 2S1/2 8.612− 13 8.652− 13 1.46− 10 59 3p2(3P)3d 2D3/2 5.006− 13 5.067− 13 1.06− 10 60 3s3d2(3F) 4F7/2 3.663− 13 3.693− 13 6.83− 02 61 3s3d2(3P) 4P5/2 4.248− 13 4.292− 13 1.10− 08 62 3s3d2(3P) 4P3/2 4.498− 13 4.552− 13 2.72− 09 63 3s3d2(1G) 2G9/2 3.807− 13 3.873− 13 4.49− 13 64 3s3d2(3F) 2F5/2 2.996− 13 3.023− 13 1.75− 08 65 3s3d2(1G) 2G7/2 4.601− 13 4.678− 13 3.48− 04 66 3s3d2(1D) 2D3/2 3.101− 13 3.141− 13 1.02− 10 67 3s3d2(3P) 2P1/2 2.577− 13 2.619− 13 7.30− 11 68 3p3(2D) 1.695− 13 1.698− 13 1.33− 03 69 3p3d2(1G) 1.782− 12 1.812− 12 3.35− 02 70 3s3d2(3F) 4F9/2 1.447− 12 1.475− 12 7.27− 12 71 3s3d2(1D) 2D5/2 1.232− 12 1.255− 12 3.15− 10 72 3p3d2(3P) 5.100− 13 5.165− 13 7.47− 03 73 3p3d2(3F) 2.800− 13 2.799− 13 1.11− 03 74 3s3d2(3F) 2F7/2 1.194− 12 1.213− 12 9.25− 03 75 3s3d2(3P) 2P3/2 9.842− 13 1.001− 12 2.61− 08 76 3s3d2(1S) 2S1/2 9.985− 13 1.024− 12 1.81− 09 77 3p3d2(3F) 3.497− 12 3.521− 12 2.21− 09 78 3p3d2(3F) 2.370− 12 2.402− 12 5.79− 03 79 3p3d2(3P) 2.426− 12 2.454− 12 3.42− 04 80 3p3d2(3P) 2.505− 12 2.531− 12 7.52− 05 81 3p3d2(1G) 3.533− 12 3.570− 12 8.28− 06 82 3p3d2(3F) 3.968− 13 3.965− 13 5.87+ 01 83 3p3d2(1G) 4.454− 13 4.522− 13 3.28− 08 84 3p3d2(3P) 3.570− 13 3.611− 13 5.11− 05 85 3p23d(2D) 4P3/2 1.778− 13 1.789− 13 3.50− 08 86 3p23d(2D) 4D5/2 1.847− 13 1.864− 13 1.27− 08 87 3p23d(2D) 2P1/2 1.745− 13 1.759− 13 4.77− 09 88 3p23d(2D) 2F7/2 1.926− 13 1.949− 13 4.33− 06 89 3p3d2(3F) 1.715− 12 1.735− 12 2.75− 08 90 3p3d2(3F) 2.438− 12 2.450− 12 3.83− 01 91 3p3d2(1D) 1.571− 12 1.585− 12 5.55− 03 92 3p3d2(3P) 1.876− 12 1.890− 12 1.23− 03 93 3p23d(2D) 2D3/2 1.882− 13 1.900− 13 2.85− 09 94 3p23d(2D) 4D1/2 1.342− 12 1.375− 12 1.98− 01 95 3p23d(2D) 4F9/2 2.808− 13 2.842− 13 2.75− 09 96 3p23d(2D) 4D7/2 2.637− 13 2.668− 13 6.13− 05 97 3p23d(2D) 2P1/2 2.369− 13 2.395− 13 1.48− 07 98 3p23d(2D) 2D5/2 2.621− 13 2.653− 13 1.49− 10 99 3p23d(2D) 2P3/2 2.244− 13 2.275− 13 9.46− 04 100 3p23d(2D) 2F5/2 2.305− 13 2.334− 13 3.18− 10 101 3p3d2(3F) 1.876− 13 1.894− 13 4.84− 02 102 3p3d2(3F) 1.979− 13 2.001− 13 2.73− 03 103 3p3d2(3F) 1.857− 13 1.874− 13 1.85− 02 104 3p3d2(3F) 2.060− 13 2.084− 13 4.13− 09 105 3p3d2(3P) 1.871− 13 1.902− 13 2.73− 03 106 3p3d2(3F) 3.026− 13 3.069− 13 3.20− 06 107 3p3d2(3P) 2.832− 13 2.870− 13 3.31− 10 108 3p3d2(3P) 2.753− 13 2.798− 13 5.42− 05 109 3p3d2(1G) 3.523− 13 3.600− 13 2.94− 04 110 3p3d2(3P) 2.568− 13 2.600− 13 1.71− 02 111 3p3d2(3F) 2.543− 13 2.577− 13 9.28− 03 112 3p3d2(3F) 2.638− 13 2.675− 13 2.02− 01 113 3p3d2(1G) 2.888− 13 2.938− 13 6.64− 10 114 3p3d2(3F) 2.668− 13 2.711− 13 1.81− 09 115 3p3d2(3P) 2.520− 13 2.559− 13 2.37− 04 116 3p3d2(1D) 2.444− 13 2.476− 13 1.43− 02 117 3p3d2(1G) 2.828− 13 2.883− 13 1.03− 05 118 3p3d2(3P) 2.469− 13 2.513− 13 2.04− 01 119 3p3d2(1G) 2.591− 13 2.642− 13 5.34− 04 120 3p3d2(3P) 2.444− 13 2.485− 13 3.23− 02 121 3p3d2(3F) 5.601− 13 5.737− 13 1.81− 05 122 3p3d2(1D) 4.432− 13 4.524− 13 3.29− 03 123 3p3d2(1D) 4.900− 13 5.005− 13 9.14− 10 124 3p3d2(3F) 4.476− 13 4.555− 13 5.21− 05 125 3p3d2(1D) 3.904− 13 3.975− 13 8.02− 00 126 3p3d2(3F) 3.816− 13 3.895− 13 6.02− 09 127 3p3d2(1S) 4.347− 13 4.459− 13 7.53− 03 128 3p3d2(3F) 3.792− 13 3.872− 13 3.51− 03 129 3p3d2(3P) 3.470− 13 3.546− 13 1.11− 02 130 3d3(4F) 4F3/2 1.940− 13 1.952− 13 6.38− 07 131 3d3(4F) 4F5/2 2.735− 13 2.755− 13 1.08− 06 132 3d3(4P) 4P3/2 2.626− 13 2.641− 13 5.31− 05 133 3d3(2H) 2H9/2 3.068− 13 3.128− 13 1.96− 09 134 3d3(2G) 2G7/2 2.896− 13 2.935− 13 6.02− 03 135 3d3(2D) 4P1/2 2.584− 13 2.594− 13 5.77− 06 136 3d3(4P) 2D5/2 2.631− 13 2.655− 13 8.65− 06 137 3d3(4F) 4F7/2 4.503− 13 4.544− 13 5.76− 03 138 3d3(4F) 4F9/2 4.904− 13 4.983− 13 4.82− 10 139 3d3(2D) 2D3/2 4.274− 13 4.305− 13 1.62− 06 140 3d3(2P) 2P1/2 4.102− 13 4.117− 13 6.84− 05 141 3d3(2H) 2H11/2 5.645− 13 5.832− 13 1.17− 05 142 3d3(4P) 4P5/2 3.976− 13 3.994− 13 8.09− 09 143 3d3(2D) 2D5/2 4.565− 13 4.641− 13 8.94− 06 144 3d3(2F) 2F7/2 4.730− 13 4.831− 13 1.27− 02 145 3d3(2D) 2D3/2 4.373− 13 4.436− 13 1.35− 06 146 3d3(2G) 2G9/2 1.286− 12 1.302− 12 1.39− 09 147 3d3(4P) 2P3/2 1.031− 12 1.041− 12 2.43− 05 148 3d3(2F) 2F5/2 9.786− 13 9.848− 13 5.25− 07 GRASP1: present calculations with the GRASP code with 148 levels, GRASP2: present calculations with the GRASP code with 1056 levels, GRASP3: earlier calculations of S. Aggarwal et al.[2]  with the GRASP code with 894 levels.

Table 2. Lifetimes (τ , in unit s) for the levels of W LXII. a± b ≡ a × 10± b.

For all 148 levels listed in Table  2, there is no (appreciable) discrepancy between the GRASP1 and GRASP2 results. Therefore, as stated earlier, the inclusion or exclusion of the 3p²4d and 3p4p² configurations, omitted by AJM, is of no consequence, and hence the values of τ calculated by AJM should have been comparable to those of ours. Unfortunately, there are large discrepancies for almost all levels, over 90% to be precise. For all levels, the reported values of τ by AJM are invariably higher, by up to 14 orders of magnitude, see for example levels 11, 12, 25, 26, 37, and 82. Below we explain the possible reasons for these large discrepancies.

For level 3 the τ by AJM is higher by a factor of two. For this level, the AJM calculation appears to include only the A-value (2.18 × 10⁸  s^{− 1}) for the 1– 3 M1 transition (see their Table  3), whereas the A-value for the 2– 3 E1 transition (2.64 × 10⁸  s^{− 1}, not listed by AJM), has been completely ignored. Similarly for level 11 their calculation is based on the A-value (2.95 × 10⁶  s^{− 1}) of 1– 11 M1 transition alone. Interestingly, they have also listed the A-value for the 1– 11 E2 transition, i.e., 9.38 × 10⁶  s^{− 1}. The inclusion of these two A-values alone will give τ = 8.1 × 10^{− 8}  s, and not 3.39 × 10^{− 7}  s, as listed by them in their Table  1. However, the correct value for this level is ∼ 2.1 × 10^{− 12}  s, as listed in our Table  2. This is because the main contributing transitions are: 2– 11 E1 (A = 3.72 × 10¹¹  s^{− 1}), 5– 11 E1 (A = 5.26 × 10¹⁰  s^{− 1}), and 6– 11 E1 (A = 3.29 × 10¹⁰  s^{− 1}). Finally, the largest discrepancy of 14 orders of magnitude is for level 82, i.e., . For this level, AJM have listed A = 3.66 × 10⁵  s^{− 1} for the 1– 82 E2 transition, which alone gives τ = 2.73 × 10^{− 6}  s, and not 5.87 × 10¹  s, as listed by them in their Table  1. For this level the dominant contributing transition is 23– 82 E1 for which A = 2.24 × 10¹²  s^{− 1}, giving τ = 4.46 × 10^{− 13}  s, a value within ∼ 10% of that listed in the present Table  2. Therefore, it is abundantly clear that the τ values reported by AJM^[2] are simply wrong for most of the levels.

In this work, we have calculated energy levels, radiative rates and lifetimes for the lowest 148 levels/transitions of Al-like tungsten, i.e., W LXII. For the calculations, the well-known grasp code has been adopted, as by S. Aggarwal et al.^[2] who have recently reported similar results. However, their results for energy levels and A-values (although for limited transitions) are correct, the corresponding values of τ are in huge errors, of up to 14 orders of magnitude, for almost all levels. In fact, their reported τ values appear to have no relationship with the A-values for transitions of this ion. Therefore, for the benefit of users as well as for future workers, we have listed the correct values of τ , and have also explained the reasons for discrepancies. Apart from the errors in τ , other discrepancies in the paper of AJM have been noted. However, we stress that the listed anomalies are not the only ones, there are a few more. As an example, the 101– 129 levels listed in their Table  1 have no (odd) parity indication.

Finally, the A-values listed by S. Aggarwal et al.^[2] for transitions from the ground level alone are not sufficient for applications, because a complete set of data for all transitions are required for any modelling application. Besides this, there is scope for improvement in their work, because in their CI calculations they have ignored the inclusion of some of the important configurations, such as 3p²4d, 3p4p², 3d²4ℓ , and 3ℓ 4ℓ ℓ ′ , apart from those of n = 5. Therefore, an improved set of complete data for all transitions of W LXII are reported in a separate paper.^[3]