†Corresponding author. E-mail: hyj0507@zjut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61374094 and 61503338) and the Natural Science Foundation of Zhejiang Province, China (Grant No. LQ15F030005).
In this paper, the multistability issue is discussed for delayed complex-valued recurrent neural networks with discontinuous real-imaginary-type activation functions. Based on a fixed theorem and stability definition, sufficient criteria are established for the existence and stability of multiple equilibria of complex-valued recurrent neural networks. The number of stable equilibria is larger than that of real-valued recurrent neural networks, which can be used to achieve high-capacity associative memories. One numerical example is provided to show the effectiveness and superiority of the presented results.
In the past few decades, recurrent neural networks with their various generalizations have been extensively investigated due to their potential applications in pattern classification, associative memory, reconstruction of moving images, signal processing, parallel computation, and solving some classes of optimization problems.[1– 5] Associative memories are brain-style devices, which are designed to memorize a set of patterns such that the stored patterns can be retrieved with the initial probes containing sufficient information about the patterns. In the associative memory based on recurrent neural networks, the stable output vectors are designed as the desired patterns. Hence, coexistence of many equilibria is a necessary feature in the applications of neural networks to associative memory storage and pattern recognition. Multistability of real-valued recurrent neural networks has been extensively investigated.[6– 13]
As the extension of real-valued recurrent neural networks, complex-valued recurrent neural networks have been investigated.[14– 20] Complex-valued recurrent neural networks have specific applications different from those in real-valued recurrent neural networks. Complex-valued recurrent neural networks are most suitable for robotics having rotational articulation, wave information processing where the phase carries primary information, etc. Although a complex number is presented as an ordered pair of two real numbers, the most significant advantage of complex-valued neural networks originates not from the two-dimensionality of the complex plane, but from the fact that the multiplication of the synaptic weights, which is the elemental process at the synapses of neurons that construct the whole network.[21] This fact reduces the degree of freedom in learning and self-organization, in comparison with a double-dimensional real-valued neural network. Complex-valued recurrent neural networks extend the application fields steadily. General associative memories are also making progress in their improvement.[22] However, to the best of the authors’ knowledge, multistability for complex-valued recurrent neural networks was seldom considered.
It is well known that activation functions play an important role in the dynamical analysis of recurrent neural networks. Dynamics of neural networks rely heavily on the structures of activation functions. Two kinds of activation functions have been considered for recurrent neural networks, that is, the continuous activation functions and the discontinuous activation functions, respectively. As is well known, recurrent neural networks with discontinuous activation functions are important and do frequently arise in applications when dealing with dynamical systems possessing high-slope nonlinear elements. For this reason, much effort has been devoted to analyzing the dynamical behavior of neural networks with discontinuous activation functions.[23– 26] However, multistability for complex-valued recurrent neural networks with discontinuous real-imaginary-type activation functions was seldom considered.
It is well known that time delays of neural networks are unavoidable because of the finite speed of a signal’ s switch and transmission. Therefore, the studies of delayed systems have become a hot topic of great theoretical and practical importance.[27– 30]
Multistability of recurrent neural networks is an important issue when it comes to associative memories. Increasing storage capacity is a fundamental problem. The stable output vectors of neural networks are designed as the desired patterns. Hence, the number of stale equilibria is expected to be very large. Because the parameters of complex-valued recurrent neural networks are composed of real parts and imaginary parts, which can have more stable equilibria than real-valued recurrent neural networks. Meanwhile, discontinuous complex-valued activation functions, in which the real parts and imaginary parts are piecewise constants, can make neural networks have more stable equilibria and larger attractive basins than continuous complex-valued activation functions, in which the real parts and imaginary parts are piecewise linear. Therefore, it is important to explore the existence and stability of multiple equilibria for complex-valued recurrent neural networks with discontinuous real-imaginary-type activation functions.
Motivated by the above consideration, the purpose of this paper is to explore the existence and stability of multiple equilibria for delayed complex-valued recurrent neural networks with discontinuous real-imaginary-type activation functions. The main contributions of this paper are depicted as follows. (i) A special class of discontinuous complex-valued activation functions is proposed. The real part and imaginary part of the activation function are piecewise constants. (ii) Sufficient conditions for the existence of stable equilibria for complex-valued recurrent neural networks with discontinuous real-imaginary-type activation functions are established. Based on the discussion of this paper, more stable equilibria of neural networks will be derived by using complex-valued parameters and discontinuous activation functions. Such a neural network is suitable for synthesizing high-capacity associative memories.
The remainder of this paper consists of the following sections. Section 2 describes some preliminaries and problem formulations. The main results are stated in Section 3. One example is used to show the effectiveness of the obtained results in Section 4. Finally, in Section 5, we draw our conclusions.
In this paper, we consider the following n-neuron complex-valued recurrent neural networks with constant delays
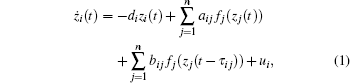
where i = 1, 2, … , n; z(t) = (z1(t), z2(t), … , zn(t))T∈ 
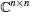
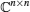
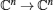

In the complex domain, according to Liouville’ s theorem, [31] if f (z) is bounded and analytic at all z ∈ 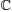
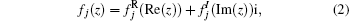
where
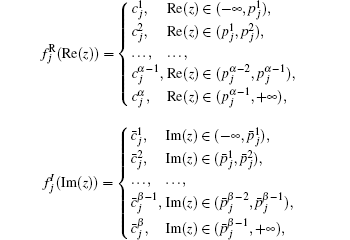
in Eq. (2) i denotes the imaginary unit, i.e. 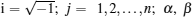
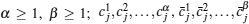
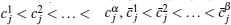
Since the real part and imaginary part of activation function (2) have individual properties, we can separate system (1) into its real and imaginary parts. By separating the state, the connection weight, the activation function, and the external input, we get a real part xi(t) and an imaginary part yi(t) for zi(t), respectively; 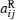
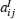
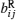

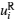
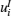
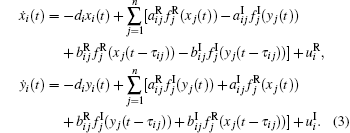
Since 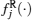
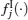
Definition 1 A function
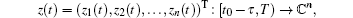
T ∈ (t0, + ∞ ] is a solution of system (1) on [t0 − τ , T) if, i) z(t) is continuous on [t0 − τ , T] and absolutely continuous on [t0, T); ii) there exist measurable functions
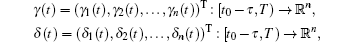
such that 


for a.a. t ∈ [t0, T), where xi(t) = Re(zi(t)), yi(t) = Im(zi(t)), K[E] represents closure of the convex hull of E.
Definition 2 (Initial value problem) For any continuous functions
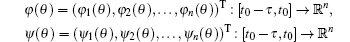
and any measurable selections

such that 
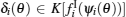
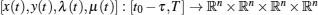

where K[E] represents closure of the convex hull of E.
Definition 3 The equilibrium point z̄ of system (1) is said to be locally exponentially stable in region ⅅ , if there exist constants α > 0, β > 0 such that for any t ≥ t0 ≥ 0,
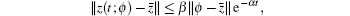
where z(t; ϕ ) is the solution of system (1) with any initial condition ϕ (s), s ∈ 𝒞 ([t0 − τ , t0], ⅅ ).
Lemma 1[33] Let ⅅ be a bounded and closed set in ℝ n, and H be a mapping on complete matric space (ⅅ , ‖ · ‖ ), where for any x, y ∈ ⅅ , | | x − y| | = max1 ≤ i ≤ n {| xi − yi| } is measurement in ⅅ . If H(ⅅ ) ⊂ ⅅ and there exists a positive constant α < 1 such that for any x, y ∈ ⅅ , | | H(x) − H(y)| | ≤ α | | x − y| | , then there exists a unique x̄ ∈ ⅅ such that H(x̄ ) = x̄ .
For the convenience of description, denote 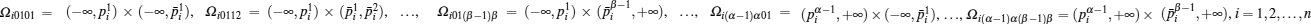
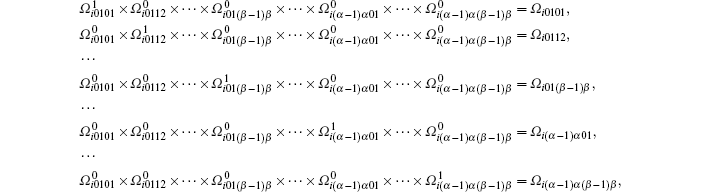
for i = 1, 2, … , n. Denote
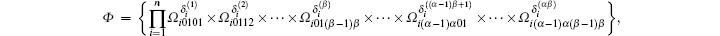
where
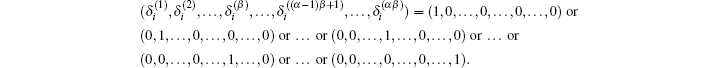
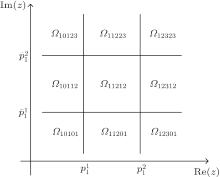
It is easy to see that Φ is composed of (α β )n subregions. In particular, when n = 1, α = β = 3, Φ is composed of 9 subregions (see Fig. 1).
In this section, we will investigate the existence and stability of multiple equilibria for complex-valued recurrent neural network (1) with discontinuous activation function (2). Sufficient criteria will be proposed to ensure system (1) can have (α β )n locally exponentially stable equilibria.
By the partition of the state space and Lemma 1, the following theorem can be derived.
Theorem 1 There exist (α β )n equilibria for system (1) with activation function (2), if the following conditions hold,
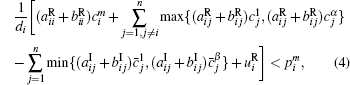

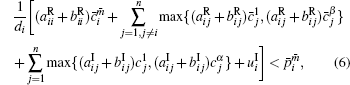
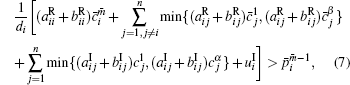
where i = 1, 2, … , n, m = 1, 2, … , α , m̄ = 1, 2, … , β .
Proof According to conditions (4)– (7), there exists a small constant 
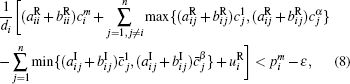
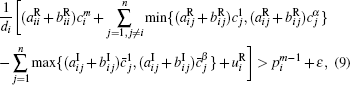
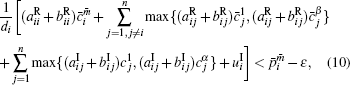
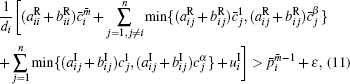
where i = 1, 2, … , n, m = 1, 2, … , α , m̄ = 1, 2, … , β .
For the convenience of description, denote
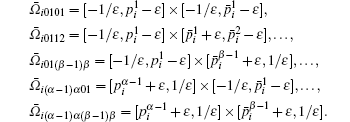
let
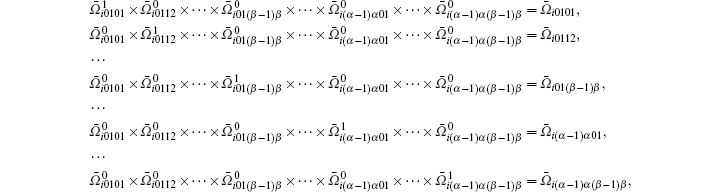
for i = 1, 2, … , n. Denote
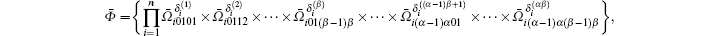
where
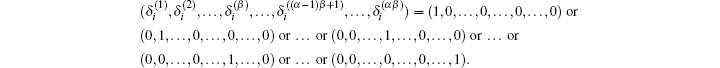
It is obvious that 
For any subregion Ω ⊂ 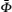
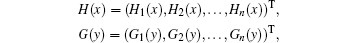
where
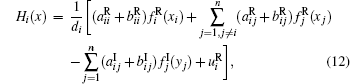
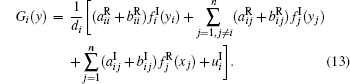
We will show that H(Ω 1) ⊂ Ω 1, G(Ω 2) ⊂ Ω 2. For any x = (x1, x2, … , xn)T ∈ Ω 1, xi belongs to one of the following three cases.
Case 1
Case 2 There exists m ∈ {2, 3, … , α − 1} such that 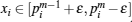
Case 3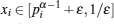
When 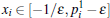
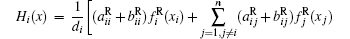
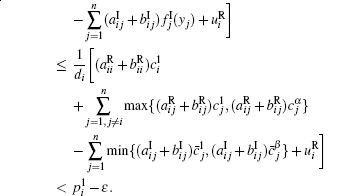
Therefore, 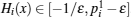
When 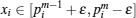
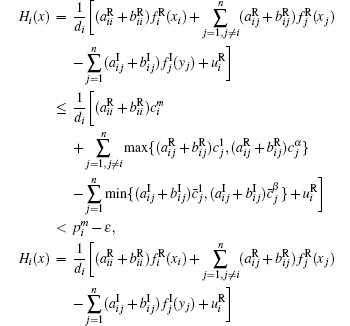
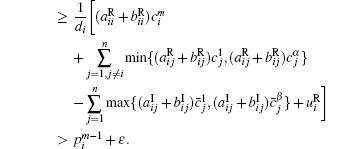
Therefore, 
When 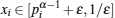
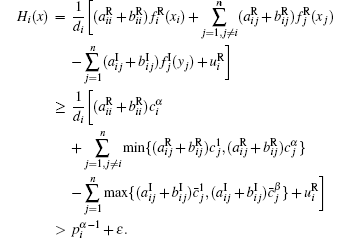
Therefore, 
Based on the above discussion and the arbitrariness of x, we can derive H(Ω 1) ⊂ Ω 1. Similarly, it also holds that G(Ω 2) ⊂ Ω 2. For any 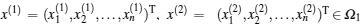
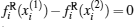
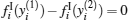
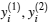
Remark 1 Conditions (4)– (7) assure each subregion of Φ has one equilibrium point. These equilibria exist at the same time. The number of equilibria replies on α and β of the activation function. Therefore, activation functions have an important influence for the existence of multiple equilibria.
Next, we investigate the stability of multiple equilibria for system (1) with activation function (2).
Theorem 2 There exist (α β )n locally exponentially stable equilibria for system (1) with activation function (2), if conditions (4)– (7) hold.
Proof For any subregion Ω ⊂ Φ , according to Theorem 1, there exists an equilibrium point z̄ = x̄ + iȳ , (x̃ , ȳ ) ∈ Ω . Let v(t) = z(t) − z̄ . When (x(t), y(t)) ∈ Ω , 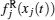
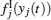
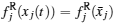
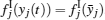
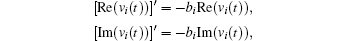
which implies z̄ is locally exponentially stable. Due to the arbitrariness of Ω , we conclude that system (1) has (α β )n locally exponentially stable equilibria, which are located in each invariant subregion of Φ . The proof is completed.
Remark 2 It can be seen that all equilibria in Φ are locally exponentially stable. Each subregion of Φ is an attractive basin of a stable equilibrium point. Stable output vectors can be designed as desired patterns in associative memory. In order to achieve high-capacity associative memory, the number of stable equilibria is expected to be large. In Theorem 2, conditions (4)– (7) ensure each equilibrium point of Φ is stable. Therefore, such complex-valued recurrent neural networks with discontinuous real-imaginary-type activation functions are suitable for synthesizing high-capacity associative memories.
For the case of system (1) without delay, i.e., bij = 0, i, j = 1, 2, … , n, we have the following corollary by using Theorem 1 and Theorem 2.
Corollary 1 There exist (α β )n locally exponentially stable equilibria for system (1) without delay and with activation function (2), if the following conditions hold,
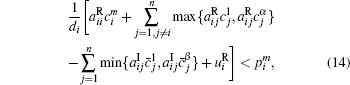
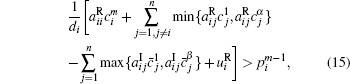
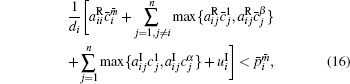
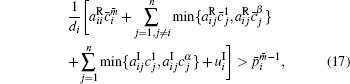
where i = 1, 2, … , n, m = 1, 2, … , α , m̄ = 1, 2, … , β .
In particular, when yi = 0, 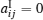
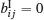
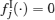
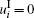
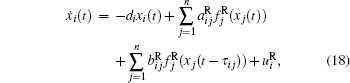
where i = 1, 2, … , n.. By using Theorem 1 and Theorem 2, we can derive the following corollary.
Corollary 2 There exist α n locally exponentially stable equilibria for system (18) with activation function (2), if the following conditions hold,
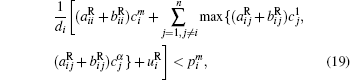
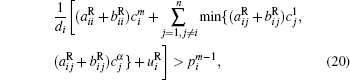
where i = 1, 2, … , n, m = 1, 2, … , α .
Remark 3 Due to the two-dimensionality of the complex plane, real-valued recurrent neural networks can only be seen as one special case of complex-valued recurrent neural networks. Multistability of system (18) has been investigated in Refs. [9] and [10]. Hence, Theorem 1 and Theorem 2 are the improvement and extension of the existing stability results about real-valued recurrent neural networks in the literature.
Remark 4 In this paper, the number of locally exponentially stable equilibria is (α β )n, which is larger than kn in Ref. [25], where α ≥ 1, β ≥ 1, k ≥ 1. Hence, complex-valued neural networks (1) are more suitable for high-capacity associative memories than real-valued neural networks.
In this section, we will give one example to illustrate the effectiveness of our results.
Consider the following 2-neuron complex-valued neural network,
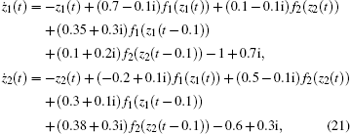
where the discontinuous activation function f1(· ) = f2(· ) = fR(· ) + fI(· )i,
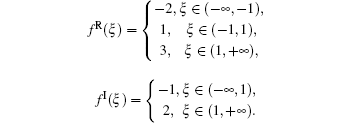
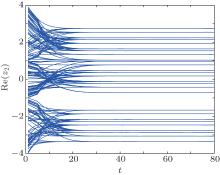
System (21) satisfies conditions (4)– (7). According to Theorems 1 and 2, system (21) has 36 locally exponentially stable equilibria. The dynamics of system (21) are illustrated in Figs. 2– 5, where evolutions of 110 initial conditions have been tracked.
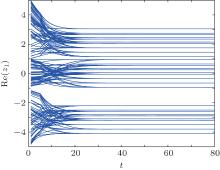 | Fig. 2. State trajectories of Re(z1(t)) of system (21). |
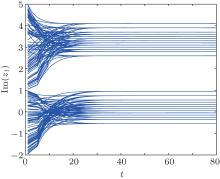 | Fig. 3. State trajectories of Im(z1(t)) of system (21). |
From Figs. 2– 5, it can be seen that the real part and the imaginary part of each neuron state of system (21) converge into one of 36 locally stable states, respectively. Stable states corresponding to the real parts of neuron states locate in (− ∞ , − 1), (− 1, 1), and (1, + ∞ ). Each interval has 12 stable states. Stable states corresponding to imaginary parts of neuron states locate in (− ∞ , 1) and (1, + ∞ ). Each interval has 18 stable states. The partition of these intervals is related with the segmented interval of the real part and the imaginary part of the activation function. Each stable state is related with the value of the activation function. For example, according to the following stationary equation of system (21),
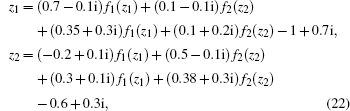
the stable state of Re(z1) with the initial state located in (− ∞ , − 1) is decided by fI(Im(z1)), fR(Re(z2)), fI(Im(z2)). The combination of these three functions has 12 results. Therefore, there exist 12 stable states of Re(z1) in (− ∞ , − 1).
 | Fig. 5. State trajectories of Im(z2(t)) of system (21). |
When all delays are zero, system (21) becomes the following system,
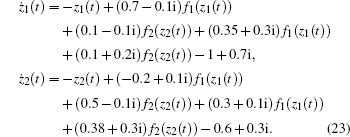
System (23) satisfies conditions (14)– (17). According to the Corollary 1, system (23) still has 36 locally exponentially stable equilibria. It can be seen clearly that delays cannot affect the number of equilibria,
The authors investigated the multistability of 2-neuron real-valued neural networks with a 3-level discontinuous activation function in the simulation example of Ref. [25]. There were 9 locally exponentially stable equilibrium points in Ref. [25], which is less than 36 locally exponentially stable equilibria in the example of this paper. So, complex-valued neural networks are more suitable for high-capacity associative memories than real-valued neural networks.
In this paper, we have discussed the multistability issue of delayed complex-valued recurrent neural networks. A special class of discontinuous real-imaginary-type activation functions has been proposed. By using this neural network model, sufficient criteria have been established to ensure the existence of (α β )n locally exponentially stable equilibria. The number of stable equilibria is larger than that of real-valued recurrent neural networks. Several extensions would be welcome in future works: such as, studying the influence of delay on the attractive basins of stable equilibria of complex-valued recurrent neural networks, and studying the design procedures of achieving associative memories by using multistability results of delayed complex-valued recurrent neural networks in this paper.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|