Molybdenum disilicide (MoSi₂) is a promising candidate material for high temperature structural applications, such as in aircraft gas turbine engines, for its high melting temperature (T_m = 2293  K), relatively low density, excellent high temperature oxidation resistance, and high thermal conductivity.^{[1– 5]} However, MoSi₂ has a low fracture toughness at room temperature (2  MPa· m^1/2– 3  MPa· m^1/2) and low creep strength at elevated temperature. It is observed that the creep stress exponents of polycrystalline MoSi₂ with different grain sizes under stress 50  MPa– 200  MPa at 1473  K are in a range of 2– 9, ^[6] and the creep activity energy is about 430  kJ/mol.^[7] The creep resistance of MoSi₂ drops sharply beyond 1473  K due to enhanced plasticity from the activation of more than five independent slip systems.^[6] These disadvantages greatly hinder  the applications of MoSi₂ for load-bearing, hot section components.

It has been recently reported that these mechanical properties can be improved by alloying with certain elements, such as Al, ^{[8– 10]} Cr, ^{[11– 13]} W, ^{[14, 15]} and Nb.^{[13, 15– 18]} The addition of Al is found to reduce the yield strength of MoSi₂ at all temperatures, improve the low temperature deformability, ^[19] and increase to 4  MPa· m^1/2∼ 6  MPa· m^1/2 in fracture toughness at room temperature.^[20] The addition of Cr has no obvious effect on the fracture toughness, ^[21] but can increase the yield strength at high temperatures (above 1573  K). Moreover, the additions of A1 and Cr can prevent and mitigate the pesting oxidation due to these elements having a strong affinity to oxygen.^[21] W can increase the yield strength at all temperatures, and reduce effectively the high temperature (1473  K) creep rate.^[22] Nb was found to be the most potent alloying element in improving the mechanical properties of MoSi₂.^[23] Nb is the most effective in improving the low temperature deformability and high temperature strength of MoSi₂, and can increase obviously fracture toughness.^[19]

Site occupancy behaviors of these ternary elements are believed to be critical in achieving the improvement. Owing to the extreme difficulty in directly characterizing point defects in an experiment, first-principles approaches^{[24– 27]} have emerged in recent years as an indispensable tool to provide useful insights into point defect thermodynamics.^{[28– 31]} In this paper, we focus on the site occupancy preference and thermodynamic equilibrium concentrations of Al, Cr, W, and Nb in C11_b MoSi₂, particularly as a function of temperature and alloy composition, through integrating the statistical mechanical thermodynamics model and first-principles calculations.

All first-principles calculations are performed based on density functional theory (DFT) as implemented in the VASP code.^{[32, 33]} The electron-core interaction is described by the projector augmented wave method (PAW)^[34] within the frozen-core approximation. According to our previous work, ^[28] the generalized gradient approximation of the Perdew– Burke– Ernzerhof (PBE)^[35] approach is regarded as an appropriate exchange-correlation functional and then employed in this work. The plane-wave basis sets are generated with valence configurations of Mo-4p⁶4d⁵5s¹, Si-3s²3p², Al-3s²3p¹, Cr-3d⁵4s¹, W-5p⁶6s²5d⁴, and Nb-4s²4p⁶5s¹4d⁴, respectively. The plane wave cutoff energy of 400  eV was found to be sufficient and also efficient in our previous work, ^[28] and thus is used throughout this work. The computations are performed based on a 48-atom 2× 2× 2 periodic simulation cell. In order to test the cell size effects, we also calculate the formation enthalpies of isolated point defects within a 162-atom 3 × 3 × 3 periodic cell. The obtained formation enthalpies of Mo vacancy, Mo anti-site, Si vacancy and Si anti-site are 3.628  eV, 3.535  eV, 5.440  eV, and 2.343  eV, respectively. These values are all slightly higher than 3.536  eV, 3.470  eV, 5.309  eV, and 2.310  eV of the 48-atom system reported in our previous work.^[28] These differences are generally less than 0.1  eV except for the Si vacancy (0.131  eV), and it indicates that the 48-atom cell is sufficient to give converged results. Moreover, the 32-atom system and even a system with less atoms have been used in other studies, such as Refs.  [29] and [30], and it has been proved that the results of the 2× 2× 2 periodic simulation cell in the statistic model are acceptable and credible. In this work, the point defect calculations are performed within a 48-atom (16Mo, 32Si) C11_b MoSi₂ conventional supercell with an 8× 8× 3 Monkhorst– Pack k-mesh^[36] for the Brillouin zone integration. During calculations, both cell parameters and internal parameters are relaxed simultaneously to minimize the Hellman– Feymann force on each atom with a tolerance value of 0.02  eV/Å .

MoSi₂ has a body-centered tetragonal C11_b structure up to 1900  ° C (space group I4/mmm). A unit cell of C11_b MoSi₂ consists of two Mo and four Si atoms, with Mo located at the Wyckoff 2a site (0, 0, 0) and Si at the 4e site (0, 0, u). The lattice parameters have been experimentally determined to be a = 3.2056  Å , c = 7.8450  Å , and u = 0.3353  c.^[37] Point defects in C11_b MoSi₂ can be assumed to be sufficiently dilute, which allows the Wagner– Schottky model^{[30, 31, 38]} to be used to predict the point defect concentrations and other relevant thermodynamic functions.

According to the Wagner– Schottky assumption, the formation energy of the compound depends linearly on defect concentration, or alternatively, the formation enthalpies of point defects can be obtained by finite differencing from fully-ordered stoichiometric MoSi₂ as^{[28– 31, 38]}

where H_iα is the formation enthalpy of species i on the a sublattice with a = {Mo, Si} and i = {Mo, Si, V, X} (here V denotes vacancy, and X represents the alloying element, such as Al, Cr, W, and Nb), Δ H_def is the formation enthalpy (per formula unit) of a 48-atom C11_b MoSi₂ conventional supercell containing a single point defect (V_Mo, V_Si, Mo_Si, Si_Mo, X_Mo, and X_Si), Δ H_perf is the formation enthalpy of a perfectly ordered defect-free MoSi₂ in its C11_b structure, and c_iα is the concentration of species i on a sublattice. Note that c_iα = 1/48 for an anti-site defect or a ternary substitution, and 1/47 for a vacancy in the 48-atom supercell.

For a doped MoSi₂, Δ H_def depends sensitively on doping concentration. The formation enthalpy of Mo_pSi_qX_r with an arbitrary composition can be calculated as

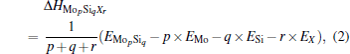
where E_Mo, E_Si, E_X, and E_MopSiqXr are, respectively, the calculated total energies of pure Mo, Si, X, and the doped compound Mo_pSi_qX_r; p, q, and r are the molar compositions of Mo, Si, and X. The formation enthalpies of isolated point defects used in the present calculation are listed in Table  1. In Table  1, the formation enthalpies of Si anti-site (Si_Mo), Mo anti-site (Mo_Si), Mo-vacancy (V_Mo), and Si-vacancy (V_Si) have been calculated in our previous work, ^[28] and the formation enthalpies of two site occupations for Al, Cr, W, and Nb are calculated in this work. From Table  1, we find that the calculated formation enthalpies are relatively high, and it may be related to the strong covalent bonds caused by the hybridization of Mo-4d and Si-3p orbitals.^[28]

Table 1.

Table 1.

Table 1. Formation enthalpies of isolated point defects of stoichiometric C11b MoSi2 used in the present calculation (in units of eV). Designation VMo VSi MoSi SiMo AlMo AlSi CrMo CrSi WMo WSi NbMo NbSi Formation enthalpy 3.54 2.31 3.47 5.31 3.79 0.19 0.72 2.88 0.53 3.76 0.25 2.70

Table 1. Formation enthalpies of isolated point defects of stoichiometric C11b MoSi2 used in the present calculation (in units of eV).

Micro-changes of the point defect concentrations correspond to some defect reactions, and these defect reactions can be described by

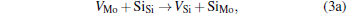
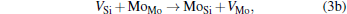
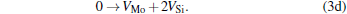
The equilibrium concentrations of point defects can be estimated by minimizing the Gibbs free energy of the system, ^{[28– 31]} i.e. min(Δ G) = min (Δ H − TΔ S), in which the entropy is considered in our work according to the method in Refs.  [30], [31], [39]–   [42]. This procedure leads to a set of non-linear equations as follows:

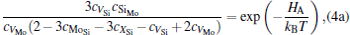
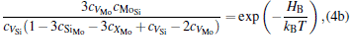
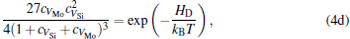
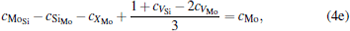
where c_iα is the concentration of species i on a sublattice; k_B is the Boltzmann’ s constant; T is the investigated temperature; c_Mo and c_X are the concentrations of Mo and alloying element X (Al, Cr, W, and Nb), respectively; H_A, H_B, H_C, and H_D are the enthalpy changes of the defect reactions (Eq.  (3)), and can be expressed as the following equations:

Here, H_iα is the formation enthalpy of species i on a sublattice, and listed in Table  1. Because of the influence of the occupation on two different sublattice sites of alloying elements, we find that equation  (4) in this work is more complex than the non-linear equations in Ref.  [28]. The numerical solution of Eq.  (4) predicts the equilibrium concentrations of all types of point defects for a given composition at a given temperature. The fraction of X in the Mo sublattice is defined as c_XMo/(c_XMo + c_XSi), and it can reflect the site preference of the X atom. If c_XMo/(c_XMo + c_XSi) < 1/3, X tends to occupy the Si sublattice; if c_XMo/(c_XMo + c_XSi) > 1/3, X tends to occupy the Mo sublattice; if c_XMo/(c_XMo + c_XSi) = 1/3, X tends to occupy randomly both Mo and Si sublattices.

According to Refs.  [30] and [31], the site preferences of ternary alloying elements in C11_b MoSi₂ at T = 0  K are governed by enthalpy only. The 0  K site occupancy behaviors of substitutional ternary elements in C11_b MoSi₂ can be classified into the following three general types:

(i) H_XMo + H_MoSi − H_XSi < 0: X tends to occupy the Mo sublattice site due to the thermal excitation X_Si + Mo_Mo → X_Mo + Mo_Si.

(ii) H_XMo + H_MoSi − H_XSi > H_MoSi + H_SiMo (or H_XMo − H_XSi − H_SiMo > 0): X tends to occupy the Si sublattice site due to the thermal excitation X_Mo + Si_Si → X_Si + Si_Mo.

(iii) 0 < H_XMo + H_MoSi − H_XSi < H_MoSi + H_SiMo: The site preference of X is composition-dependent. X prefers the Si sublattice sites in Mo-rich and the Mo sublattice sites in Si-rich, and shows no site preference in stoichiometric C11_b MoSi₂ where X randomly occupies both Mo and Si sublattices.

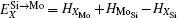
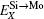
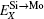
Therefore, using a simple parameter defined as can be sufficient to determine the 0-K site preference nature of any ternary element in C11_b MoSi₂. Essentially, the parameter characterizes the energy cost associated with the transfer of an X atom from an Si site to an Mo site in MoSi₂, in accordance with the reaction:X_Si + Mo_Mo → X_Mo + Mo_Si. Figure  1 shows our first-principles calculated values for ternary elements (Al, Cr, W, and Nb) in C11_b MoSi₂. The formation energy of an antisite defect pair in C11_b MoSi₂, i.e., H_SiMo + H_MoSi, is calculated to be 8.78  eV. This value of would differentiate between the site preference behaviors (type-II and type-III) of X in C11_b MoSi₂. According to Fig.  1, doping MoSi₂ with Al, Cr, W, or Nb shall fall into type-III at 0  K. In other words, the site preferences of these elements are all composition dependent when the temperature effect can be ignored.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Classifications of the 0-K site preference behavior of Al, Cr, W, and Nb in C11b MoSi2 according to the parameter .

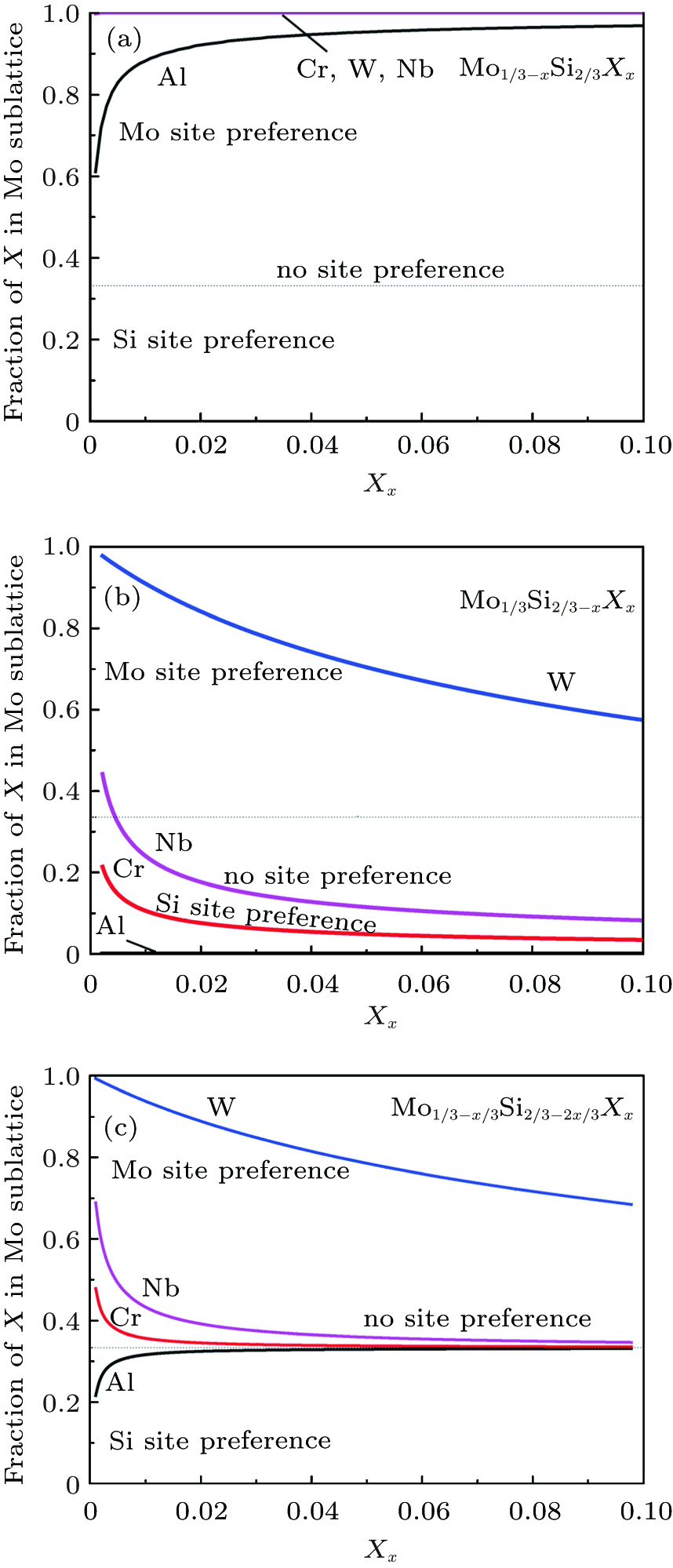
At elevated temperatures, we adopt the statistical– mechanical thermodynamics model in combination with first-principles formation enthalpies to revisit the site preference problem. The site preferences of these ternary elements at elevated temperature are sensitively dependent on the composition of MoSi₂. The equilibrium partitioning of ternary elements between Mo and Si sites is predicted as a function of concentrations at T = 1873  K, and the results for Mo-rich, Si-rich, and stoichiometric C11_b MoSi₂ are compared in Fig.  2. The horizontal dashed lines represent the case of type-III (no site preference), i.e., X atoms can randomly occupy both Mo and Si sites. As seen for Si-rich C11_b MoSi₂ in Fig.  2(a), Cr, W, and Nb all tend to substitute only for the Mo sublattice in MoSi₂. The number fraction of X_Mo (X = Cr, W, and Nb) reaches almost 1 at any concentration of interest. Al also shows strong Mo-site preference in Si-rich MoSi₂, but the initial fraction of Al_Mo is ∼ 0.6 only. Its strong preference becomes more prominent with increasing the Al concentration. These conclusions have been approved by many available studies. Our previous experiments^[13] have proposed the Mo-site preferences of Cr and Nb for Si-rich alloy. Feng et al.^[11] have also shown that the intensity of C40-type (Mo_{1 − x}Cr_x)Si₂ phase diffraction peaks gradually increases with the increase of Cr content of a Si-rich alloy in the mode of self-propagating high-temperature synthesis. Xu et al.^[21] have reported the Mo-site preference of Cr detected by x-ray diffraction in a Si-rich alloy (Cr-alloyed MoSi₂-based nanocomposite coatings). Meanwhile, Yang et al.^[43] and Sharif et al.^[23] have pointed out the Mo-site preference of Nb for Si-rich alloy with 1  at.% (atom percent) Nb and 5  at.% Nb by arc-melting at various high temperatures, respectively.

Fig.  2.

	Figure Option ViewDownloadNew Window
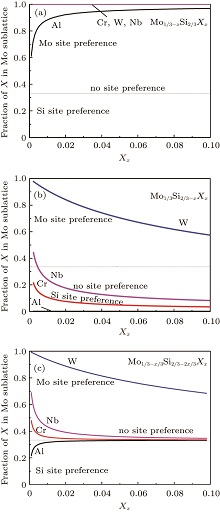	Fig.  2. Predicted fractions of X substitution in the Mo sublattice in (a) Si-rich, (b) Mo-rich, and (c) stoichiometric C11b MoSi2 at 1873  K, as a function of X concentration.

The situation is totally different in Mo-rich MoSi₂ as seen in Fig.  2(b). Al, Cr, and Nb each have a predominant preference for the Si sublattice sites at all concentrations, while W has a strong tendency to substitute Mo. For each element, the Si-site preference increases rapidly with concentration increasing. Yanagihara et al.^[44] have pointed out that Al prefers a Si site for Mo-rich alloy with 10  at.% Al prepared by arc-melting. Hou et al.^[45] have also considered that Mo(Si, Al)₂ increased with increasing the content of Al for each of these Mo-rich alloys (MoSi₂-0, 15.3, 22, and 29.3  at.% Al coatings) prepared by electrothermal explosion ultrahigh speed spraying technology. Moreover, the Si-site preference of Al for Mo-rich alloy has been approved by a number of previous experiments.^{[46– 49]}

The most complicated situation is for the stoichiometric C11_b MoSi₂ (Fig.  2(c)). At almost all concentrations, W has a strong site preference for Mo sublattices. Cr and Nb show a very weak Mo-site preference while Al shows a very weak Si-site preference. As the concentration increases, Cr, Nb, and Al tend to randomly substitute for both Mo and Si sites. Mitra and Rao^[50] have shown that 3.1-at.% Al replaced Si in MoSi₂, forming a solid solution or Mo(Si, Al)₂ in the oxidation of MoSi₂– 9  at.% Al alloy at 1200  ° C. Xu et al.^[51] have also reported the Mo-site preference of W detected by x-ray diffraction in a stoichiometric alloy prepared by a mechanical-assistant combustion synthesis method. The extensive experimental results show that WSi₂ also possesses the C11_b structure and often forms a complete solid solution with MoSi₂, which can indicate the Mo-site preference of W for W-alloyed MoSi₂-based alloys with different stoichiometric ratios.^[52]

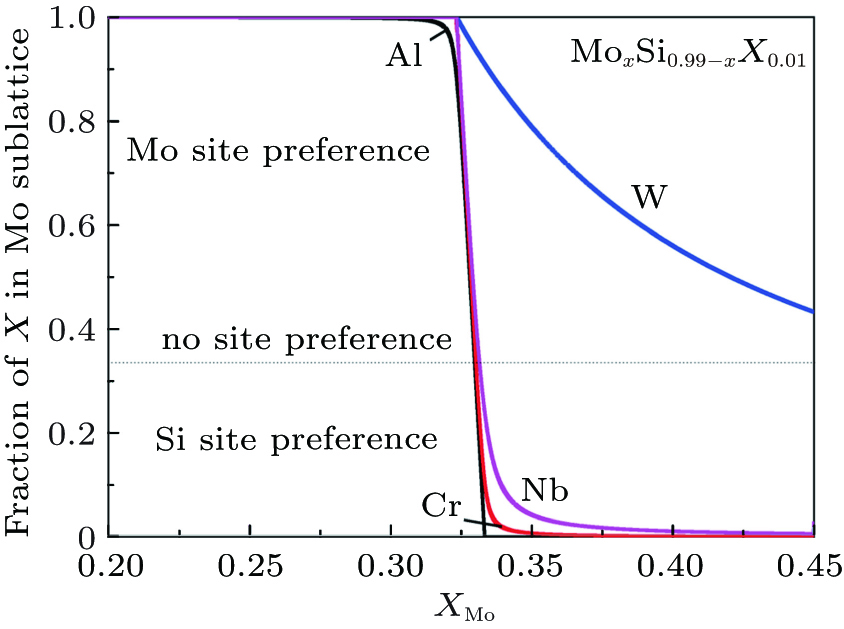
Figure  3 further comparatively shows the site preference of 1  at.% X in C11_b MoSi₂ at 1873  K, as a function of Mo concentration. The doped Mo_xSi_{0.99− x}X_0.01 is Si-rich for x < 1/3, and Mo-rich for x > 1/3. Clearly, at 1873  K, Al, Cr, and Nb can be classified as type-III elements, exhibiting strongly composition-dependent site preference at around x = ∼ 1/3. The site preferences of Al, Cr or Nb change drastically when the compound deviates from its stoichiometric composition. The ternary element partitions into the Mo sublattice in the Si-rich composition range, and into the Si sublattice in the Mo-rich composition range. It is worth noting that W shows a consistent preference for the Mo sublattice over the whole composition range. 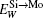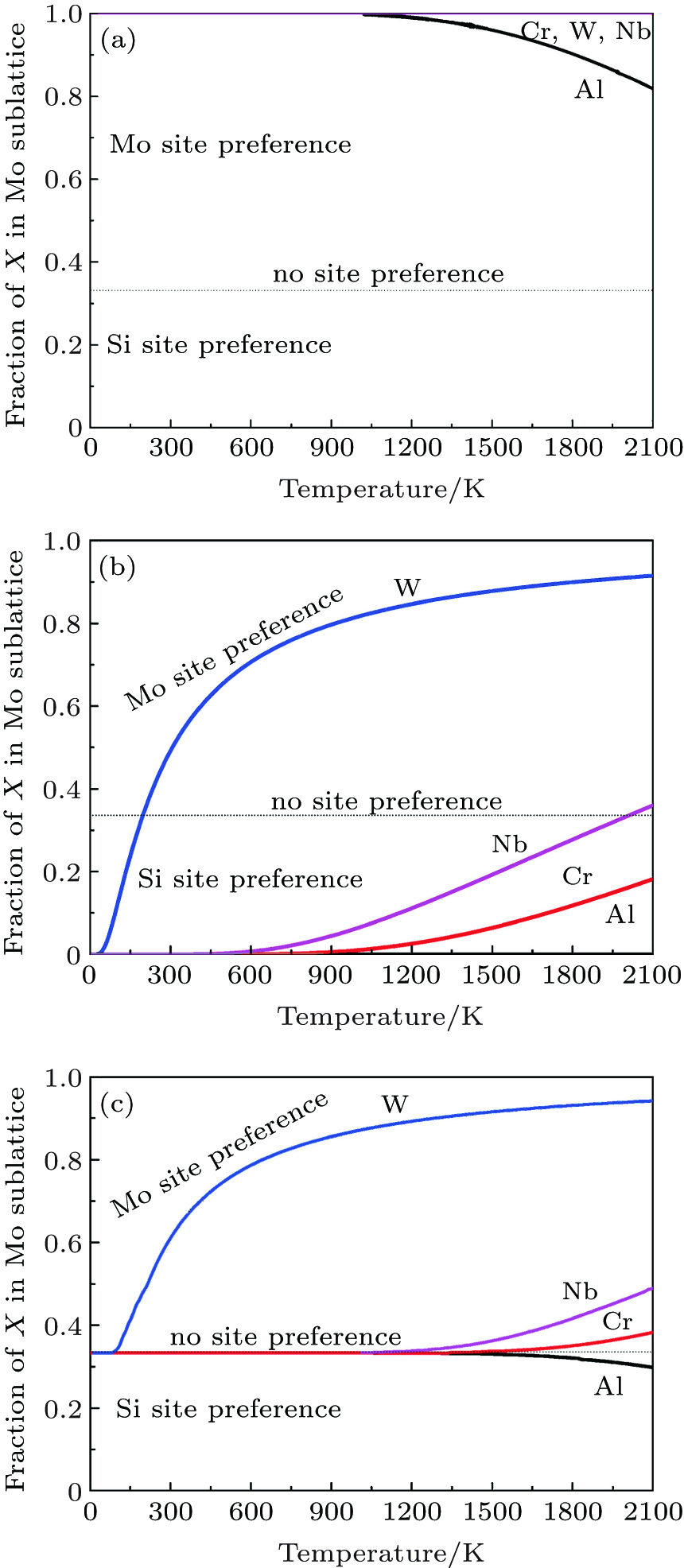Recall that the value of is very small and positive but nearly zero in Fig.  1, thus the site preference of W in MoSi₂ shows very weak composition dependence (i.e., the type-III behavior) at low temperature, but tends to follow the type-II behavior to substitute for Mo sites under the increased entropy effects at elevated temperatures. The conclusion again indicates the Mo-site preferences of W for W-alloyed MoSi₂-based alloys with different stoichiometric ratios, which are in accordance with the previous experimental results.^[52]

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Predicted site preferences of 1% X in MoSi2 as a function of Mo concentration at 1873  K.

To manifest the temperature effect on site preference, we predict the equilibrium partitioning of 1% X between Mo and Si sites in the doped MoSi₂ as a function of temperature in Fig.  4. In Si-rich MoSi₂ (Fig.  4(a)), Al, Cr, W, and Nb each have a predominant preference for the Mo sublattice over the whole temperature range. The fraction of Al in the Mo sublattice starts to decrease rapidly above 1200  K. 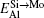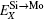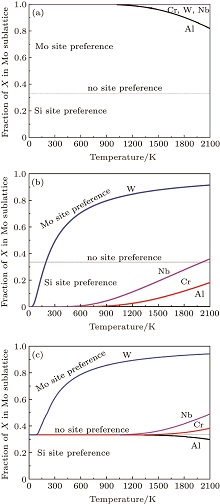This happens because the value of predicted at 0  K is so close to H_SiMo + H_MoSi (see Fig.  1) that the entropy effect at high temperature facilitates the change of the site preference behavior from type-III to type-I. Just a few experimental data are available for the site preferences of ternary elements in MoSi₂ as a function of temperature. Sharif et al.^[23] have also considered the case that Nb atoms occupied the Mo sublattices from 400  ° C to 1600  ° C for Si-rich alloy with 1  at.% Nb by arc-melting. In contrast, in Mo-rich MoSi₂ (Fig.  4(b)), Al has a predominant preference for the Si sublattice over the whole temperature range. The partition of Cr, W, and Nb to the Mo sublattice is strongly dependent on temperature. Cr, W, and Nb each show a preference for the Si sublattice at low temperatures, but start to choose Mo sites as temperature increases. In particular, the fractions of W and Nb in the Mo sublattice increase to such an extent that their preferences are reversed. The increase of the extent of X fractions in the Mo sublattice with increasing temperature follows the same ordering of values as seen in Fig.  1. Zhang et al.^[53] have proposed that Al atoms occupied the Si sublattices determined by x-ray diffraction for Mo-rich alloy with 1  at.% Al prepared by direct current hot pressing from 1300  ° C to 1700  ° C. Dasgupta and Umarji^[19] have considered the fact that Nb prefers the Mo site and Al prefers the Si site for a MoSi₂-based with 1  at.% Nb ((Mo_0.97Nb_0.03)(Si_0.96Al_0.04)₂) prepared by arc-melting at 1800  K. Finally, in stoichiometric MoSi₂ (Fig.  4(c)), all elements are partitioned randomly between Mo and Si sites at low temperatures. As the temperature increases, Cr, Nb, and W each show a preference for the Mo sublattice, while Al for the Si sublattice. In conclusion, the site preference behaviors show strong dependence on both composition and temperature at elevated temperature. Our conclusion is in good agreement with the available experimental data, and more experimental data are demanded in order to verify our proposed cause.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Predicted site preferences of X in (a) Si-rich Mo0.3233Si0.6667X0.01, (b) Mo-rich Mo0.3333Si0.6567X0.01, and (c) stoichiometric Mo0.33Si0.66X0.01, at different temperatures.

Site occupancy of alloying elements is related to the mechanical properties of MoSi₂. It is reported that the additions of alloying elements in MoSi₂ can improve the fracture toughness at room temperature, which is attributed to alloying elements weakening the Mo– Si bonds and introducing more metallic nature to the bonding.^[54] The effects of these alloying substitutions on the service performance of MoSi₂ are desired to be developed in future work.

The site occupation behaviors of ternary elements (X = Al, Cr, W, and Nb) in C11_b MoSi₂ are investigated as a function of composition and temperature by using first-principles calculations with the statistical mechanical thermodynamics model. A simple parameter defined as 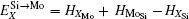can be used for roughly estimating the nature of the site preference at high temperature. Our calculations manifest the strong composition and temperature dependence of the site occupation behaviors of these ternary elements in C11_b MoSi₂. Some calculated results have been verified in previous experiments.