†Corresponding author. E-mail: jianweishuai@xmu.edu.cn
*Project supported by the National Natural Science Foundation for Distinguished Young Scholars of China (Grant No. 11125419), the National Natural Science Foundation of China (Grant No. 10925525), and the Funds for the Leading Talents of Fujian Province, China.
The Langevin approach has been applied to model the random open and closing dynamics of ion channels. It has long been known that the gate-based Langevin approach is not sufficiently accurate to reproduce the statistics of stochastic channel dynamics in Hodgkin–Huxley neurons. Here, we introduce a modified gate-based Langevin approach with rescaled noise strength to simulate stochastic channel dynamics. The rescaled independent gate and identical gate Langevin approaches improve the statistical results for the mean membrane voltage, inter-spike interval, and spike amplitude.
In recent years, there has been increasing interest in the simulation of stochastic channel dynamics, i.e., the random opening and closing of ion channels. The stochastic Hodgkin– Huxley (HH) neuron[1] can be accurately simulated with the Markov method or Gillespie method.[2– 5] However, the computational cost of these Markov-based methods becomes very high with an increase in the number of channels. Thus, various Langevin approaches have been suggested wherein the channel variables are modulated by Gaussian noise.[6– 11]
Among these approaches, Fox and Lu suggested a simple gate-based Langevin approach for a stochastic HH model.[6] With such an approach, the stochastic dynamics of Na+ and K+ channels, consisting of several gates to control the channel opening and closing, can be calculated with the gate open fractions disturbed by Gaussian noise. The noise strength is determined by the channel number and fraction of open gates. Because of its simplicity, such a gate-based Langevin approach has been applied extensively to simulate stochastic HH channel dynamics and other channel systems.[12– 15]
However, in the past few years, increasing evidence has indicated apparent inaccuracies in gate-based Langevin approaches.[16– 19] Mino et al.[16] first reported that the firing efficiency and spiking latency of the Fox– Lu gate-based approach for a neuron with 1000 Na+ channels responding to a pulse current differed from those for the Markov method. They suggested that, because the generation of action potentials in the HH model is highly dependent on the number of open Na+ channels, the number of open channels in the approach should be rounded down to the nearest integer to obtain better statistical results. Later, Bruce[17] argued that a better treatment would be to round up the number of open Na+ channels to its nearest integer. Compared to rounding to the nearest integer, the rounding-down method always underestimates the Na+ current. Thus, statistically, the rounding-down treatment may produce decreased firing efficiency and increased spike latency.
Because each channel consists of several gates, Shuai and Jung[18] suggested two different considerations for the gate-based approach. In detail, each K+ channel has 4 n-gates and each Na+ channel has an h-gate and 3 m-gates.[1] For the same type of gate, the gates can be either identical (and thus be disturbed by identical Gaussian noise) or independent (and thus be disturbed by different Gaussian noises). Later, Goldwyn et al.[8] pointed out that although the consideration of independent gates is more biologically realistic, the identical gate approach derives better statistics for action potentials than the independent gate approach for the stochastic HH neuronal model. However, Sengupta et al.[7] showed that the identical gate approach still underestimates the channel noise, resulting in overestimation of information rates with 6000 Na+ and 1800 K+ channels.
Huang et al.[19] proposed the rescaled gate-based approach to address the localized intracellular Ca2+ signals (Ca2+ puffs) that are released from a cluster of Ca2+ channels in the ER membrane. It has been shown that, by properly introducing a factor to rescale the gate noise strength, the modified Langevin approach can better simulate stochastic calcium channel dynamics. Compared to the Ca2+ channels in ER membrane where only one type of gate is discussed with stochastic dynamics, the Na+ and K+ channels in the HH neuron present a more complicated situation because there are three different types of gates (i.e., 4 n-gates, 1 h-gate, and 3 m-gates). Thus, it is interesting to consider whether the gate noise can be rescaled to improve the gate-based Langevin approach for stochastic HH neuronal dynamics. In this study, we compare the identical gate Langevin approach and independent gate Langevin approach with rescaled-strength of Gaussian noise for the stochastic HH neuronal model. We show that the rescaled Langevin approach can greatly improve the statistical results.
The neuron membrane voltage for the deterministic HH model is given by the following equation[1]

with V representing the membrane potential and C representing the membrane capacitance. The currents of Na+ channels and K+ channels and the leakage are given by INa = gNahm3(V − ENa), IK = gKn4(V − EK), and IL = gL(V − EL), respectively. The equation for the gating variable x (with n for K+ channels and m and h for Na+ channels) is

All of the model parameters have been described previously.[1, 11] The open/close two-state Markov process for each single gate (n, m, and h gates) has also been previously described[4, 11] and is considered to be a standard Markov method for stochastic channel dynamics in the paper.
There are two ways to consider the Gaussian noise for the gate variables. The first one is to assume identical gate dynamics with noise:[6, 8, 18]

where ζ (t) is the uncorrelated Gaussian white noise with zero mean and unit variance, and Nx represents the number of corresponding Na+ or K+ channels. The term G is a time-dependent noise strength with

The second way is to assume the independent gate dynamics for each gate. As a result, the channel currents are rewritten as INa = gNahm1m2m3(V − ENa) and IK = gKn1n2n3n4(V − EK), with
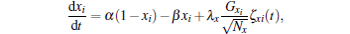
where xi represents h, m1, m2, m3, n1, n2, n3, and n4. In the simulation, we keep the boundary limitation of 0 ≤ x ≤ 1 by simply requiring x = 0 or 1 once it is out of [0, 1].
In the original Fox– Li Langevin approach, λ x = 1 (i.e., λ h = λ m = λ n = 1).[6] However, we introduce the rescale factor λ x to better simulate the strength of Gaussian noise on gate dynamics in the Langevin approach. We suggest that a set of rescale factors {λ x} can be optimally selected to produce better statistical results for action potentials of a stochastic HH neuron.
Here, we use the number N to denote the number of K+ channels. We also assume that the density of Na+ channels is always three times higher than that of K+ channels.[4, 6] Thus, N potassium channels are equivalent to 3N sodium channels in the model. We do not consider any current stimulus on the model, thereby deterministically obtaining a stable fixed point for the model.
With the two-state Markov method, the stochastic action potentials can be obtained. Then, the mean voltage and its standard deviation, the mean inter-spike interval, and the mean spike amplitude are calculated as a function of channel number N from 10 to 2000. In our simulation, the first goal is to find an optimal set of λ n, λ m, and λ h by comparing the error of the action potential statistics between the Langevin approach and the standard Markov HH model.
For the identical gate approach, our numerical simulations indicate that the statistical results for an action potential are insensitive to the change in the factor λ h in the range of 0.5 to 3.0. This is understandable because the h-gate is a slow inactivation variable for Na+ channels to terminate the Na+ current. This variable has little effect on the initiation of action potentials, and the termination of the action potential is mainly determined by the K+ current. Therefore, we set λ h = 1.0. Furthermore, the simulations show that the two optimized factors λ n = 2.0 and λ m = 1.8 provide satisfactory mean voltages and mean inter-spike intervals.
For the independent gate approach, our simulation suggests that the statistical results for the action potential are insensitive to not only the change in λ h, but also the change in λ m. This observation indicates that, for the independent gate approach, the strength of Gaussian noise added on the Na+ channels has little effect on stochastic activity. Therefore, we set λ h = λ m = 1.0. Furthermore, our simulation shows that the independent gate approach with λ n = 3.0 can produce satisfactory statistical results.
In the following subsection, we compare the statistical results for action potentials obtained by the Markov method (Markov) and different Langevin approaches, including the original independent gate approach (Indep), original identical gate approach (Ident), rescaled independent gate approach (rescaled Indep), and rescaled identical gate approach (rescaled Ident).
The stochastic channel noise will produce a fluctuation of membrane voltage. We first compare the mean, 〈 V〉 , and standard deviation, DV, of the voltage obtained with these methods. The mean and standard deviation of the voltage are plotted in Fig. 1 against the channel number N.
Both the original identical and independent gate approaches typically produce a smaller value for the mean voltage than the Markov method. As a result, the rescale factor λ ≥ 1 has to be considered to produce larger Gaussian noise in order to obtain a higher membrane voltage. The rescaled identical gate approach can reproduce a higher mean membrane voltage than the rescaled independent approach.
A maximal and a minimal voltage are detected during each time window of 0.1 sec, in which several action potentials will typically be observed. Then, the averaged maximal and minimal voltages can be calculated for long-term recording. The resulting averaged maximal and minimal voltages are plotted in Fig. 2 against channel number N. The original independent gate approach shows worse curves for both the averaged maximal and minimal voltages at N > 100. The rescaled independent gate approach gives curves closest to those obtained by the Markov method.
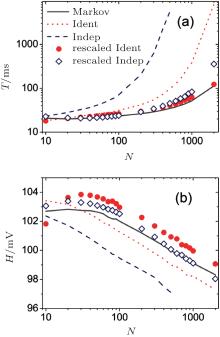
Next, we study the mean inter-spike interval (T) and the mean spike amplitude (H), which are shown in Fig. 3 as a function of channel number N. With increasing N, the channel noise becomes small, generating an increasing mean inter-spike interval and a decreasing mean spike amplitude. Because the Gaussian noise given by the original identical and independent gate approaches is small, these two approaches produce a larger mean interval and smaller amplitude than those obtained by the Markov method for N > 30. Better results are generated with the larger noise strength for the two rescaled approaches. The rescaled identical gate approach produces more accurate mean inter-spike intervals, whereas the rescaled independent gate approach provides more accurate spike amplitudes.
Now we discuss why the rescaled approaches achieve better statistical results. Deterministically, without any channel noise, a stable fixed point is obtained for the HH neuron model, given a zero open fraction for Na+ channels and a small fixed open fraction for K+ channels. When considering the stochastic channel dynamics, the random opening and closing of channels cause fluctuation in the open fractions of K+ and Na+ channels in the ranges of [0, 0.35) and [0, 0.25), respectively.
For a proper Gaussian noise added on the gate variable, the probability to drive the channel open fraction to zero (i.e., the channel open fractions n1n2n3n4 = 0 and m1m2m3h = 0) should be similar to that given by the Markov method. Therefore, we study the probabilities P(n1n2n3n4 = 0) and P(m1m2m3h = 0) that all the K+ and Na+ channels are in the closing state. Figure 4 compares the plots of the probabilities P(n1n2n3n4 = 0) and P(m1m2m3h = 0) against N from 10 to 2000 for the Markov method and 4 different Langevin approaches. For the original identical and independent gate approaches, the Gaussian noises are too small, resulting in low probability at the zero open fraction.
 | Fig. 4. Closing probability of ion channels. The probabilities (a) P(n1n2n3n4 = 0) and (b) P(m1m2m3h = 0) that all K+ and Na+ channels are closed against N. |
However, for the two rescaled approaches, the rescaled Gaussian noise that is added on the gate variables is actually slightly larger, and such Langevin approaches can generate a strong fluctuation for gate variables. The strong fluctuation of gate variables results in larger probability at the zero open fraction, which is more similar to the probability given by the Markov method. With a better approximation of the open fractions for K+ and Na+ channels, the rescaled Langevin approaches can achieve better statistical results for fluctuated membrane voltage.
Gate-based Langevin approaches have been widely applied for the study of stochastic channel dynamics after Fox and Lu proposed such approaches to simulate the stochastic HH neuronal model in 1994.[6] It has been realized that these simple approaches actually suggest an over-simplified noise approximation for stochastic channel simulation, leading to qualitatively correct but quantitatively incorrect conclusions. Thus, an interesting question is how to construct an improved Langevin approach to better approximate the Markovian channel dynamics.
In this paper, we indicate that the Gaussian noise suggested by the original identical and independent gate approaches is typically small. Thus, we propose to rescale the strength of the Gaussian noise for the gate-based Langevin approaches for the stochastic HH neuron model. With a larger Gaussian noise, the rescaled Langevin approaches can generate a strong fluctuation for gate variables, resulting in a larger probability at the zero open fraction, as given by the Markov method. With a better approximation of open fractions for K+ and Na+ channels, the rescaled Langevin approaches can achieve better statistical results for fluctuating membrane voltage. Our simulation results show that the rescaled identical gate approach agrees better with the Markov method regarding the calculation of mean membrane voltage and mean inter-spike interval, whereas the rescaled independent gate approach agrees better with the Markov method for the calculation of the bifurcation diagram of the averaged maximal and minimal voltages and the mean spike amplitude.
Because the rescale parameters for Langevin noise are not universal, the rescaled Langevin approach is an ad-hoc approach that calls for preliminary simulations to determine the empirical scaling factors. Stochastic channel dynamics are found widely in neuron dynamics and intracellular calcium signaling systems.[15] Considering the simplicity of the gate-based Langevin approach, we believe that the rescaled Langevin approach may be applicable in many stochastic channel systems.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|