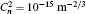†Corresponding author. E-mail: zhaosm@njupt.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61271238 and 61475075), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20123223110003), the Natural Science Research Foundation for Universities of Jiangsu Province of China (Grant No. 11KJA510002), the Open Research Fund of Key Laboratory of Broadband Wireless Communication and Sensor Network Technology, Ministry of Education, China (Grant No. NYKL2015011), and the Innovation Program of Graduate Education of Jiangsu Province, China (Grant No. KYLX0810). Gong Long-Yan is partially supported by Qinglan Project of Jiangsu Province, China.
In this paper, we propose a measurement-device-independent quantum-key-distribution (MDI-QKD) protocol using orbital angular momentum (OAM) in free space links, named the OAM-MDI-QKD protocol. In the proposed protocol, the OAM states of photons, instead of polarization states, are used as the information carriers to avoid the reference frame alignment, the decoy-state is adopted to overcome the security loophole caused by the weak coherent pulse source, and the high efficient OAM-sorter is adopted as the measurement tool for Charlie to obtain the output OAM state. Here, Charlie may be an untrusted third party. The results show that the authorized users, Alice and Bob, could distill a secret key with Charlie’s successful measurements, and the key generation performance is slightly better than that of the polarization-based MDI-QKD protocol in the two-dimensional OAM cases. Simultaneously, Alice and Bob can reduce the number of flipping the bits in the secure key distillation. It is indicated that a higher key generation rate performance could be obtained by a high dimensional OAM-MDI-QKD protocol because of the unlimited degree of freedom on OAM states. Moreover, the results show that the key generation rate and the transmission distance will decrease as the growth of the strength of atmospheric turbulence (AT) and the link attenuation. In addition, the decoy states used in the proposed protocol can get a considerable good performance without the need for an ideal source.
Quantum key distribution (QKD)[1] enables two remote users to securely exchange cryptographic keys in the presence of an eavesdropper, and it has received a great deal of attention[2– 7] since Bennett and Brassard proposed the first QKD protocol (BB84) in 1984.[1] Theoretically, it is unconditionally secure.[8, 9] However, in a practical QKD system, an eavesdropper (Eve) might successfully eavesdrop some information of the key by utilizing the defects of measurement devices.[10– 13] Recently, a measurement device independent quantum key distribution (MDI-QKD) protocol has been proposed to make the BB84 protocol free from any possible side-channels in detectors.[6] In the MDI-QKD protocol, neither Alice nor Bob performs any measurements, but an untrusted third party, called Charlie, detects photons. Alice and Bob distill a secret key according to Charlie’ s measurement results. It is shown that MDI-QKD protocol is free from side-channels because Alice and Bob do not employ photon detectors in the protocol. The MDI-QKD protocol has been extensively studied both experimentally[14– 18] and theoretically[19– 27] since it was proposed.
Most of the MDI-QKD protocols rely on either the polarization[6] or phase[18, 19] of faint laser pulses as information carriers, and the use of polarization encoding limits the degree of a photon to encode information. Unlike the limited degree of freedom on polarization or phase states, orbital angular momentum (OAM) states have attracted a great deal of attention since there are infinite OAM eigenstates in a single-photon. Furthermore, OAM states are invariant under rotations about the propagation direction, which makes the sender and receiver to avoid the reference frame alignment.[28, 29] These outstanding properties make OAM states that have been used in the BB84-type QKD protocol in free-space links.[30– 32] However, the MDI-QKD with OAM states as information-carriers has been so far much less analyzed and reported.
In this paper, we propose an MDI-QKD protocol using OAM in the free-space link, named the OAM-MDI-QKD protocol. In the protocol, OAM states of photons are used as the information carriers. The decoy-state method[7] is adopted to overcome the security loophole caused by the weak coherent pulse source, together with a high efficient OAM sorter[33, 34] that is employed to differentiate the different OAM states. Since OAM describes the spatial distributions of wave-functions with helical phases, [35] the OAM-MDI-QKD protocol is inevitably sensitive to atmospheric turbulence (AT) interference.[36– 39] The performance of the proposed protocol under atmospheric turbulence and link attenuation is further discussed.
The organization of the paper is arranged as follows. In Section 2, the decoy-state MDI-QKD protocol using orbital angular momentum states is presented. In Section 3, the key generation rate of the proposed protocol is analyzed, in conjunction with the influence on the performance by both AT and link attenuation in the free-space communications. Here, the general formulas for the contribution of single-photon pulses (gain 

Figure 1 shows the schematic diagram of the proposed OAM-MDI-QKD protocol. Both Alice and Bob produce a laser beam and modulate the photons to be the desired OAM states by illuminating the beam to a spatial light modulator (SLM) with a special hologram. Alice and Bob then obtain phase-randomized weak coherent states, including the decoy states and the signal state by using attenuators. Here, the intensity of the signal state for Alice and Bob is expressed as μ and ν , respectively. Assume both Alice and Bob could use infinite decoy states in the protocol. At a later moment, Alice and Bob send their pulses carrying OAM states to Charlie through a free-space communications link, which is disturbed by AT and link attenuation. In the protocol, Charlie is the only one who operates measurements. The measurement device comprises a beam-splitter (BS), two OAM-sorters and four single photon detectors. After Charlie’ s measurements, Alice and Bob could distill a secret key based on Charlie’ s successful measurement results.
An OAM state is associated with the azimuthal phase of a beam. It could be given as, [39]
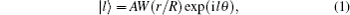
where A denotes an amplitude of the beam, r and θ are the radial and azimuthal coordinates respectively, l is an OAM topological charge and it is an integer, and W(r/R) is an aperture function with radius R. W(r/R) can be expressed as,
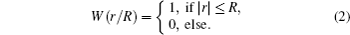
It is shown that the OAM states do not need to align the shared reference frames as long as the z axis is synchronized in the QKD system since the spatial profile of the OAM states is rotational invariance.[28, 29]
For simplification and generality, a two-dimensional OAM-MDI-QKD protocol is discussed. One of the two two-dimensional OAM mutually unbiased bases for the proposed protocol could be defined as
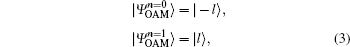
where n represents the encoding bit, which can be taken an integer index from the set {0, 1}. It is named OAM basis. The two states in OAM basis are orthogonal and rotational-invariant. The property of the rotational invariance enables quantum communication without alignment of shared reference frames and decreases the errors due to misalignment of shared reference frames.
Meanwhile, the other basis, called the superposition basis (SUP basis) is defined as
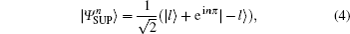
where n is the encoding bit (0 or 1). The states in the SUP basis are a superposition of the | l〉 state and the | − l〉 state, and the two states in the SUP basis are orthogonal too. However, the two states in the SUP basis do not have the property of the rotational invariance, thus alignment of shared reference frames is necessary.
Charlie is the only one who could operate measurements. His measurement device is composed of a beam-splitter (BS), two OAM-sorters, and four single photon detectors. When both the photons carrying OAM states arrive at the 50:50 BS, a Hong– Ou– Mandel (HOM) effect takes place.[40] Assume that the photon with the OAM state 

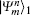



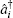



where

and

It is indicated that | Σ − 〉 will disappear if both Alice and Bob send the same photon states and choose the SUP basis (namely 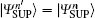
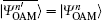
Moreover, high efficient OAM-sorters[33, 34] are adopted to differentiate the different OAM states. For OAM basis states, they are converted to the different truncated plane waves with wavefront tilts which are proportional to the OAM charge l. For SUP basis states, they are transformed to two different truncated plane waves. In fact, the OAM-sorter has two static special optical transformations (unwrapper (R1) and phase corrector (R2) in Fig. 1) to map the azimuthal phase profile of an OAM mode to a tilted planar wavefront, and the plane waves are then separated and focused to specified lateral positions by a lens. The sorting is exclusively based on unitary transformations and in theory can achieve a power transmission efficiency of unity.
Four single photon detectors (L0, L1 or R0, R1) are placed in the focal planes of the lenses to detect two OAM states simultaneously (L0 or R0 for the OAM state | l〉 , while R1 or L1 for the OAM state | − l〉 ). Assume that if and only if two of Charlie’ s four detectors are triggered at the same time (triggers both at L0 and L1, at R0 and R1, at L0 and R0, and at L1 and R1), Charlie gets a successful measurement result. After Charlie announces his measurement results, Alice and Bob tell each other what basis she or he chooses, and only keep the results with the same basis. Table 1 shows a probability distribution of the successful measurements for Charlie when both Alice and Bob choose the same basis. The results show that when Alice and Bob choose the SUP basis and Charlie announces that both L0 and R0, or both R1 and L1 are triggered at the same time, Alice and Bob have opposite bits; otherwise, Alice and Bob have the same bit. On the other hand, when Alice and Bob choose the OAM basis and Charlie announces a successful measurement, Alice and Bob have the same bit. Therefore, if Alice and Bob use the results with the OAM basis as the key bits and simultaneously use the results with the SUP basis as the testing bits, Alice and Bob can share a secret key after error correction and privacy amplification procedures.
| Table 1. A probability distribution for Charlie’ s successful measurements when both Alice and Bob choose the same basis. |
Correspondingly, the proposed protocol has some advantages. Firstly, the proposed protocol uses OAM states to carry information. It paves a way to exploit a high-dimensional MDI-QKD protocol for transmitting more than one bit per photon, so as to greatly enhance the key generation rate performance. Secondly, the property of the rotational invariance of the states in OAM basis has enabled quantum communication without alignment of shared reference frames and decreases the errors due to misalignment of shared reference frames, which slightly improves the performance and further simplifies the practical system. In addition, Alice and Bob can reduce the number of flipping bits in the secure key distillation.
The details of the proposed OAM-MDI-QKD protocol are listed below.
Step 1 Alice and Bob randomly choose a basis (OAM basis or SUP basis) and a bit (n = {0, 1}). Then they display the corresponding hologram on their SLMs to convert a Gaussian beam to the desired OAM state beam. Subsequently, Alice and Bob randomly produce the signal states and the decoy states by attenuating the beam into various intensities. Then, Alice and Bob send the pulses carrying OAM states to Charlie through a free-space turbulent channel.
Step 2 Charlie receives the pulses and carries out OAM states measurements. If and only if two of the four detectors (L0, L1, R0, and R1) are triggered at the same time, i.e., the same click at L0 and L1, R0 and R1, L0 and R0, and L1 and R1, Charlie gets a successful measurement. Then Charlie announces his measurement results to Alice and Bob.
Step 3 Alice and Bob tell each other what basis she or he chooses, and only keep those results with the same basis corresponding to Charlie’ s successful measurements.
Step 4 Alice and Bob use the results with OAM basis as the key bits and the results with the SUP basis as the testing bits, and then they testify the security of the key distribution.
Step 5 If Alice and Bob make sure the key distribution is secure, they can obtain a raw key. After error correction and privacy amplification, they can distill a secure key.
The key generation rate for the proposed scheme can be written as follows according to the concepts in Ref. [6]
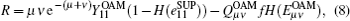
where 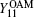
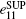


Unfortunately, the purity of OAM states is sensitive to AT and link attenuation, [36– 38] and the key generation rate will be influenced by AT and link attenuation. Usually, the transmission probability η 0, which illustrates the probability of the received photon with the same OAM state as the input, and the transmission probability 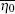
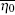


where D is the diameter of the receiver aperture, α is the coefficient caused by the atmospheric absorption and scattering loss (link attenuations), and r0 is the Fried parameter (atmosphere turbulence), [41] which can be further described as,
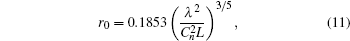
where 
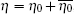

To obtain the key generation rate, the gain 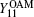
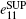

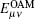

Without loss of generality, the case where both Alice and Bob send a single photon carrying | − l〉 is analyzed, which means that both Alice and Bob choose the same encoding bit n = 0. The joint states after BS are
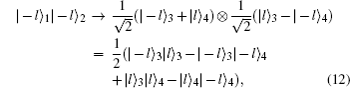
where the subscript i = {1, 2, 3, 4} represents the ith arm of BS. If Charlie receives a vacuum state from Alice (or Bob) because of the losses in the aberration links, the joint states are changed to

Hence, the gain for two of four of Charlie’ s detectors (L0, L1, R0, and R1) triggered at the same time when both Alice and Bob choose n = 0 is

where 
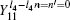
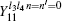

Similarly, the gains when both Alice and Bob choose n = 1, and Alice and Bob choose different encoding bits (n − n′ = ± 1) could be expressed as

and

Therefore, the gain of single-photon pulses in the OAM basis for two of four of Charlie’ s detectors triggered at the same time is
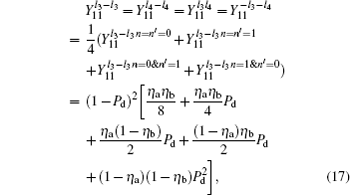
and the gain 
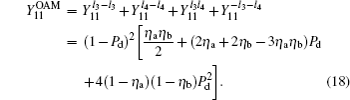
Likely, the gain 

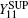


where 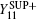

On the other hand, errors are induced by misalignment and crosstalk between states in the SUP basis when Alice and Bob choose different encoding bits while L0 and L1 (or R1 and R0) are triggered simultaneously, or when Alice and Bob choose the same encoding bit while R0 and L0 (or R1 and L1) are triggered simultaneously. According to the crosstalk between different states induced by AT, Charlie receives the different states with the probability t+ = (ta(1 − tb) + (1 − ta)tb)(1 − ed) + ((1 − ta)(1 − tb) + tatb)ed and the same states with the probability t− = (ta(1 − tb) + (1 − ta)tb)ed + ((1 − ta)(1 − tb) + tatb)(1 − ed). So the 

where ta and tb are the crosstalk probability for the states sent by Alice and Bob to Charlie, respectively, and ed represents the misalignment-error probability.
The total gain 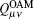

where θ a and θ b are randomized phases. After the pulses pass through two lossy channels between Alice or Bob and Charlie with transmission probability η a and η b, the joint state can then be written as

Then, two cases should be considered. One is both Alice and Bob choose the same encoding bit (n − n′ = 0) and the other case is they choose different encoding bits (n − n′ = ± 1). Let us consider the gain 
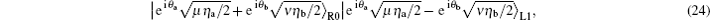
then the detection probabilities of the single-photon detector R0 and L1 should be
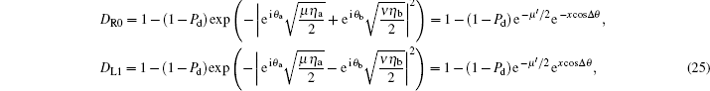
where Pd is the background count rate per detector, 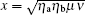

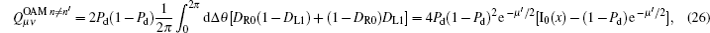
where I0(x) is the modified Bessel function of the first kind.
Similarly, the gain 
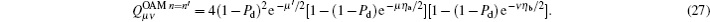
Due to equal probability, the 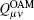

Because the rotational invariance of OAM states enables quantum communication without alignment of shared reference frames, the 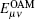
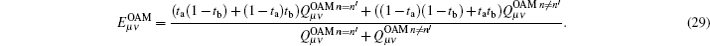
In this section, we will discuss the unconditional security proof of the proposed protocol, which is determined by the EPR-based QKD protocol[7] and the decoy state method.[42] In the protocol, both Alice and Bob use the decoy state method, resulting in the protocol that can avoid a photon number splitting attack.[43] Moreover, Alice and Bob could obtain that gain and QBER when the photons sent to Charlie are single photons. On the other hand, with the help of the virtual qubit idea proposed in Ref. [44], the OAM photon sent from Alice (Bob) to Charlie could be considered as the one real photon of a virtual entangled OAM photons pair, where the virtual OAM photon is kept by Alice (Bob). According to the principles of quantum swapping, [45] the virtual photons kept by Alice and Bob are entangled after Charlie finishes his Bell measurements and announcements. At this time, Alice and Bob are sharing virtual Bell-entangled OAM photons. Therefore, a secure key could be generated by performing the measurements on the virtual Bell-entangled OAM photons. It is indicated that the security of the proposed protocol is equivalent to that of the EPR-based QKD protocol. It has been shown that there is an unconditional security analysis for the EPR-based QKD protocol.[8] Hence, our proposed protocol is an unconditional secure protocol.
In this section, we discuss the performance of the proposed protocol by numerical simulations. The parameters for the numerical simulation are the following. The background count rate for the detector Pd is 3 × 10− 6. The misalignment-error probability in the SUP basis ed is 1.5%. The error correction efficiency f is 1.16. The OAM charge l is 10. The diameter of the receiver aperture D is 15cm and the wavelength λ is 1550 nm. Assume that the distance between Alice and Charlie is equivalent to the distance between Bob and Charlie (La = Lb), the transmission probability from Alice to Charlie is the same as that of Bob to Charlie (η a = η b), and the crosstalk probability of Alice (ta) is equal to that of Bob (tb), where 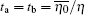
Figure 2 shows the key generation rate performance of the OAM-MDI-QKD protocol against the transmission distance, in comparison with that of the polarization-based MDI-QKD protocol with the same experimental parameters. The results show that the key generation rate performance of the proposed protocol is slightly better than that of the polarization-based MDI-QKD protocol, because Alice and Bob need not align their reference frames when both Alice and Bob use the OAM basis in the proposed protocol, which results in a lower error rate 
In order to demonstrate the key generation rate performance influenced by AT and link attenuation, figure 3 illustrates the key generation rate against the transmission distance with different strength of AT 

In order to display the benefits of using decoy states, figure 4 shows the key generation rate of the proposed protocol using the weak coherent states without decoy states, the weak coherent states with the infinite decoy states, and the perfect single photon source. Figure 4(a) is the performance as a function of the strength of AT 
We have proposed a decoy-state MDI-QKD protocol using orbital angular momentum states in this paper. In the protocol, the mutually unbiased bases of OAM states are prepared, and the modes of different OAM states in the MUBs are represented for different information. In order to overcome the security loophole caused by the weak coherent pulse source, the decoy states are used. A highly efficient OAM-sorter is adopted in the measurement device to obtain the output OAM state. We analyzed the key generation rate performance of the proposed protocol through a free-space atmospheric turbulent link, and discussed the performance by numerical simulations. The results show that the protocol has a slightly improved performance in comparison with that of the polarization-based MDI-QKD protocol with the same experimental condition. Moreover, the MDI-QKD protocol based on OAM states with higher dimensions could further enhance the key generation rate performance. In addition, AT and link attenuation have influenced on the key generation rate performance and the transmission distance. The stronger AT and higher link attenuation make the key generation rate performance drop quickly, and the transmission distance decreases straightway. Finally, the results demonstrate that the proposed protocol with the decoy states could get a considerably good performance without the need of an ideal source.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|