†Corresponding author. E-mail: mazharaliawan@yahoo.com
We study decoherence effects on genuine multipartite entanglement for three and four qubits, spatially separated and subjected to local Lorentzian reservoirs. Employing recent techniques to compute genuine negativity for multipartite systems and an exact solvable model, we analyze the dynamics of genuine entanglement for different coupling bandwidths and detunings. We find that collapses and revivals can occur by varying these parameters for various multipartite quantum states.
Quantum entanglement is essential for several practical applications in the emerging field of quantum information. This feature inspires us to develop a theory of entanglement and several methods to partially avoid the unalterable process of decoherence.[1, 2] As we desire to be able to generate and manipulate entanglement in experiments, therefore it is essential to study the effects of various environments on entanglement.[3] This problem has received considerable attention for bipartite and multipartite systems.[4– 33] Some authors have studied only bipartite aspects of entanglement of multipartite states, [14– 16] nevertheless these studies can capture only partial information because genuine entanglement is more distinct in nature than the entanglement among various partitions. Unless there is an adequate theory of multipartite entanglement, one can talk about lower bounds of entanglement instead of its exact value.[17] The precise expression of multipartite entanglement was only computed for a particular type of decoherence and definite quantum states.[19] In addition, in order to better judge the dynamical behavior of a state, we need to compare its dynamics with the dynamics of random states. In our previous studies, we concentrated on the dynamics of multipartite states by investigating a computable measure of genuine multipartite entanglement for several decoherence models.[34– 38]
In this work, we extend our study to the dynamics of genuine entanglement under a specific type of non-Markovian noise. Although, the approximation of weak interaction and no back action of environment on the principal system might be valid for certain circumstances, however in reality most systems are non-Markovian. It is important to simulate the effects of non-Markovian environments on genuine entanglement. There are already some studies on the dynamics of entanglement under non-Markovian reservoirs in both theories and experiments.[39– 42] We will adopt a model through which the environment coupling can be tuned across the Markovian and the non-Markovian regimes. We will then examine the entanglement evolution of the qubits for different classes of initial states. Recent progress in the theory of multipartite entanglement has enabled us to study decoherence effects on actual multipartite entanglement and not on entanglement among bipartitions. In particular, the ability to compute genuine negativity for multipartite systems has eased this task.[43– 45] We find that under the non-Markovian amplitude damping, the Greenberger– Horne– Zeilinger (GHZ) state appears to be fragile as it does not repeat the collapse and revival of genuine entanglement for a long time. On the other hand, the W state turns out to be a most resilient state. All other quantum states of three and four qubits exhibit similar behavior to W-type states. We compare the dynamics of chosen quantum states with the dynamics of random pure states and weighted graph states.
The rest of this paper is organized as follows. In Section 2, we describe the model and equation of motion. In Section 3, we discuss the entanglement monotonicity and initial quantum states, which we study in this work. We present our main results in Section 4. Finally we summarize the paper in Section 5.
To study the effects of environmental noise on multipartite entangled qubits, we will consider a model in which each qubit is independently coupled to its local environment that consists of a wide spectrum of harmonic oscillator modes. The total Hamiltonian for each qubit thus reads (we take ħ = 1 throughout)

Here ω 0 is the energy separation between the qubit levels | 0〉 and | 1〉 (with energies ± ω 0/2, respectively), σ z is the Pauli-Z operator, and bk is the annihilation operator for the environment mode with frequency ω k. The last term HI in Eq. (1) describes the interaction between the qubit and its environment. To be specific, in this work we will consider amplitude-damping noise which arises from energy exchange between the qubit and the environment modes. Thus we have[46– 49]
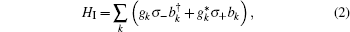
where gk are the coupling amplitudes and σ ± the raising/lowering operators for the qubit levels. We shall take the environment initially in the vacuum state at zero temperature. In this case, the qubit dynamics under the influence of the coupling (2) can be solved exactly.[50] The time evolution for the reduced density matrix ρ s for a single qubit can then be expressed as an operator sum[51]

where ρ s(0) is the initial density matrix for the qubit and Ei are the operation elements for the time evolution of the qubit, which account for the entire environment effects over the qubit and satisfy 

where 

subject to the initial condition p(0) = 1. Note that here we are using the interaction picture and have introduced the noise correlation function
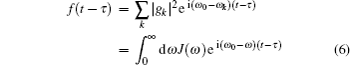
with J(ω ) the spectral function for the environment coupling.[48, 49]
For the entire system of qubits, since the qubits are not interacting with each other and their environment noises are not correlated, each of the qubits evolves independently in accordance with Eq. (3). The reduced density matrix ρ for the N qubits thus evolves as follows:

with ρ (0) being the initial density matrix for the N qubits. The operation elements here are tensor products of the single-qubit operation elements

where α = 1∼ N are the qubit labels and iα = 1, 2 denote the single-qubit operation elements in Eq. (4). In the following sections we shall analyze the time evolution of the qubit entanglement by making use of this result. For explicit calculations, however, it is necessary to have specific spectral function J(ω ) for the qubit-environment coupling. Here we will consider a Lorentzian spectral function[52]

where γ is the (phenomenological) decay rate for the upper qubit level | 1〉 , λ is the bandwidth of the coupling (thus λ − 1 is the noise correlation time), and Δ is the detuning from the resonance frequency ω 0. Utilizing Eq. (9) to Eq. (6), one can readily obtain the correlation function f and then solve for p(t) from Eq. (5), yielding[53]

where

With the explicit form for the function p, one can construct the single-qubit operation elements Eq. (4). By making use of Eqs. (7) and (8) given above, we are now ready for studying the time evolution of the qubit entanglement. For this purpose, we will begin in the following section by introducing the entanglement measure for the N-qubit system and discussing the initial states that will concern us.
In this section, we briefly review the concept of entanglement in multipartite systems and introduce the particular quantum states. The material in this section is already known in the literature and we cite it appropriately.
Let us take a system of three parties A, B, and C as an example. A state is defined to be biseparable if we could write it as a mixture of states across different bipartitions, that is

A state would be genuinely multipartite entangled if not biseparable. This definition is extendable for N parties.
Genuine entanglement can be detected and characterized via the technique of positive partial transpose mixtures (PPT mixtures).[43, 44] A bipartite state ρ = ∑ ijklρ ij, kl | i〉 〈 j| ⊗ | k〉 〈 l| is PPT if its partially transposed matrix ρ TA = ∑ ijklρ ij, kl | i〉 〈 j| ⊗ | k〉 〈 l| is positive-semidefinite. As separable states are always PPT[54] and therefore the set of separable states with respect to some partition is contained in a larger set of states which has a positive partial transpose for that bipartition. The states which are PPT with respect to fixed bipartition may be called 


which is called a PPT mixture. Because any biseparable state is a PPT mixture, any state which is not a PPT mixture must be genuinely entangled. The main benefit of employing PPT mixtures instead of biseparable states is that PPT mixtures can be fully characterized by semidefinite programming (SDP)[55] and the set of PPT mixtures serves a very good approximation to the set of biseparable states and delivers the best known separability criteria for many cases, however some PPT mixtures are also genuinely entangled.[43, 44] A state is a PPT mixture if and only if
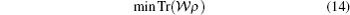
has a positive solution under the constraint that for all bipartitions M| M̄

The constraints reflect that 
Two important families of states, namely the GHZ states and the W states for N qubits are given as

A GHZ state always has the maximum value of monotone, that is, E(| GHZN〉 〈 GHZN| ) = 1/2, whereas for the W state, the numerical value depends on the number of qubits. For three qubits E(| W3〉 〈 W3| ) ≈ 0.443 and for four qubits E(| W4〉 〈 W4| ) ≈ 0.366.
Several interesting states for four qubits are the Dicke state | D2, 4〉 , the singlet state | Ψ S, 4〉 , the cluster state | CL〉 , and the so-called χ -state | χ 4〉 , given as

respectively. All these states are maximally entangled with respect to multipartite negativity,

Further details about these states may be seen in Ref. [2].
To get the relative behavior of these states, we compare their dynamics with those of random pure states and weighted graph states. The generation of these random states is described in Refs. [34]– [37].
In this section, we present our main results. First we would present results for three qubits and then for four qubits.
Let us first consider the Markovian limit, which may be obtained by taking the initial values of λ = 10γ and Δ = 0. In Fig. 1, we plot the genuine negativity for the GHZ state (black solid line), the W state (green dotted line), mean values of random pure state (MRS) (red thick dashed line), and the weighted graph state (MWGS) (blue thick dashed dotted line). Each of the mean value curves is the average of 100 random curves. We find that the GHZ state is the most fragile state and looses its genuine entanglement at about γ t ≈ 0.74. On the other hand, the W state is quite robust and remains genuinely entangled for a sufficiently long time. The mean values of random pure states and weighted graph states exhibit dynamics similar to the W state and also remain genuinely entangled for long times.
 | Fig. 1. Genuine negativity for various states is plotted against parameter γ t. We have taken the Markovian regime with initial values of λ = 10γ , and Δ = 0. |
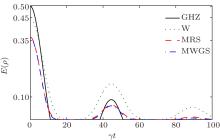
Let us now explore the effect of non-Markovian reservoirs on genuine entanglement with and without detuning. Figure 2 shows the time evolution of genuine negativity for the GHZ state (black solid line), the W state (green dotted line), the mean value of genuine negativity for random pure states MRS (red thick dashed line) and the mean value of genuine negativity for weighted graph states MWGS (blue thick dashed-dotted line). We have chosen the initial values of λ = 0.1γ , and Δ = 0. We observe that non-Markovian reservoirs delay the lifetime of genuine entanglement of the GHZ state till γ t ≈ 3.65 and after that there is no revival of its genuine entanglement. Whereas the genuine negativity of the W state comes to an end at γ t ≈ 8.15 and revives again at γ t ≈ 8.35. In comparison, the genuine negativity for both random states and weighted graph states comes to an end at γ t ≈ 7.7 and revives at γ t ≈ 8.85. In this respect the dynamics of these random states resemble the W state.
In Fig. 3, we depict the genuine negativity for various states in a non-Markovian regime. We take a relatively short reservoir correlation time and positive detuning with λ = 0.1γ , and Δ = 8γ . First, we note that again genuine negativity for GHZ does not exhibit any revivals and comes to an end at γ t ≈ 4.2, which means that positive detuning has slightly delayed the end of genuine negativity. On the other hand, the effect of positive detuning on the dynamics of genuine negativity for the W state is remarkable. There is no more collapse and revival of the genuine negativity and furthermore, the W state stays genuinely multipartite entangled for a very long time. This is due to the fact that enlarging detuning actually tends to decouple the qubits from reservoirs, hence the larger the detuning, the larger the decoupling will be and it will be no surprise that for sufficiently large detuning, the genuine entanglement of states under consideration is not effected at dawn all. The dynamics of random states and weighted graph states resemble each other and exhibit a revival peaked around γ t ≈ 55, however, the actual amount of entanglement after γ t ≈ 10 is very small.
 | Fig. 3. Same as Fig. 2 with initial values of λ = 0.1γ and Δ = 8γ . |
Let us now consider a relatively long reservoir correlation time by taking λ = 0.01γ , and zero detuning Δ = 0 in the non-Markovian regime. Figure 4 shows genuine negativity plotted against parameter γ t. We observe that a relatively long reservoir correlation time has further delayed the collapse of genuine negativity of the GHZ state to γ t ≈ 11.1. Moreover, for the GHZ state there is also one revival of genuine negativity at γ t ≈ 38.3 and again it collapses at γ t ≈ 51, after that there are no further collapses and revivals. The genuine negativity of the W state comes to an end at γ t ≈ 23.1 with a revival at γ t ≈ 23.6, it again collapses at γ t ≈ 67.5 with again a revival at γ t ≈ 68.2. The random pure states and weighted graph states again exhibit similar behavior to each other and to the W state.
Finally, we consider a relatively long reservoir correlation time with positive detuning, that is, for initial values of λ = 0.01γ , and Δ = 8γ . Figure 5 shows genuine negativity plotted for the GHZ state, W state, and mean values of random states. We find that genuine negativity for the GHZ state collapses at γ t ≈ 11.2, which is almost identical to the zero detuning case but the revival of genuine negativity is delayed to γ t ≈ 72.6, almost twice as later as the zero detuning case. For the W state there are no more collapses and revivals of genuine negativity and the state becomes quite robust similar to the short correlation time. Once again the random states exhibit similar behavior to the W state, except the difference is that after γ t ≈ 15, the amount of genuine negativity is very small at all times other than the interval 65 < γ t < 85.
 | Fig. 5. Same as Fig. 4 but for initial values of λ = 0.01γ and Δ = 8γ . |
Here we present results for various quantum states of four qubits discussed in the earlier section.
Figure 6 depicts genuine entanglement E(ρ ) plotted against parameter γ t for various states. We have set λ = 10γ , and Δ = 0 to achieve the Markovian limit. All the specific states except the W state show similar dynamics for some time before taking different trajectories. In comparison, the GHZ state again turns out to be the most fragile state and loses its genuine entanglement at γ t ≈ 0.56 earlier than the three-qubits case. The W state is quite robust and decays asymptotically similar to the three-qubits case. The monotone becomes zero at γ t ≈ 0.67 and γ t ≈ 0.98 for | χ 4〉 and | CL〉 states, respectively. Interestingly, the Dicke state | D2, 4〉 and | S4〉 state exhibit almost the same dynamics as their curves overlap and decay asymptotically. The mean values of random states (MRS) and weighted graph states (MWGS) almost exhibit similar behavior as for the three-qubits case.
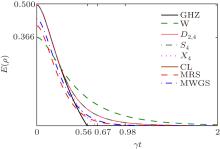 | Fig. 6. Genuine negativity for various states is plotted against parameter γ t. We have taken the Markovian regime with initial values of λ = 10γ and Δ = 0. |
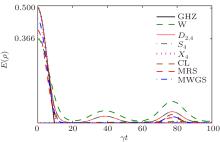
To study the effects of non-Markovian reservoirs, we first set λ = 0.1γ , and Δ = 0, which corresponds to a non-Markovian regime with a relatively short reservoir correlation time with zero detuning. Figure 7 shows genuine entanglement plotted against parameter γ t for specific and random states. One obvious effect of non-Markovian reservoirs is to delay the end of genuine entanglement of all states. We observe that genuine entanglement of the GHZ state comes to an end at γ t ≈ 3.2 with no revivals. The only clear revival is for the W state, whose genuine entanglement comes to an end at γ t ≈ 8.2 but revives immediately at γ t ≈ 8.4. There are also revivals for S4 and D2, 4 states with genuine entanglement ending at γ t ≈ 7.9 and γ t ≈ 7.8 with revivals at γ t ≈ 8.7 and γ t ≈ 8.8, respectively. However, the amount of genuine entanglement during the revival interval is too small to be noticed in the figure. The genuine entanglement of χ 4 and CL states end at γ t ≈ 3.5 and γ t ≈ 4.3 respectively, with no revivals. The mean values of random states and weighted graph states exhibit a similar dynamics with negligible revivals.
We set Δ = 8 λ to study the effects of detuning with a short reservoir correlation time. In Fig. 8, we plot genuine entanglement against parameter γ t for specific and random states. It can be observed that the W state, S4 state, and D2, 4 state turn out to be the most robust states as a result of setting the chosen value of detuning. Whereas the GHZ state, χ 4 state, and CL state are still fragile as their genuine entanglement vanishes at γ t ≈ 3.5, γ t ≈ 4.5, and γ t ≈ 5.5, respectively with no revivals. The mean values of random states and weighted graph states exhibit similar behavior with a revival but a very small amount of genuine entanglement.
 | Fig. 8. Same caption as Fig. 7 but with λ = 0.1γ , and Δ = 8λ . |
To study non-Markovian effects with a relatively large reservoir correlation time, we set λ = 0.01. Figure 9 depicts genuine entanglement plotted against parameter γ t for the zero detuning case, that is Δ = 0. The GHZ state first loses its genuine entanglement at γ t ≈ 10 and later exhibits a revival only between γ t ≈ 42.5 and γ t ≈ 47. The genuine negativity for the χ 4 state becomes zero at γ t ≈ 11 with a revival only between γ t ≈ 39.5 and γ t ≈ 50. The genuine negativity for the D2, 4 state first becomes zero at γ t ≈ 22.5, then immediately reappears at γ t ≈ 24.5, again it becomes zero at γ t ≈ 66.5 and reappears at γ t ≈ 69.5, each time with smaller amplitude. The S4 state exhibits almost the same behavior as the D2, 4 state. The genuine negativity for the CL state first becomes zero at γ t ≈ 13, exhibits two revivals between γ t ≈ 35.5 and γ t ≈ 54.5, and between γ t ≈ 87 and γ t ≈ 91.5. The W state exhibits quite robust behavior as expected. Throughout the dynamical process, it remains genuinely entangled except at γ t ≈ 68 where it is zero, however, the amount of entanglement between γ t ≈ 16 and γ t ≈ 31.5, and between γ t ≈ 58.5 and γ t ≈ 78.5 is very small. The mean values of random pure states and weighted graph states exhibit similar behavior with one clearly observable revival.
Finally, we set λ = 0.01γ , and Δ = 8λ to study the non-Markovian effects with a relatively long reservoir correlation time with positive detuning. The results are shown in Fig. 10. Interestingly, the GHZ state exhibits no revival whereas D2, 4 and S4 states again exhibit similar behavior with a strictly positive but small value of genuine negativity throughout the dynamical process. The state χ 4 exhibits one revival but it is too small to be observable at this scale. The CL state loses its genuine negativity at γ t ≈ 13.5 with a revival between γ t ≈ 69 and γ t ≈ 86. The W state remains genuinely entangled as was the case for three qubits. The mean values for random pure states and weighted graph states show almost the same behavior as the CL state.
At this stage, we want to remind the readers that our method to detect the genuine entanglement is not always perfect. If this measure is positive then the state is guaranteed to be genuinely entangled, however, if it is zero, then in general, we do not know whether the state is entangled or not, except for the GHZ state.
We have studied the behavior of genuine multipartite entanglement under non-Markovian amplitude damping. Using a computable entanglement monotone for multipartite quantum systems, we have observed the collapses and revivals of genuine entanglement for various quantum states of three and four qubits. We have compared the dynamics of the chosen quantum states with the dynamics of random pure states and weighted graph states so that we can make meaningful statements about their behavior under decoherence. For the three-qubits case, we have found that under the Markovian limit the GHZ state is fragile, whereas the W state is quite robust. The random states behave similarly to the W state. For the non-Markovian limit, we have two situations, that is, a short reservoir correlation time and a long reservoir correlation time, each case with or without detuning. For zero detuning and a short correlation time, the GHZ state is again fragile and exhibits no revivals, whereas the W state exhibits the collapse and revival phenomenon. Again the random states have a similar behavior to the W state. For positive detuning with a short correlation time, the GHZ state again reflects its fragility with no revivals, whereas the W state has remarkable dynamics. There are no collapses and revivals for the W state in this case and it stays genuinely multipartite entangled for a very long time. The random states again show similar dynamics like the W state but with a very small amount of monotone. For a long correlation time and zero detuning, the GHZ state exhibits only a single collapse and revival, whereas the W state exhibits multiple collapses and revivals. The random states follow the same dynamics as the W state. For a long correlation time and positive detuning, the GHZ state again exhibits single collapse and revival, whereas the W state does not undergo collapses and revivals and remains genuinely entangled for a very long time. The random states have similar trajectories like the W state with less amount of monotone. For four qubits, the Markovian limit case is identical to the three-qubits case. For the non-Markovian limit, a short correlation time and positive detuning, the GHZ state, χ 4 state, and CL state are fragile with no revivals, whereas the W state, S4 state, and D2, 4 state are the most robust states as they remain genuinely entangled throughout the dynamical process. For a long correlation time and zero detuning, all states exhibit multiple collapses and revivals except the GHZ state which shows only a single revival. Finally, with positive detuning, the GHZ state shows no revivals whereas all other states show multiple revivals and the W state remains genuinely entangled all the time. We stress here that our conclusions are based on a criterion whose positive value for a given quantum state is guaranteed to be genuinely entangled, however, for states which are not detected by this criterion, we are not certain about their entanglement properties. Nevertheless, this study has increased our understanding about these multipartite entangled states and is helpful for preparation of these states in experiments.
I would like to thank Dr. Wu Shin-Tza for our valuable discussion, reading the manuscript, and his positive comments. I am also grateful to Dr. Farhan Saif for his kind hospitality at the Quaid-I-Azam University, where the final part of this work was done. I am also thankful to the referee for his/her comments which brought some clarity to the manuscript.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|