The RED has been extensively described in the literatures.^{[26, 29]} Here we give a brief overview to bring out the details of the new implementation.

Except for the possible effect of insufficient sampling, the difference between the conformational distribution of all the multiple short trajectories and the equilibrium distribution P_eq(q) solely comes from the particular selection of the initial conformations, since every trajectory is generated by the same simulation algorithm that keeps the desired equilibrium distribution, only the initial conformations are different. Therefore, each conformation in the same trajectory should contribute equally to the final stationary property, but conformations in different trajectories may contribute to different weights. Then, the equilibrium ensemble average of any physical quantity A(q) is

where, w_i is the weight of the i-th trajectory. 〈 · · · 〉 _eq and 〈 · · · 〉 _i denote the average over the equilibrium distribution and the i-th trajectory respectively.

The weight of the trajectory is determined by the deviation of the initial distribution from the equilibrium distribution, thus,

here Ω _{init, eq}(q) ≡ P_eq(q)/P_init(q), and P_init is the initial distribution, while q_i0 is the initial confirmation of the ith trajectory. We can linearly expand Ω _{init, eq}(q) by a complete set of conformational basis functions {A^μ (q)}

Here, A⁰(q) ≡ 1 is explicitly written out, and the basis functions are assumed to orthonormalize each other under the initial distribution, 〈 A^μ (q) A^ν (q)〉 _init = δ _{μ ν} .

From Eqs.  (2) and (3), we can obtain a self-consistent equation of w_i,

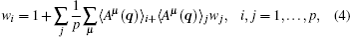
where p is the number of trajectories, 〈 · 〉 _i+ 〉 means the average in the initial part of trajectory i. Here we already set ∑ _iw_i = p without losing any generality.

Equation  (4) could be rewritten as G_i · w = 0 with i = 1, … , p, and G_i = (G_i1, … , G_iNt)^T, which can be regarded as a vector mapped from the i-th trajectory. We can write a symmetric equation,

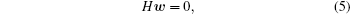
here, H = ∑ _iG_iG_i is the variance-covariance matrix of the trajectory-mapped vectors {G_i}, with at least one zeroeigenvalue as the ground state of H, and the ground state eigenvector gives the weights of all trajectories for reconstructing the global equilibrium distribution.^[26] By projecting the vectors, {G_i} to the H eigenvectors with zero (or near zero) eigenvalues, the trajectories are mapped into a lowdimensional space, where the non-transition trajectories inside different metastable states and the transition trajectories between these states can be identified easily.

In the RED, the selection of basis functions is crucial. The expansion in the RED require a complete set of basis functions in principle to guarantee the precision of Eq.  (3), thus the number of basis functions is usually very large.

In this paper, we present three kinds of methods to construct basis functions.

2.2.2. Method (ii): Cell functions of physical quantities

For the space spanned by a few characteristic physical quantities of a system, we could split the space into many discrete cells, and define basis functions based on the cells. Below is the procedure to construct these basis functions.

a) Equally dividing each physical quantity into n bins, then we have n^d grids in the space spanned by d quantities.

b) Collecting those grids containing sufficient sample conformations as cells. Empty grids are neglected, and some neighbouring grids with less sample points are merged into one cell. Each cell corresponds to a cell function, C^μ (q) = 1 if q is inside the μ cell, otherwise zero.

We first illustrate the method in a two-dimensional system. There are four major potential wells (I, II, III, and IV), shown in Fig.  1(a). 1500 simulation trajectories were generated at temperature 0.38 (in dimensionless unit). The initial position of every trajectory was randomly selected in the square region [− 2, 2] × [− 2, 2]. Each trajectory was simulated for 15 (in dimensionless time unit). More details are given in Appendix  A. We select 600 trajectories from all the 1500 trajectories with a non-uniform initial distribution, 250, 50, 50, and 250 trajectories starting from state I, II, III, IV, respectively, to test the ability of the RED in reproducing the equilibrium distribution.

We split the conformational space (x, y) into uniform n × n grids, and apply the cell functions as basis functions. Here, n = 10, see Fig.  1(b).

There exists only one zero eigenvalue of the H-matrix under T = 0.38, see Fig.  1(c), suggesting that the equilibrium properties of the system could be reproduced with current simulation data. The obtained weights of trajectories are plotted in Fig.  1(d), trajectories start from state I and state III have the same weights, with a small fluctuation. This is consistent with our supposition, that is, the weight of a trajectory mainly depends on the state where the trajectory starts. For simplicity, we count the samples in every state, and plot the counted number in Fig.  1(e). Due to its biased initial distribution and the short simulation time, the obtained sample distribution is different from the equilibrium one. In contrast, the reconstructed distribution is very close to the theoretical expectation. Although the initial distribution is biased, the changing of the trajectory weights offset the bias, leading to the equilibrium distribution. In order to estimate the error of the reconstructed distribution, we repeat the RED analysis 100 times by choosing different simulation trajectories. The error bar is the standard deviation of these results.

We project {G_i} to the second, third, and fourth eigenvectors of H, which maps each trajectory i to the point in a threedimensional space. Here is the α th eigenvector of H, and is always zero. In the threedimensional space, the 600 trajectories could be classified as shown in Fig.  1(f), where each point represents a simulation trajectory, and all the points together sketch out a tetrahedron. As expected, the points locate at the four vertices of the tetrahedron corresponding to the non-transition trajectories in the four states. The other points locate inside the lines, planes, or tetrahedron defined by the vertices correspond to the trajectories that visit two, three, and all four states, respectively. Most of the transition trajectories only visit two states, which lead to the line structures in Fig.  1(f). The line structure is consistent with the topology of the potential function, that is each vertex is only connected to two others by straight lines.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. (a) The two-dimension-four-state potential energy surface. (b) Splitting conformational surface into 10 × 10 grid. (c) The first ten eigenvalues of the H matrix. (d) 600 colored dots are trajectory weights of the 600 trajectories. (e) Reconstructed distribution (green bar), original distribution (blue bar) and theoretical value (dash line). (f) The projection of {Gi} to the second, third, and fourth eigenvectors of H.

2.2.3. Method (iii): RMSD-based-cell functions

Generally, it is possible to RMSD to split the sampled conformations into groups then construct basis functions. Here, RMSD is the measurement of the average distance between two conformations a and b,

where, n is the dimension of conformational vectors with the components, such as {a_i} and {b_i}. Basis functions could be constructed as follows.

a) Splitting Given a set of conformational samples, we randomly choose a conformation O₁ in the set as a reference, then calculate RMSD between O₁ and the other. The samples whose RMSD are smaller than a specified value are assigned into the same microstate or “ cell” of the O₁. The r¹ is called the radius of cell, and the number of samples inside the cell, n₁, is denoted as its size. Then, we randomly choose a second reference conformation O₂ out of the existing cells, and calculate RMSD between O₂ and all the others, to define the second cell O₂ (some samples may belong to both the first cell and the second cell, in other words, different cells could overlap). The aforementioned procedure is repeated until every sample in the set belongs to one or more cells. The number of cells is denoted by N. We limit both the radius and size n_i of the cell, to make sure is not very large and n_i is not very small, to avoid the systematic and statistical uncertainties, respectively. This issue is discussed in detail in Appendix  B.

b) Mapping Now any conformation sample S should be assigned to at least one cell, which is represented by vector {Aⁱ(S)} with the index of cells, i = 1 … N

where, RMSD(S, Oⁱ) denotes the RMSD between sample S and the center sample Oⁱ of cell i.

c) PCA It should be noted that the overlapping among the cells is quite large. We can employ principle component analysis (PCA) to orthonormalize these cell functions to form a set of complete orthogonal basis functions.

In the two-dimensional toy model (Subsubsection 2.2.2), RMSD between two samples is the geometrical distance between them. 41 cells are determined based on the RMSD matrix (Fig.  2(a)). Then, a two-dimensional coordinate (x, y) plane could be mapped onto 41-dimensional space (A¹, … , Aⁿ). As shown in Fig.  2(b), the first 36 eigenvalues account for over 90% of the sum of total eigenvalues. Thus, 36 corresponding eigenvectors are selected as basis functions. By using the RED, the reconstructed distribution is consistent with the theoretical value (Fig.  2(c)). Here, the number of cells is a tunable parameter. In this toy model system, actually, ten cells are sufficient to give good enough results (Fig.  8).

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) The 41 cells are shown as the blue circle. (b) The 41 eigenvalues in PCA analysis of cells. (c) Reconstructed distribution (green bar), original distribution (blue bar), and theoretical value (dash line).

The molecular structure of the short peptide Ace-(Gly)₂-Pro-(Gly)₃-Nme is shown in Fig.  3. This molecular is hydrophobic and its hairpin conformation is unstable in a solvent; ^[33] we simulate the system in a vacuum. The radius of gyration of heavy atoms (R_g) is a well-known slow variable, which is relatively straightforward to manually identify metastable states and get the equilibrium distribution from a conventional dynamics simulation. According to previous studies, ^{[31, 35]} the free energy along R_g has a “ doubel-well” structure, respectively corresponding to a globular and a β -hairpin folded conformation. Here,

where m_i is the mass of atom i and r_i is the position of atom i with respect to the center of mass of the molecule, and the sum run over all atoms except hydrogen.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The Ace-(Gly)2-Pro-(Gly)3-Nme peptide in a β -hairpin conformation (sketch).

(I) Simulation details

Initial configuration was generated using the PyMOL package. The MD data were obtained with the version 4.6.5 of the GROMACS simulation package^[36] and Amber96 force field.^[37] Simulations were carried out at 300  K using the v-rescale algorithm^[38] with a 2-fs times step and τ _T = 2  ps. The LINCS algorithm^[39] was applied to all bonds for constraints. The peptide was run in a vacuum with 12  Å cutoff for the nonbonded interactions.

We first use method (iii) to construct basis functions. RMSD between two structures is

here, , m_i is the mass of atom i, r_i(t) is the position of atom i at time t, and the summation runs over all backbone atoms (N, C_α , C). 500 conformations were first collected from a 20  ns simulation at T = 600  K. Then starting from these, we simulated 410 textrmns at T = 300  K. The first 10  ns of each trajectory is regarded as the relaxation process. The distribution of initial conformations along the R_g axis is shown in Fig.  4(a). There are 394 conformations in the “ globular” state (R_g < 0.41), and 106 conformations in the β hairpin state (R_g ≥ 0.41).

All 500 trajectories (400  ns) are used in the RED. The reconstructed distribution is shown in Fig.  4(b) (red line). The original distribution is very close to the reconstructed distribution, and the weights of trajectories are all around 1. It means that after 400  ns evolution, the system almost reaches equilibrium.

In order to verify the reliability of the RED, we only reserve the first 100  ns of every trajectory, and randomly discard 71 trajectories that started from the “ hairpin” state, then the remaining 429 100-ns trajectories (394 started from “ globular” and 35 from “ hairpin” ) are used in the RED. The distribution of raw data (non weighted) is shown in Fig.  5(b), which is very different from the equilibrium one. After the RED analysis, the weights of trajectories started from the hairpin are almost doubled, compared to previous results. As a consequence, the weighted distribution almost coincides with the reference distribution.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. (a) The distribution of 500 initial conformations along the Rg axis. There are 394 trajectories starting from the globular state, and 106 trajectories from hairpin state. (b) The blue line is the original distribution. The red line is the weighted distribution. Green points are weights of all trajectories. (c) The projection of {Gi} to the second and third eigenvectors of H.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) The eigenvalues of H. (b) There are 394 trajectories starting from the globular state, and 35 trajectories from the hairpin state. After 100  ns simulation, the distribution is far from equilibrium (blue line), green points are weights of trajectories, and the reconstructed free energy profile (red line) closely matches the reference value (black line).

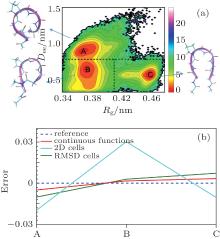
We project {G_i} to the second and third eigenvectors of H. In the two-dimensional space, the 429 trajectories are shown as points in Fig.  4(c). All points together sketch out a triangle, which means there are three meta-states, rather than the two states reported in the previous studies.^{[34, 35]} The conclusion of three states can be also found from the eigenvalue of H and the weights of trajectories. As shown in Fig.  5(a), there are n_s = 2 eigenvalues significantly smaller than one, which implies that this system has three (n_s + 1) metastable states. As shown in Fig.  5(b), the weights could be clustered into three clusters, corresponding to the three metastable states. By analyzing the conformations of these three states, we find that end-to-end distance (D_ee) of heavy atoms should be included as a new order parameter, the “ globular” state has two substates with almost the same radius of gyration R_g, but very different end-to-end distance D_ee. We plot the free-energy surface on the (Rg, D_ee) plane in Fig.  6(a), then we can divide the whole conformational space into three states, A, B, and C, as shown in Fig.  6(a). There are 181 trajectories starting from state A, which looks like a helix, 213 trajectories from state B, a “ globular” state, and 106 trajectories from state C, the “ hairpin” state.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. (a) Free energy surface on Rg– Dee plane, this plane can divide into three parts corresponding to three metastable states. (b) The error of reconstruct distributions of three methods. Horizontal axis is the index of three states. Vertical axis is the deviation of reconstruct distributions from the reference distribution.

(II) Comparison between three methods

In this subsection, we compare the performance of the three methods. Following the above procedure, we randomly discard 131 trajectories that started from region A, and analyze the remaining 369 (100  ns) trajectories based on three different basis function constructions.

First, six pairs ϕ – ψ of dihedral angles are used to construct basis functions by the method (i). The dihedral angles first need to be transformed to a linear metric coordinate space. This can be achieved by the transformation, ^[40]q_{2n− 1} = cosψ _n, q_2n = sinψ _n, where n = 1, … , M and M is the total number dihedral angles. Here, M = 12, so there are total 24 basis functions. After getting the weights of trajectories, we count the samples in three states, and plot the deviation of weighted distributions from the reference distribution in Fig.  6(b) (red line). Second, physical quantity-based cell functions are used to calculate weights of trajectories (method II). To be specific, we divide the R_g– D_ee plane into 100 equal grids. The deviation is shown as the cyan line in Fig.  6(b). Finally, we use the method (iii) to calculate the deviation between the RED results with the reference equilibrium distribution, which is shown as the green line in Fig.  6(b). It can be seen that all the three methods perform well for the short peptide system. For a system without enough priori knowledge, methods (ii) and (iii) might be better choices. More importantly, we could obtain a new order parameter to describe the system through analyzing the characteristics of conformations inside different states. Then we might use the order parameters to further enhance the sampling efficient, by using the advance simulation techniques, such as the umbrella sampling, ^[1] and metadynamics^[18] simulation.

Potts model is a generalization of the Ising model, a model of interacting spins on a crystalline lattice. It is often used as a model system to discuss phase transition.^[41] In this subsection, we use the RED to analyze the phase behaviour of the 2D Potts model. The Hamiltonian of the Potts model is defined as

where the summation is taken over all nearest neighboring pairs on the 2D lattice, each spin takes value q_i = 1, … , Q and δ is the Kronecker delta. In the following, we set N = L², L = 16, Q = 8, J = 1 and take the periodic boundary condition in the 2D lattice. RMSD between two conformations (a and b) is calculated as below:

here, is the q value of the i-th site of conformation a. However, symmetry arguments imply that, each conformation has N symmetric conformations. Here, we calculate the RMSD between all a’ s 256 symmetric conformations and b, and use the minimum value as the actual RMSD.

We generated 900 trajectories starting from random initial conformations at T = 0.7455. The length of every trajectory is 2200  MC cycles (1  MC cycle = N spin varying steps). The first 200  MC cycles are regarded as the relaxation process. The eigenvalue of H is shown in Fig.  7(a). There are nine eigenvalues which are significantly smaller than one, meaning that this system has nine metastable states. We project {G_i} to the second, fourth, and sixth eigenvectors of H to form a three-dimensional (3D) space (Fig.  7(b)), and the eighth eigenvector of H is represented and visualized as different colors of points. In this (3 + 1)-dimensional space, the 900 trajectories can be clustered into nine clusters. We find that the mean value of q of each conformation, is a good parameter to distinguish these clusters. Another commonly used order parameter m, ^[42] which takes the values 0 and 1 for completely disordered and ordered systems, respectively, is defined as,

where N_max = max(N_i) and N_i is the number of spins with the state q_i. We project all conformations to the m– q̄ plane. Obviously, in the two-dimensional space (m, q̄ ) (Fig.  7(c)), the 2D-8 states Potts model can be divided into nine meta-states, one paramagnetic state corresponds to the bottom state in Fig.  7(a), and the top eight states correspond to the eight ≡ alent ferromagnetic states with different q value.

In order to get a reference distribution, eight long trajectories were simulated at T = 0.7455. The entire run of each trajectory is 1.2 × 10⁸  MC cycles. Then, we count the number of samples in each ferromagnetic state and show the results in Fig.  7(d). The distance between each red point and the original point correspond to the number of samples in each ferromagnetic state. As shown in the figure, the number of samples in eight states are roughly equal, which implies that the system reaches equilibrium. The eight green points that compose a regular octagon could be taken as a reference line.

We also construct biased initial distribution and reproduce the equilibrium distribution by the RED. Here, we use method (iii) to construct basis functions. At T = 0.7455, 2000 trajectories were generated, and all of them are 2.2 × 10³  MC cycles long. The first 200  MC cycles are regarded as the relaxation process. We randomly select (150, 50, 50, 150, 150, 50, 50, 150, 50) trajectories that started from the eight ferromagnetic states and the paramagnetic state, respectively. Therefore, the initial distribution of the selected trajectories is very different from the equilibrium one. After 2 × 10³  MC cycles, the system does not yet reach equilibrium due to the short simulation time(Fig.  7(e) (blue line)). There exists only one zero eigenvalue of H, suggesting that the weights of trajectories can be calculated to reproduce equilibrium. The weighted distribution is plotted in Fig.  7(e) (red line), which is consistent with the theoretical value (black line). Although each single trajectory is short and far from equilibrium, the equilibrium distribution can be correctly reproduced by the RED.

Fig.  7.

Figure Option ViewDownloadNew Window

Fig.  7. (a) The eigenvalues of H. (b) The projection of {Gi} to the second, fourth, and sixth eigenvectors of H, the color of points corresponding to the eighth eigenvectors of H. (c) In the two-dimensional space (m, q̄ ), the trajectories can be clustered into nine states, one paramagnetic state and eight ferromagnetic states. (d) The samples in eight ferromagnetic states are expressed through a radar graph: the blue line is calculated from the simulation data, while the red dash line is the reference value. (e) The samples distribution (blue triangles), reconstructed distribution (red triangles), and reference distribution (black line).