†Corresponding author. E-mail: zhonghanhu@jlu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 91127015 and 21522304) and the Open Project from the State Key Laboratory of Theoretical Physics, and the Innovation Project from the State Key Laboratory of Supramolecular Structure and Materials.
Modern computer simulations of biological systems often involve an explicit treatment of the complex interactions among a large number of molecules. While it is straightforward to compute the short-ranged Van der Waals interaction in classical molecular dynamics simulations, it has been a long-lasting issue to develop accurate methods for the longranged Coulomb interaction. In this short review, we discuss three types of methodologies for the accurate treatment of electrostatics in simulations of explicit molecules: truncation-type methods, Ewald-type methods, and mean-field-type methods. Throughout the discussion, we brief the formulations and developments of these methods, emphasize the intrinsic connections among the three types of methods, and focus on the existing problems which are often associated with the boundary conditions of electrostatics. This brief survey is summarized with a short perspective on future trends along the method developments and applications in the field of biological simulations.
Along with the fast growth of computing resources in the supercomputing industry, molecular simulation techniques such as molecular dynamics (MD) simulation and Monte Carlo (MC) simulation have been used extensively for large systems of explicit molecules. A typical biological system usually consists of ions, macromolecules and water, whose motion and distribution may play important roles in producing various biological functionalities and thus are of great interest to both theoreticians and experimentalists in the fields of physical chemistry, biophysics and biochemistry. Typical experiments may not be able to directly elucidate the detailed structural and dynamical biological information involving the behavior of individual atoms, while simulations of explicit molecules can often provide direct molecular level understanding, and therefore it becomes a powerful tool to investigate biologically relevant systems such as ion solvation, water, protein or DNA solutions and other mixtures. Nowadays many biological systems can be simulated using popular software packages.[1– 7] The system simulated may contain up to a few million atoms and the time scale investigated might be up to a few milliseconds in supercomputers.
In classical MD or MC simulations, the interactions among atoms of molecules in a typical molecular force field usually consist of both intramolecular and intermolecular interactions.[8– 17] The intramolecular interactions mainly include bond stretching, angle bending, pair interaction, dihedral and improper dihedral, while the intermolecular interactions usually consist of the short-ranged Van der Waals (VDW) terms and the long-ranged (1/r) Coulomb terms.[17] In a typical biological system involving ions, water, proteins, nuclei acids or lipids, the electrostatic interactions often play an important role in determining the stabilities and the microscopic structure and dynamics of the macromolecules.[18, 19] Although VDW terms and all intramolecular interactions are effective in a range up to a few nanometers, for which a straightforward evaluation of the forces and potentials for a limited number of neighbours can be readily applied, it is a long-lasting and very challenging problem to accurately treat the Coulomb interactions.[20]
In this series of reviews, several topics related to electrostatics have been covered by a number of researchers in the field of liquid theory and simulations. An informative description of general electric double layer theories has been outlined by Yan and coworkers.[21] An insightful review of the optical response of peptide systems has been given by Zhuang and coworkers[22] who have shown that a simplified implicit treatment of electrostatics can often provide adequate physical explanations for a specific purpose. Moreover, molecular dynamics studies of ionic liquids and ionic solutions in response to an external electric field have been constantly focused by Wang’ s group[23– 26] which may provide guidelines for experimental designs of unexplored systems of interest. The importance of a detailed investigation of electrostatics under the usual periodic boundary condition may be related to other subtle problems as well. For example, Liu et al. argued that the multivalued property of the polarization was caused by the periodic boundary condition imposed on the system.[27]
Excellent reviews of the topic of accurate treatment of electrostatics in molecular dynamics simulations have been written more than a decade ago (e.g. Refs. [20] and [28]) and more recently.[29] In this short review, we will briefly discuss three types of related methods for electrostatics: truncation type methods (Section 2), Ewald-type methods[30] (Section 3) and mean-field-type methods[31– 35] (Section 4). Two of them, the truncation-type methods and the Ewald-type methods have been reviewed previously[29] however, we will take a different perspective by only focusing on the very recent development toward understanding the associated boundary issues.[36– 38] Therefore, this part of the review is supplementary to the existing excellent reviews. The mean-field-type methods have not been reviewed before and we will discuss their advantages and connections to the truncation type methods and the Ewald-type methods. We do not cover the detailed derivation but instead discuss the physical basis of each method. The main purpose of the discussion in this brief survey is to help illustrate the intrinsic connection among these methods. The review will be summarized with a short perspective on future trends along the methods development and applications in the field of computer simulations of biological systems.
As the VDW interaction can often be truncated when the distance is larger than a cutoff distance, it was suspected that truncation methods might work well for the Coulomb interaction. In the early 1990s, many researchers have realized that the truncation method often leads to unrealistic behavior of the system in the simulation.[18, 19, 39] However, some more recent simulations still implement the truncation method perhaps because of its intrinsic simplicity and low computational cost compared to other methods.[40, 41] In this section, we provide a basic formula for the straightforward cutoff method and the group-based truncation methods followed by discussing an interesting observation of the artifacts of the group-based truncation method when large cutoff distances are used.
For a unit cell of N point charges: q1, q2, … , qN located at r1, r2, … , rN. The Coulomb energy of this unit cell in the straightforward cutoff method is written as
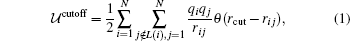
where rcut is the cutoff distance, the Heaviside step function is θ (x) = 0 for x < 0 and θ (x) = 1 for x ≥ 0, and L(i) is the intramoleclar neighbor list of the i-th charge. L(i) usually includes the i-th charge itself and any other charge that has already interacted with the i-th charge via the intramolecular interaction. The interaction between the i-th charge and any of its intramolecular neighbors is therefore excluded in Eq. (1). The distance between the two charges rij ≡ | ri − rj| is usually taken as the minimum distance among their images subject to the periodic boundary condition (PBC). This direct consequence of the PBC is also called the minimum image convention.[42] In the above equation and the following equations, we have omitted the prefactor 1/(4π ɛ 0) for simplicity.
Alternatively, one may introduce the group-based cutoff (GB-cutoff) method such that any charge always interacts with particles that are overall neutral. Suppose there are M neutral groups in the unit cell, each of which includes Nm charges for m = 1, 2, … , M, we denote the charge and the coordinate of the j-th charge in the m-th group as qj(m) and rj(m) respectively. The electroneutrality condition for each group is then written as 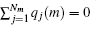

where 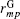
One disadvantage of the above truncation methods is that the potential is not continuous at the boundary of the cutoff distance, which can be seen from the use of the Heaviside function in the Coulomb energy. For the cutoff approach, it has been intuitively believed that increasing the cutoff length and using the group-based cutoff strategy might make the simulation result more accurate and reliable. But in 2005 Yonetani[43] reported that by setting the cut-off length as large as 1.8 nm, a bulk water simulation of TIP3P model water surprisingly produces a spurious layer structure. These results have indicated that for the uniform and neutral system, the truncation method unexpectedly generates significant artifacts. Soon after that, van der Spoel and van Maaren[44] simulated a series of water systems and calculated the electrostatic interaction via different methods to give a reasonable explanation for the spurious structure found by Yonetani.[43] These works concluded that only the appropriate simulation parameters can avoid the artificial phase transition. When the layer structure is produced by the use of the truncation method, the density increases, the potential energy reduces and water diffuses anisotropically. From the dipole– dipole correlation, they found that there are a large number of water molecules oriented similarly around a given one, and after some width of such a cluster, a larger number of water molecules orient oppositely. The underlying reason is that each water molecule and its surrounding molecules form a cluster in the vacuum followed by the decrease of the free energy through minimizing its net polarization. Simultaneously the periodic boundary condition strengthens the formation of the artificial layer structure.
Although the truncation methods are efficient and easy to implement, the associated defects seem inevitable at least for some specific systems relevant to biological simulations. The above interesting finding of the artifact of the truncation method is definitely not intuitive. Therefore, it indicates that properties of specific systems could potentially be very sensitive to the accurate treatment of the electrostatics. As water is the most important system relevant to biological functionality and activity, the above finding essentially suggests that very careful checking needs to be done when the truncation methods are used for simulations of biological systems.
Unlike the truncation methods, Ewald-type methods compute the Coulomb lattice sum by explicitly considering the presence of the images when the system is subject to the periodic boundary condition.[30] Various Ewald-type algorithms have been developed in the past and have been coded in major simulation packages and hence have generated more than 104 citations for the basic papers in the past decade. Topics along this line have been extensively reviewed (e.g. Refs. [28] and [29]) and therefore are not repeated here. This section only focuses on very recent developments that contribute alternative understandings of the boundary condition associated with the Coulomb lattice sum.[36– 38]
The basic idea of the Ewald sum is to divide the Coulomb interaction into the short-ranged part and the long-ranged part using a screening factor α
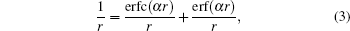
where erf(x) and erfc(x) ≡ 1 − erf(x) are the error function and the complementary error function respectively. The corresponding short-ranged part (the complementary error function part) of the Coulomb lattice sum is then summed in real space as usual but the long-ranged part (the error function part) is summed in reciprocal space. By defining an infinite boundary term associated with the behavior that the system asymptotically approaches the infinite, it has been recently shown that the Ewald sum for electrostatics in a system that is periodic in one (Ewald1D), two (Ewald2D) or three (Ewald3D) dimensions can be written as a sum of pairwise interactions.[37] For a system of point charges in bulk, the usual Ewald3D sum for N charges in the rectangular unit cell is thus written as[37]

where the real space sum, the reciprocal space sum and the infinite boundary term for the system of 3D periodicity are,
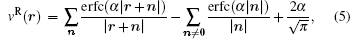

and

respectively. The vector n stands for (nxLx, nyLy, nzLz) in which nx, ny, and nz are integers and Lx, Ly, and Lz are the length of the unit cell in the three directions respectively. V = LxLyLz is the volume of the unit cell. The corresponding reciprocal vector k is defined as k ≡ 2π (kx/Lx, ky/Ly, kz/Lz), k = | k| , and kx, ky, kz are all integers. In fact, the pairwise form and the infinite boundary term are not unique for 3D periodicity and the similar definitions can be made for the 3D system with reduced 2D (Ewald2D) or 1D (Ewald1D) periodicity.[37] The clear definition of the pairwise potential might be important for various understandings of the Ewald sum. For example, the purpose of a biological simulation is often to provide molecular level insight for the effect of a particular selected group of particles on another selected group of particles. However, the presence of the explicit images make it difficult to exactly split the total electrostatic energy into pairs. The usual way of analyzing the real space part of the Ewald sums depends on the choice of the screen factor α . In contrast, the unique definition of v(r) in bulk immediately solves this problem because v(r) does not depend on α any more. Similarly, v2D(r) and v1D(r) for systems in reduced periodic dimensions[37] are useful for the analysis of the trajectory when the corresponding Ewald2D or Ewald1D method are used to simulate interfacial biological systems.
Although the pairwise potential v(r) is conceptually useful, the pairwise form by itself does not directly produce an efficient algorithm. In practice, the widely used particle mesh Ewald (PME) algorithms[45– 47] interpolate the usual reciprocal (Fourier) space term part of the Ewald3D sum on a grid and then utilizes the computationally 
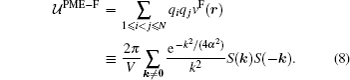
In the popular smoothed particle mesh Ewald algorithm, [46] a powerful B-spline interpolation scheme is used for the structure factor 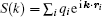
The Ewald3D sum consisting of the real space sum and the reciprocal space sum (vIB = 0) is usually regarded as the standard method to validate other algorithms. One particular truncation method that is closely related to the Ewald method is the Wolf truncation method[49] in which the real space sum of the Ewald sum is used and the reciprocal space sum is ignored. For biological systems in a crowded environment under the condition of constant volume, the success of the Wolf truncation method or the real space part of the Ewald sum might be understood because the force associated with the long-ranged component in the reciprocal space part essentially cancels each other. However, the virtues and defects of the above discussed truncation methods or any other spherical truncations of Coulomb interaction for biological simulations remains a subject of ongoing debate.[50] Nonetheless, the real space part of the Ewald sum provides an alternative efficient 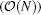
Although the Ewald sum without the infinite boundary term has been regarded as the standard method in computer simulations of liquid systems in general, a number of artifacts associated with the explicit presence of images were discussed in the literature. We list three types of the potential artifacts in the following. Because the Coulomb lattice sum is a conditionally convergence series, the Ewald sum might in principle have an extra conditional term. This term was called the surface or dipole term[42] but ambiguity exists because the dipole of the unit cell is not well defined. In most applications of the Ewald-type methods including the PME methods, the conditional term is usually ignored and the resulting Ewald sum with the real and reciprocal sums only is called the Ewald sum with the tin-foil condition boundary corresponding to the physical situation that the macroscopic system is surrounded by a conducting metal.[42, 51] When the boundary condition is written as the pairwise infinite boundary term of Eq. (7), the alternative formulation in principle removes the ambiguity such that the computation for a given infinite boundary term is not problematic any more. However, it is still unknown which infinite boundary term or which path of k → 0 should be chosen for certain purposes in computer simulations of liquid systems.[37]
Besides, Smith and Pettitt have reported that there exists an energy barrier when a dipole rotates in the simulation box with its center fixed.[52] In fact, this broken symmetry of rotational invariance can be clearly seen from the fact that the pairwise potential v(r) depends on the vector r instead of the scalar r. This effect might contribute little to the property of the system because the electrostatic interaction is screened by a large dielectric constant for most bulk liquids (e.g., the dielectric constant of bulk water ɛ 0 ≃ 80).
For the charged system, the classical Ewald summation should be added by a correction term as a result of adding a uniform neutralizing charged background plasma. Many researchers[53– 56] have pointed out the periodicity-induced artifacts when dealing with the charged system with the Ewald summation method, and given their corrections. However Bogusz et al.[57] pointed out that such a uniform neutralizing background plasma brings forth serious artifacts to both the system energy and pressure. They also instituted a net-charge correction term to correct these problems. What is more, Hü nenberger and McCammon[55] performed the detailed investigation on the Ewald artifacts in computer simulations of ionic solvation and ion-ion interactions. Based on continuum electrostatics and two examples both comparing the non-periodic boundary condition and periodic boundary condition, they summarized three factors which may enlarge the periodicity-induced artifacts. No matter what, the finite size effect generated by the periodic boundary condition is widely believed to be corrected by self-energy, which was proposed[58] and examined on the analysis of free energy of ionic hydration. Ekimoto et al.[56] recently presented a similar correction scheme for the free energy of charged protein in an explicit solvent.
The above three aspects of the Ewald artifacts are ongoing topics in this field. We believe that the problem of removing the artifacts associated with the Ewald sum has not been settled in principle although the Ewald type method is by far the standard method for the bulk system.
Mean-field-type methods in general suggest that a certain component of the long-ranged part of the intermolecular interaction can be replaced by an effective single-particle external field.[31, 59, 60] Mean-field ideas have been implemented in various molecular simulation techniques for simple and complex molecular liquids[31– 33, 35, 61– 64] and analytical theory.[31, 65] The mean-field-type methods for electrostatics are an important part of the local molecular field theory (LMF) originally developed by Weeks and coworkers.[31– 33, 61– 64] Using the idea of LMF and further introducing the dynamical effective field, another mean-field-type method called symmetry-preserving mean field (SPMF) theory was also recently developed.[35] This section is far from a comprehensive review of the full depth and breath of LMF but rather provides its basis and its connection to the truncation methods and the Ewald-type methods.
LMF theory maps the structural and thermodynamical properties of a complex system with long-ranged intermolecular interaction in a general external field into those of a simple system with only short-ranged intermolecular interaction but under a reconstructed effective external field. When the basic Coulomb interaction 1/r is separated into a short-ranged component v0 and a long-ranged component v1: 1/r = v0(r) + v1(r). The LMF theory suggests that the reconstructed external electrostatic potential 
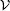
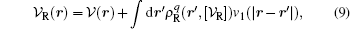
where 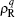
When the external field has a certain symmetry in the direction of β (e.g. planar symmetry rβ = z or spherical symmetry rβ = r), one can alternatively introduce the mean field approximation for the instantaneous configuration:[35]
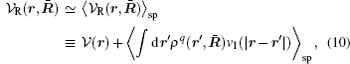
where 〈 〉 sp is the symmetry-preserving operator defined as the normalized integration over the degrees of freedom in the directions with no broken symmetry (other than β ). R̄ denotes the collective coordinates of all charges and ρ q(r, R̄ ) is the instantaneous charge density. An expansion of 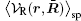

It has been argued that when the long-ranged component is slowly varying, only a small number of terms in the above series are needed to achieve high accuracy.[35] Therefore, the reconstructed field reaches the virtue of single-particle potential as it is in the LMF theory. Both the LMF and SPMF theories yield 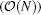
For the system of bulk solutions with translational and rotational invariance symmetry, the symmetry-preserving operator yields a constant and therefore the long-ranged components essentially cancel each other, which is equivalent to the strong coupling approximation in LMF theory[34] or the Wolf truncation method. Obviously, both the SPMF and LMF theories are more physically based with a clear explanation of the cancellation effect in bulk. This suggests that analysis of the defects of the truncation methods might be achieved in the framework of the LMF theory via considering the failure of the strong coupling approximation.
The Ewald separation suggests the use of v0(r) = erfc(α r)/r for the short-ranged component and correspondingly v1(r) = erf(α r)/r. Although the general framework of the LMF theory can be applied to any other separations as well, the Ewald choice is a very convenient choice in practice. Because erf(α r)/r essentially arises from a normalized Gaussian distribution with width 1/α , the reconstructed external field in the LMF theory exactly satisfies Poisson’ s equation but with a Gaussian-smoothed charge density given by the convolution of the point charge distribution with the normalized Gaussian distribution. This property allows many convenient and accurate applications of the LMF and SPMF theories as well. Moreover, corrections to thermodynamics in strong coupling approximation of the LMF theory can be done analytically when the Ewald choice is used.[61] This previous finding would suggest that perhaps the Ewald separation is the optimal choice for the practical application of the mean-field-type methods to accurately treat electrostatic interactions. However, a solid justification in principle has yet to be developed.
Because detailed studies of biological systems may often provide direct connection to experimental observations, applications of various types of method for different boundary conditions (bulk or interfaces) might be of particular interest. Recent development of efficient Ewald-type methods for interfaces[35, 36, 38] have been applied for systems of water and ions, which are obviously biologically relevant. Future applications of these methods might be expected for macromolecular aqueous solutions. A comparison of the efficiency and accuracy among the mean-field-type methods and the Ewald-type methods might be a topic of interest in the future.
Although the artifacts of the above reviewed methods have been discussed via detailed studies of specific systems, the underlying principles of avoiding certain artifacts may require much deeper investigation in the future. For example, it has been explicitly shown that the regular Ewald method without the infinite boundary term[37] (or equivalently the Ewald method with the tin-foil boundary condition) essentially violates the thermodynamical argument about the dielectric response in bulk water.[35] It is expected that many interfacial water or other biological systems previously studied by other people may suffer from the similar artifact when the long-ranged electrostatics is treated by the popular Ewald-type methods. However, a detailed report from a comparison of various types of methods will be still very useful to alert researchers in the field of liquid simulations. The mean-field-type framework discussed here might be useful to shed light on the existing problems as it has been shown that the efficient mean-field method can be used to obtain accurate structures, dynamics, and thermodynamics.[35] From the viewpoint of essential theoretical developments, one would like to predict rather than calculate certain structural and dynamical properties associated with the use of specific methods, which still has a long way to go.
Hu Zhong-Han would particularly like to thank Prof. Hans C. Andersen for his comments and suggestions on the first version of our work[
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 | [Cited within:2] |
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|


