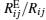Understanding transport processes in disordered media is of great relevance to many scientific fields, ranging from condensed matter physics to petroleum engineering.^{[1– 3]} It is a common way to model the disordered media as complex networks and the transport processes in them can in many cases be modeled as currents flow in random resistor networks. Network structure has a paramount impact on the transport processes, and such impact reflects the transport property of the network, which may be quantitatively represented by the statistics of the two-point resistance R_{i j}, or equivalently the two-point conductance G_{i j}, between any pair of node i and node j in the network. An elegant result^[4] was obtained that for a scale-free (SF) network^[5] whose degree distribution is with α > 2 and k_i being the degree of node i, the distribution of G_{i j} scales as , indicating the “ anomalous” nature of transport in SF networks, which is different from that in Erdő s– Ré nyi (ER) networks.^[6] Moreover, another striking, and perhaps more fundamental, result is that there exists a scaling function f (x) ≈ x/(1 + x) and G_ij ∼ k_jf (k_i/k_j) for both SF and ER networks.^[4] We note Φ (G_ij) is a direct outcome of this scaling function because Φ (G_ij)∼ ∬ P(k_i)P(k_j)δ (k_jf(k_i/k_j)− G_ij)dk_idk_j. In fact, for networks in which such a scaling function is present, one can easily obtain the knowledge of networks’ transport properties from the statistics of G_{i j}. Then, a natural question arises that whether there exists some similar relation for other types of networks. In this work, by systematically investigating various types of complex random networks encountered in nature and science, we numerically observe the simple relation

holds for all types of networks considered, as long as they are not too sparsely connected. Equation  (1) is essentially equivalent to the G_{i j} scaling found in Ref.  [4] for SF and ER networks, where a physical “ transport backbone” picture was provided to interpret it. Meanwhile, here we take advantage of the localization property of Laplacian eigenvectors to show why equation  (1) holds for networks considered in this work, and we expect the localization of Laplacian eigenvectors is present for general non-sparse networks, hence we conjecture that equation  (1) is actually a universal relation. This finding paves the way to infer transport properties of general non-sparse complex networks only from the degree distribution. In addition, equation  (1) can be used to estimate two-point resistance when the network structural information can only be partially or locally known.

We consider a complex network as a resistor network represented by the adjacent matrix A, with A_ij = 0 if node i and node j are not connected or A_ij = 1 if node i and node j are connected by a resistor of unit resistance. The voltage of node i is denoted by V_i. To calculate the two-point resistance, we inject a constant current I to node i and through node j the current flows out of the resistor network, then, the two-point resistance with respect to nodes i and j is R_ij = (V_i − V_j)/I. The net current for any node m can be written as I_m = I(δ _mi − δ _mj). The Kirchhoff’ s law states that

where L is the Laplacian matrix of the network with its component L_ij = k_iδ _ij − A_ij, and V and I are the vector forms of voltage and net current, respectively. We numerically solve V_i and V_j to obtain R_{i j}, and we estimate R_{i j} by

Results for various networks below show that for dense network connections the ratio is distributed narrowly, so practically equals R_{i j} up to a constant C. We fix network size N = 1000 in this work for all types of networks; increasing N will not qualitatively change our results.

2.2. Exponential networks

Exponential (EXP) networks refer to networks with exponential degree distribution, which is commonly observed in rock pore networks^[7] and other networks such as North America power grid.^[8] To generate this type of network, we use the method in Ref.  [5] by growing the network with each newly introduced node with k_min links connecting to existing nodes with equal probability. In Fig.  1 we plot as a function of k_min, where 〈 · · · 〉 denotes average over all possible pairs of i and j for a given network; equation  (1) is evident as the network is becoming densely connected.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. The average value of is plotted as a function of the minimum degree kmin for EXP networks with N = 1000. Inset shows typical distributions of for EXP networks with different kmin.

2.3. Small-world networks

To generate small-world (SW) networks, ^[9] we start from a regular ring lattice with each node connecting to its 2k_nn nearest neighbors, and we rewire each link with a probability p_r while keeping the total number of links fixed. As can be seen in Fig.  2, as the network is getting more densely connected by increasing k_nn and p_r, the estimation of R_{i j} by is better. Although SW topology most strongly manifests itself for p_r ∈ (0.001, 0.1), ^[9] the network generated with larger values of p_r still possesses both a substantially higher clustering coefficient than that of a random network, and a shorter average path length as compared with a regular lattice. So we argue our estimation is practically valid for SW networks with relatively high rewiring probability.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The average value of is plotted as a function of the rewiring probability pr for SW networks with N = 1000 and different knn. the inset shows typical distributions of for various values of pr and knn.

2.4. Clustered networks

The clustered networks are generated as in Ref. [10]. Nodes in the same cluster are randomly connected with probability p_in, while nodes in different clusters are connected with probability p_out. Without the loss of generality, we fix p_in = 0.8. We also let the number of clusters in the network be N_c = 10. Again, we observe in Fig.  3 better estimations of R_{i j} by appearing as the network is becoming more densely connected by increasing p_out. It is worth noting that for p_out = 0.1, is almost surely to be 1, indicating the effective estimation of R_{i j} by , while in the meantime, the links between different clusters are still distinguishably sparse as compared to those within the same clusters, say, p_in ≫ p_out. This fact implies that the condition under which equation  (1) holds does not lead to the deterioration of the network’ s clustered structure. In other words, the links in clustered networks on the one hand can be considered to be dense enough to validate Eq.  (1), while on the other hand, the intra-cluster links are still sparse enough to preserve the macroscopic clustered connectivity pattern of the network.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The average value of is plotted as a function of pout for clustered networks with N = 1000, pin = 0.8, and Nc = 10. Inset shows typical distributions of the ratio is as a function of pout.

2.5. Non-sparseness of networks

We have shown the validity of Eq.  (1) for various types of random networks as long as they are non-sparsely connected. However, the precise definition of “ non-sparseness” seems elusive, partly because of the fact that estimating R_{i j} by displays a tendency that as the number of random links in a network is increased, from a probabilistic point of view, both the ratio becomes centered towards 1 and at the mean time its standard deviation σ _E is diminishing. Practically, it is possible to set some threshold for σ _E, for example 0.05, as a measure to quantitatively reflect how densely connected the network is, while mathematically, we fail to find a natural criterion for non-sparseness.

Nonetheless, we argue non-sparse random connections are expected to be encountered in random networks with a fairly large size and without a local tree structure. (In fact, a local tree structure is routinely used as a feature of “ sparse” networks.) To further address this point, we define the coefficient of variation c_v for the ratio as

Intuitively, if a network is sparsely connected, then σ _E is large, and so is c_v. As the network becomes more densely connected, σ _E is diminishing, resulting in an also vanishing c_v. In Fig.  4 we plot for SF networks how c_v is changed as N and k_min are increased. (Though it might be problematic to refer to a network with N < 100 as an SF network, we generate networks with different N from the same preferential attachment rule to see the effect of network size N on the estimation of R_{i j} by .) Typically, c_v is decreased as the latter two are increased, indicating better estimation of R_{i j} by . For k_min ≥ 5, a network with N = 1000 contains dense enough random connections to practically validate Eq.  (1). For k_min < 5, it seems inappropriate to consider a network with N = 1000 as a non-sparse one, however, c_v still shows a deceasing tendency as N is increased. Meanwhile in the case of k_min = 1, the network is strictly a tree, and numerically we observe no decreasing tendency of c_v as N is increased, indicating that Eq.  (1) is by no means valid in this case.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The coefficient of variation cv for is plotted for SF networks with different N and minimum degree kmin. Here, cv is diminishing as both kmin and N are increased, implying the validity of Eq.  (1) for non-sparse network connections.

Qualitatively similar results can also be found for other types of networks, and it is interesting to investigate in more detail how the non-sparseness condition can be achieved in a network in the future, however, this is beyond the scope of the present paper. Despite the term “ non-sparse” being mathematically not rigorously defined, we use it in a practically unambiguous way to refer to typical complex networks encountered in nature and technology which contain thousands of nodes that are usually connected to more than one neighbor.

We will show in the following that the localization of Laplacian eigenvectors can be used to explain Eq.  (1) for all types of networks considered in this work, and possibly for other types of non-sparse complex random networks. Our analysis rests heavily on the theory developed in Ref.  [11], where the exact value of R_{i j} is obtained using eigenvalues and eigenvectors of the Laplacian matrix L as

where U_{i j} is the i-th row j-th column element of a matrix U, whose m-th column is the m-th eigenvector, u_m, of L, and λ _m is the associated m-th eigenvalue in ascending order with 0 = λ ₁; Ψ _i, Ψ _j, and ψ _ij are defined to be the three terms on the right-hand side of Eq.  (3), respectively. Equation  (3) is an exact result that applies to any network, and it has been used to calculate R_{i j} for regular lattices.^[11] This work has aroused much interest, and more sophisticated situations have recently been considered.^{[12, 13]} However, we use the method to numerically compute R_{i j} for non-sparse random networks and we find actually Ψ _i and Ψ _j suffice to effectively estimate R_{i j} because typically we have

for all kinds of networks considered in this work.

A systematical investigation over typical distributions of | ψ _ij| /(Ψ _i + Ψ _j) for various types of networks is conducted, and results are shown in Fig.  5 with a fixed N = 1000. The SF networks with k_min = 3 and k_min = 10; ER networks with p = 0.006 and p = 0.1; EXP networks with k_min = 3 and k_min = 10; SW networks with p_r = 0.06 and p_r = 0.6 (k_nn = 3); SW networks with p_r = 0.06 and p_r = 0.6 (k_nn = 5); clustered networks with p_out = 0.001 and p_out = 0.05 are shown in Figs.  5(a)– 5(f), respectively. For each type of network, the corresponding typical distribution is not necessarily similar to those of other types of networks, and the specific distribution itself, though worth studying, is not our main interest at present. Rather, we focus on the effect of increasing random connections in networks on the distributions. In all the cases, as the random connections among nodes in networks are denser, distributions shift leftward, i.e., | ψ _ij| is more likely to be negligible as compared with Ψ _i + Ψ _j, validating the inequality  (4). This fact implies that for non-sparse random networks we can rewrite Eq.  (3) as

Fig.  5.

Figure Option ViewDownloadNew Window

Fig.  5. Typical distributions of | ψ ij| /(Ψ i + Ψ j) are plotted for various types of networks with different parameters and a fixed N = 1000. (a) SF networks with kmin = 3 and kmin = 10; (b) ER networks with p = 0.006 and p = 0.1; (c) EXP networks with kmin = 3 and kmin = 10; (d) SW networks with pr = 0.06 and pr = 0.6 (knn = 3); (e) SW networks with pr = 0.06 and pr = 0.6 (knn = 5); (f) clustered networks with pout = 0.001 and pout = 0.05.

Moreover, our numerical results further reveal that Ψ _i actually displays a strong linear dependence on for non-sparse networks

inserting which into Eq.  (5), one finds Eq.  (1). To validate the linear dependence of Ψ _i on 1/k_i, we show in Fig.  6 the results for SF, ER, and EXP networks, in which the linear dependence is most pronounced as k_min = 10 for SF networks, p = 0.1 for ER networks, and as k_min = 10 for EXP networks, respectively, with each case corresponding to the most densely connected network considered here. The results for SW and clustered networks are presented in Fig.  7; it is also straightforward to see that for SW networks, the linear dependence best manifests itself when k_nn = 5 and p_r = 0.6, and for the clustered networks, when p_out = 0.05. Again, in both cases, the corresponding networks have dense enough random connections.

Fig.  6.

Figure Option ViewDownloadNew Window

Fig.  6. Ψ versus 1/k is plotted for SF, ER, and EXP networks (N = 1000). No relation between Ψ and 1/k is observed for extremely sparsely connected SF and EXP networks with kmin = 1. For the ER network with p = 0.006 the linear dependence is approximate, while an evident linear dependence is observed as kmin = 10 for SF and EXP networks, and as p = 0.1 for ER networks, corresponding to more densely connected networks in all the cases.

Fig.  7.

Figure Option ViewDownloadNew Window

Fig.  7. Ψ versus 1/k is plotted for SW and clustered networks (N = 1000). For SW networks, both with knn = 3 and knn = 5, the linear dependence of Ψ on 1/k does not manifest itself for a low rewiring probability pr = 0.06, but it does appear for a high rewiring probability pr = 0.6, and the case in which knn = 5 and pr = 0.6 shows the best linear dependence of Ψ on 1/k. For clustered networks, the linear dependence is also more evident as the inter-cluster connection probability pout is increased.

With the above numerical results, we can conclude that for non-sparse random networks, equation  (1) is a natural outcome of Eq.  (3) when the inequality  (4) and the linear dependence  (6) are taken into account. However, why do the latter two hold? We argue that this can be understood via the localization property of Laplacian eigenvectors. To proceed, we let the degrees of all nodes in a network be sorted in ascending order such that k₁ ≤ · · · ≤ k_N. By localization, we mean the dominant part of components of the Laplacian eigenvector u_m, which is associated with the m-th eigenvalue λ _m, lies on the nodes that have degrees close to k_m.^{[14– 17]} We plot in Fig.  8 how the components of Laplacian eigenvectors are distributed on nodes. Nodes in a network are divided into groups based on their degrees; nodes with the same degree belong to the same group. For example, nodes in group i all have the same degree K_i. If a network has N_d groups, then we can denote the distinct degree sequence of such groups in ascending order as k₁ < · · · < k_Nd; note that N_d is almost always less than N in a random network. We next compute the fraction, denoted f_nm, of the m-th Laplacian eigenvector that is distributed in the group in which nodes have degree K_n

Fig.  8.

Figure Option ViewDownloadNew Window

Fig.  8. Localization of Laplacian eigenvectors is shown for five types of networks. The network size is fixed to be N = 1000. We compute fnm for each Laplacian eigenvector um, whose corresponding eigenvalue is λ m. The diagonal pattern implies the localization of Laplacian eigenvectors. (a) SF, kmin = 1, (b) SF, kmin = 10, (c) ER, p = 0.006, (d) ER, p = 0.1, (e) EXP, kmin = 1, (f) EXP, kmin = 10, (g) SW, knn = 3, pr = 0.03, (h) SW, knn = 3, pr = 0.6, (i) SW, knn = 5, pr = 0.03, (j) SW, knn = 5, pr = 0.6, (k) clustered, knn = 3, pr = 0.001, (l) clustered, pout = 0.1.

For each type of network considered, we find that as the random connections are increased, the localization of Laplacian eigenvectors becomes evident. However, different networks can show different fashions of localization, and we observe mainly two such fashions. Firstly, if there is a wide gap between k_m and k_{m+ 1} or k_{m− 1}, and there is only one node with degree k_m, then f_nm ≈ δ _nm and the localization of Laplacian eigenvectors means

This “ non-degenerate” case is typically encountered in SF and EXP networks when the hub nodes are concerned. Secondly, for the “ degenerate” case in which the spectral gap is narrow and there are many nodes having similar degrees, localization on one single node is unlikely, rather, components of u_m are localized on nodes with degrees close to k_m. That is to say, there is no single f_nm that is close to 1, however, there exist n′ groups such that ∑ _n′ f_{n′ m} ≈ 1 with k_n′ ≈ k_m. Then, one can roughly write that

where χ _{[a, b]}(x) denotes the indicator function, which equals 1 if a ≤ x ≤ b and equals 0 otherwise, and Δ k_m is some threshold that represents the size of the window, in which we consider the degree is close enough to k_m. This is the typical case observed for ER, SW, and clustered networks. We can see that for ER networks, the localization manifests itself on nodes with similar degrees as p is increased. Similarly, for SW networks, as k_nn and p_r are increased, more random connections are introduced, and the localization emerges on nodes with similar degrees. Note the difference between Figs.  8(g) and 8(j). For clustered networks considered in this work with p_out ≈ 0, it is structurally quite distinct that there are N_c = 10 clusters, hence we have λ ₁ = 0 and λ ₂ ≤ · · · ≤ λ _Nc≪ 1. The eigenvectors associated with the smallest N_c eigenvalues are not localized at all, and these small λ , which are characteristics of clustered networks with quite sparse inter-cluster connections, greatly influence the value of Ψ [see Eq.  (3)], leading to the failure of Eq. (1). As p_out is increased, the gap between these N_c − 1 smallest nonzero λ and 0 is also increased, and their influence on Ψ becomes negligible. In addition, for λ > λ _Nc, the localization becomes more distinct as p_out is increased, thus an overall reasonably good localization pattern is observed for clustered networks. Therefore we conclude that the localization of Laplacian eigenvectors becomes evident as the random connections are dense for all types of networks.

We also note that if we let Δ k_m = 0 in Eq.  (8) and there is only one node with degree k_m, then equation  (7) can be recovered by noticing . In this sense, equation  (7) can be considered as a special case of Eq.  (8), although the former is quite accurate when the aforementioned certain conditions are met and the latter contains some ambiguity in the selection of Δ k_m.

Now, we present a qualitative analysis to show why equation  (1) holds. Starting from Eq.  (8) and considering networks in which random connections are dense enough, as a zeroth order approximation, we uniformly distribute components of Laplacian eigenvectors on nodes whose degrees are close to k_m, so

where N_m is the number of nodes whose degrees are close to k_m, and it can be computed as

Inserting Eq.  (9) into the definition of Ψ _i, we have

Note that the nonzero terms on the right-hand side of Eq.  (10) only originate from the case that the degree of node i is close to that of node m. However, if k_i ≈ k_m, then vice versa, say, k_m must be in the neighborhood of k_i, and we intuitively have

which implies

In addition, we further make use of the approximation that for densely connected networks

This approximation is verified by our numerical results in Fig.  8 when the localization of Laplacian eigenvectors is present, and it was also noticed previously for SF and ER networks.^[15] Inserting Eqs.  (11)– (13) into Eq.  (10), we obtain the linear dependence  (6), while for ψ _ij, if it is non-negligible compared to Ψ _i + Ψ _j, then both node i and node j should have similar degrees. For a given k_i, the probability that ψ _ij cannot be omitted is typically as low as . Therefore, in many cases, ψ _ij has little impact on R_{i j}.

Despite the simplifications made in our qualitative theoretical interpretation, we manage to find out a plausible reason why the inequality  (4) and the linear dependence  (6) hold by taking into account the localization property of Laplacian eigenvectors Eq.  (8), based on which equation  (1) can be established. In addition, we do not require any specific topology other than the non-sparseness of networks in our interpretation, therefore we expect that equation  (1) holds for general non-sparse complex random networks.

In this work, we have systematically investigated the two-point resistance R_{i j} of various types of complex networks that are frequently encountered in nature and technology, including scale-free, Erdő s– Ré nyi, exponential, small-world, and clustered networks, and we find a seemingly universal relation [Eq.  (1)], which states that as long as a complex random network is not too sparsely connected, R_{i j} can be effectively estimated by the degrees of node i and node j. Our finding is consistent with that obtained in Ref.  [4] where scale-free and Erdő s– Ré nyi random networks were considered. With the theory established in Ref.  [11], we also provide an explanation to Eq.  (1) by arguing that the underlying mechanism is the localization of Laplacian eigenvectors.^[15] In particular, our analysis is based on the fact that components of the m-th Laplacian eigenvector u_m are typically localized on nodes with degree close to k_m, as observed in all types of networks that are not sparsely connected. (However, a more rigorous theory to explain the finding in this work is still awaited.)

One implication of our work is that provided just a few number of R_{i j} can be measured directly from experiments and only local connectivity information is available, we can compare the estimated values of two-point resistance based on Eq.  (1) and the experimental results. If they are consistent with each other, then the network is possibly non-sparse and the constant C can be fixed, so the two-point resistance of any other two nodes in the network might be further estimated accordingly, as long as their local structural information is available. Also, if the degree of node i is known, and the two-point resistance R_{i j} can be measured, then the degree of node j can be effectively estimated. Furthermore, with Eq. (1), the two-point resistance distribution Φ (R_ij) is naturally obtained as Φ (R_ij) = ∬ P(k_i)P(k_j)δ (R/C − 1/k_i − 1/k_j) dk_idk_j. This can be essentially applied to investigate the transport properties in terms of the statistics of R_{i j} for general non-sparse complex networks other than SF and ER networks as in Ref.  [4].

We consider in this work for simplicity that each link has unit resistance, and there is only one pair of source and sink nodes. However, realistic networks are often weighted and there are multiple sources and sinks.^{[18– 21]} Of particular interest and relevance to water science and petroleum engineering is the case that involves the network model of rock’ s pore space, which is embedded in three-dimensional Euclidean space with the link’ s hydraulic resistance dependent upon its length and cross-sectional area, and the network is typically subject to constant pressure or current condition at two ends. It is our future work to study how the findings here can be used to get insights for transport processes in realistic complex pore networks where the network structure can qualitatively influence the transport process.^{[22, 23]}