Cite this Article
Alqadi M. K.. Stability of magnetic tip/superconductor levitation systems. Chinese Physics B, 24(11): 118404  
Permissions
Stability of magnetic tip/superconductor levitation systems
Alqadi M. K.
Department of Physics, Jordan University of Science and Technology, Irbid, Jordan

†Corresponding author. E-mail: malqadi@just.edu.jo

Abstract

The vertical stability of a magnetic tip over a superconducting material is investigated by using the critical state and the frozen image models. The analytical expressions of the stiffness and the vibration frequency about the equilibrium position are derived in term of the geometrical parameters of the magnet/superconductor system. It is found that the stability of the system depends on the shape of the superconductor as well as its thickness.

Keyword: 84.71.Ba; 74.25.Ha; superconducting ring; magnetic tip; stability; critical state model
1. Introduction

A permanent magnet (PM) flying over a superconductor (SC) is a magnificent feature of superconductors. It has attracted the attention of researchers all over the world due its potential in constructing mechanical systems for various applications such as contactless transportation (maglev), magnetic bearing, and rotor flywheel system. Stability of these mechanical systems is a major concern of engineers who rely on this phenomenon in their constructions.[1, 2] This phenomenon may occur when the superconductor in its Meissner state as well as mixed state. In the Meissner state, the magnet above a finite superconductor could be stable in the vertical direction, while in the horizontal direction, the magnet cannot be stable unless it is placed over a concave superconducting surface. While in the mixed state, the stability is observed in both vertical and horizontal directions, which is attributed to the flux pinning through the high temperature superconducting material.

Various approaches were proposed in the literature to attack the problem of a magnet levitating above a superconductor by introducing different models such as the diamagnetic model, [3– 6] Bean’ s critical state model, [7– 9] and the frozen image model.[10]

Most of the published experimental and theoretical studies were focusing on the possibility of achieving optimal stable levitation of a magnet flying above a superconductor. For example, Davis et al.[11] used Bean’ s model to investigate the stability of a magnet levitated over a large slab of superconductor. Braun et al.[12] measured and calculated the vibration frequencies of a magnet levitated over a high temperature superconductor. Yang et al.[13] calculated the levitation force and vibrations about the equilibrium position for a levitated magnet above a superconducting plane using the image model. Cansiz[14] used the frozen image model to study the vibrations of a magnet above infinite space of a superconducting material. Alzoubi et al.[15] calculated the frequency of vibration in the small magnet/superconducting disk system using the dipole– dipole interaction model. Recently, Del-Valle et al.[16] discussed the vertical and lateral stability in the very long magnetic superconducting bar system using Bean’ s critical model and the energy minimization method.

In this work, we study the dynamical properties, the stiffness, and the vibration frequency of a system consisting of a magnetic tip placed above a superconductor in the critical state. The superconductor is assumed to be very thin with shape of either a ring or a disk. Based on the critical state model, we will derive analytical expressions of the stiffness and the frequency as a function of the dimensional parameters of both the magnet and the superconductor. In addition, we will calculate the stiffness and the frequency of the system by assuming that the tip is placed over a semi-infinite superconductor using the frozen image model.

2. The model

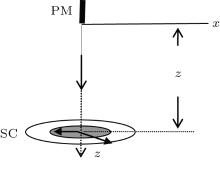
Figure  1 shows the configuration of the system in this study. A magnetic tip of length h levitates a distance z above a superconducting ring of inner radius a, outer radius b, and thickness l. The magnetic wire lies along the symmetry axis of the superconductor, extending from z = − h to z = 0, and it is magnetized along the z direction.

Fig.  1. Schematic diagram of a magnetic tip/superconducting ring system.

The levitation force acting on the magnet above the superconductor arises from the interaction between the induced magnetization and the change in the magnetic field of the tip, which is given by[17]

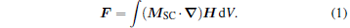Due to the cylindrical symmetry of the present problem, the levitation force has only the vertical component

where the integration is performed over the entire volume of the superconductor. The induced magnetization MSC (dipole moment per unit volume) of the superconductor is defined as[18]

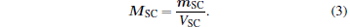The dipole moment of the superconductor is given by mSC = ∫ (r × J)d3r/2, where J is the current flux density within the superconductor.

At any point in space, the magnetic field H generated by the magnetic tip can be calculated using the following equation:

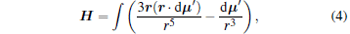where dμ ′ = (MPM/h)dz′ ẑ and r = ρ ρ ̂ + (z − z′ )ẑ .

Based on Bean’ s critical state model, the critical current density Jc through the SC volume is independent of the magnetic field or constant. Therefore, the induced magnetization of the superconducting ring is given by

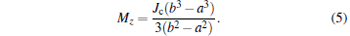The above relation is reduced to Jcb/3 for the superconducting disk.

In the present work, we assume that the superconducting ring is very thin (i.e., the aspect ratio b/L ≫ 1). Therefore, the magnetic energy of the PM/SC system may be expended as

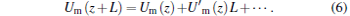The magnetic energy of the magnetic tip and superconducting ring system Ur is given by:

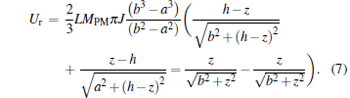If we excite the magnetic tip to make it oscillate about its stable equilibrium position, the total energy of the system U = mgz + Um can be expended as

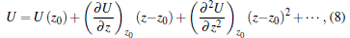where the second term equals zero at equilibrium and (∂ 2U/∂ z2) represents the stiffness of the system (K). Therefore, the stiffness of the magnetic tip and superconducting ring system Kr is given by:

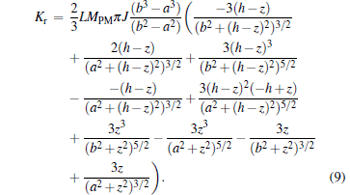Modeling the PM/SC system as a mass/spring system, we may obtain the frequency of the small vertical vibration using the following relation between the frequency and the stiffness:

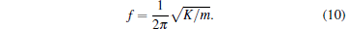The magnetic energy (Ud) and the stiffness (Kd) of the magnetic tip/superconducting disk system are given by

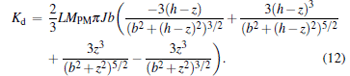In addition to the previous calculations based on Bean’ s critical state model, the frozen image model is used to calculate the stiffness of the system assuming that the magnetic tip levitates above a semi-infinite superconductor at height zo. Based on frozen image model, the total magnetic energy of the system is due to the interaction between the magnetic tip and its frozen image located at − zo and its movable diamagnetic image.[10, 18] The potential energy of the system is given by

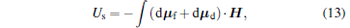where dμ f and dμ d are the magnetic moment elements of the frozen and the diamagnetic images, and H is the magnetic field of the tip. Performing the integral, we obtain the total energy

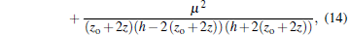The stiffness of the PM/SC system is

3. Results and discussion

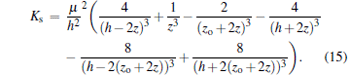The dependence of the stiffness of the PM/SC system on the height of the magnet (z) is shown in Figs.  2– 4. The geometrical and physical parameters of the system are chosen as follows: the inner and the outer radii of the superconducting ring are 0.1  cm and 0.3  cm, respectively, and the thickness L is 0.001  cm; the length and the mass of the magnetic tip are 0.05  cm and 0.1  g, respectively, and its magnetic dipole moment μ equals 0.2  G· m. The critical current density Jc is taken to be 104  A/m2.

Fig.  2. The stiffness of the magnetic tip/superconducting disk system (K) as a function of the levitation height z obtained using the critical state model.

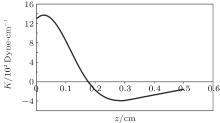Fig.  3. The stiffness of the magnetic tip/superconducting ring system (K) as a function of the levitation height z obtained using the critical state model.

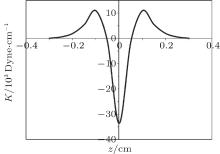
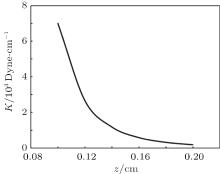Fig.  4. The stiffness of the magnetic tip/semi-infinite superconductor system (K) as a function of the levitation height z obtained using the frozen image model.

Figure  2 shows the variation of the magnetic stiffness of the magnetic tip/superconducting ring system as a function of the height of the tip above the center of the SC ring. It is clear that the stiffness K has a negative value (unstable position) when the height of the magnetic tip above the center of the superconducting ring is less than a certain value, z = 0.05  cm. We may notice that the center of the ring represents the least stable position, while the most stable position is at z = 0.1  cm. Beyond this height, the stiffness is positive but decreases as the height increases.

In Fig.  3, we study the dependence of the stiffness of the magnetic tip/superconducting disk system on the height of the tip above the surface of the SC disk. Contrary to the previous PM/SC ring system, the stability region (K > 0) in this system lies between the surface of the superconducting disk and a certain height z = 0.18  cm, beyond which the magnet is unstable in the vertical direction. The most stable position is slightly above the surface of the SC disk. When the SC is filling half the space, figure  4 shows the calculated stiffness as a function of the height z by using the forzen image model. It is clear that the stiffness is always positive (stable position) and it decreases as the height increases. This trend is in agreement with the experimental trend reported by Cansiz.[11]

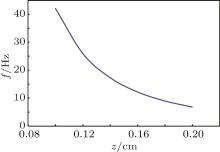
When the magnet is displaced from its equilibrium position, it will oscillate with a frequency f given by Eq.  (10). Figure  5 shows the vibration frequency of the tip above the superconducting ring as a function of the height z. The frequency follows the trend of the stiffness K, therefore, after reaching its maximum value around z = 0.08  cm, the frequency decreases as the height increases.

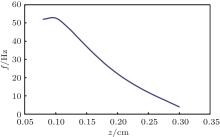Fig.  5. The vibration frequency of the magnetic tip over the SC ring as the function of the height z obtained using the critical state model.

In Fig.  6, it can be seen that when the tip is close to the surface of the supeconducting disk (z < 0.08  cm), the vibration frequency is almost independent of the height z. If z > 0.08  cm, the frequency drops rapidly as the height increases. It should be noted that in the case of thin superconducting films, both experimental[19] and theoretical studies[9] reported that the maximum force between the magnet and the thin superconductor occurs above the surface of the superconductor rather than on its surface. Our present study is in agreement with the reported results[9] in the sense that the position of the maximum stiffness and frequency is located above the surface of the superconductor. The variation of the vibration frequency of the magnetic tip with the distance between the tip and the semi-infinite superconductor is presented in Fig.  7. It is clear that the frequency of the tip decreses as the height z increases.

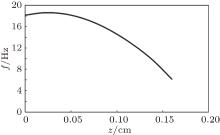Fig.  6. The vibration frequency of the magnetic tip over the SC disk as the function of the height z obtained using the critical state model.

Fig.  7. The vibration frequency of the magnetic tip over the semi-infinite superconductor as the function of the height z obtained using the frozen image model.

4. Conclusion

The stiffness of the magnetic tip and superconducting ring (disk) system as well as the vibration frequency were calculated using the critical state model and the frozen image model. The analytical expressions of the stiffness and the frequency of vibration about the equilibrium position as a function of the geometrical parameters of the system were derived. For the thin superconducting disk or ring, the position of the maximum stability is at a distance from the surface of the superconductor.

Reference
1 Wang Q L 2013 Practical Design of Magnetostatic Structure using Numerical Methods New York Wiley [Cited within:1]
2 Liu J, Wang Q L and Li X 2010 IEEE Trans. Appl. Supercond. 20 47 DOI:10.1109/TASC.2009.2038361 [Cited within:1]
3 Badia and Freyhardt H C 1998 J. Appl. Phys. 83 2681 DOI:10.1063/1.367032 [Cited within:1]
4 Lugo J and Sosa V 1999 Physica C 324 9 DOI:10.1016/S0921-4534(99)00466-9 [Cited within:1]
5 Perez-Diaz J L, Garcia-Prada J C and Diaz-Garcia J A 2009 Physica C 469 252 DOI:10.1016/j.physc.2009.02.004 [Cited within:1]
6 Alqadi M K, Alzoubi F Y, Saadeh S M, Al-Khateeb H and Ayoub N Y 2012 J. Supercond. Nov. Mag. 25 1469 DOI:10.1007/s10948-012-1483-7 [Cited within:1]
7 Bean C P 1962 Phys. Rev. Lett. 8 250 DOI:10.1103/PhysRevLett.8.250 [Cited within:1]
8 Brand t E H 1989 Science 243 349 DOI:10.1126/science.243.4889.349 [Cited within:1]
9 Sanchez A and Navau C 1996 Physica C 268 46 DOI:10.1016/0921-4534(96)00400-5 [Cited within:3]
10 Kordyuk A A 1998 J. Appl. Phys. 83 610 DOI:10.1063/1.366648 [Cited within:2]
11 Davis L C, Logothetis E M and Soltis R E 1988 J. Appl. Phys. 64 4212 DOI:10.1063/1.341312 [Cited within:2]
12 Braun M, Buszka P, Motylewski T, Przydrozny W and Sliwa C 1990 Physica C 171 537 DOI:10.1016/0921-4534(90)90269-K [Cited within:1]
13 Yang Z Y, Johansen T H, Bratsberg H, Helgesen G and Skjeltorp A T 1989 Physica C 160 461 DOI:10.1016/0921-4534(89)90421-8 [Cited within:1]
14 Cansiz A 2003 Physica C 390 356 DOI:10.1016/S0921-4534(03)00785-8 [Cited within:1]
15 Alzoubi F Y, Al-Khateeb H M, Alqadi M and Ayoub N Y 2006 Chin. Phys. Lett. 23 164 [Cited within:1]
16 Del-Valle N, Sanchez A, Navau and Chen 2008 Supercond. Sci. Technol. 21 125008 DOI:10.1088/0953-2048/21/12/125008 [Cited within:1]
17 He C and Wang Q L 2007 Cryogenics 47 413 DOI:10.1016/j.cryogenics.2007.04.007 [Cited within:1]
18 Alqadi M K, Alzoubi F Y, Al-Khateeb H and Ayoub N Y 2009 Physica B 25 1781 DOI:10.1016/j.physb.2009.02.019 [Cited within:2]
19 Riise A B, Johansen T H, Bratsberg H, Kobliscka M and Shen Y Q 1999 Phys. Rev. B 60 9855 DOI:10.1103/PhysRevB.60.9855 [Cited within:1]