In the millimeter and sub-millimeter wavelength band, reflectors based on the Bragg coupling of counter-propagating waves in the periodic structures can provide a frequency selective feedback for overmoded high-power oscillators such as the cyclotron auto-resonance maser (CARM), ^{[1– 3]} free electron laser (FEL), ^[4] gyrotron backward wave oscillator (BWO), ^[5] and terahertz (THz) BWO.^[6] The periodically corrugated waveguides composed of the reflector can provide a high reflectivity through the principle of constructive interference, allowing the formation of a frequency selective resonator with effective electron beam transportation. A forward wave is coherently scattered into a reflected wave due to the cascaded corrugations. Superposition of multi-waves leads to a high reflectivity when the Bragg resonant condition (k_b = 2k, k is the axial propagation constant, k_b = 2π /d, and d is the corrugation period) is satisfied.

For a BWO or gyro-BWO, ^{[5– 7]} the oscillation signal will be collected in the upstream end on the gun side due to the properties of the backward wave. Thus, an energy extracting system must be connected between the high-frequency slow wave structure (SWS) and the electron gun, which increases the structural complexity in the design and fabrication. One solution to this issue is to reflect the output power to the downstream end near the collector by using a Bragg reflector and then radiate it from an axially aligned horn. Like the BWO’ s coupling system, an input coupler for travelling wave tubes (TWTs)^[8] comprised of the Bragg reflector can achieve a relatively large beam tunnel and broad bandwidth compared to the coupler with a cutoff waveguide. This structure also allows electrons to have good transportation and the path to be unobstructed. The corrugated reflector herein under discussion is very promising for realizing the compact size and miniaturizing the sheet beam BWOs or TWTs in the THz range.

Generally, a corrugated Bragg resonator with a cylindrical cross section^{[1, 2, 4, 5]} or coaxial structure^{[3, 9]} is adopted in the CARM, FEL, and gyro-BWO. However, a sheet electron beam promotes the development of 2D radiation sources, ^{[10– 12]} where a planar Bragg reflector comprised of the symmetric periodic corrugations is of great importance for their design. A tunable planar narrow-band advanced Bragg reflector (ABR) based on the interaction between a propagating wave and a quasi-cutoff trapped wave is proposed by Ginzburg et al.^{[13, 14]} However, the propagating mode injected into the reflector must be in the TEM mode, which is usually not consistent with the stimulated mode in the BWO or TWT. Furthermore, the ABR width of the overmoded corrugated waveguide is very large so that high order modes may be excited. Therefore, a planar conventional Bragg reflector is considered instead of the ABR. In this paper, a planar corrugated Bragg reflector for the sub-terahertz (0.18– 0.22  THz) BWO operation is demonstrated. The rest of this paper is organized as follows. In Section  2, the multi-mode coupling analysis is presented. Coupling equations of the mathematical and physical basis are derived. The formulation is similar to that for the cylindrical cross-section, and relevant reflector performances including the reflection, transmission rate and the coupling coefficients are updated by using the multi-mode coupling theory (MCT). In Section  3, an operating mode TE₁₀ and a dominant coupling mode TE₀₁ are considered. Numerical results obtained by the MCT and CST Microwave Studio (CST-MWS) are compared and their good agreement is achieved. Besides, performance based on different structural parameters is analyzed in detail and discussed, which can instruct our optimization, fabrication, and measurement in the next stage. In Section  4, conclusions are drawn from the present study.

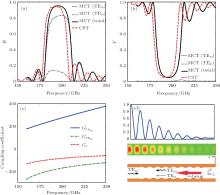
Figure  1(a) shows the diagram of the BWO. In order to reflect the BWO output signal to the downstream end and then radiate it by a launching horn, a reflector comprised of corrugated waveguides is designed. Three-dimensional (3D) modeling and basic geometry of the planar Bragg reflector are configured in Figs.  1(b) and 1(c), where the right-hand side (RHS) of the reflector connects with the planar electron gun (E-gun) and the left-hand side (LHS) connects with the BWO SWS. In this figure, A⁺ and A⁻ , respectively, represent the forward and coupling backward wave, while A(z) denotes the exponentially decaying reflectivity or transmission rate. A⁺ is generated by the beam-wave interaction in the BWO SWS, and then propagates towards the upstream end of the BWO due to the property of the backward wave. In the reflector, A⁻ is also excited due to the corrugated waveguide. Note that A⁻ is reflected to the SWS and then overlaps with A⁺ when the Bragg resonant condition k_b = 2k is satisfied, where 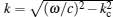, and k_c is the cutoff wavenumber. Here we assume that the waveguide wall has a weak plane symmetric sinusoidal corrugation: a(z) = a₀ + a₁ cos (k_bz), where a₀ is the mean distance between the two corrugation plates and a₁ is the ripple amplitude. The corrugation period, width, and total longitudinal length are d, w, and l, respectively.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Backward wave oscillator with Bragg reflector. refer to the Bragg reflector, slowing wave structures, radiation horn, and output window, respectively. (b) 3D modeling. (c) Schematic diagram of the planar Bragg reflector.

The coupled mode equations between A⁺ and A⁻ can be described as^{[2, 13]}

Here, Bragg mismatch Δ = k − k_b/2, α is the Ohmic dissipation loss constant (in the following discussion, we omit the influence from this item), and G is the wave coupling coefficient. Corrugations can couple one mode i to another mode j in the cavity if they satisfy the modified Bragg resonant condition

The multi-mode coupling equation is

where G_ii, G_{j j}, and G_{i j} represent the self-coupling and cross-coupling coefficients of mode i and j, respectively. Let mode i represent a TE mode (H-mode) and mode j represent a TM mode (E-mode), then general equations will be extended to four first-order linear equations expressed in a vector form as

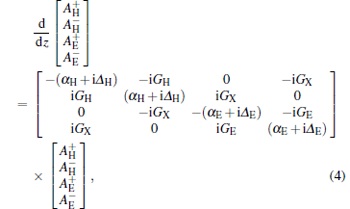where Δ _H and Δ _E are the Bragg mismatch factors of the TE and TM mode; G_H, G_E, and G_X are the self-coupling coefficients of TE– TE and TM– TM, and cross-coupling coefficient of TE– TM, respectively.^{[2, 15]}

For a planar Bragg reflector with the consistent corrugation width discussed in this paper, the general coupling coefficients are given by^[16]

where

The indices i and j are for the coupling modes TE_mn (TM_mn) and TE_{m′ n′} (TM_{m′ n′} ), respectively. In these equations, ɛ _p = 1 when p ≠ 0 and ɛ _p = 2 when p = 0. G_E, G_H, and G_X are related to the geometry a₀, a₁, w, and mode indices. If the Bragg reflector operates in a single mode, the coupling coefficients of the second self-coupling and cross-coupling items in Eq.  (5) will be 0, i.e., G_E = 0 and G_X = 0.

The field amplitude in the waveguide satisfies A ∝ e^{λ z}, then equation  (4) can be described as a compact matrix eigenvalue problem given by

Here, matrix M is the first vector item on the RHS of Eq.  (4); λ and e are its eigenvalues and eigenvectors, respectively; I is an identity matrix. Once the eigenvalues and eigenvectors are found, the amplitude vector A at any position in the reflector can be expressed as a linear combination of four eigenvectors

where K_i is a constant satisfying the boundary condition. Boundaries at the reflector ends (z = 0 and z = l) for TE (TM) mode are

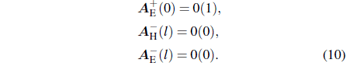Using the values of K_i solved by Eqs.  (9) and (10), the total reflection coefficient R and total transmission coefficient T can be obtained by the combination of H- and E-mode (or H- and H-mode or E- and E-mode)

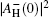
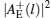
where and are the reflected power of H- and E-modes at z = 0, and similarly and are the corresponding transmission power at z = l, where z = 0 and z = l are the entrance (towards the SWS) and exit (towards the electron gun) of the Bragg reflector shown in Fig.  1.

For our sub-terahertz BWO central frequency at 0.2  THz, the designed SWS width is 1.2  mm. For simplicity, the reflector corrugation width w is also chosen as the same dimension. To make sure that the e-beam emitting from the E-gun will not be pre-bunched in the Bragg reflector and the circuit length is not too long, the mean distance between the Bragg gratings is around the dimension of the width. Considering the incident wave TE₁₀ mode determined by the BWO, odd high-order modes, such as TE₃₀ and TE₅₀, are not easy to generate because of the constant corrugation width. However, degenerated wave pairs TE₁₀/TE₀₁ may be produced because the constant width and mean distance of the gratings are very close to each other. For our square-like overmoded corrugated waveguide with weak ripples, the 1st– 2nd parasitic waves are TE₀₁, TE₁₁(TM₁₁), and TE₂₀. Two dominant modes TE₁₀ and TE₀₁ in the cavity controlling the reflector performance will be mainly discussed by using MCT in the following sections. With parameters of d = 1.0  mm, w = 1.2  mm, and a₀ = 1.1  mm, the Bragg resonance criteria k_TE10 + k_TE01, k_TE10 + k_TE(TM)11, k_TE10 + k_TE20, and k_b for the fundamental TE₁₀ and another coupling mode are plotted in Fig.  2. Optimal Bragg resonant points are at 0.20  THz, 0.22  THz, and 0.26  THz, respectively.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Bragg resonance criteria for two modes of TE10 and TE01, TE20 and TE11 (TM11), where kb is the Bragg resonant condition.

Table  1 shows a group of optimized parameters for the Bragg reflector working in a sub-terahertz band centered at 0.2  THz. Reflection, transmission performance, and self- and cross-coupling coefficients of the TE₁₀, TE₀₁, and the total combination rate obtained from MCT are demonstrated in Figs.  3(a)– 3(c). The total reflection and transmission rate obtained by CST-MWS^[17] are also compared in the figures. Figure  3(d) also shows the total power contour plot and its normalized power flow. We can obverse that a maximum of 13.7% TE₀₁ around 0.19  THz is coupled and reflected to the entrance. Total reflectivity and transmission are 0.95 and 0.05, respectively. The 3-dB bandwidths from the MCT scheme and CST-MWS are 28  GHz (0.183– 0.211  THz) and 26  GHz (0.180– 0.206  THz), respectively. The operating band obtained by MCT is 1%− 2% higher than that from CST-MWS, which is because in our theoretical analysis only the operating mode TE₁₀ and a dominant coupling mode TE₀₁ are included, but much higher-order modes are neglected. From our simulation, we find the suppression to the nearest higher-order modes except the TE₀₁ is maintained at a very high level (> 130  dB). We can also find that the self-coupling coefficient G_TE10 increases, but the self-coupling coefficient G_TE01 and cross-coupling coefficient G_X decrease with the band extending to higher frequencies. This reveals that the reflectivity in the reflector is mainly controlled by the TE₁₀ mode, and this effect is enhanced with the increase of frequency.

Table 1.

Table 1.

Table 1. Typical operating parameters of the Bragg reflector. Corrugation period d 1.0  mm Corrugation amplitude a1 0.1  mm Corrugation width w 1.2  mm Mean distance a0 1.2  mm Reflector length l 8.0  mm Center frequency ω /ω c 1.60

Table 1. Typical operating parameters of the Bragg reflector.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Numerical results calculated by MCT and CST-MWS: (a) reflectivity and (b) transmission of TE10, TE01, and their combination, (c) self-coupling and cross-coupling coefficients as a function of frequencies, and (d) power distribution function and contour plot along the axial distance at 0.2  THz.

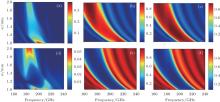
From our previous discussion and Eqs.  (5)– (7), coupling coefficients are determined by the mode indices, corrugation width w, corrugation amplitude a₁, and mean distance a₀. Therefore, only the coupling coefficients relative to a₁, a₀, and w are studied in the following sections. The dependences of reflectivity, transmission, and coupling coefficients on various parameters can instruct the design, modelling, fabrication, and final tolerance assembled with our BWO slow wave structure. Figure  4 gives the reflection and transmission rates of TE₁₀, TE₀₁, and the total combination, respectively, in Figs.  4(a)– 4(f), each of which is a function of the operating frequency and a₀/a₁. Our investigation indicates the reflector performances studied here, resulting from a₀ and 1/a₁, have the same variation tendencies, thus we define a normalized factor a₀/a₁ to illustrate this situation. There are two different cases, i.e., the increasing a₀ and reducing a₁, resulting in the increase of a₀/a₁. For the former case, the increasing a₀ leads to overmoded characteristics of the corrugated waveguide so that the TE₀₁ mode is much easier to excite. Both of these cases form a relatively weak ripple amplitude, which could reduce the reflectivity and bandwidth. When increasing a₀, the influence from the corrugations will be weakened and the corrugated waveguide evolves into a smooth waveguide, where TE₁₀ has a very low conversion and couples with higher-order modes so that the reflector performance worsens. Figure  5 shows the relevant coupling coefficients, and one can see that the magnitudes of these coefficients reduce until they are close to zero with increasing a₀/a₁. This phenomenon is consistent with the scenarios in Figs.  4(c) and 4(f). For the distance a₀ between the two corrugations, if it is too small, the beam cross section will be limited; however, if it is too large, the confined PPM will not have enough space. From these two figures, we can also know whether the BWO is updated to a wide band operation, and reducing a₀ or increasing a₁ can improve the bandwidth of the matching Bragg reflector.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Reflectivities and transmissions each as a function of frequency and normalized parameter a0/a1. (a)– (c) Reflectivities of TE01, TE10, and the total combination; and (d)– (f) transmissions of TE01, TE10, and the total combination.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) Self-coupling coefficient GTE10, (b) self-coupling coefficient GTE01, and (c) cross-coupling coefficient GX versus frequency and a0/a1.

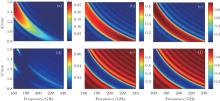
Figures  6 and 7, respectively, demonstrate the reflectivity, transmission rate, and coupling coefficients versus corrugation width w in the operating frequency range. When broadening w, operating bands of TE₀₁, TE₁₀, and their combination will shift to lower frequencies and meanwhile the bandwidth is greatly extended. This is because the increasing waveguide width results in a lower cutoff frequency. Note that in Figs.  6(a) and 6(d), reflection and transmission amplitudes of TE₀₁ each have a concave region from w = 1.1  mm to 1.5  mm. Similar overmoded characteristics with the changing a₀/a₁ mentioned above occur here when changing w. Besides, the self-coupling coefficient G_TE10 of TE₁₀– TE₁₀ increases, and G_TE01 of TE₀₁– TE₀₁ remains unchanged, whereas cross-coupling coefficient G_X between TE₁₀– TE₀₁ decreases. The sensitivity of the width to the reflector performance indicates that it is much easier to shift the operating band by adjusting w, but the problem is that the beam tunnel will be seriously affected.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Reflectivities and transmissions versus corrugation width w. (a)– (c) Reflectivities of TE01, TE10, and the total combination; and (d)– (f) transmissions of TE01, TE10, and the total combination.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. (a) GTE10 for TE10– TE10, (b) GTE01 for TE01– TE01; and (c) GX for TE10– TE01 versus frequency and w.

Figures  8 and 9 demonstrate the reflectivities and transmissions each as a function of corrugation period d and normalized reflector length l/d, respectively. The reflectivity (Fig.  8(a)) of TE₀₁ increases up to 0.25 when extending the corrugation period to d = 1.5  mm, but the stop-band center is changed to 0.16  THz. Compared with the reflectivity, its transmission (Fig.  8(d)) in this case still stays at a very low level (less than 0.06). For the combined total reflection and transmission rate shown in Figs.  8(c) and 8(f), the whole operating range also shifts to lower frequencies with increasing d, accompanied by reducing the absolute bandwidth. In Fig.  9, the reflectivities of TE₀₁ and TE₁₀, respectively, concentrate in the lower and upper bands of the working range and the maximum proportions are ∼ 15% and 85%. Unlike the reflectivity, the proportion of TE₀₁ contributing to the total transmission rate is very low in the stop band, and an interesting thing is that the maximum value (∼ 10%) emerges in the first side lobe but not the center. For the total reflectivity and transmission given in Figs.  9(c) and 9(f), the filtering stop bandwidth (0.18– 0.22  THz) does not change except for the magnitude. If we want to make sure that the reflectivity is over 0.95, the length of the reflector must be over 10 periodical Bragg corrugations. This conclusion can make us find the shortest reflector length so that the dimension of the whole BWO circuit is more compact in the engineering.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. Reflection and transmission rates each as a function of frequency and corrugation period d. (a)– (c) Reflectivities of TE01, TE10, and the total combination; and (d)– (f) transmissions of TE01, TE10, and the total combination.

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. Reflectivities and transmissions versus frequency and normalized reflector length l/d. (a)– (c) Reflectivities of TE01, TE10, and the total combination; and (d)– (f) transmissions of TE01, TE10, and the total combination.

Multi-mode coupling theory is derived and used to analyze a sub-terahertz wavelength (0.18– 0.22  THz) planar Bragg reflector, which is comprised of a periodical corrugated waveguide. It can benefit the compact design of sheet beam BWO or TWT as a promising component. A dominant mode TE₁₀ and main coupling mode TE₀₁ are considered in the MCT analysis. The reflector performance including reflectivity, transmission rate, and coupling coefficients calculated from MCT is examined and compared with the results obtained by CST– MWS, and good agreement is achieved. The influence of the structural dimension on reflector performance is demonstrated, which can instruct our final fabrication and assembly. The increases of a₀/a₁ and the number of Bragg cavities have no effect on the central frequency, but have great influences on the bandwidth and amplitude. Increasing the reflector width and period length would reduce the operating frequency. The bandwidth of the former case is extended, but the bandwidth of the latter one remains nearly unchanged.