†Corresponding author. E-mail: zanli@xidian.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 61301179), the Doctorial Programs Foundation of the Ministry of Education, China (Grant No. 20110203110011), and the Programme of Introducing Talents of Discipline to Universities, China (Grant No. B08038).
A data-aided technique for carrier frequency offset estimation with continuous phase modulation (CPM) in burst-mode transmission is presented. The proposed technique first exploits a special pilot sequence, or training sequence, to form a sinusoidal waveform. Then, an improved dichotomous search frequency offset estimator is introduced to determine the frequency offset using the sinusoid. Theoretical analysis and simulation results indicate that our estimator is noteworthy in the following aspects. First, the estimator can operate independently of timing recovery. Second, it has relatively low outlier, i.e., the minimum signal-to-noise ratio (SNR) required to guarantee estimation accuracy. Finally, the most important property is that our estimator is complexity-reduced compared to the existing dichotomous search methods: it eliminates the need for fast Fourier transform (FFT) and modulation removal, and exhibits faster convergence rate without accuracy degradation.
Continuous phase modulation (CPM) has attracted much attention in recent years for its high power and spectral efficiency, and its constant signal envelope can significantly alleviate the nonlinear effects of high power amplifiers.[1] The CPM has been widely used in satellite communications and terrestrial mobile cellular systems, [2– 6] etc. However, achieving good performance relies on precise synchronization, especially with low signal-to-noise ratios (SNRs). Thus, estimators that provide good performance and low complexity are of significant interest.
To perform synchronization, symbol timing and carrier information must be taken into consideration. Both frequency offset and phase offset estimation should be performed as part of carrier synchronization. In this study, we focused only on frequency offset estimation with CPM signals, and in subsequent analysis it was found that our estimation method is independent of timing recovery. Many researchers have proposed algorithms for frequency offset estimation.[7– 21] In Refs. [7]– [17], traditional phase-locked loop schemes are presented, which employ a feedback structure to track the precise value of the frequency offset, but such approaches require long periods of time for acquisition, and thus, they may not be feasible with burst-mode transmission. In Refs. [10] and [11], a maximum-likelihood algorithm, the most fundamental feedforward structure, is presented for searching the frequency offset by compensating for a set of discrete points and maximizing the log-likelihood function (LLF). However, the true frequency offset point may be missed if it lies between two searching values. To avoid this situation, numerous discrete points must be used, leading to unacceptable complexity. Some other estimation methods, such as those discussed in Refs. [12]– [14], estimate frequency offset by operating on the correlation values of the modulated signals. These approaches require high computational resources. Subsequent proposed feedforward estimation methods[15– 17] are variations on the classical methods described above; they reduce the complexity to some extent, however, the level of complexity is still undesirable. In 1999, a dichotomous search frequency offset estimator was proposed by Zakharov and Tozer.[18] This was the first time that a one-dimensional optimization search method was introduced into frequency offset estimation. This type of estimator seeks the optimum point through an iterative algorithm. Several years later, Aboutanios presented a modified dichotomous search estimator in which the initializations of the iterative algorithm are computed in a more reasonable manner.[19] Both estimators operate in the frequency domain, meaning that a fast Fourier transform (FFT) must be carried out. To ensure the accuracy of the two types of dichotomous estimators, the order of the FFT operation must be larger than 1.5 times the number of signal points.[18– 20] Subsequently, other similar estimators, such as Gaussian spectrum interpolation, parabolic interpolation, and weighted multipoint interpolation, were introduced to improve the resolution of the FFT frequency measurement.[21] However, with these methods, practical implementation still involves unsatisfactory levels of complexity.
In this paper, we present a special pilot sequence and an improved dichotomous search frequency offset estimator that can reduce the complexity of the overall system. The proposed estimator first exploits the special pilot sequence, or training sequence, to form a sinusoidal waveform whose frequency information can be easily extracted and which requires no modulation removal. Then, the improved dichotomous search method is introduced to obtain the frequency offset estimation. All these procedures are performed in the time domain, and thus the FFT operation is eliminated. Analysis indicates that our estimator is suitable for nearly all CPM formats since it imposes no restrictions on alphabet and modulation index, except that the modulation index is rational. Analysis and simulation results demonstrate that our estimator exhibits lower complexity without accuracy degradation compared to the existing methods presented in Refs. [18] and [19].
This paper is organized as follows: Section 2 provides a brief introduction to the burst-mode transmission model and the derivation of LLF with CPM. Section 3 provides the background information related to the traditional dichotomous search method. In Section 4, our improved dichotomous search estimator is described in detail. Simulation results are presented in Section 5 to demonstrate the benefits of our proposed method, and the paper is concluded in Section 6.
In burst-mode transmission, the modulated signal is transmitted in bursts in a deterministic manner that is known by the receiver. The transmission structure is depicted in Fig. 1. Each burst consists of three parts. The first part is the known pilot sequence used to perform parameter estimation. The next part is the unique word (UW), which is utilized to identify the bursts. The last part, referred to as the payload, transmits the unknown source information.
It is assumed that the CPM signal is transmitted according to a burst-mode model. The complex baseband CPM signal during the transmission of each burst can be expressed as
 |
where Es denotes the energy per transmitted symbol, T is the symbol period, and ψ (t, α ) is the phase function expressed as follows:
 |
Here, h is the rational modulation index, and α i is the data sequence transmitted up to time nT. The data symbols are independent, equally likely sequences belonging to the M – ary bipolar alphabet {± 1, ± 3, … , ± (M − 1)}. The phase response pulse q(t) is a continuous, monotonic function defined as follows:
 |
The frequency response pulse g(t) = dq(t)/dt is nonzero over the interval [0, LT], where L is the correlation length. The schemes most commonly used for g(t) are L-rectangular frequency pulse (LREC), L-raised cosine pulse (LRC), and L-interval Gaussian-minimum shift keying pulse (L-GMSK). The corresponding mathematical expressions are listed in Table 1. In the Appendix A, we demonstrate that the LLF has the same expression for all of these frequency response pulses, and this indicates that our algorithm is suitable for most types of CPM signals.
| Table 1. Commonly used schemes for g(t). |
In Table 1, B represents the − 3 dB bandwidth of the Gaussian pulse shape, and Q(x) is the Q-function expressed as follows:
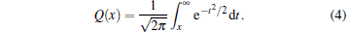 |
The received signal has the form
 |
where
 |
In Eqs. (5) and (6), v, τ , and φ are the frequency offset, the timing delay, and the channel phase, respectively. Both τ ∈ (− T/2, T/2) and φ ∈ (− π , π ) obey uniform distribution, w(t) is a zero-mean complex white Gaussian noise term with two-sided power spectral density N0/2. In Eq. (6), the signal component s(t) is a function of time combined with a set of parameters γ . This set can consist of v, τ , φ , and data symbols; however, it does not necessarily contain all of them at once. In our system, the data symbols are known and are not included in γ because a training sequence is transmitted; thus, only v, τ , and φ are included. To emphasize the dependence of the signal on unknown parameters, we adopt the notation s(t, γ ) in place of s(t) and rewrite Eq. (5) as
 |
If we assume that γ ̃ is a hypothetical value set of γ , the joint LLF for the synchronization parameters takes the following form:[9]
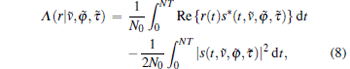 |
where N is the length of the pilot sequence and Re is the real operator. CPM has a constant envelope, and thus the second term in Eq. (8) becomes a constant and can be omitted for convenience. It is shown in the appendix that sCE(t) is a sinusoidal waveform with frequency f1 = h/(2T) if an all-one training sequence is transmitted. Suppose the initial phase of the sinusoidal waveform is θ , which is deterministic for a given CPM format, and sCE(t) can be rewritten as
 |
Substituting Eq. (9) into Eq. (8) and ignoring the immaterial factor, we can obtain
 |
where φ ̃ 1 = − 2π f1τ ̃ + φ ̃ + θ is a joint phase related to τ ̃ , φ ̃ , and θ .
The parameters are decoupled now, and thus the maximization of the LLF becomes straightforward. The term that corresponds to the frequency offset in Eq. (10) is defined as
 |
and thus, maximizing the LLF is equivalent to maximizing the objective function
 |
Discrete-time estimation can be accomplished by sampling the continuous-time function. The number of samples per symbol interval is denoted by Ns, and the discrete-time format of Eq. (12) can be written as
 |
where the parameters ṽ and f1 in Eq. (13) have been normalized to the symbol interval.
From Eqs. (10)– (13) it is clear that parameter τ ̃ can be incorporated into the joint phase φ ̃ 1 and does not appear in the objective function; therefore, our algorithm for frequency offset estimation is independent of timing recovery. Furthermore, because the objective function has the form of a sinusoid, the operation of modulation removal can be bypassed. This represents one aspect of the reduced complexity provided by our estimator. In Section 4, this property will be discussed in detail.
To provide supporting information for our later analysis, a brief introduction to the dichotomous and modified dichotomous search frequency offset estimator is presented; readers who are interested in a more detailed discussion can refer to Refs. [18] and [19]. This estimator first obtains the maximum bin of a K-point FFT, then a dichotomous (or modified dichotomous) search method is used to derive the true frequency offset value. The index of the maximum bin is denoted by m, and the procedure of the algorithm is summarized below.
Step 1 Perform modulation removal to obtain a sinusoid as

Step 2 Let K = lNNs, then calculate S = FFT(x, K) and Y = | S(n)| 2.
Step 3 Find 
Step 4 (i) For dichotomous search method, set Δ = 1, Y− 1 = Y(m − 1), Y0 = Y(m), and Y1 = Y(m + 1). (ii) For modified dichotomous search method, set Δ = 0.75, Y− 1 = Y(m − 1), Y0 = Y(m), and Y1 = Y(m + 1). If Y1 > Y− 1, then

else

Step 5 For Q iterations do

If Y1 > Y− 1, then

else

Update such that

Step 6 Obtain the normalized frequency offset value
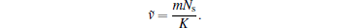
The dichotomous search frequency offset estimator was first proposed by Zakharov and Tozer.[18] A binary search method is used to locate the true FFT peak (Steps 1– 3), then the FFT coefficients on both sides of the maximum are compared to halve the frequency resolution (Step 4). The procedure is repeated for Q iterations in order to ensure the accuracy of the estimation (Step 5). Later, Aboutanios modified the method simply by making it possible to calculate the initialization of the iterations more reasonably. However, to ensure that the variance of the estimator achieves the Cramer– Rao bound (CRB), l ≥ 1.5 and Q ≥ 10 are necessary, and this leads to high computational load. We will now present an improved algorithm that reduces the complexity of the dichotomous search method. For the sake of brevity in the forthcoming comparisons, we will refer to the conventional method as FFT & dichotomous and our proposed method as improved dichotomous.
To clarify the relationship between our algorithm and the conventional algorithms described in the previous section, we will use the same format when presenting the procedure of our improved estimator. To begin with, an initialized range must be given for use in subsequent processing. We specify the range as (v− 1 , v1) with v− 1 < v1.
Step 1 Initialize the search range (v− 1 , v1).
Step 2 Calculate Y− 1 = f (v− 1) and Y1 = f (v1) using Eq. (13).
Step 3 For Q iterations, do

If Y− 1 < Y1, then

else

Step 4 Obtain the normalized frequency offset value

If our estimator is compared to the conventional estimators described in Section 3, it is clear that the complexity is greatly reduced owing to the elimination of modulation removal and FFT operations. However, the reduced complexity is achieved at the expense of a small estimation range. Based on one-dimensional optimization search theory, the dichotomous search method is available only if the objective function is unimodal; [22, 23] thus, the estimation range is confined to the unimodal interval of the objective function. Substituting Eqs. (5) and (6) into Eq. (12) and rearranging the expression, eventually we obtain
 |
where w̃ (t) is Gaussian noise. If the noise term is ignored, the objective function can be simplified as
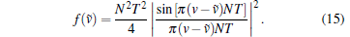 |
The objective function reaches the maximum at ṽ = v. However, because the noise is always present, the maximum bin is more accurately written as ṽ = v + vw, where vw is a random term representing the noise. Thus, we have
 |
where E represents the expectation operator. Equation (16) suggests that our estimator is unbiased. In Section 5, the simulation results will be presented to corroborate this conclusion.
The curve of the normalized objective function is shown in Fig. 2; based on this curve, we know that in order to ensure the unimodality of the function, the estimation range must be confined to the main lobe, that is
 |
From Eq. (17), it is clear that the estimation range is small compared to that of the FFT & dichotomous method, whose estimation range is (− 1/2T, 1/2T). However, this is a desirable trade-off because in most cases the residual offset is much smaller than ± 1/2T.
This section presents a series of simulations that were conducted to verify the benefits of our proposed algorithm. The parameters are configured as follows: the length of the pilot sequence is N = 16, the symbol rate is 1 MHz, and the number of samples during one symbol interval is Ns = 8, henceforth, the sample rate becomes 8 MHz.
Figure 3 presents the real parts of the modulated all-one sequence waveforms, all of which are sinusoidal and satisfy f1T = h/2. These waveforms exhibit different frequency pulses, different correlation values, different modulation indices, and, for L-GMSK, different − 3 dB bandwidths. They may exhibit variations in the initial phases, but this will not have any effect on our frequency offset estimation because the phase θ is incorporated into the joint phase φ ̃ 1 (see Eq. (10)). In our later simulations presented in Section 5.2, g(t) = 2RC and h = 1/4 are used, and the same simulation results can be obtained for any other set of parameters.
Figure 4 presents the average estimation versus the normalized frequency offset at Es/N0 = 8 dB. Because the length of the pilot sequence is N = 16, the maximum frequency offset should be less than about 6% of the symbol rate. As is evident in the figure, the simulation results agree well with our theoretical analysis. Furthermore, in the range confined according to Eq. (17), the average simulation results coincide with the true frequency offset values, confirming that our estimator is unbiased.
Figure 5 presents the normalized frequency offsets versus Es/N0 during different iterations for both the FFT & dichotomous search method and our improved dichotomous search method. The CRB (see Eq. (18)) is also shown in the figure as a lower limit of the variances. Here, the FFT & dichotomous approach uses the modified search method proposed by Aboutanios.[19] To clarify the relative characteristics of the two estimators, we present in Table 2 a comparison of their performance and complexity
 |
 | Fig. 5. Normalized frequency offset variance versus Es/N0. (a) FFT & dichotomous search, (b) improved dichotomous search. |
As shown in Fig. 5(a) for the FFT & dichotomous search method, the signals must be padded with zeros to coincide with the CRB, and the number of padded zeros must be at least half of the length of the signals, i.e., l ≥ 1.5. However, in a practical hardware design, l = 2 is required for FFT operation, leading to high computational load. Our improved estimator alleviates this computational burden by eliminating the FFT operation, thereby reducing the need for processing and memory components in the hardware design. As stated in Table 2, the FFT & dichotomous search requires 10 iterations to achieve the CRB, whereas our improved dichotomous search method needs only 6. This faster convergence rate represents another aspect in which the complexity of our estimator is significantly reduced. In addition, our proposed method exhibits Es/N0 threshold below − 10 dB, whereas that of the conventional method is 2 dB. Another advantage of the improved dichotomous method over the FFT & dichotomous method is that the former requires no timing information. Owing to this property, our algorithm can be applied even in the absence of accurate timing synchronization, and is thus compatible with simpler hardware designs.
| Table 2. Comparisons of the two search methods. |
We proposed an improved dichotomous search frequency offset estimator for burst-mode CPM. The estimator can operate independently of timing recovery and exhibits relatively low outlier. Most importantly, it offers reduced implementation complexity. Our proposed estimator eliminates the modulation removal and FFT operations, and it offers faster convergence rate compared to the dichotomous and modified dichotomous methods.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|









