The synthesis, ^[1] self-, ^[2] and directed-assembly^{[3– 5]} of nanoparticles (NPs) induced by an electromagnetic wave have been widely applied to create novel functional materials with special nanostructures. The dipole– dipole interaction (DDI) is crucial for the formation and stabilization of the assembly because it causes repulsion and attraction of the polarized NPs and affects the their configurations.^{[6, 7]} The diverse self-assembly morphologies of nanocubes are caused by the head-to-tail alignment of dipoles, i.e., the straight wires and sheets are organized by the nanocubes with 〈 100〉 and 〈 110〉 dipoles, ^{[8, 9]} respectively. Experiments and simulations demonstrate that the DDI induces the para-nematic and para-smectic phases of colloidal silica rods in external electric fields.^[10] The charged colloidal particles are organized into various colloidal structures, such as colloidal chains, vortex rings, three-dimensional (3D) aggregations, and two-dimensional (2D) crystal due to the electrohydrodynamic interaction and the induced dipolar interaction.^[11] More interestingly, the DDI leads to the formations of very rich phase diagrams of the colloidal particles in electrorheological and magnetorheological fluids, such as fluid, body-centered-orthorhombic, hexagonal-close-packed, body-centered-tetragonal, and face-centered-cubic phases, and determines the phase behaviors of these systems.^{[12, 13]} The CdTe NPs are self-assembled into chains under the electronic DDI between the NPs cores.^[14] Additionally, the geometry and optical properties of the aggregates which are irradiated by light are changed by the light-induced forces between the metallic NPs due to the induced DDI and dipole– field interaction.^[15] The reversible and irreversible NP suprastructures which are realized by light-induced self-assembly are mediated by the DDI and solvophobic effect.^{[16, 17]}

Similar effects have also been seen in magnetic NPs.^{[18, 19]} The single-phase-like magnetization alignment process exhibits in binary nanocrystal superlattices as a result of the collective dipolar interaction between two nanocrystals.^[20] The magnetic dipolar NPs which grow in gas phase are arranged in nanochains and nanorings.^[21]

The emphases of the research have been placed on the effects of various potentials^[5] on the static assembly. Indeed, the synthesis and assembly are a dynamic process from non-equilibrium to equilibrium state, and the components undergo a transition from transient to steady state. Although the dynamic behaviors of the NPs have been investigated in the aspect of the light-induced motion, ^[22] almost all attention has been focused on the stable motion of the NPs where the translation^[23] and rotation^{[24, 25]} are studied separately. Consequently, the instantaneous motions and the interaction between the translation and rotation have been ignored. The real dynamics of the individual NPs in the dynamic assembly have not been well understood.^[26] Therefore, it is of great importance for delicate modulation of the motion of the NPs in the dynamic synthesis and assembly.

Here, we present a system composed of two polarized nanorods in 3D free space and demonstrate their intrinsic dynamics under the electric DDI. We investigate the instantaneous relative motion between them by utilizing the general Euler– Lagrange equations. The results show that the relative translation and rotation of the two nanorods are nonlinear and closely dependent on their initial configuration. Moreover, the general conditions of the initial configuration that determine the two nanorods either repel or attract each other at initial time are derived. The relative motions in several simple 2D initial configurations show that the antiparallel and head-to-tail ordering stable self-assembly are respectively formed. Interestingly, for different initial 3D configurations, the dynamic relative attraction, repulsion, and oscillation with rotation are respectively demonstrated. Additionally, the theoretical schemes are presented to realize the relaxing, direct head-to-tail ordering, and direct antiparallel ordering stable self-assembly of the NPs with respect to different modes of the motion. Some of our results agree well with the results of experiments^{[9, 17]} and simulations.^{[7, 8]}

Nanoparticles polarized by the external electromagnetic field possess an electric dipole moment p = α (ω )E(r), where ω is the angular frequency of the incident monochromatic electromagnetic wave and E(r) represents its electric field intensity. The electric polarizability α (ω ) is decided by the Clausius– Mossotti formula for Rayleigh particles.^[27] However, the Rayleigh particle is regarded as a point-like dipole and only used to describe the translation of the NP without rotation. For determining the intrinsic rotation of the polarized nanorod involving the size of the dipole, we use p_i and l_i (i = 1, 2) to represent the effective dipole moment vector and size of the nanorod (dipole), individually. The interacting energy of the system in 3D vacuum is described by^[28]

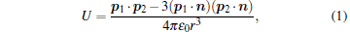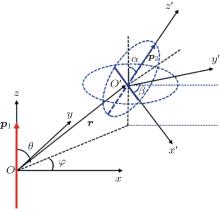
where ɛ ₀ is the dielectric constant in vacuum, r and n are the distance and normal unit vector between the centers of mass of the two nanorods as illustrated in Fig.  1.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. General configuration of the reference (fixed) nanorod (red solid line) and the free nanorod (blue dashed line). The O-xyz and O′ – x′ y′ z′ systems represent respectively the laboratory-fixed frame and the body-fixed frame. The distance r, polar angle θ , and azimuth angle φ describe the relative position of the two centers of mass. The nutation angle α and precession angle β (two Euler angles) determine their relative orientation in the laboratory-fixed frame. The p1 and p2 are the dipole moment vectors of the reference and free dipoles, respectively.

We assume that the dipole moment vector of the nanorod coincides with the axis of the nanorod. The center of mass of the reference (fixed) nanorod is located at the origin of the laboratory-fixed frame (O-xyz system) and the dipole moment vector is taken in the direction of the z axis p₁ = p₁z. The free nanorod is placed at an arbitrary point in space. The body-fixed frame (O′ -x′ y′ z′ system) is bound to the free nanorod and can be synchronously moved with it whose dipole moment vector is oriented along the z′ axis p₂ = p₂z′ . The z and z′ represent respectively the unit vectors of the z and z′ axes. The two frames are related by the Euler angles as shown in Fig.  1. In O-xyz system, by utilizing the coordinate transformation of Euler angles, equation  (1) can be rewritten as

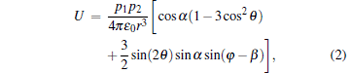where r, θ , and φ are the distance between the origin and the center of mass, polar angle, and azimuth angle of the center of mass of the free nanorod, individually. In addition, the nutation angle α and precession angle β describe the relative orientation between the two nanorods. The two nanorods are regarded as a thin rigid without spin angle.

The intrinsic dynamics of the system is equivalent to the relative motion between the two nanorods. The relative motion of the free nanorod with respect to the reference nanorod includes the translation of the center of mass and the rotation about its center of mass. Hence, the Lagrange function of the system can be expressed as

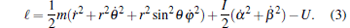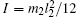
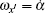
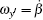
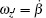
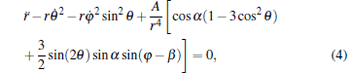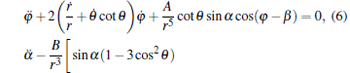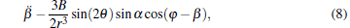Here, the first term on the right of Eq.  (3) describes the translational kinetic energy of the center of mass of the free nanorod in O-xyz system. The second term represents its rotational kinetic energy in O′ -x′ y′ z′ system. Its principle moments of inertia about x′ and y′ axes are identical because of its symmetry. According to the Euler angles formula, the components of the angular velocity with respect to the three body-fixed axes are , sin α , and cos α . The third term is the interaction energy determined by Eq.  (2). The equations of motion corresponding to the five degrees of freedom of the free nanorod are obtained by solving the Lagrange equation as follows:

where A = 3p₁p₂/(4π ɛ ₀m₂) and B = p₁p₂/(4π ɛ ₀I). Equations  (4)– (8) constitute a second-order nonlinear differential equation set and describe the evolutions of the five degrees of freedom r, θ , φ , α , and β with time in turn. Note that θ ≠ 0 and π in Eq.  (6) due to the fact that if θ = 0 or π , the center of mass of the free nanorod is located at the z axis and the azimuth angle φ is meaningless.

The radial force between the two nanorods determines them either to repel or attract each other for an arbitrary configuration and is given by

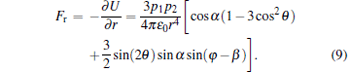If the four angles θ , φ , α , and β satisfy the relation F_r > 0, they repel each other. On the contrary, they attract each other when F_r < 0.

The relative rotation between the two nanorods is decided by the four components of the torque as follows:

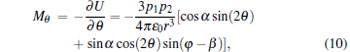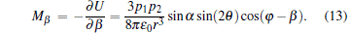Their repulsive and attractive processes are also affected by the torque except for the radial force because the transformation between the repulsive and attractive force F_r is impacted by the relative configuration which is determined by the torque. When the initial conditions are given, the influences mentioned above can be used to describe the succeeding motion.

As a simple application of the dynamics of the NPs, when the two nanorods are placed upon a substrate, their motion is regarded as 2D dynamic self-assembly. Here, we ignore the interaction between the nanorods and the substrate in order to describe their intrinsic motion. 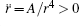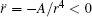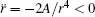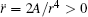On the one hand, if the two nanorods are parallel (θ = π /2 and α = 0) and antiparallel (θ = π /2 and α = π ) while the connecting line between the two centers of mass is perpendicular to the directions of the two dipole moment vectors, we find respectively and from Eq.  (4). It means that they repel and attract each other respectively. On the other hand, if they are collinear parallel (θ = 0 and α = 0) and antiparallel (θ = 0 and α = π ), we find respectively and . It indicates that they attract and repel each other respectively. The discussion above shows that the antiparallel with side-by-side and head-to-tail ordering stable self-assembly are formed respectively. Schmidle et al. investigated the self-assembly and phase diagram of 2D colloidal NPs with dipolar interaction based on the discontinuous molecular dynamics simulation. Their results demonstrate that the head-to-tail arrangement of the NPs is the most favorable and the side-by-side antiparallel configuration is more preferential than the counterpart with parallel configuration.^[7] Our results yield good agreement with the simulation results.

For the four cases above, the four initial angular accelerations equal to zero through substituting the initial conditions into Eqs.  (4)– (8). It illustrates that there is relative translation without rotation between the two nanorods because the interaction energy of the system in Eq.  (2) is only a function of r and independent of the other four angles.

The 3D dynamics of the polarized NP is more complex than its 2D situation. The relative motion of the two nanorods is nonlinear due to the co-instantaneous translation and rotation induced by the force and torque. Simply, we assume that the two nanorods are identical and have same dipole moment value p = 100 D, ^[6] size l = 100  nm, ^[24] and effective mass m = 1× 10^{− 17}  kg which is represented by the mass of gold sphere with the same diameter l.^[24] The initial distance between the two centers of mass is chosen as r₀ = 100l in order to satisfy the condition of dipole r₀ ≫ l. The initial linear and angular velocities of the free nanorod are set as zero. The distance r is intuitively expressed as a multiple of the size of the nanorod. We investigate the relative motion of the two nanorods by employing four-order Runge– Kutta method to solve numerically Eqs.  (4)– (8).

3.1. The relaxing self-assembly

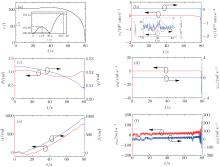
For the first configuration, the initial angles are θ = π /3, φ = π /6, α = π /4, and β = 3.5π /2. We have F_r > 0 by substituting the initial angles into Eq.  (9). The distance r does not monotonously increase, but oscillates in the motion as shown in Fig.  2(a). It can be clearly seen from the insert in Fig.  2(a) before 40  s. The free nanorod is repelled at the initial time, and r increases nonlinearly with time and reaches the local maximal value r = 101.46l at 11.8  s. At the same time, the linear velocity υ oscillates with a positive value while the linear acceleration a changes alternately its sign with oscillation as shown in the inset in Fig.  2(b)). The nutation angle α increases reversely with oscillation and the precession angle β oscillates around zero both up and down as illustrated in Fig.  2(e). The angular velocities ω _α and ω _β oscillate slightly around zero in Fig.  2(f). Next, r experiences a decreasing process and reaches the local minimal value r = 100.25l at t = 20.4  s (see the inset in Fig.  2(a)). The υ increases reversely after a decreasing process (see the inset in Fig.  2(b)). As the same process, α and β increase linearly with time, approximately, in Fig.  2(e). But the polar angle θ and azimuth angle φ change very little in the whole process (Fig.  2(c)). The polar angular velocity ω _θ and azimuth angular velocity ω _φ are nearly zero (Fig.  2(d)). The oscillation of a (or the force acting on the free nanorod) with alternate change of its sign (the inset in Fig.  2(b)) demonstrates that the free nanorod is alternately repelled and attracted with time due to the change of the configuration which is described by α and β (Fig.  2(e)). After 20.4  s, r increases to the local maximal value 104.12l at t = 36.5  s as shown in the inset in Fig.  2(a) and in turn decreases in the next attractive process (Fig.  2(a)). Both ω _α and ω _β maintain synchronous oscillation (Fig.  2(f)), and this leads to α and β increase linearly and synchronously with time (Fig.  2(e)), approximately. In the whole process, θ and φ hardly change and their angular velocities are equal to zero. At the terminal of the motion, the distance, angles, and angular velocities change rapidly (Fig.  2) because of the rapid increase of the force and the torque when the two nanorods are very close. In this case, the relaxing stable self-assembly of the polarized nanorods is formed, which experiences an oscillatory process before reaching the stable state.

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. The two nanorods attract each other with oscillation. The initial angles are θ = π /3, φ = π /6, α = π /4, and β = 3.5π /2. (a) The distance r as a function of time t. (b) The linear velocity υ and acceleration a as functions of time t. (c) The polar angle θ and azimuth angle φ as functions of time t. (d) The polar angular velocity ω θ and azimuth angular velocity ω φ as functions of time t. (e) The nutation angle α and precession angle β as functions of time t. (f) The nutation angular velocity ω α and precession angular velocity ω β as functions of time t. The inset in panel (a) shows the oscillating process of r and the red points represent the local maximum and minimum values of r. The inset in panel (b) shows the oscillating processes of υ and a before 40  s.

3.2. The direct head-to-tail self-assembly

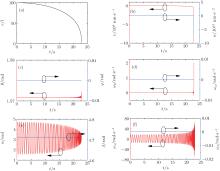
For the second configuration, the initial angles are θ = π /6, φ = π /3, α = π /4, and β = π /6. We have F_r < 0 at the initial time and the free nanorod is directly attracted. As illustrated in Fig.  3(a), r decreases nonlinearly with time. The θ decreases nonlinearly with time and φ varies barely (Fig.  3(c)). The α oscillates between 2  rad and ‒ 2  rad with decay while β increases to the local maximum value and in turn decreases to zero, and then increases reversely with oscillation (Fig.  3(e)). The ω _α and ω _β oscillate around zero both up and down (Fig.  3(f)). At the end of the motion, the linear velocity, linear acceleration, angles, and angular velocities change rapidly due to the strong short-distance DDI as shown in Figs.  3(b), 3(d), and 3(e). Finally, θ approaches to zero (Fig.  3(c)) and α oscillates with a small amplitude around zero (Fig.  3(e)). If the nanorod is placed in liquid, α decays faster and is finally stable at zero as the action of the additional damping torque. The results indicate that the head-to-tail arrangement of nanorods is realized when θ = α = 0. In this case, the direct head-to-tail ordering stable self-assembly of the polarized nanorods is formed. Zhang et al. simulated the dipole-induced self-assembly of PbSe nanocubes. They found that two dipoles tend to the direct head-to-tail arrangement in the assembled nanowires as the interaction energy between them is the minimum, and these results in the straight alignment of nanocubes^[8] the same as the previous transmission electron microscopy image experiment conducted by Cao et al.^[9] Our results agree with the results of experiments and simulations.

Fig.  3.

Figure Option ViewDownloadNew Window

Fig.  3. The two nanorods attract directly each other with head-to-tail. The initial angles are θ = π /6, φ = π /3, α = π /4, and β = π /6. (a) The distance r as a function of time t. (b) The linear velocity υ and acceleration a as functions of time t. (c) The polar angle θ and azimuth angle φ as functions of time t. (d) The polar angular velocity ω θ and azimuth angular velocity ω φ as functions of time t. (e) The nutation angle α and precession angle β as functions of time t. (f) The nutation angular velocity ω α and precession angular velocity ω β as functions of time t.

3.3. The direct antiparallel self-assembly

For the third configuration, the initial angles are θ = π /2, φ = 0, α = π /2, and β = 3π /4 (or β = 0). The two nanorods are perpendicular to each other out-plane (or in-plane) at the initial time. At the beginning of the motion, r, θ , and φ do not change as shown in Figs.  4(a) and 4(c) because of the force F_r = 0 from Eq.  (9). With the increase of time, their relative configuration has been changed due to the change of α . Afterward, the translation of the free nanorod emerges since the force does not maintain zero, and r in turn decreases with the change of α as shown in Fig.  4(a). The free nanorod experiences an attractive force directing the origin of the O-xyz frame and this is demonstrated by the negative υ and a (Fig.  4(b)). In the process of motion, α oscillates around the z axis (Fig.  1) with slow decay (Fig.  4(e)). The φ and β do not change (Figs.  4(c) and 4(e)) while θ changes very little (Fig.  4(c)). Finally, α decays to 3.14  rad which means that they are side-by-side with antiparallel because the interacting energy of the system is the lowest. In this case, the direct antiparallel ordering stable self-assembly of the polarized nanorods is formed. The prior experiment shows that low-power ultraviolet irradiation causes rapid trans-cis isomerization of the azobenzene dithiols (ADTs) and leads the molecules with induced electric dipole to aggregate and cross-link into supraspheres.^[17] The reason is that the cis-ADT-coated NPs with dipole moment are most favorable antiparallel arrangement (see Section 3 in the supporting material of Ref.  [16]) the same as our analytic results.

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. The two nanorods are antiparallel and attract each other. The initial angles are θ = π /2, φ = 0, α = π /2, and β = 3π /4. (a) The distance r as a function of time t. (b) The linear velocity υ and acceleration a as functions of time t. (c) The polar angle θ and azimuth angle φ as functions of time t. (d) The polar angular velocity ω θ and azimuth angular velocity ω φ as functions of time t. (e) The nutation angle α and precession angle β as functions of time t. (f) The nutation angular velocity ω α and precession angular velocity ω β as functions of time t.

The intrinsic dynamics of two interacting nanorods with electric dipole moments in 3D free space is presented. Based on the general Euler– Lagrange equations, the nonlinear evolutions of the five degrees of freedom which describe the relative translation and rotation between the two nanorods are derived. The results show that the relative motion of the two nanorods is nonlinear and closely dependent on their initial configuration. Moreover, the general conditions satisfied by the initial configuration are discussed in detail. The conditions determine the two nanorods to repel or attract each other at the initial time. In two simple 2D initial configurations, the antiparallel and head-to-tail ordering stable self-assembly are respectively formed. For three complex 3D initial configurations, the interesting relative attraction, repulsion, and oscillation with rotation of the two nanorods are respectively realized. The different modes of motion of the polarized NPs indicate that the relaxing, direct head-to-tail ordering and direct antiparallel ordering stable self-assembly can be formed. The time t = 14.8  s needed by the head-to-tail self-assembly is the shortest as shown in Fig.  3. The time t = 79.3  s needed by the relaxing self-assembly (Fig.  2) is longer than the time t = 22.9  s of the antiparallel self-assembly (Fig.  4). Some of our results agree well with results of the experiments and simulations.

Our work not only describes the dynamics of the individual NPs under electric DDI but also provides schemes to modulate precisely the modes and pathways of the motions of NPs and control the dynamic self-assembly process, ^{[29, 30]} at will, by setting the initial conditions or regulating the parameters of the external field. Our results have potential applications to assemble ordering nanostructures and avoid the formation of the defect. Our future work will consider the effects of the polarized state of NPs, gravity, external electromagnetic field, and viscosity of fluid on the motions of the NPs.