Cite this Article
Hadi M. A., Alam M. A., Roknuzzaman M., Nasir M. T., Islam A. K. M. A., Naqib S. H.. Structural, elastic, and electronic properties of recently discovered ternary silicide superconductor Li2IrSi3: An ab-initio study . Chinese Physics B, 24(11): 117401  
Permissions
Structural, elastic, and electronic properties of recently discovered ternary silicide superconductor Li2IrSi3: An ab-initio study
Hadi M. A.a), Alam M. A.b), Roknuzzaman M.c), Nasir M. T.a), Islam A. K. M. A.d), Naqib S. H.a)
Department of Physics, University of Rajshahi, Rajshahi-6205, Bangladesh
Department of Physics, Rajshahi University of Engineering and Technology, Rajshahi-6204, Bangladesh
Department of Physics, Jessore University of Science and Technology, Jessore-7408, Bangladesh
International Islamic University Chittagong, 154/A College road, Chittagong, Bangladesh

†Corresponding author. E-mail: salehnaqib@yahoo.com

Abstract

The structural, elastic, and electronic properties of the very recently discovered ternary silicide superconductor, Li2IrSi3, are calculated using an ab-initio technique. We adopt the plane-wave pseudopotential approach within the framework of the first-principles density functional theory (DFT) implemented by the CASTEP code. The calculated structural parameters show reasonable agreement with the experimental results. The elastic moduli of this interesting material are calculated for the first time. The electronic band structure and electronic energy density of states indicate the strong covalent Ir–Si and Si–Si bonding, which leads to the formation of the rigid structure of Li2IrSi3. Strong covalency gives rise to a high Debye temperature in this system. We discuss the theoretical results in detail in this paper.

Keyword: 74.10.+v; 61.50.Ah; 62.20.de; 71.15.Mb; silicide superconductor; crystal structure; elastic properties; electronic structures
1. Introduction

Transition metals often form covalent bonds with tetravalent silicon, because their electronegativities are comparable to that of silicon. The covalent character plays a vital role in realizing phonon-mediated superconductors with high Tc values. Transition metal silicides have already been identified as potential superconductors. For instance, V3Si exhibits superconductivity at Tc = 17  K.[1] In addition, the tunability of chemical potential by changing the transition metal may provide an additional channel in designing the ideal electronic structure[2] leading to higher Tc. For these reasons, the searching of new superconductors in doped covalent metals has received substantial attention. Very recently, using the conventional solid state reaction procedure, a new ternary transition metal silicide Li2IrSi3 was synthesized by Hirai et al.[2] This compound crystallizes in the hexagonal system with space group P63/mmc (No.  194) and shows weak-coupling phonon-mediated superconductivity below 3.7  K. The crystal structure of Li2IrSi3 is composed of Si triangles connected by Ir atoms, resulting in a three-dimensional network of covalent bonds. The antiprisms, IrSi6 stacking along the c axis are connected by Si triangles.

At the same time, Pyon et al.[3] prepared the polycrystalline samples of Li2IrSi3 by the arc-melting method and demonstrated that they were of a non-centrosymmetric trigonal structure with the space group P31c (No.  159). Resistivity and magnetization measurements revealed that Li2IrSi3 was a type-II superconductor with a Tc = 3.8  K. The crystal structure of Li2IrSi3 was found to consist of a planar kagome network of silicon atoms with Li and Ir spaced at unequal distances between the kagome layers, giving rise to a polar structure along the c axis. Though the two experimental groups[2, 3] reported two different space groups for the crystal structure of Li2IrSi3, most of their results are identical. The possible reason may be the similarity between crystal symmetries in both the trigonal and hexagonal systems. In fact, the hexagonal systems are in the special forms of a class of the trigonal system, since their faces are arranged regularly every sixty degrees around the triad axis. This is one of the reasons why some researchers prefer to group all the classes of these two systems together in sub-divisions of one large hexagonal system.[4] In this work, we consider only the hexagonal structure for the ab-initio calculations.

In this paper, we aim to explore the elastic and electronic properties of the newly discovered transition metal silicide superconductor Li2IrSi3 by means of first-principles calculations. Neither the elastic properties of Li2IrSi3 nor the mechanical properties of Li2IrSi3 have been studied yet. It is worth mentioning that the elastic properties are closely related to the crystal structure and the nature of bonding among the ions within the system. These factors, in turn, largely determine the phonon spectrum and the Debye temperature of the compound of interest. Therefore, elastic constants are the primary parameters for the understanding of mechanical properties: they have relevance to the phenomenon of superconductivity in superconducting compounds as well.

The rest of the present paper is as follows. In Section  2, a brief description of computational formalism used in this study is presented. All the results obtained in the present investigation are given in Section  3, while presented in Section  4 are the discussion and concluding remarks.

2. Computational procedures

The first-principles calculations reported herein were performed using the Cambridge serial total energy package (CASTEP) code, [5] which is based on the density functional theory (DFT)[6, 7] within the plane-wave pseudopotential approach. The Kohn– Sham equations were solved using the Perdew– Burke– Ernzorhof generalized gradient approximation (PBE-GGA)[8] for the exchange-correlation energy. Vanderbilt-type ultrasoft pseudopotentials[9] were used to model the electron– ion interactions. Throughout the calculations, a plane-wave cutoff energy of 500 eV was chosen to determine the number of plane waves in expansion. The crystal structures were fully relaxed by the Broyden– Fletcher– Goldfrab– Shanno (BFGS) minimization technique.[10] Special k-points sampling integration over the Brillouin zone was employed by using the Monkhorst– Pack scheme[11] with the 15× 15× 8 mesh. This set of parameters uses the tolerance in the self-consistent field calculation of 5× 10− 7  eV/atom, the change in total energy of 5× 10− 6  eV/atom, the maximum force of 0.01  eV/Å , the maximum stress of 0.02  GPa, and the maximum atomic displacement of 5× 10− 4  Å .

The CASTEP calculates the elastic properties from the first-principles using the finite strain theory, [12] which gives the elastic constants as the proportional coefficients relating the applied strain to the computed stress, σ i = Ci jε j. From Ci j, the polycrystalline bulk modulus B and shear modulus G were further evaluated using the Voigt– Reuss– Hill approximation.[13– 15] In addition, the Young’ s modulus Y, Poisson’ s ratio v, and shear anisotropy factor A were estimated using the equations Y = (9GB)/(3B + G), v = (3B − 2G)/(6B + 2G) and A = 4C44/(C11 + C33 − 2C13), respectively. The Debye temperature, Θ D, was determined from the following equations: Θ D = h/kB[(3n/4π )NAρ /M]1/3vm, with 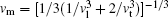, vl = [(3B+ 4G)/3ρ ]1/2, and vt = [G/ρ ]1/2. Here, vl and vt are the longitudinal and transverse sound velocities that determine the average sound velocity vm in a solid.[16]

In the present calculations, the spin– orbit coupling (SOC) has not been taken into consideration though the heavy transition metal Ir with 5d orbital is involved in this new compound. As far as the structural optimization, elastic properties and bonding characteristics are concerned, inclusion of SOC only has a minor effect. For example, the inclusion of the SOC in the calculations done for the transition metal based MAX phases, like M2AlC (M = Ti, V, and Cr) and Mo2AC (A = Al, Si, P, Ga, Ge, As, and In) has little or no influence on such properties.[17, 18]

3. Results and discussion
3.1. Structural properties

Li2IrSi3 crystallizes in the hexagonal structure with space group P63/mmc (194). The unit cell has 12 atoms containing two formula units (Fig.  1). The fully relaxed structure is obtained by optimizing the geometry with respect to lattice constants and internal atomic positions. The optimized Li atoms are situated in the 4f Wyckoff site with fractional coordinates (1/3, 2/3, 0.55889). The Si atoms are located at the 6h Wyckoff position with fractional coordinates (0.34291, 0.17145, 3/4). The Ir atoms are positioned at the 2a Wyckoff site with fractional coordinates (0, 0, 0). The calculated values of structural properties of Li2IrSi3 are presented in Table  1 along with the available experimental results. As can be seen from Table  1, the theoretical results are very close to the experimental values. This ensures the reliability of the present DFT-based first-principles calculations.

Fig.  1. Unit cell of hexagonal silicide superconductor Li2IrSi3.

Table 1. Lattice constants a and c, internal parameter z, hexagonal ratio c/a, unit cell volume V, and bulk modulus B with its pressure derivative B′ for hexagonal Li2IrSi3.
3.2. Elastic properties

Table  2 lists our results for elastic properties at zero pressure. Neither experimental data nor theoretical data on elastic properties for Li2IrSi3 are available. Any mechanically stable hexagonal phase must conform to the conditions known as the Born criteria:[19]C11 > 0, (C11 − C12) > 0, C44 > 0, and 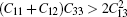. The calculated elastic constants completely satisfy the aforementioned conditions. Thus, we can affirm that Li2IrSi3 is mechanically stable.

The small values of C12 and C13 imply that Li2IrSi3 should be brittle in nature.[20] Pugh’ s criterion[21] and Frantsevich’ s rule[22] also support this classification. According to Pugh’ s criterion, a material should be brittle if its Pugh’ s ratio G/B > 0.5, otherwise it should be ductile. Frantsevich’ s rule has suggested the Poisson ratio v ∼ 0.33 as the critical value that separates the brittle and the ductile behavior. If the Poisson ratio v is less than 0.33, the mechanical property of the material is dominated by brittleness; if the Poisson ratio v is larger than 0.33, the mechanical property of the material mainly shows ductility. From Table  2, it is evident that the compound Li2IrSi3 is brittle in nature. The relatively low value of Poisson’ s ratio for Li2IrSi3 is indicative of its high degree of directional covalent bonding.

Table 2. Calculated single crystal elastic constants Ci j (GPa), polycrystalline bulk modulus B (GPa), shear modulus G (GPa), Young modulus Y (GPa), Pugh’ s ratio G/B, Poisson’ s ratio v, and shear anisotropy factor A of Li2IrSi3.

The difference between C11 and C33 suggests that Li2IrSi3 possesses anisotropy in the elastic property. Elastic anisotropy of a crystal reflects different characteristics of bonding in different directions. Essentially, almost all the known crystals are elastically anisotropic, and a proper description of such an anisotropic behavior has, therefore, an important implication in engineering science and crystal physics since it correlates with the possibility of the appearance of microcracks inside the crystal. The shear anisotropy factor for the {100} shear plane between the 〈 011〉 and 〈 010〉 directions is given by A = 4C44/(C11 + C33 − 2C13). For an isotropic crystal A = 1, any value smaller or greater than unity is a measure of the degree of elastic anisotropy possessed by the crystal. The calculated shear anisotropic factor shown in Table  2 deviates slightly from unity, which implies that the in-plane and out-of-plane inter-atomic interactions differ only slightly from each other. Another anisotropic factor is defined by the ratio between the linear compressibility coefficients along the c and a axes for the hexagonal crystal: kc/ka = (C11 + C12 − 2C13)/(C33 − C13). This has also been calculated. The calculated value of 0.66 reveals that the compressibility along the c axis is smaller than that along the a axis for this new superconductor Li2IrSi3. The comparatively low shear modulus indicates the low coefficient of friction and good machinability of Li2IrSi3.

The ratio of the bulk modulus B to C44 can be interpreted as a measure of plasticity.[23] A large value of B/C44 indicates that the corresponding material has excellent lubricating properties. The plasticity may also be estimated by the values of (C11 − C12) and Young’ s modulus Y.[24] The smaller values of (C11 − C12) and Y indicate a better plasticity of Li2IrSi3. The Debye temperature Θ D is calculated to be 488  K from the theoretical elastic moduli. The Θ D value is estimated to be 486  K by using the phonon contribution to the low temperature specific heat derived from experimental data of CP.[2] Very recently, the theoretical estimate of Θ D from lattice dynamical calculations yielded a value of 488  K, [25] exactly equal to the value estimated from the theoretical elastic moduli in this study. All these suggest that our calculations are reliable.

3.3. Electronic properties

The band structure of Li2IrSi3 with optimized lattice parameters along the high symmetry direction in the first Brillouin zone is shown in Fig.  2(a). The Fermi level of this superconductor lies just below the valence band maximum near the Γ point. The occupied valence bands spread widely from − 12.3  eV to the Fermi level EF. The valence band crosses the Fermi level, making the system conducting. The highly dispersive nature of the band structure along the Γ – A direction shows that the electronic transport along the c direction is not that different from that in the plane. Li2IrSi3 should be treated as a three-dimensional, nearly isotropic system.

Fig.  2. Electronic structures of Li2IrSi3. (a) Band structure at equilibrium lattice parameters along the high symmetry wave-vector, k and (b) total and partial energy densities of states. The Fermi level is set to be 0  eV.

The total and partial energy densities of states (DOSs) of Li2IrSi3 are shown in Fig.  2(b). The total DOS has a large value at the Fermi level N(EF), around 3.2 states per eV per unit cell, which is in reasonably good agreement with the value of 2.9 states per eV per unit cell found in Ref.  [2]. It should be mentioned that very recently Lu et al.[25] reported electronic band structure calculations with taking SOC into consideration and found N(EF) ∼ 3.5 states per eV per unit cell. This electronic energy DOS at the Fermi level is vitally important for superconductivity as the electron– phonon coupling varies linearly with N(EF). It has been found that inclusion of SOC has little effect on this parameter.[25] The primary effect of SOC is band splitting and a moderate shift in the energy in some of the dispersion curves. The Fermi surface topology remains almost identical with or without SOC. The main effect is the disappearance of the small hole pocket around the Γ -point with the inclusion of the SOC.[25]

The DOS at the Fermi level arises mainly from Ir 5d and Si 3p states. Once again, this finding confirms the metallic conductivity of Li2IrSi3. The wide valence band consists of several distinct peaks. It is observed that the lowest-lying valence bands with two peak structures in an energy range between − 12.3  eV and − 7.5  eV are formed almost entirely by 3s and 3p states of Si. The next peak structure in the total DOS located between − 7.5  eV and − 5.8  eV mainly originates from Si 3s, 3p and Ir 5d states. The second highest peak, between − 5.8  eV and − 3.3  eV, mainly consists of Si 3p and Ir 5d states. The highest peak in a range from − 3.3  eV to − 1.3  eV is derived from the strong hybridization of Si 3s, 3p with Ir 5d states. Li 2s has little contribution. The intense peak just below the Fermi level is composed of the dominant contributions from Si 3p and Ir 5d states. It is evident that within the energy range from − 12.3  eV to the Fermi level, a covalent interaction occurs between the constituting atoms due to the fact that states are degenerate with respect to both angular momentum and lattice site. It may be expected that the hybridization between 3s and 3p of Si in the lowest energy region should be responsible for the covalent Si– Si bond that forms a three-dimensional rigid network as a whole.[2] Further, a rather strong hybridization between Si 3p and Ir 5d states around the Fermi level would play a primary role in forming the covalent Ir– Si bond to crystallize the rigid structure of Li2IrSi3. In addition, some ionic characters can be expected due to the difference in electronegativity among the comprising elements. Therefore, the bonding nature in Li2IrSi3 may be described as a combination of metallic, covalent, and ionic. The gross features of our electronic structure study agree quite well with those found in Ref.  [25].

4. Conclusions

We have calculated the structural parameters, elastic properties, and electronic structures of newly discovered silicide superconductor Li2IrSi3 using the DFT-based first-principles method. The structural properties obtained are in good agreement with the experimental data.[2] The calculated elastic constants, obtained for the first time, allow us to conclude that the superconducting system Li2IrSi3 is mechanically stable. This new compound should have a low coefficient of friction and good machinability due to its low shear modulus. In addition, Li2IrSi3 can be characterized as brittle material and shows a small elastic anisotropy. The electronic structures of Li2IrSi3 show that its bonding is a combination of covalent, ionic, and metallic in nature. The rigid structure of Li2IrSi3 is the consequence of the strong covalent Ir– Si and Si– Si bonds. Besides affecting the elastic properties, this strong covalent bonding also has the potential to affect superconductivity itself. For covalent materials, the electron– phonon coupling constant can be expressed as λ = (M〈 ω 2〉 )− 1(dU/dz)2N(EF) (the Hopfield expression), where ω is a characteristic phonon frequency and dU/dz is the force due to electron– ion interaction. This equation, together with the weak coupling BCS equation for the superconducting transition temperature shows that Tc can be increased further by optimizing the values of ω and N(EF). The former has a direct link with the strength of the covalent bonds. Transition metal elements other than Ir might form stronger covalent bonds with Si 3p states and raise ω (∼ Θ D). The N(EF), on the other hand, can be tuned by doping holes in the system, which should result in a shift of the Fermi energy to a lower value, thereby increasing the EDOS at the Fermi level.

Reference
1 Hardy G F and Hulm J K 1953 Phys. Rev. 89 884 DOI:10.1103/PhysRev.89.884 [Cited within:1]
2 Hirai D, Kawakami R, Magdysyuk O, Dinnebier R E, Yaresko A and Takagi H 2014 J. Phys. Soc. Jpn. 83 103703 DOI:10.7566/JPSJ.83.103703 [Cited within:7]
3 Pyon S, Kudo K, Matsumura J, Ishii H, Matsuo G, Nohara M, Hojo H, Oka K, Azuma M, Garlea V O, Kodama K and Shamoto S 2014 J. Phys. Soc. Jpn. 83 093706 DOI:10.7566/JPSJ.83.093706 [Cited within:2]
4 Phillips F C 1971 An Introduction to Crystallography4th edn. New York John Wiley & Sons 89 90 [Cited within:1]
5 Clark S J, Segall M D, Pickard C J, Hasnip P J and Probert M I J Zeitschrift für Kristallographie 220 567 [Cited within:1]
6 Hohenberg P and Kohn W 1964 Phys. Rev. 136 864 DOI:10.1103/PhysRev.136.B864 [Cited within:1]
7 Kohn W and Sham L J 1965 Phys. Rev. 140 1133 DOI:10.1103/PhysRev.140.A1133 [Cited within:1]
8 Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 DOI:10.1103/PhysRevLett.77.3865 [Cited within:1]
9 Vand erbilt D 1990 Phys. Rev. B 41 7892 DOI:10.1103/PhysRevB.41.7892 [Cited within:1]
10 Fischer T H and Almlof J 1992 J. Phys. Chem. 96 9768 DOI:10.1021/j100203a036 [Cited within:1]
11 Monkhorst H J and Pack J D 1976 Phys. Rev. B 13 5188 DOI:10.1103/PhysRevB.13.5188 [Cited within:1]
12 Murnaghan F D 1951 Finite Deformation of an Elastic Solid New York Wiley & Sons [Cited within:1]
13 Voigt W 1928 Lehrbuch der Kristallphysik Leipzig Taubner Press [Cited within:1]
14 Reuss A and Angew Z 1929 Math. Mech. 9 49 DOI:10.1002/zamm.19290090104 [Cited within:1]
15 Hill R 1952 Proc. Phys. Soc. A 65 349 DOI:10.1088/0370-1298/65/5/307 [Cited within:1]
16 Anderson O L 1963 J. Phys. Chem. Solids 24 909 DOI:10.1016/0022-3697(63)90067-2 [Cited within:1]
17 Sun Z, Ahuja R, Li S and Schneider M 2003 Appl. Phys. Lett. 83 899 DOI:10.1063/1.1599038 [Cited within:1]
18 Khazaei M, Arai M, Sasaki T, Estili M and Sakka Y 2014 Sci. Technol. Adv. Mater. 15 014208 DOI:10.1088/1468-6996/15/1/014208 [Cited within:1]
19 Born M 1940 Math. Proc. Camb. Philos. Soc. 36 160 DOI:10.1017/S0305004100017138 [Cited within:1]
20 Romero M and Escamilla R 2012 Comp. Mater. Sci. 55 142 DOI:10.1016/j.commatsci.2011.11.038 [Cited within:1]
21 Pugh S F 1954 Philos. Mag. 45 823 DOI:10.1080/14786440808520496 [Cited within:1]
22 Frantsevich I N, Voronov F F and Bokuta S A 1983 Elastic Constants and Elastic Moduli of Metals and Insulators Hand book Naukova Dumka Kiev 60 180 [Cited within:1]
23 Vitos L, Korzhavyi P A and Johansson B 2003 Nat. Mater. 2 25 DOI:10.1038/nmat790 [Cited within:1]
24 Mattesini M, Ahuja R and Johansson B 2003 Phys. Rev. B 68 184108 DOI:10.1103/PhysRevB.68.184108 [Cited within:1]
25 Lu H Y, Yang N N, Geng L, Chen S, Yang Y, Lu W J, Wang W S and Sun J 2015 Europhys. Lett. 110 17003 DOI:10.1209/0295-5075/110/17003 [Cited within:5]