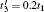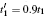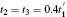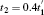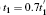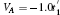The presence of the surface in materials can have a significant impact on their macroscopic behaviors.^{[2, 3]} The existence of surface states drives the surface property to be different from the bulk and plays a crucial role in transport.^{[4, 5]} The surface states propagating in cut crystals are extended along the parallel direction of the surface, but exponentially decay in the direction perpendicular to the surface. The most representative phenomena are the quantum Hall effect, ^{[6, 7]} the quantum spin Hall effect, ^{[8– 11]} topological insulator (TI), ^{[12, 13]} and topological superconductor (TSC).^[14] Besides the interest in topological states, a great deal of enthusiasm has been aroused for studying surface states in some conventional semiconductors (i.e., Si, Ge) and insulators (i.e., ABO₃ oxides) since their presence may influence their physical properties. The surface states can provide the room to accommodate surface mobile charges that may alter the conductive behavior. In some cases, such surface mobile charges can strongly couple with surface softened phonon modes, resulting in surface reconstruction such as the (111) surfaces of Si and Ge^{[15, 16]} and as a result, it may greatly affect physical properties of the devices. Thus, the study of surface states is not only important in the fundamental research such as the topological properties and the quantum entanglement, ^{[17, 18]} but also very useful for developing some future devices. Ab initio calculations are often recommended to investigate surface states and quantitatively figure out surface states emerging in cut crystals. Besides, the first-principles calculations, ^{[19, 20]} some analytical methods, such as Green’ s function method^{[21– 23]} and transfer matrix method (TMM), ^{[24, 25]} are also proposed to calculate surface states, particularly for weakly correlated materials where the band theory of solid state physics works.

As is well known, an infinite nD (n-dimensional) crystal consists of an infinite number of parallel (n − 1)D crystals which are periodically arrayed by coupling. For the sake of discussion, we take a 3D (three-dimensional) crystal as example. When n = 3, the (n − 1)D crystal represents a CP (crystal plane). Each CP is coupled with all its possible neighbor CPs. Except for some strongly correlated materials, in general, the hopping between CPs becomes weaker and weaker when the distance between them gets larger and larger. Thus, for most of the conventional crystals with low-index surfaces, the coupling between the 1NN (nearest neighbor) CPs will be dominant and the ones between the nNN (2 ≤ n < ∞ ) CPs are relatively weak. In the previous study, ^[1] we rigorously proved the absence of surface states at the level of the hopping approximation between the 1NN CPs when the original infinite crystal has GRS for each CP, resulting in the forward hopping matrix F to be equal to the backward one B, named as F– B dynamical symmetry. Furthermore, based on the perturbation theory, we also demonstrated that small perturbations from the couplings between the nNN (2 ≤ n < ∞ ) CPs and surface relaxations have no effect on the conclusion. The conclusion is applicable for any band crystals when each CP can contain any finite number of electron modes. However, for some possible naturally stable crystals with high-index surfaces and/or the strong SOC, the hopping between the 2NN CPs can be comparable with (even larger than) the one from the 1NN CPs and cannot be ignored. In fact, the SOC ∼ σ · L ∼ σ · (r × p) where σ and L are the spin and angular momenta of the electron. Just as the description in the Kane– Male model, ^[8] the coupling terms from the lattice site i to k for the intrinsic SOC must associate with at least two hopping steps via another neighbor lattice site j and be proportional to σ · (r_{i j} × r_jk). Thus, the dominant one should be from two 1NN bond (i → j and j → k) hoppings. Others relating with n (3 ≤ n < ∞ ) hopping steps are much smaller than the dominant one. The spin dependent hopping from the intrinsic SOC can be symmetric (F– B symmetry) (i.e., the 2NN one in zigzag edged graphene) or asymmetric (i.e., 1NN one in armchair edged graphene). For some topological insulators with strong SOC, the spin dependent hopping between the 1NN/2NN CPs can be comparable (even larger than) with the spin independent one from the 1NN CPs. Thus, in the present paper, we will focus on the effect of the hopping between the 2NN CPs on surface states. Meanwhile, the coupling between the nNN (3 ≤ n < ∞ ) CPs is also addressed as small perturbations for most of the crystals with low-index surfaces.

Here, we not only focus on such model crystals with Type I: “ · · · – P– P– P– P– · · · ” and II “ · · · – P– Q– P– Q– · · · ” where the original infinite crystal has the GRS, but we also consider the crystals with Type III: “ · · · – P= Q– P= Q– · · · ” where the original infinite crystal lacks the GRS. In three types, the letters P and Q represent CPs and the signs “ − ” and “ = ” indicate the distance of the 1NN CPs. It is worth mentioning that P and Q are distinct CPs in Type II and are identical or different in Type III. We will continue to discuss our previous result^[1] to see whether it is applicable or not in Type I when the finite symmetric couplings (F– B symmetry) between 2NN CPs are added. In this paper, we find that it is still applicable in Type I if each CP has one electron mode, but it may be invalid when each CP has n (2 ≤ n < ∞ ) electron modes. Moreover, we also demonstrate that surface states can emerge when the asymmetric hopping from the 2NN CPs is contained in Type I with one electron mode in each CP. For cut crystals with Type II, we have known that there are not any surface states for any band model crystals with the symmetric hopping from the 1NN CPs only when the original infinite crystal has the GRS for each CP.^[1] However, it will be shown that the coupling between the 2NN CPs is favorable to induce surface states no matter whether it is symmetric or not. While for cut crystals with Type III, surface states can be generated before the hopping from the 2NN CPs is considered and we also find that its existence is more helpful to promote the presence of surface states. These conclusions above are also valid for 1D/2D crystals where the “ surface” is just the “ edge” for 1D/2D crystals.

For an n-band semi-infinite crystal with Type I, each CP has a periodic structure and is a lower dimensional crystal than the original one. Since the wave vector k_‖ is still a good quantum number along the direction of the boundary plane, we can do the Fourier transformation in each CP. Now we adopt the diagonal representation of each CP Hamiltonian which can include the SOC, then the effective Hamiltonian can be written as at the level of the symmetric hopping approximation between the 1NN and 2NN CPs

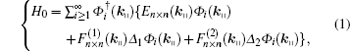where {Δ _lΦ _i(k_‖ ) = Φ _{i+ l}(k_‖ ) + Φ _{i− l}(k_‖ ) : l = 1, 2}, and {Φ _i(k_‖ ) = 0 : i ≤ 0}. represents the n × n hopping matrix from the CP P to its 1NN (2NN) one and E_{n× n}(k_‖ ) = diag(E₁(k_‖ ), E₂(k_‖ ), … , E_n(k_‖ )) where E_i(k_‖ ) = E ‒ ω _i(k_‖ ), E is the eigen energy of electron waves propagating in cut crystals and ω _i(k_‖ ) is the energy of renormalized eigen-modes at each CP. From now on, we will leave out k_‖ for simplicity.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Three type structures. (a) Type I: “ · · · – P– P– P– P– · · · ” . (b) Type II: “ · · · – P– Q– P– Q– · · · ” . (c) Type III: “ · · · – P= Q– P= Q– · · · ” .

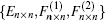
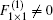
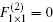
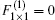
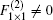
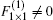
Firstly, we will focus on the one-band model, that is, n = 1 where are 1D matrices. For the cases of { and } and { and }, surface states are unallowable.^[1] Thus we concentrate our attention on the case of { and }. In fact, the one-band model with the hopping between the 1NN and 2NN CPs can be transformed into a two-band model with the hopping between the 1NN blocks when we take the 1NN CPs as one block: “ · · · -(P– P)– (P– P)– · · · ” (see Fig.  1(a)).

Each block has two coupled electron modes and the blocks are coupled to each other via the hopping between the 1NN blocks only. Then the effective quantum dynamical equation (QDE) reads

where {Ψ _n = 0 : n ⩽ 0}, , and

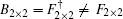
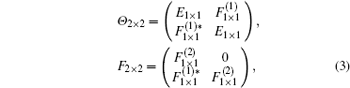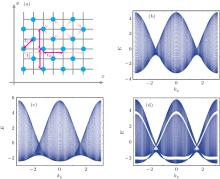
where we have B_{2× 2} ≠ F_{2× 2}, thus the one-band model with the hopping between the 1NN and 2NN CPs in its block representation is a two-band model without the F– B dynamical symmetry.^[1] Then, a question arises as to whether the surface states can exist or not. Here, we apply TMM to observe the behavior of surface states and can analytically prove that no surface states survive in such cut crystals with Type I when the symmetric hopping from the 2NN CPs is added in Appendix A. In order to check our conclusion, here we take the one-band model of a 2D crystal with the hopping between the 1NN and 2NN CPs for example (see Fig.  2(a)). By comparing the results obtained above with those attained in terms of the exact diagonalization method on a finite-size 2D crystal, we can see that these results are in good agreement with each other (see Figs.  2(b) and 2(c)) when the couplings from the 2NN CPs are symmetric 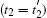. 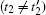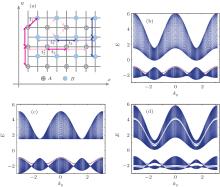Although a more general demonstration cannot be received for the special case with the longer range symmetric couplings (i.e., the one between the 3NN CPs), our numerical calculations have still shown the absence of edge states for some arbitrary parameters in the 2D crystal with the hopping from 1NN to 5NN CPs. In practice, although the intrinsic SOC interaction can involve the spin-dependent longer range hopping, which must associate with many hopping steps via lattice sites, it is usually much smaller than the one from the 2NN CPs and can roughly be treated as small perturbations for most of the crystals with low-index surfaces. Thus we focus on the spin-dependent intrinsic SOC from the 2NN CPs. Since it may be symmetric or asymmetric, depending on the cutting direction and the crystal structure symmetry, here we also focus on the effect of the asymmetric hopping from the 2NN CPs on surface states and find that surface states can be accommodated in such cut crystals with one electron mode in each CP when the hopping between the 2NN CPs is asymmetric by numerical discussion (see Fig.  2(d)).

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. (a) The schematic illustration of the lattice structure of a semi-infinite 2D crystal. (b)– (d) The dispersion relation of bulk states and edge states of a 2D crystal. Panels (b) and (c) show the absence of edge states when the symmetric hopping from the 2NN CPs is added. Panel (d) presents the existence of edge states when the hopping from the 2NN CPs is asymmetric. Here, (b) , (c) , and (d) t2 = 0.4t1 and .

The demonstrations above are limited in such cut crystals with the single electron mode in each CP. Now, we pay attention to the case where each CP has n (n ≥ 2) electron modes. Although we cannot give the rigorous and analytical demonstration for the presence or absence of surface states, some numerical calculations will present the existence of surface states in some simple models when the symmetric hopping from the 2NN CPs is included. It is well known that surface states can be accommodated in such cut crystals with the armchair edged graphene structure where each CP has two electron modes when the hopping from the 2NN is strong enough.^[1] Meanwhile, we also provide another example to understand our conclusion easily (see Fig.  3(a)). With the help of the exact diagonalization method, we can clearly see that edge states can emerge in such cut crystals (see Fig.  3(b)). From the discussion above, we can know that the coupling between the 2NN CPs is favorable to induce surface states in such cases even if the original crystal has the GRS for each CP in Type I. Moreover, as is discussed in Type I with one electron mode in each CP, we can note that surface states can be generated easily in such cut crystals with more than one electron mode in each CP when the hopping from the 2NN CPs is asymmetric.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. (a) The schematic illustration of the lattice structure of a semi-infinite 2D crystal. (b) The energy spectrum of bulk states and edge states obtained in terms of the exact diagonalization method. The parameters are , t2 = 0.75t1, t3 = t4 = 0.4t1, VA = 0.6t1, and VB = − 0.9t1.

For a cut crystal with Type II, when the symmetric hopping between the 2NN CPs is considered besides the one between the 1NN CPs, its QDEs is

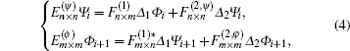where {Δ _lΦ _i = Φ _{i− l} + Φ _{i+ l}, Δ _lΨ _i = Ψ _{i− l} + Ψ _{i+ l} : l = 1, 2}, , , {Ψ _i = 0, Φ _{i+ 1} = 0 : i ≤ 0} and {i = 2j − 1 : j = 1, 2, … , ∞ }. and where and , and represent the n × n hopping matrices from one CP to its 2NN one.

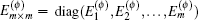
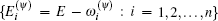
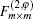
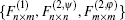
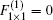
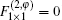
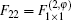
Firstly, we will draw attention to the simplest case, that is, n = m = 1 where become 1D matrices. We just focus on the Q cut crystal since the demonstration will be comparable for the P cut crystal. When or { and }, no surface states accommodate in such cut crystals.^[1] In fact, for other cases, the two-band model with the hopping between the 1NN and 2NN CPs can also be described by a two-band model with the hopping between the 1NN blocks only when the 1NN CPs are regarded as one block: “ · · · – (Q– P)– (Q– P)– · · · ” (see Fig.  1(b)). At this moment, the structure of its effective QDEs is identical to that in Eq.  (2) in its block representation where and . Since B_{2× 2} ≠ F_{2× 2} breaks the F– B dynamical symmetry, ^[1] it is natural to ask whether surface states can emerge or not. In the following, we can follow the similar steps discussed in Type I with one electron mode in each CP and analytically receive that surface states can be accommodated in such cut crystals. Remarkably, the boundary condition plays an important role for the presence of surface states in such cut crystals. To verify our analytical conclusion, here we take 2D and 3D crystals for example. For a 2D sample, its structure is shown in Fig.  4(a) and its energy spectrum for edge states is given with the help of the exact diagonalization method, which shows a good agreement with our demonstration (see Figs.  4(b) and 4(c)). While for a 3D crystal with the CsCl structure, we can still acquire the consistent results for two computational approaches, compatible with the previous study.^[21] Finally, we also find that surface states can emerge when the asymmetric hopping from the 2NN CPs is added by numerical analysis (see Fig.  4(d)).

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. (a) The schematic illustration of the lattice structure of a semi-infinite 2D crystal. (b)– (d) The energy spectrum of bulk states and edge states obtained in terms of the exact diagonalization method (blue line), while the dispersion relation of edge states given through TMM (red dash-line) in panels (b) and (c). Panels (b) and (c) show the presence of edge states when the symmetric hopping from the 2NN CPs is considered. (d) The presence of the asymmetric hopping from the 2NN CPs will be favorable to generate edge states. (b) . (c) and . (d) , t3 = 0.4t1, and . For all results we use VA = − 1.0t1 and VB = 1.5t1.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) The schematic illustration of the lattice structure of a semi-infinite 2D crystal. (b) The energy spectrum of bulk states and edge states obtained in terms of the exact diagonalization method. The parameters are , t2 = 0.75t1, , t3 = t4 = 0.4t1, t5 = 0.35t1, VA = 0.3t1, VB = 0.9t1, and VO = − 1.0t1.

Now, we simply address the model crystals with Type II where each CP has n (n ≥ 2) electron modes. Although we cannot analytically investigate the behavior of surface states, we can note that surface states can propagate in such cut crystals by some numerical calculations (see Fig.  5). From the demonstration above, we can find that the coupling between the 2NN CPs is much more helpful to generate surface states in Type II than Type I even if the original infinite crystal has the GRS for each CP in both types.

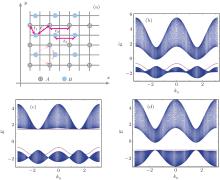
Finally, we simply discuss the cut crystal with the hoppings between the 1NN and 2NN CPs in Type III. For the case with one electron mode in each CP, it can also be transformed into a two-band model with the hopping between the 1NN blocks when we take the 1NN CPs as one block: “ · · · = (Q– P)= (Q– P)= · · · ” (see Fig.  1(c)). As is demonstrated in Type I with one electron mode in each CP, we can prove that surface states can emerge in such cut crystals after the finite symmetric couplings between 2NN CPs are added. To determine our conclusion, we study a 2D crystal with the structure shown in Fig.  6(a). Its dispersion relation for edge states is got by the exact diagonalization method, consistent with our conclusion (see Figs.  6(b)– 6(d)). Furthermore, for three type crystals, we can demonstrate that small surface relaxation and weak longer range hopping (the one between the nNN (3 ≤ n < ∞ ) CPs) cannot influence our result as discussed in the previous work.^[1]

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. (a) The schematic illustration of the lattice structure of a semi-infinite 2D crystal and (b)– (d) the dispersion relation of edge states obtained by means of the exact diagonalization method (blue line) and TMM (red dash-line). (b) and . (c) , and t3 = 0.0. (d) , t2 = 0.0 and . For all results we use and .

For most of the conventional crystals with low-index surfaces, the coupling between the 1NN CPs is dominant and the ones between the nNN (2 ≤ n < ∞ ) CPs are relatively weak and can be approximately treated as small perturbations. It has been proved^[1] that the weak hopping from the nNN (2 ≤ n < ∞ ) CPs has no effect on the behavior of surface states. However, for crystals with strong SOC, the dominant hopping terms from site i to k for the intrinsic SOC must associate with at least two hopping steps via site j and be proportional to σ · (r_{i j} × r_jk). Thus, the dominant intrinsic SOC interaction results from two 1NN bond (i → j and j → k) hoppings. In general, others relating with n (3 ≤ n < ∞ ) hopping steps are much smaller than the dominant one. Thus, we mainly focus on the hopping from the 2NN CPs on surface states. We have received the following conclusions by analytical and numerical calculations.

The study of surface states in cut crystals is fundamental in condensed-matter systems. Their presence/absence will influence their surface lattice structure as well as optical and transport properties. Meanwhile, some additional significant couplings between CPs will enhance the quantum entanglement of quantum states which also naturally induces the existence of surface states in cut crystals. There should be some internal relation between the topological quantum entanglement and surface states in cut crystals, but the relation still remains to be investigated.