Spintronics is a promising next-generation electronic technology based on manipulating the spin degrees of freedom. In comparison with the traditional electronic devices, those based on spintronics have advantages of low power consumption, fast response, and high storage density. Recently, prototype spintronics devices have been realized, such as a magnetic read head and memory-storage unit. One of the most important topics in spintronics is how to obtain high spin-polarized electron currents.^{[1, 2]} The magnetotunnel junction (MTJ) is a basic physical model for this type of spin-filtering effect. Numerous experimental^{[3– 6]} and theoretical^{[7– 9]} studies have focused on the spin-polarized tunneling properties of MTJs. In general, the spin-filter effect of MTJs is achieved by the spin-dependent electron transmission through the interface between the insulator (or semiconductor) and the ferromagnetic metals.^[10] The tunneling magnetoresistance (TMR) ratio is the most important parameter that determines the performance of MTJs.^[11] It is therefore crucial to achieve a high TMR ratio for practical applications of MTJs. One of the main challenges in obtaining a high TMR ratio is achieving a well-ordered interface in the MTJ.^{[11– 13]} Recently, both theoretical and experimental results^{[8, 14, 15]} have shown that by using graphene or h-BN sheets as the spacer in MTJs, high TMR ratios can be achieved.

Graphene, a single layer of carbon atoms in a honeycomb lattice, has attracted immense interest during the last decade because of its remarkable properties, such as high electron mobility, ^{[16, 17]} quantum Hall effect, ^{[18– 21]} high thermal conductivity, ^{[22, 23]} and long-distance scattering.^[24] As a next-generation, non-silicon, micro-electronic material, graphene also shows a great potential for spintronics applications.^{[25– 27]} Large-area and exceptionally high-quality epitaxial graphene layers can be grown on transition metal (TM) substrates.^{[28– 31]} Theoretical studies have shown that graphene retains a relatively well-integrated lattice structure and a perfect interface with TM substrates owing to its strong in-plane sp² hybridization.^{[32, 33]} Moreover, its electronic transport perpendicular to the plane shows strong selectivity near the high-symmetry K (K′ ) point in the reciprocal space, which makes graphene a good tunneling barrier and spin-selective insulator in MTJs. Recently, much effort has been devoted to MTJs constructed with graphene and 3d TMs Ni(111) and Co(111) because of the close match in the lattice constants of graphene and these metals. For example, Karpan et al.^{[8, 14]} reported that MTJs based on multilayer graphene and Ni or Co electrodes show perfect spin-filter effects. However, multilayer graphene has a very wide potential barrier, which increases scattering of transport electrons and greatly reduces the efficiency of the device. Therefore, finding suitable 3d TM electrodes that improve the spin-filter effect of the MTJs based on monolayer graphene is crucial for the application of graphene in spintronics devices.

In this study, we investigate the magnetism of a Cr/graphene/Cr MTJ by calculating the local density of states (LDOS) and k_∥ -resolved transmission conductance at zero bias. Importantly, the TMR ratio of the sandwich structure exceeds 100% and is close to that of a perfect spin filter. Moreover, a stable TMR ratio of Cr/graphene/Cr under an external bias is observed, demonstrating its potential in spintronics devices.

The most favorable configuration for graphene/Cr(111) is a graphene supercell matching the 1 × 1 Cr metal cell as shown in Figs. 1(a) and 1(b). The lattice mismatch of the graphene and Cr(111) surfaces in the planar junction is less than 3%. We constructed the MTJ from two semi-infinite Cr(111) electrodes and monolayer graphene as shown in Fig. 1(c). In Figs. 1(a) and 1(b), the blue, pink, yellow, and orange spheres represent the carbon atoms on hollow (C₄, C₅, C₆), top (C₁), hcp (C₂), and fcc (C₃) sites, respectively. It can be seen that the C₁ atom adsorbs on the top site of the left metal electrode, but on the hcp site of the right metal electrode. However, the C₂ atom adsorbs on the top site of the right metal electrode, but on the hcp site of the left metal electrode. The C₃ adsorbs on the fcc sites of both electrodes. The C₄, C₅, and C₆ atoms adsorb on the hollow sites of both electrodes. According to the sites of the carbon atoms, there are four non-equivalent types of carbon atoms in the spacer, namely, C₁, C₂, C₃, and (C₄, C₅, C₆), which breaks the inversion symmetry of the MTJ. The asymmetric feature of the MTJ will induce asymmetric transport properties. To obtain the stable structures of the MTJ, the atomic coordinates were optimized using the Vienna ab initio simulation package based on the density functional theory. The total energy converges to 10^{− 5} eV and the atoms of the system are fully relaxed until the residual force is less than 0.01 eV/Å . The Perdew– Burke– Ernzerhof parameterized spin-polarized generalized gradient approximation^{[34, 35]} was used to describe the exchange– correlation functional. The quantum transport calculations were carried out with the real-space nonequilibrium Green’ s function method implemented in the Atomistix Toolkit package. It has been demonstrated that this method can effectively describe the TMR effect of MTJs with planar contacts (e.g., Fe/MgO/Fe) and the electronic properties of the TM.^[36] In the electronic transport calculations, the Brillouin zone was sampled using a 20 × 20 × 100 k-point grid, and the charge density and potentials were determined on a real-space grid with a mesh cutoff energy of 300 Ry. The total energy convergence was set at 10^{− 5} Ry. All computational parameters used in the present study were optimized. The TMR ratio is defined as TMR = (G_P − G_AP)/G_AP × 100% = (G_{↑ ↑} + G_{↓ ↓} – 2G_{↑ ↓} )/2G_{↑ ↓} × 100%, where G_{↑ ↑} and G_{↓ ↓} are the majority and the minority spin-resolved transmission conductances, respectively, when the magnetic configuration of the two Cr electrodes is parallel (P); and G_{↑ ↓} is the spin-resolved transmission conductance when the magnetic configuration of the two Cr electrodes is anti-parallel (AP).

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Top view of the graphene/Cr(111) planar junction (the large spheres represent the Cr atoms and the small spheres represent the C atoms). (b) Side view of the Cr/graphene/Cr junction; the nearest C– Cr distance is 2.22 Å after optimization. (c) Two-probe system of Cr/graphene/Cr; the blue and black represent the Cr and C atoms, respectively.

The spin transmission spectra of the Cr/graphene/Cr MTJ under equilibrium conditions (zero bias) are presented in Fig. 2. For the P configuration, the spin states split around the Fermi level E_F, and the transmission coefficient of the spin-up channel is much larger than that of the spin-down channel. In contrast, for the AP configuration, both spin channels display similar transmission coefficients at E_F. The transmission coefficients of the AP configuration are similar to those of the lower transmission channel of the P configuration; this result is similar to that reported for Ni/graphene_n/Ni.^[14] Furthermore, we calculated the TMR ratio of the Cr/graphene/Cr MTJ to be approximately 108%, which far exceeds the values reported for Ni/graphene/Ni (17%) and Co/graphene/Co (60%) MTJs.^[37] Considering the different computational methods used, we recalculated the TMR ratio of Ni/graphene/Ni to be 42%, which is still significantly lower than that of Cr/graphene/Cr. Thus, the Cr electrode is more favorable for graphene-based MTJs.

Fig. 2.

	Figure Option ViewDownloadNew Window
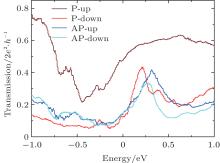	Fig. 2. Spin transmission spectra for the P and AP configurations of the Cr/graphene/Cr MTJ under zero bias. The Fermi level (EF) is set to zero.

To understand the transport properties of the Cr/graphene/Cr MTJ under zero bias, we calculated the LDOS in the real space of the system at E_F as shown in Fig. 3. The LDOS can clearly show the electron transport channels of a device in real space. For the P configuration, the LDOS of the spin-up channel is well distributed through the MTJ, whereas that of the spin-down channel is localized on the Cr electrodes, in particular, around the atoms close to graphene. The localization of the spin-down channel means that the effective transport channel mainly comes from the spin-up states. The blockage of the spin-down channel induced by the localization of the LDOS results in the transmission coefficient of the spin-up channel exceeding that of the spin-down channel. For the AP configuration, the LDOS is evenly distributed on graphene; the LDOS is only well distributed on one of the electrodes. Such quasi-localization in the AP configuration of both transport channels decreases the transmission coefficients. These results demonstrate that only the spin-up state of the P configuration can provide an effective transmission channel for the spin-polarized system.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. LDOS of the Cr/graphene/Cr MTJ in P and AP configurations under zero bias.

To explain the high TMR ratio of the system, we calculated the k_∥ -resolved transmission conductance and band structures, the results are shown in Fig. 4. The band structure shown in Fig. 4(b) indicates that the free-standing graphene is a semi-metal with its band structure linearly dispersed around E_F. The π and π * bands intersect at the K point in the Brillouin zone. The band structure of graphene with a supercell, as shown in Fig. 4(c), indicates that the K point is back-folded to the Γ (G) point. The band structures of the Cr/graphene/Cr MTJ are shown in Fig. 4(d). The interaction between the graphene sheet and Cr produces a bandgap for graphene of about 0.03 eV. In addition, the graphene is n-type doped by the electrodes. The results in Fig. 4(d) indicate that the electronic transport of the system occurs around the high-symmetry M and K points in reciprocal space because of the overlap of the band structures derived from graphene and the Cr electrodes at these k-points. For the MTJ, because there is spin-up transmission in the Cr(111) system around the G, M, and K points, as shown in Fig. 4(a), in the P configuration of the Cr/graphene/Cr MTJ, there is high k_∥ -resolved spin-up transmission conductance around the M and K points owing to the selection rules. Such selection rules can be directly evaluated from the k_∥ -resolved transmission conductance because this is the integral of the wave function at the Fermi surface projections.^[38] The k_∥ -resolved transmission conductance reflects the ability of the wave functions to penetrate from the left electrode to the right electrode at some specific k-points. In other words, the more compatible the wave functions on both sides of the interface, the larger the k_∥ -resolved transmission conductance. Although there is high spin-down transmission around the G and K points of the Cr electrodes along the (111) direction, the k_∥ -resolved transmission conductance for the spin-down state in the P configuration is low at the G, M, and K points because of the selection rules; that is, because of the incompatibility of the wave functions on both sides of the interface.^[38] The k_∥ -resolved transmission conductance for the AP configuration is mainly determined by the overlap between the spin-up and spin-down states of the two opposite sides of the junction. Consequently, the k_∥ -resolved transmission conductance of the AP configuration is lower at the G, M, and K points. It is these characteristics of the k_∥ -resolved transmission conductance that are directly responsible for the high TMR ratio. Moreover, an asymmetric k_∥ -resolved transmission conductance occurs for both spin channels in the AP configuration because of the asymmetric nature of the MTJ. The influence of the structural properties on the spin polarization can be determined from the Mulliken population of carbon atoms in the MTJ. For example, for the AP configuration under zero bias, the Mulliken population of carbon atoms shown in Table 1 indicates that there are four types of carbon atoms in the MTJ, which is in agreement with the four types of atom sites mentioned above. The asymmetric MTJ will produce different responses for the spin-up and spin-down states, which further contributes to the asymmetric Fermi surface projections for the two spin channels.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. (a) The k∥ -resolved transmission conductance through bulk Cr along the (111) direction and through the Cr/graphene/Cr MTJ. (b), (c) Band structures of graphene with a 1 × 1 unit cell and a supercell, respectively. (d) Band structure of the Cr/graphene/Cr MTJ; the red dots represent the contribution of the carbon states to the band derived from the projection of the wave function to the specific band according to different k points. The size of the red dots denotes the relative magnitude of the contribution of the carbon states to different k points. The projected density of state of graphene onto the total bands. The Fermi level is set to zero and the high-symmetry points are G = (0, 0, 0), K = (− 1/3, 2/3, 0), and M = (0, 1/2, 0).

Table 1.

Table 1.

Table 1. Mulliken population of C atoms in a Cr/graphene/Cr MTJ under biases of 0.5 V, 0.0 V, and − 0.5 V. The subscripted number is the sequence of C in the interfacial layer between graphene and the Cr electrode. Bias State C1 C2 C3 C4 C5 C6 Sum 0.5 V AP-up 2.03 1.98 2.02 2.08 2.08 2.08 12.27 AP-down 1.96 2.01 2.01 2.05 2.05 2.05 12.13 0.0 V AP-up 2.02 1.97 2.02 2.06 2.06 2.06 – AP-down 1.97 2.02 2.02 2.06 2.06 2.06 – − 0.5 V AP-up 1.98 1.94 1.98 2.04 2.14 2.03 12.11 AP-down 1.95 2.01 1.99 2.07 2.17 2.06 12.25

Table 1. Mulliken population of C atoms in a Cr/graphene/Cr MTJ under biases of 0.5 V, 0.0 V, and − 0.5 V. The subscripted number is the sequence of C in the interfacial layer between graphene and the Cr electrode.

The I– V curves were calculated to further evaluate the transport properties of the Cr/graphene/Cr MTJ under an external bias and the results are shown in Fig. 5(a). The spin-up I– V curve of the P configuration is linear with a notably larger current than that of the spin-down channel of the P configuration and of both channels of the AP configuration. The transmission conductance at the Fermi level under external bias is shown in Fig. 5(b). Our results show that the spin-up transmission of the P configuration is only slightly influenced by the external bias. From the LDOS of the two channels of the P and AP configurations shown in Fig. 3, we can see that only the spin-up channel of the P configuration is in an extended state. The other three channels are localized to different extents. The localized states are more sensitive to the external bias. Such sensitivity can be clearly shown by the dependence of the LDOS on the external bias, as shown in Fig. s1 in the supplementary materials. The transmission of the spin-down channel for the P configuration initially increases and then decreases with increasing bias. The turning points are 0.3 V and − 0.4 V for positive and negative biases, respectively. For the AP configuration, the spin-up transmission increases almost linearly with increasing bias. However, the transmission of the spin-down channel has a turning point at around 0.3 V under positive bias. The increase in transmission for the AP configuration under external bias will reduce the TMR ratio of the system. The turning point of the spin-down channel for the AP configuration only occurs under positive bias, which produces an asymmetric dependence of the TMR ratio on the external bias. Such an asymmetric dependence of the TMR ratio on the bias can be seen for the Cr/graphene/Cr MTJ in the inset of Fig. 5(b). The TMR ratio reduces in the bias window of [− 0.5 V, 0.2 V], which is similar to the behavior of the Fe/MgO/Fe MTJ reported by Yuasa.^[11] When the bias is larger than 0.2 V, the TMR ratio becomes constant, which is similar to the behavior reported previously for Ni/graphene₅/Ni^[9] and Fe-intercalated bilayer graphene sandwich structure.^[39] The bias-dependent asymmetrical characteristics of the TMR ratio result from the asymmetric transmission of the AP configuration, especially the spin-down channel. To further investigate this mechanism, we calculated the Mulliken population of carbon atoms for the AP configuration under 0.5 V and − 0.5 V external biases. The results are listed in Table 1 and show that the sum of the spin-up Mulliken population of carbon atoms is larger than that of the spin-down states (12.27 for spin-up and 12.13 for spin-down) under positive bias; however, under negative bias, this trend is reversed (12.11 for spin-up and 12.25 for spin-down). As mentioned above, the structure of the Cr/graphene/Cr MTJ is asymmetric. Moreover, the carbon atoms are in different planes and experience asymmetrical distortion, as shown in Fig. 1(b), meaning that they will have different coupling properties with the two metal electrodes. For the AP configuration, the electron gain and loss will be asymmetric because the spin polarization is different for the two Cr electrodes. This will serve to further induce the asymmetric electron potential between the two interfaces of the spacer. To clearly represent this effect, the spin-resolved total DOS of Cr on the top sites are shown in Fig. 6. The DOS of the spin-up states near the Fermi level is different from that of the spin-down states because of the asymmetric coupling between graphene and the two electrodes. For the AP configuration, if the left electrode is in the spin-up state corresponding to the spin-up channel of the DOS, the right electrode corresponds to the spin-down state of the DOS. The DOS will shift to higher (lower) energy under positive (negative) external bias. The different energy shifts of the DOS will result in different transport responses under positive and negative biases. Consequently, the transmission for the AP configuration has an asymmetric dependence on the external bias.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) The I– V curves for the P and AP configurations. (b) Bias-dependent transmission curves for the P and AP configurations. Inset: TMR ratio as a function of bias.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Spin-resolved total DOS of Cr on the nearest top-site carbon.

We have demonstrated that the TMR ratio of a Cr/graphene/Cr MTJ reaches 108% under zero bias, which is close to that of a perfect spin filter. Moreover, the TMR ratio is dependent on the external bias and decreases with increasing bias in the window of [− 0.5 V, 0.2 V]; however, when the bias is larger than 0.2 V, the TMR ratio is constant at 65%. This feature is markedly different from that of the conventional MgO-based MTJs in which the TMR continually decreases with increasing bias. The stable TMR ratio of the Cr/graphene/Cr MTJ under positive external bias demonstrates its potential for spintronics applications.