†Corresponding author. E-mail: zhang_ping@iapcm.ac.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 51071032).
Mechanical, electronic, and thermodynamic properties of zirconium carbide have been systematically studied using the ab initio calculations. The calculated equilibrium lattice parameter, bulk modulus, and elastic constants are all well consistent with the experimental data. The electronic band structure indicates that the mixture of C 2p and Zr 4d and 4p orbitals around the Fermi level makes a large covalent contribution to the chemical bonds between the C and Zr atoms. The Bader charge analysis suggests that there are about 1.71 electrons transferred from each Zr atom to its nearest C atom. Therefore, the Zr–C bond displays a mixed ionic/covalent character. The calculated phonon dispersions of ZrC are stable, coinciding with the experimental measurement. A drastic expansion in the volume of ZrC is seen with increasing temperature, while the bulk modulus decreases linearly. Based on the calculated phonon dispersion curves and within the quasi-harmonic approximation, the temperature dependence of the heat capacities is obtained, which gives a good description compared with the available experimental data.
Transition-metal carbides, such as TiC, ZrC, HfC, and TaC, are well known as hard refractory ceramic materials, sharing the same NaCl-type face centered cubic crystal structure.[1] As an important member of the large family, zirconium carbide (ZrC) possesses a high melting temperature (∼ 3670 K), decent refractory hardness (∼ 25 GPa), strong corrosion and oxidation resistance.[2– 4] Due to the presence of metallic bonding, the thermal and electrical conductivities of ZrC are similar to those of the zirconium metal.[5, 6] Beside, ZrC has a much lower density compared to other carbides like WC, TiC, and HfC. Thus, ZrC has an attractive potential in rocket/SCRAM jet engines and hypersonic spacecraft, where lower density and higher temperature load bearing capability are the most important requirements.[7] In addition, ZrC is one of the promising inert matrix materials in nuclear reactor applications according to the framework of the generation-IV international project, [8, 9] since it has a remarkably low neutron absorption cross-section and high resistance to the corrosion of nuclear fission products.[10, 11]
On account of these extraordinary properties of ZrC used in the extreme environment, several studies have already been conducted. The works concerned with the band structure and the density of states have been reported. However, still many features of bonding in this carbide have not been satisfactorily explained. For example, the electronic band structures from the augmented-plane-wave method given by Ihara et al.[12] demonstrated that the charge transfer from the Zr outermost s state to the C 2p state occurs, but did not give the exact value of electron transferred. The band structure of ZrC from a modified empirical-pseudopotential method obtained by Alward et al.[13] contradicts the result of Potoracha et al. from the tight-binding method, [14] especially in the energy of the lowest band derived from the C 2s state and the position near the Fermi level. On the other hand, relatively little is known regarding the phonon dispersions and the thermodynamic properties of ZrC from first-principles calculations. Last but not least, the temperature dependence of the bulk modulus and the volume dependence of energy are still lacking in the literature. All these facts bring about restraint to understand ZrC more deeply. Therefore, more intensive theoretical studies are necessary to confirm the mechanical, electronic, and thermal properties of ZrC, which encourage us to systematically investigate ZrC using the first-principles calculations based on the density functional theory (DFT).
According to this aim, the rest of this paper is organized as follows. The first-principles computational method is briefly introduced in Section 2. The calculated results are presented and discussed in Section 3. Finally, a summary of this study is given in Section 4. As will be shown, the calculated bulk properties of ZrC illustrate that the conventional generalized gradient approximation (GGA) for the exchange– correlation potential in DFT can give satisfactory results when compared to the experimental data. The bonding nature of ZrC exhibits a mixed ionic/covalent character, and there are about 1.71 electrons transferred from each Zr to C atom. The bulk modulus, lattice vibration energy, and specific heat at different temperatures are predicted by the quasi-harmonic approximation (QHA) based on the phonon density of states, providing a good comparison or reference with experiments.
The first-principles total-energy calculations are carried out using the projector-augmented-wave (PAW) pseudopotential[15] within DFT[16] as implemented in the Vienna ab initio simulations package (VASP).[17] The exchange and correlation effects are described by the GGA in the Perdew– Burke– Ernzerhof (PBE) form.[18] The valence configurations of 4s24p65s24d2 and 2s22p2 are explicitly included for Zr and C, respectively. The cutoff energy for the plane-wave basis set is 500 eV. The integration over the Brillouin zone (BZ) is carried out on 11 × 11 × 11 Monkhorst– Pack k-point meshes[19] for structural calculations, which proves to be sufficient for energy convergence of less than 1.0 × 10− 6 eV per atom. A dense 19 × 19 × 19 k-point mesh is selected to yield the electronic band structure, the density of states, and the charge density distribution.
In order to calculate the elastic constants of ZrC, we impose a small strain on the equilibrium cubic cell. The crystal total energy E(V, ϵ ) can be expanded as a Taylor series[20]
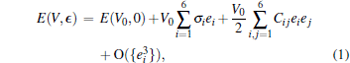
where E(V0, 0) is the energy of the undistorted lattice of volume V0, Cij are the elastic constants, and ϵ is the strain tensor which has matrix elements ε ij (i, j = 1, 2, 3)
 |
Therefore, the three lattice vectors defining the unstrained Bravais lattice {ak, k = 1, 2, 3} are transformed to the strained vectors {ak
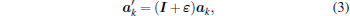 |
where I is a unit 3 × 3 matrix. Lattice vectors ak and ak
For the cubic structure, there are only three independent elastic constants C11, C12, and C44. Therefore we just need to employ three different strains to calculate them as follows: ϵ 1 = (δ , δ , 0, 0, 0, 0), ϵ 2 = (δ , − δ , 0, 0, 0, 0), ϵ 3 = (0, 0, 0, δ , δ , 0), where the Voigt notation has been used. The strain amplitude δ is varied in steps of 0.02 from − 0.06 to 0.06 and the total energies E(V, δ ) at these strain steps are calculated.
In order to obtain the equilibrium volume of ZrC, a series of total energies at different volumes around the experimental data are calculated. Then these energies are fitted as a function of volume to the third-order Birch– Murnaghan equation of state (BMEOS)[22] to obtain the theoretical equilibrium lattice parameter a0, bulk modulus B, and the pressure derivative of bulk modulus B′ , which are tabulated in Table 1. The experimental and other theoretical results are also presented in Table 1 for comparison. As shown in Table 1, our theoretical lattice parameter of 4.72 Å is in good agreement with the experimental value of 4.698 Å [22] and other theoretical results ranging from 4.68 Å to 4.72 Å .[23– 25] The obtained bulk modulus is 230.5 GPa, which is also consistent with the available experimental values and other theoretical results. The elastic constants, providing information about the resistance of materials to external stress or pressure, can be used to evaluate the stability of the crystals against elastic deformation. The calculated elastic constants of ZrC are gathered in Table 1, which are in good agreement with the experimental results.[26, 27] By comparing these three elastic constants, we find that C11 is much larger than the two others, indicating that ZrC is incompressible under uniaxial stress along the axis direction. Clearly, all these three elastic constants satisfy the mechanical stability criterion for the cubic structure, [20]C11 > 0, C44 > 0, C11 > | C12| , and (C11 + 2C12) > 0. From the predicted elastic constants, the corresponding bulk modulus and shear modulus can be calculated by employing the Voigt– Reuss– Hill (VRH) approach.[28] Note that the Voigt, Reuss, and Hill bulk moduli are identical for any cubic phase. As shown in Table 1, the obtained bulk modulus from the elastic constants is 4.5 GPa larger than the one from EOS fitting, which may be attributed to that the EOS fitting is not in the fully elastic region, unlike the determination of the elastic constants. The bulk modulus of 235.0 GPa for ZrC is smaller than the ones of 263 GPa for TiC[1] and 242 GPa for HfC.[29] The obtained Voigt, Reuss, and Hill shear moduli are close to each other (around 165 GPa), coinciding with the experimental values (162– 170 GPa).[27, 30, 31] The B/G ratio is 1.43, which is smaller than the critical value of 1.75, indicating the brittle nature of ZrC, since a value of 1.75 separates ductile and brittle materials according to the Pugh criterion.[32] The Young’ s modulus E and Poisson’ s ratio ν can be derived from the following relations:[33]
 |
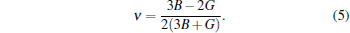 |
It can be clearly seen that the predicted Young’ s modulus of 400 GPa is quite large, indicating the strong ability to resist deformation. The obtained Poisson’ s ratio is 0.21, comparable to the derived values of 0.19[34] and 0.20[31] based on the experimentally determined elastic constants. Commonly, the microcracks in materials can be easily induced by significant elastic anisotropy, thus it is important to evaluate the anisotropic factor to understand the mechanical durability. For the cubic phase, the elastic anisotropy factor A is given by A = 2C44/(C11 − C12). The factor A is equal to 1.0 for isotropic crystals while a value different from 1.0 indicates elastic anisotropy. Due to the different atomic arrangements, the interaction forces between atoms in the (100), (110), and (111) crystal planes of ZrC are different, leading to the different performances of the stress– strain relationship. Therefore, our predicted anisotropy factor of 0.78 shows somewhat the anisotropic nature of ZrC.
| Table 1. Calculated lattice parameter a0 (Å ), elastic constants Cij (GPa), bulk modulus B (GPa), pressure derivative of the bulk modulus B′ , shear modulus G (GPa), Young’ s modulus E (GPa), and Poisson’ s ratio ν for ZrC. For comparison, other theoretical and experimental results are listed. |
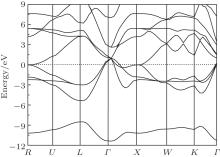
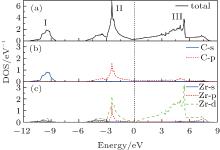
The most macroscopical properties of a material, such as hardness, elasticity, metallic property, and superconductivity, are closely connected to its electronic structure and chemical-bonding character. Thus, it is vital to investigate the electronic structure for ZrC. The electronic band structure of ZrC along selected high symmetry directions are depicted in Fig. 1, where the Fermi energy level is set to zero. From the band structure, we know that ZrC is a semimetal compound due to the occupied electronic orbitals over the Fermi level. Below the Fermi level, an energetically low-lying band, ranging from − 11.0 eV to − 8.0 eV, is evidently apart from the higher one. It originates from the C 2s state that contributes almost nothing to the bonding between the C and Zr atoms. As the energy scale increases, the C 2p orbital and Zr 4d and 4p orbitals form an obvious hybrid orbital below the Fermi level, extending to 1.0 eV above the Fermi energy, which contributes to the covalent bond between the C and Zr atoms. The energy bands above 1.0 eV are predominantly derived from the Zr 4d orbital. The band structure can be well understood with the help of electronic density of states (DOS), as depicted in Fig. 2. Clearly, the total DOS of ZrC is characterized by three obvious peaks, locating around − 9.5 eV, − 2.0 eV, and 5.0 eV, respectively. The peak I is mainly from the C 2s orbital. The mixture of C 2p and Zr 4d and 4p orbitals forms the large peak II, which makes a large contribution to the covalent bonds between the C and Zr atoms. The broad peak III mainly originated from the Zr 4d state.
The chemical bonding nature along the (110) plane of the valence charge density distribution for ZrC is shown in Fig. 3. Obviously, there is a nearly spherical distribution around Zr and C with slight deformation towards the directions to their nearest neighboring atoms. The charge density around the Zr and C ions is high while there is hardly a valence charge in the tetrahedron-hole interstitial region. This indicates the remarkable ionization of the Zr and C ions, which is consistent with the result derived by Ihara et al.[12] Furthermore, the electronic bridges between the Zr and C atoms can be clearly seen, which represent the covalent bonding nature of the Zr– C bonds. The bonding symmetry is evident. The line charge density at the bond point (CDb) along the nearest C– C, C– Zr, and Zr– Zr bonds is calculated respectively, and the results are collected in Table 2. As can be seen, the nearest C and Zr atoms are bonded by C– Zr bonds with mixed features of ionic and covalent. The CDb value of 0.0412 e/au3 for the C– Zr bonds is close to 0.044 e/au3 found for the B– Zr bond in ZrB2, but slightly larger than 0.033 e/au3 found for the B– Zr bond in ZrB12.[37] Besides, it is interesting to notice that there exist relatively weak covalent bonds between the C atoms with CDb = 0.0226 e/au3 and weak metal bonds between the Zr atoms with CDb = 0.0218 e/au3. To find out the electron transfer value, the Bader analysis[38, 39] is employed, which is an effective tool for studying the topology of the electron density and suitable for discussing the ionic/covalent character of a compound. The calculated results are presented in Table 2. The charge enclosed within the Bader volume can give a good approximation to the total electronic charge of an atom. Based on the Bader analysis, there are respectively 2.29 electrons and 5.71 electrons around the Zr and C atoms, indicating that approximately 1.71 electrons are transferred from each Zr to its nearest C atom. From the configuration of the extra-nuclear electrons, the Zr atom tends to lose 2 electrons to form Zr2+ . Compared to the Bader charge of 1.71, the effective valency in ZrC then can be represented as Zr+ 1.71C− 1.71. Therefore, the ionicity of the Zr– C bond is remarkable, with a mixture of weak covalency.
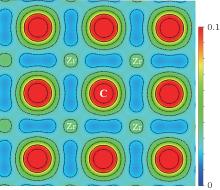 | Fig. 3. Contour plot of the charge density distribution in the (110) plane for ZrC. Contour lines are drawn from 0.0 to 0.1 at 0.01 e/au3 intervals. |
| Table 2. Calculated bond lengths (Å ) and charge densities (e/au3) at bond points (CBb) along the nearest C– C, C– Zr, and Zr– Zr bonds as well as effective atomic charges (e) and volumes (Å 3) according to Bader partitioning for ZrC. |
Considering that the thermodynamic properties of a material are related to its phonon dispersions, we employ the Hellmann– Feynman theorem[40] and the direct method[41] to obtain the phonon dispersions. The 5 × 5 × 5 Monkhorst– Pack k− point mesh is used for the 3 × 3 × 3 ZrC supercell (containing 54 atoms) to produce the phonon spectra. A pair of Zr and C atoms is displaced from their equilibrium positions with 0.03 Å amplitude to calculate the Hellmann– Feynman forces. The calculated phonon dispersion curves along the Γ – X– K– Γ – L directions in BZ and the corresponding phonon DOS are displayed in Fig. 4. The experimental data measured by Smith et al.[42] from the long-wavelength conduction electron screening are also presented in Fig. 4. The agreement between our calculation and the experimental data is excellent, strongly supporting the validity of the current theoretical model. For rock-salt type ZrC, there are only two atoms in its primitive cell. Therefore, six phonon modes exist in the dispersion relations. There is a distinct gap between the acoustic branches and the optic branches which results from the large mass difference between the Zr and C atoms. Thus the phonon DOS can be separated into two parts: one is caused by the vibrations of Zr atom in the range from 0 THz to 9.9 THz; the other one is mainly caused by the vibrations of light C atom with the range of 13.2– 20.8 THz. The stable phonon dispersions demonstrate that the thermodynamic properties of ZrC are stable, which further indicates that our following thermodynamic calculations are reliable.
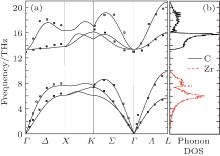 | Fig. 4. (a) Phonon dispersions and (b) phonon density of states of ZrC. The shown experimental data (square symbols) at room temperature are taken from Ref. [42]. |
Thermodynamical quantities such as the lattice vibration energy and the specific heat can be determined by phonon calculations using the quasiharmonic approximation (QHA).[43] Within this model, the Helmholtz free energy F as a function of temperature (T) and volume (V) can be written as
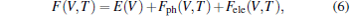
where E(V) stands for the ground-state total energy, Fph(V, T) is the phonon free energy at a given unit cell volume V, and Fele is the electronic excitation energy. Under QHA, Fph(V, T) can be calculated from phonon DOS g(ω ) by
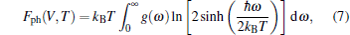 |
where ω = ω (V) represents the frequency of the phonon mode for volume V, g(ω ) is the phonon density of state, ħ is the Plank constant, and kB is the Boltzmann constant. Equation (7) contains some effects of unharmonics since the phonon frequency depends on the volume. In addition, the specific heat CV at constant volume can be expressed as
 |
Then the specific heat CP at constant pressure can be obtained by the following relationship:
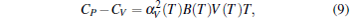 |
where the volume thermal expansion α V is defined as α V(T) = (1/V)(∂ V/∂ T)P.
The calculated volume dependence of the Helmholtz free energy F(V, T) curves with the locus of the equilibrium volume at different temperatures are plotted in Fig. 5. A drastic expansion in the equilibrium volume of ZrC can be clearly seen with increasing temperature from Fig. 5. By fitting these F– V data to BMEOS, the corresponding bulk modulus B(T) can be obtained as shown in Fig. 6. Obviously, the bulk modulus B(T) decreases linearly with increasing temperature. This kind of temperature effect in ZrC is the same as that in most compounds[44] and metals.[45] The specific heat capacities at constant volume CV and at constant pressure CP are given by Eqs. (8) and (9) and compared with the experimental data[46– 48] as well as theoretical results, [49, 50] as shown in Fig. 7. With increasing temperature, CV and CP both increase continuously. Our theoretical result for CP is found to be in good agreement with the experimental measurements[47] in the range of 300– 500 K. As the temperature further increases, the discrepancy between our result and the experimental data becomes legible with a maximum difference of 4 J· mol− 1· K− 1. It may be mainly attributed to the quasi-harmonic approximation used, where the anharmonic effects play a non-negligible role at high temperature.
 | Fig. 5. Volume dependence of the Helmholtz free energy F(T, V) and the locus of the minimum of the free energy at different temperatures for ZrC. |
Based on the DFT, we performed first-principles calculations to systematically study the mechanical, electronic, and thermodynamic properties of ZrC. The obtained ground-state equilibrium lattice parameter, bulk modulus with its derived modulus, and elastic constants, are all in good agreement with recent experimental data or previous theoretical results. The mixture of C 2p and Zr 4d and 4p orbitals around the Fermi level makes a large contribution to the covalent bonds between the Zr and C atoms in the ZrC matrix. The Bader analysis shows that the valency of ZrC can be expressed as Zr+ 1.71C− 1.71. Thus the Zr– C bond displays a mixed ionic/covalent character. The phonon dispersions of ZrC are stable, coinciding with the experimental measurements. We have further predicted the thermodynamic properties of ZrC. As the temperature increases, the volume expansion of ZrC is evident, while the bulk modulus decreases linearly. The specific heat at constant pressure agrees well with the experimental data in a relatively low temperature range (T < 500 K), while in the range of high temperatures, the anharmonic effects must be involved to predict more reliable results. We expect that these theoretical results of ZrC will be helpful for its practical application in the rocket engine and nuclear industry.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|