†Corresponding author. E-mail: qihong@hit.edu.cn
*Project supported by the Major National Scientific Instruments and Equipment Development Special Foundation of China (Grant No. 51327803), the National Natural Science Foundation of China (Grant No. 51476043), and the Fund of Tianjin Key Laboratory of Civil Aircraft Airworthiness and Maintenance in Civil Aviation University of China.
A hybrid least-square QR decomposition (LSQR)-particle swarm optimization (LSQR–PSO) algorithm was developed to estimate the three-dimensional (3D) temperature distributions and absorption coefficients simultaneously. The outgoing radiative intensities at the boundary surface of the absorbing media were simulated by the line-of-sight (LOS) method, which served as the input for the inverse analysis. The retrieval results showed that the 3D temperature distributions of the participating media with known radiative properties could be retrieved accurately using the LSQR algorithm, even with noisy data. For the participating media with unknown radiative properties, the 3D temperature distributions and absorption coefficients could be retrieved accurately using the LSQR–PSO algorithm even with measurement errors. It was also found that the temperature field could be estimated more accurately than the absorption coefficients. In order to gain insight into the effects on the accuracy of temperature distribution reconstruction, the selection of the detection direction and the angle between two detection directions was also analyzed.
Accurate prediction of temperature distribution plays an important role in many engineering fields, for instance combustion diagnostics, atmosphere radiation research, spectral emissivity measurement, combustion systems detection, optical tomography, particulate pollution emission and control, etc.[1– 11] Especially, the magnitude of the temperature distribution can have profound effects on the combustion performance and environmental impact, such as prediction of NOx emissions, which is very sensitive to the prediction of the flame temperature distribution. However, measurement of multi-dimensional flame temperature distribution is a particularly challenging task. It is very difficult to make high-accuracy predictions of temperature distribution in high-temperature combustion applications. To date, a fully independent, non-intrusive, in-situ technique for complete flame temperature fields is not available. The major reason for this deficiency is a lack of versatile, robust and computationally efficient reconstruction models to predict the temperature distribution of the participating media.
Theoretically speaking, the temperature measurement methods of the participating media can be divided into two categories: the contact measurement method and the non-contract (or non-intrusive) measurement method. The contact measurement mainly refers to measuring the temperature with different types of contact-type physical probes such as thermocouple, temperature-indicating paint, thermal resistance, etc. As the traditional temperature measurement methods, these contract methods have been broadly used in various scientific and industrial fields. However, all these contact methods have the disadvantages of disturbing the flow field, large measurement errors, and they cannot be used in many high-accuracy needed measurement situations. Especially, the contact probe technique can only be used for point measurements and cannot realize temperature field measurement. In addition, the experimental characterization of a flame temperature field making use of point measurement techniques is a time-consuming process, which constitutes a serious limitation for flame diagnostics and control in industrial combustion systems.[12] Compared with the contact measurement method, the non-contact type optical measurement technology based on the radiation image processing has the advantages of high precision measurement, non-invasive, minimal disturbance of the medium being probed and in-situ measurement, etc. Furthermore, the information of the three-dimensional temperature distribution can be obtained by this method. The problems of how to predict the temperature distributions from the radiative energy images can be merged into a kind of inverse radiative heat transfer problem. It has begun to draw attention in combustion fields recently and represents a very promising research direction and potential practical technology.
For the widely-used noncontact-type radiation imaging temperature measurement technology, the core problem is to develop an efficient, accurate, and steady algorithm to retrieve the temperature distribution and radiative properties of the participating media. During the last two decades, a considerable amount of work has been reported for determining the temperature profile or source term and radiative properties in participating media from various types of radiation measurements.[13– 23] A comprehensive review of inverse radiative transfer problems in participating medium was given by McCormick.[24] Liu et al.[1] developed a hybrid network search-conjugate gradient algorithm for simultaneous estimation of temperature distribution and the boundary emissivities for an emitting nonscattering, gray, plane-parallel medium from the knowledge of the exit radiation intensities at boundary surfaces. Liu also investigated the simultaneous identification of temperature profile and absorption coefficient in one-dimensional semitransparent media.[25] Qi et al.[2, 13] introduced the PSO algorithm into the inverse problem of radiation source and radiative properties firstly, and found that the PSO algorithm is efficient and robust for inverse radiation problems with the advantages of being independent for the initial value and there being no need to solve the objective function derivative, etc. Zhou et al.[14] introduced the Newton-type iteration algorithm and the least-squares method for simultaneous estimation of temperature distribution and the radiative properties for a one-dimensional (1D) media. Lou et al.[26] developed a decoupled method for simultaneous estimation of temperature distribution and the radiative properties for 1D optical thin axisymmetric flame or non-scattering participating media. Cui et al.[27] used the modified zone method to solve the direct problem and used the least square method to study the inversion problem of temperature distribution for 1D non-gray media. More specifically devoted to the cylindrical geometry, the study of Liu and Jiang[28] allows the reconstruction of absorption and temperature profiles inside gaseous axisymmetric flames. However, their method can only be used in 1D axisymmetric flames. Despite the relatively large interest expressed in inverse radiation problems of temperature or source term distributions in the participating medium, most of the work has considered 1D problems, and all of the work has been focused on regular or axisymmetric geometric systems. Recently, reconstruction of the temperature distribution in the multi-dimensional participating media has obtained increasingly more attention and a lot of work has been reported on the reconstruction of flame temperature fields by non-invasive infrared spectral measurements. The increasing availability of low-cost high spatial-resolution CCD cameras and data processing systems constitutes an additional incentive for the application of this technique to flames with practical relevance.[12] Due to the difficulties associated with the temperature distribution predictions, it has been common practice in participating medium (such as flame) temperature retrieval simulations to assume the radiative properties of the medium which are known according to the experience formulation or some experimental data. For instance, Lou et al.[29] used flame images to retrieve the flame emissivity and the uniform radiative properties of the flame in pulverized-coal-fired boiler furnaces by a modified Tikhonov regularization method. Klose et al.[4] researched the steady transmission optical imaging reconstruction problem based on the finite difference discrete coordinate method and Quasi-Newton method. Liu et al.[30] developed inverse radiation analysis for simultaneous estimation of temperature field and uniform radiative properties in participating medium using the LSQR method combined with the backward Monte Carlo method, and also used CCD cameras to simultaneously estimate the three-dimensional soot temperature and volume fraction fields in optically thin flames.[31, 32] Wang et al.[33] used flame images to retrieve the two-dimensional (2D) temperature field and particle concentration distribution of non-scattering pulverized-coal-fired flame with optimization algorithm. Snelling et al.[34] developed a multi-wavelength flame emission technique based on the line-of-sight (LOS) method for simultaneous estimation of soot temperature and soot volume fraction in axisymmetric laminar diffusion flames. To date, most of the research of retrieving temperature field in participating media need to know (or assume) the radiative properties of the media beforehand. To the best of the authors’ knowledge, there are few reports concerning simultaneous estimation of multi-dimensional temperature distribution and radiative properties.
The problem of retrieving the temperature field in participating media is a typical ill-posed problem. Traditional methods to solve this problem included the Tikhonov regularization method, [35] the truncated singular value decomposition (TSVD) method, [36] and the least squares QR decomposition (LSQR) method, [37] etc. All these regularization methods were proved to retrieve the temperature field successfully from the knowledge of the outgoing radiative intensities at boundary surfaces of absorbing media with known radiative properties. However, if the radiative properties are unknown beforehand, these methods were deficient and even cannot obtain reasonable estimation results. For the prediction of temperature distribution, the radiative properties have been largely assumed to be known due to the difficulty in retrieving the temperature and radiative properties simultaneously, even though it has been widely recognized that the radiative properties vary depending on the temperature values. Consequently, the uncertainty of assuming the radiative properties constitutes a major limitation to the accuracy of the non-invasive temperature retrieving techniques. In particular, the composition of the flame is not very clear, so the spectral radiative properties of the flame are not known a priori in many practical situations. In this condition, we need to seek new methods for reconstructing the temperature profiles of the flame.[28]
The objective of the present study is to develop a new hybrid least-square QR decomposition-particle swarm optimization (LSQR– PSO) algorithm to retrieve the 3D temperature distributions and the absorption coefficients simultaneously. The effects of detection direction and the angle between two detection directions on the reconstruction accuracy of the temperature field and radiative properties are also investigated. The remainder of the paper is organized as follows. The solving model for the direct problem is examined in Section 2. The theoretical models of the LSQR algorithm and the LSQR– PSO algorithm are described in Section 3. The problem of retrieving the 3D temperature field and radiative properties in participating media by the LSQR algorithm and LSQR– PSO algorithm are investigated in Section 4, respectively. The effects of the measurement errors on the accuracy of the inverse analysis are also examined. In Section 5, the main conclusions and perspectives are provided.
For the participating media, the radiation intensity in an arbitrary direction can be solved with the LOS method in the case of ignoring the scattering effect, and the radiative transfer equation (RTE) takes the form
 |
where I(r, τ ) represents the directional radiation intensity; τ denotes the optical thickness and τ = κ as; κ a is the absorption coefficient.
The directional radiation intensity at location τ can be obtained by integrating Eq. (1), and it can be written as
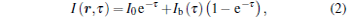 |
where I0 denotes the incident radiation intensity at the boundary surfaces.
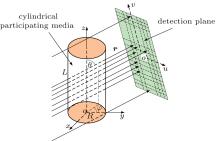
Considering the cylindrical participating media with the radius R and axial length L as shown in Fig. 1, all the boundary surfaces are supposed to be transparent (for example, the missile exhaust plume), and the environmental radiation is ignored. An ideal detection plane, which is assumed to be the radiation energy received by a certain element on the detection plane is only from the detection direction r(θ , φ ), is supposed to receive the exit radiative intensity, and the detection plane is perpendicular to the detection direction r(θ , φ ), where θ is the polar angle and φ is the azimuthal angle. Therefore, the exit radiative intensity in any direction r(θ , φ ) can be expressed as
 |
where τ j represents the optical thickness of the j-th grid cell along the detection line, n is the grid cell number along the detection line in direction r; Ibi denotes the Blackbody radiation intensity of the i-th grid cell along the detection line and 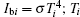
The detection plane in direction r is divided into M discrete elements, i.e., M beams of detection line along the direction r are given as shown in Fig. 1. Then the following equations can be obtained:
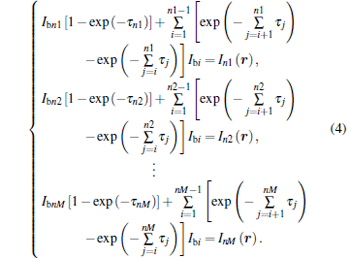 |
It can be written in the matrix form
 |
where A is the coefficient matrix; Ib denotes the blackbody radiation intensity vectors; In represents the exit radiative intensity vectors, namely the outgoing radiative intensities at the boundary surface of the media, and they are served as the input for the inverse analysis.
Therefore, for the calculation of the direct problem in the case of the given temperature distribution and absorption coefficient of media, the outgoing radiative intensities at the boundary surface can be calculated by solving Eq. (1) directly.
In the inverse problem, the radiative intensities received by the detectors are the measurement signals and the temperature field is the only unknown parameter for the participating media with known radiative properties, then the temperature field can be retrieved from the knowledge of the outgoing radiative intensities. For the temperature distribution reconstruction from the measured radiative intensities in the 3D participating media is a typical ill-posed inverse problem, the LSQR method is adopted to obtain the reasonable solutions.[37] The LSQR algorithm was firstly developed by Paige and Saunders[37] in 1982. Its basic idea is to turn the arbitrary coefficient matrix equations into equations whose coefficient matrix is a square matrix at first, and then solve the least square solution of the equations by the Lanczos method. It has particular advantages of quick convergence, high computing precision, good numerical stability, and suitable for solving the ill-posed problem. It is especially suitable for solving the linear equations with a large-scale sparse coefficient matrix, so the LSQR method is used to reconstruct the temperature field in the participating media in the present research.
In the case that the radiative properties are known, the linear equations of Eq. (5) can be solved by the LSQR algorithm directly to retrieve the 3D temperature distribution from the detected outgoing radiative intensities. However, when the radiative properties are unknown a priori in practice, the temperature field and radiative properties cannot be estimated simultaneously only by the LSQR algorithm. For the combined reconstruction of the temperature field and radiative properties, the objective function is commonly a multimodal function, and the solution of the entirely extremum problem is very difficult using the LSQR or traditional gradient-based methods. Thus based on the LSQR algorithm, a hybrid LSQR decomposition-particle swarm optimization (LSQR– PSO) method is developed and described next, with special focus on simultaneous reconstruction of the temperature distribution and radiative properties.
On many occasions, the radiative properties of a medium are unknown and often change with the operating condition, for example, the changement of the fuel-oxygen ratio in an industrial flame.[25] Under this condition, the temperature field and radiative properties should be reconstructed simultaneously from the radiative intensities received by detectors on the boundaries. If the radiative properties are unknown, equation (5) becomes a nonlinear equation and cannot be solved by the LSQR algorithm directly. Therefore, a hybrid LSQR– PSO algorithm is developed to retrieve the 3D temperature distributions and radiative properties simultaneously.
The PSO algorithm, which was first developed by Eberhart and Kennedy[38] in 1995, is an optimization algorithm based on the swarm intelligence with random search. The basic idea comes from the foraging behavior of birds. Group cooperation and competition among the particles produce swarm intelligence to guide the optimization search. As an efficient, simple parallel search algorithm, the PSO algorithm has been widely applied in all kinds of optimization problems in recent years.[39– 45] Each particle in the PSO algorithm denotes a solution candidate in the search space. It can adjust the flight path according to its own flight experience and its companions’ experience. Within the D-dimensional searching space, the particle swarm is composed of M individual particles, among which the i-th particle’ s velocity can be expressed as an n-dimensional vector Vi(vi1, vi2, … , vin). Similarly, the i-th particle’ s position could be described as n-dimensional vector Xi(xi1, xi2, … , xin). Each particle has a fitness value determined by the objective function value and a local best location Pi (the best fitness of the i-th particle encountered so far), which can be regarded as its flying experience. In addition, each particle swarm also has a global best position Pg (the global fitness of the i-th particle encountered so far) which can be deemed as the companion particles’ experience. In the basic PSO algorithm, the evolution equation of velocity and the position of the i-th particle in the (i + 1)-th generation are expressed as
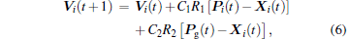 |
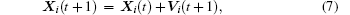 |
where i = 1, 2, … , M; C1 and C2 denote acceleration coefficients; R1 and R2 denote uniformly distributed random numbers in [0, 1]; Vi(t) represents the speed of the i-th particle at generation t; Vi(t + 1) represents the speed of the i-th particle at generation (t + 1); Xi(t) represents the current position of the i-th particle; Pi(t) is the local best position of the i-th particle at generation t; Pg(t) is the global best position at generation t.
Based on the PSO algorithm, a hybrid algorithm is developed by combining the stochastic searching capability of the PSO algorithm and the ill-posed inverse problem solving ability of the LSQR algorithm. The objective function is defined as
 |
where In2 is the measured radiative intensity in direction ψ 2, which is calculated by direct problem; 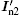
Step 1 The measured radiative intensities In1 and In2 in two different directions ψ 1 and ψ 2 which are calculated by the LOS method and are selected as input data for retrieving the temperature distributions and absorption coefficient simultaneously.
Step 2 Input system data and initialize the particle swarm, where the particle position represents the absorption coefficient of the media.
Step 3 Calculate the assumed temperature field T′ by the LSQR algorithm from the measured radiative intensity In1 of direction ψ 1 and the particle position (absorption coefficient).
Step 4 Calculate the assumed radiative intensity 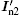
Step 5 For each particle, compare its fitness value to find the current individual best position Pi, and then choose the best Pi as the current global best position Pg.
Step 6 For each particle, calculate the new velocity using Eq. (6), and then update the particle position using Eq. (7).
Step 7 Check the stop criterion. If the fitness value is less than the setting tolerance or the iteration number exceeds the maximum number, go to Step 8; otherwise, loop to Step 3.
Step 8 Calculate the retrieval results of temperature field Test by the LSQR algorithm from the measured radiative intensity In1 of direction ψ 1 and the global best position (the retrieval value of absorption coefficient κ a, est).
Step 9 Print out the optimal solution to the radiative inverse problem.
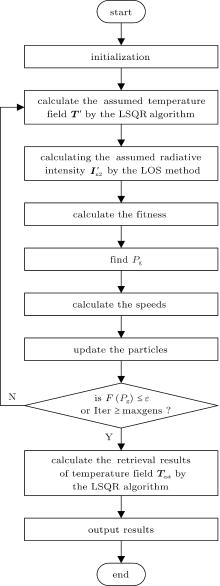
The detailed flowchart of retrieving the 3D temperature distributions and the absorption coefficient simultaneously by the hybrid LSQR– PSO algorithm is described in Fig. 2.
Considering the cylindrical participating media model as shown in Fig. 1, the radius is R = 0.5 m, and the axial length is L = 20 m. The cylindrical media is divided into 1000 grids, namely Nφ × Nr × Nz = 1 × 20 × 50. The number of detection line M is set as 10000, namely Nu × Nv = 100 × 100. The true temperature field of the media is assumed to be the function of z and r as
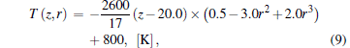 |
where z represents the axial coordinate of the cylinder, and r is the radial coordinate of the cylinder. The temperature distribution is shown in Fig. 3.
To demonstrate the effects of measurement errors on the predicted terms, the measured radiative intensity with random errors is obtained by adding normal distribution errors to the exact radiative intensity, as shown below
 |
where I represents the radiative intensity exiting the boundaries; ς is a normal distribution random variable with zero mean and standard unit deviation. The standard deviations of measured transmittance and reflectance σ for a γ measured error at 99% confidence are determined as
 |
For the sake of comparison, the relative error is defined as
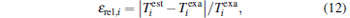 |
where 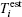
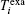
The maximum, mean, and minimum relative errors of retrieval results of the temperature field are defined as
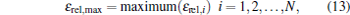 |
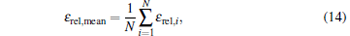 |
 |
where N is the grid number of the cylindrical media.
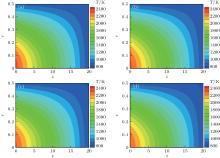
Taking the pure absorbing medium as an example, the radiative properties are known and the value of the absorption coefficient is assumed to be κ a = 0.5 m− 1. The true temperature distribution is given by Eq. (7). The 3D temperature distribution was retrieved from the measured radiative intensity at the detective direction of θ = 90° and φ = 45° using the LSQR algorithm. The measurement errors are assumed to be 0%, 1%, 3%, and 5%, respectively. The retrieval results are shown in Figs. 4(a)– 4(d).
 | Fig. 4. The reconstruction results of temperature field with known radiative properties: (a) γ = 0%. (b) γ = 1%. (c) γ = 3%. (d) γ = 5%. |
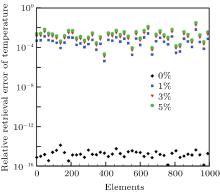
From Figs. 4(a)– 4(d), it can be seen that good estimated results of the temperature field can be obtained, even with measurement errors. The relative reconstruction error distributions of each grid cell with different measurement errors are shown in Fig. 5, and the maximum, minimum, and mean reconstruction errors of the retrieval temperature field with different measurement errors are shown in Fig. 6. As shown in Figs. 5 and 6, the retrieval accuracy of the temperature field is very high without measurement error and the relative errors range from 10− 16 to 10− 14. With the increase of measurement errors, the reconstruction error increases. However, even with 5% measurement error, the maximum reconstruction error is only 4.29% and the mean reconstruction error is only in the 10− 3 orders of magnitude. All the results show that the 3D temperature field can be retrieved very well by the LSQR algorithm in case where the radiative properties are known. The LSQR algorithm is proved to have high computational accuracy and stability, and is suitable to solve the inversion problem of a 3D temperature field of the participating media with known properties.
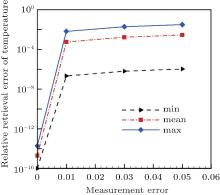 | Fig. 6. The maximum, minimum, and mean reconstruction error distributions of temperature field with known radiative properties. |
Moreover, the effects of the detective directions on the reconstruction accuracy of temperature field were also investigated in the present study in the case that the radiative properties were known. As the temperature distribution model is axisymmetric, only the effects of polar angle of the detective direction on the reconstruction accuracy of temperature field need to be studied. The azimuthal angle of the detection direction is assumed to be φ = 45° , and the polar angle θ is selected in the range of 10° – 170° with the interval of 10° to retrieve the temperature distribution using the LSQR algorithm with 0%, 1%, 3%, and 5% measurement errors, respectively. The mean reconstruction error distributions of temperature fields in different detection directions are shown in Fig. 7. From Fig. 7, it can be seen that the reconstruction accuracy of the temperature field firstly decreases and then increases with the polar angle of the detection direction increasing from 10° to 170° . In the case of no measurement errors, the mean reconstruction error of the temperature field is generally little, and the magnitude of maximum error is in the order of 10− 8. In particular, when the polar angle θ is equal to 90° , the mean reconstruction error of the temperature field is less than 10− 14. When a measuring error exists, the mean reconstruction error of the temperature field is the least in the case where the polar angle is in the range of 30° – 150° , and the retrieval accuracy varies a little with the change of the detective direction.
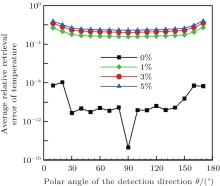 | Fig. 7. Effect of detection direction on the reconstruction accuracy of temperature field with known radiative properties. |
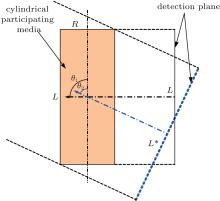
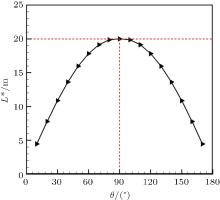
It is found that this phenomenon is caused by the projected area change of the media on the detective plane, with detection in different directions. The schematic diagram of the projected length change of the cylindrical media section in different directions is shown in Fig. 8. As shown in Fig. 9, the polar angle θ in the range of 10° – 170° with the interval of 10° is selected to calculate the corresponding projected length L* of the media’ s cross section. From Fig. 9, it can be seen that the projected length L* firstly increases and then decreases with the polar angle of the detection direction increasing from 10° to 170° . A too big or too small polar angle will cause the objective projected area (equal to 2RL* ) of the media on the detective plane to become too small. Consequently, less information about the detection can be obtained when the grid size of the detective plane is fixed, which will eventually lead to the decrease of retrieval accuracy. However, for the case of the detection polar angle in the range of 30° – 150° , the increase of the detection polar angle has a slight effect on the retrieval accuracy as shown in Fig. 7. In order to get the best retrieval accuracy, the polar angle of the detective direction is suggested to be close to 90° in the practical measurement.
In this case, the radiative properties are unknown a priori and the true value of the absorption coefficient is κ a = 0.5 m− 1. The search scope of κ a is set as [0.1– 1.0] m− 1. The true temperature distribution is the same as that shown in Fig. 3. The measurement error is selected as 0%, 1%, 3%, and 5% respectively. The 3D temperature distribution and absorption coefficient were reconstructed simultaneously using the hybrid LSQR– PSO algorithm. The radiative intensities received by the detectors at two detection directions of θ = 90° , φ = 45° , and θ = 30° , φ = 45° are chosen as input measurement data. The retrieval results of the absorption coefficient are listed in Table 1, and the retrieval results of the 3D temperature distribution are shown in Figs. 10(a)– 10(d). The relative reconstruction error distribution of the temperature field with different measurement errors are shown in Fig. 11. The maximum, minimum, and mean reconstruction errors of the temperature field and the reconstruction errors of absorption coefficient under different measurement errors are shown in Fig. 12.
 | Fig. 10. The reconstruction results of temperature field with unknown radiative properties: (a) γ = 0%, (b) γ = 1%, (c) γ = 3%, and (d) γ = 5%. |
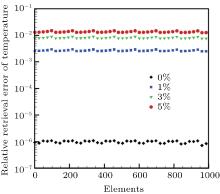 | Fig. 11. The reconstruction error distribution of temperature field with unknown radiative properties. |
From Table 1 and Fig. 12, it can be seen that the absorption coefficient can be retrieved accurately without measurement errors. When measurement error exists, the reconstruction error increases with the increase of the measurement error. All the results show that the absorption coefficient could be retrieved reasonably by the hybrid LSQR– PSO algorithm even with noisy data.
| Table 1. The reconstruction results of the absorption coefficient with true value κ a = 0.5 m− 1. |
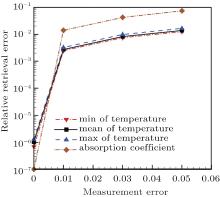 | Fig. 12. The maximum, minimum, and mean reconstruction error distributions of temperature field and absorption coefficient with unknown radiative properties. |
As shown in Fig. 10, it can be seen that good estimated results of the temperature field can be obtained, even with the random measurement errors. As shown in Figs. 11 and 12, the retrieval temperature field is very accurate in the case of no measurement errors and the relative error is in the range of 10− 6– 10− 7. The reconstruction error increases with the increase of measurement error, but even with 5% measurement error, the maximum reconstruction error is only 1.67% and the magnitude of mean reconstruction error is only in the order of 10− 2. Thus, it can be seen that the 3D temperature field can be retrieved accurately by the hybrid LSQR– PSO algorithm, even with measurement errors, which proves the hybrid LSQR– PSO algorithm is accurate and robust. In addition, compared with the absorption coefficient, the temperature field is easier to be retrieved with higher accuracy. The reason may be that the radiative intensity is not sensitive to the absorption coefficient which leads to the multi-value character of the retrieval absorption coefficient, which means that there exist multi retrieval results of absorption coefficient that can make the objective function equal to a very small value.
Furthermore, the effects of the angle between two detective directions on the reconstruction accuracy of temperature field and radiative properties were also investigated. As the retrieval result is more accurate with the polar angle θ = 90° according to the above analysis in Section 4.1, the polar angle of the first detection direction is set as θ 1 = 90° in the below discussion. The polar angle of the second detection direction is set as θ 2 = θ 1 − Δ θ , and Δ θ is the angle between two detective directions. The azimuthal angle of two detective directions is φ 1 = φ 2 = 45° . The effects of Δ θ on the reconstruction accuracy of the temperature field and radiative properties were analyzed while Δ θ changes in the range of 0° – 90° . The retrieval results and relative errors of the absorption coefficient in different detective directions are shown in Fig. 13. As shown in Fig. 13, if there is no measurement error, the effects of the angle between two detection directions on the reconstruction accuracy of the absorption coefficient are very small. A good retrieval result can be obtained independent of the angle between two detection directions, and the retrieval value of the absorption coefficient is very close to the true value. Even in the case of Δ θ is 1° , the retrieval relative error is only 0.01%. When the measurement error exists, the reconstruction accuracy of absorption coefficient firstly increases and then decreases and increases again with the decrease of the angle between two detection directions. The reason for this phenomenon is that the bigger the angle Δ θ is, the greater the difference of the information between two detection directions are, which benefit more for achieving accurate retrieval results. But with the increase of the angle between two detective directions, the polar angle θ 2 of the second detection direction becomes more and more deviated from 90° , then the information obtained in this direction decreases according to the above analysis in Section 4.1, and it is more unfavorable to achieve accurate retrieval results. Therefore, under the interaction of the above two kinds of behaviors produced the results are shown in Fig. 13.
 | Fig. 13. Effect of the polar angle between two detection directions on the reconstruction accuracy of absorption coefficient. |
Similarly, the mean reconstruction errors of temperature field in different detective directions are shown in Fig. 14. As shown in Fig. 14, when there is no measurement error, the mean reconstruction error of the temperature field is less than 10− 4. That is to say that very good retrieval results of temperature field can be obtained. When the measurement error exists, the reconstruction accuracy of the temperature field also firstly increases and then decreases and increases again with the decrease of the angle between two detection directions.
 | Fig. 14. Effect of the polar angle between two detection directions on the reconstruction accuracy of temperature field with unknown radiative properties. |
In the present research, the exit radiative intensities at boundary surfaces were simulated by the LOS method and served as an input for the inverse analysis. The LSQR decomposition algorithm was introduced to retrieve the 3D temperature distributions of absorbing media with known radiative properties. On this basis, a hybrid LSQR– PSO algorithm was developed to retrieve the 3D temperature distributions and absorption coefficient simultaneously. All the results show that the 3D temperature distributions of media could be retrieved very well by using the LSQR algorithm even with measurement errors in the case that the radiative properties are known. However, when the radiative properties of the media are unknown, the temperature distributions cannot be retrieved using the LSQR algorithm directly as the discretized equations were nonlinear. The 3D temperature distributions and absorption coefficient could be retrieved very well simultaneously by using the LSQR– PSO algorithm even with measurement errors, which proved the LSQR– PSO algorithm has good computational accuracy and stability. Meanwhile, it is found that the temperature field could be retrieved more accurately than the absorption coefficient even with measurement errors in the case of retrieving temperature field and radiative properties simultaneously. Furthermore, the effects of detection direction and the angle between two detection directions on the reconstruction accuracy of temperature field and radiative properties were investigated. The results show that, in the case that the radiative properties are known, the reconstruction accuracy of the temperature field firstly decreases and then increases with the increase of the polar angle of the detection direction, and the retrieve result is the best while the polar angle is near 90° and in the case that the radiative properties are unknown, the reconstruction accuracy of the temperature field and absorption coefficient firstly increases and then decreases and increases again with the decrease of the angle between two detective directions. Further study will focus on reconstructing the 3D temperature field, the absorption coefficient, and the scattering coefficient of participating media simultaneously by using the hybrid LSQR– PSO algorithm.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|