Ionization of atoms and molecules is a central problem in strong field physics.^[1] According to the Keldysh parameter, ^[2] ionization induced by strong laser fields is mainly divided into multiphoton ionization and tunneling ionization. In past decades, tunneling ionization has been extensively studied because it is tightly combined with a lot of fundamental strong field processes, such as rescattering, ^[3] high harmonic generation, ^{[4, 5]} attosecond pulse generation, ^[6] molecular imaging.^{[7, 8]} Tunneling ionization can be described by strong field approximation, ^[9] in which the Coulomb potential is neglected or treated as the first Born approximation. To fully preserve the Coulomb effect, one generally solves the time-dependent Schrö dinger equation (TDSE), ^{[10, 11]} which is precise and straightforward but time consuming. Alternatively, to include the Coulomb effect, classical trajectory Monte Carlo (CTMC) simulations^{[12– 15]} are carried on though quantum interferences are missing. Recently, Li et al. showed that by adding quantum phases on electron trajectories, the quantum interference can be preserved in CTMC simulations.^[16] Wang et al. combined the simulations of TDSE and CTMC to describe the photoionization.^[17]

For a molecule or atom exposed to a circularly polarized laser pulse, the electron departs from its parent ion along the instantaneous direction of the laser electric field when tunneling happens, but ultimately acquires a momentum perpendicular to that instantaneous laser electric field if the Coulomb potential can be neglected.^[18] Later on, Odenweller et al.^[19] found that the photoelectron momentum distribution is shifted away from the theoretical prediction by strong field approximation. In the tunneling ionization of noble gases in an elliptical polarized laser field, ^{[20– 22]} the electron momentum distribution also shifts away from the auxiliary axis of the elliptically polarized electric field. Recollision may still happen in circularly polarized laser fields.^[23] Both TDSE and CTMC simulations have been carried out and the importance of Coulomb effects on the electron momentum distribution has been recognized.

In this paper, we numerically solve the Newtonian equation for an ensemble of electrons in screened Coulomb potentials and circularly polarized laser fields. Different from the previous CTMC simulations, ^{[24, 25]} we directly start from the initial distribution which satisfies the Hamiltonian equation with a proper ground state energy. In our simulation, we screen the Coulomb potential at different radii, therefore we are able to watch the change of the electron trajectories in different Coulomb potentials step by step. The simulation results intuitively show how the Coulomb potential bends the electron trajectory, and therefore modifies the photoelectron momentum distribution. The rest of this paper is organized as follows. In Section 2, we introduce the numerical model. The simulation results are shown in Section 3. The paper ends with a conclusion in Section 4.

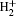
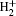
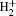
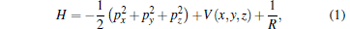Based on the CTMC idea, we describe the dynamics of the electron in the hydrogen molecular ion using a classical trajectory model in three spatial dimensions x– y– z. Two nuclei of lie along the y axis. The field-free Hamiltonian for is (atomic units are used throughout unless otherwise stated)

where the Coulomb potential is

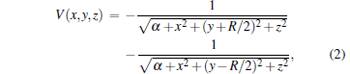where the internuclear distance is fixed at R = 2 a.u., and the soft-core parameter is α = 0.05. By setting the ground state energy at − 0.6 a.u., we obtain an ensemble of initial states for electrons in a six-dimensional phase space of p_x– p_y– p_z– x– y– z.^{[26, 27]} Electrons with initial positions and momenta are propagated under Newton’ s law, i.e., the motion of each particle is governed by

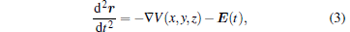where the laser field is written as

with ω and T being the frequency and period. The frequency of the laser pulse is ω = 0.057 a.u. and the laser intensity is variable. Obviously, the laser-induced dynamics mainly happens in the x– y plane. At the end of the propagation, we identify ionization for particles satisfying r > 100 a.u., where 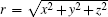. The simulation propagates long enough that photoelectron momenta are converged. We use the Runge– Kutta method to solve Eq. (3). One million particles are sampled in our simulations.

To see how the Coulomb potential acts on the photoelectron momentum distribution, we screen the Coulomb potential in the range r > r₀, and

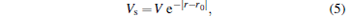where the screening radius r₀ is variable. The long-range part (r > r₀) is smoothly screened. Since almost all particles satisfying Eq. (1) distribute within the radius r = 6 initially, we gradually increase r₀ from 6 a.u. to 100 a.u. By tracing the electron trajectories departing from the same initial position and momentum but travelling in different screened potentials, we may clearly observe how the long-range part of the Coulomb potential bends the photoelectron trajectories. Thereby, the Coulomb effect on the final photoelectron momentum distribution can be intuitively explained.

We may point out that either a circularly or an elliptically polarized laser pulse can be used to steer the photoelectron, in which the Coulomb effect may be studied. However, the scenario induced by a circular polarized laser pulse would be easier to be understood because an elliptically polarized laser pulse will trigger larger or smaller ionization rates when the major electric field is parallel or perpendicular to the molecular axis and thus brings a more complex picture. To see the Coulomb-bending effect, we may also choose a hydrogen atom instead of as the target. Actually, the interaction of a circularly polarized laser pulse with is in principle very similar to the interaction of an elliptically polarized laser pulse with a hydrogen atom if the internuclear distance of is about 2 a.u. For in its equilibrium internuclear distance, the energy gap between 1sσ _g and 2pσ _u states is very large and charge resonance enhanced ionization will not happen.

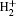
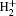
Figures 1(a)– 1(e) show the photoelectron momentum distribution when r₀ = 8, 10, 14, 20, and 100 a.u., respectively. We do not show photoelectron momentum distribution for a smaller r₀ because almost all electrons in this model initially distribute within a sphere with the radius r₀ = 6 a.u. Therefore, if the Coulomb potential is screened from a radius r₀ < 6 a.u., some electrons will fly away even though no laser field is introduced, thus the model cannot describe the physics any longer.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Photoelectron momentum distribution in the polarized plane when the screening radius r0 is (a) 8 a.u., (b) 10 a.u., (c) 14 a.u., (d) 20 a.u., (e) 100 a.u. (f) The drift angle as a function of r0. The laser intensity is 0.8 × 1014 W/cm2.

Though the circularly polarized laser pulse is isotropic, 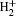is preferentially to be ionized when the instantaneous electric field is parallel to the molecular axis due to the strongest laser-electron coupling. The electron tunneling out along the molecular axis will be accelerated by the remaining electric field, and finally obtain the momentum − A(t₀) if the Coulomb potential can be neglected, where . Thus, the ultimate photoelectron momentum is perpendicular to the molecular axis in the case that the Coulomb potential is not considered. In reality, the Coulomb potential rotates the electron momentum distribution as thus the photoelectron momentum distribution shifts away from the y axis.

We define the drift angle as follows. We radially integrate the photoelectron momentum distribution and obtain the angle-resolved probability. The drift angle is the cross angle between the horizontal axis and the line passing through the original point and the maximum angle-resolved probability, as shown by the dashed curves in Fig. 1. In each panel, there are two separated patterns, corresponding to the preferred tunneling along y and − y axes. The electron momentum with the maximum probability density is slightly smaller than the laser vector potential, due to the haul of the Coulomb potential. With the increase of r₀, the photoelectron momentum distribution rotates clockwise in the laser polarization plane. The drift angle as a function of the screening distance is shown in Fig. 1(f), where the drift angle increases and finally converges. By the way, the ionization rate slightly decreases with the increase of r₀.

The CTMC calculations allow us to trace electron trajectories in the combination of the laser field and screened Coulomb potential. Figure 2 shows electron trajectories when the screening radius r₀ is 8 (blue solid line with dots), 10 (red dotted line), 14 (magenta dash-dotted line), 20 (green dashed line), and 100 (black solid line). Initially, the electron is at (x, y, z) = (− 2.2576, − 1.6299, 0.3942) and has the momentum (p_x, p_y, p_z) = (0.3365, − 0.2384, − 0.3516). It is obvious that the electron trajectories are different for the same electron travelling in different screened Coulomb potentials. The inset shows the zoom of trajectories close to nuclei, marked by the red ellipse. One may clearly see the trajectories are identical in the area r < 8. With the increase of r₀, the trajectories deviate from each other gradually, due to the bend of the Coulomb force.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Electron trajectories when the screening radius r0 is 8 (blue solid line with dots), 10 (red dotted line), 14 (magenta dash-dotted line), 20 (green dashed line), and 100 (black solid line). The inset is the zoom of the trajectories close to the nuclei. The laser parameters are the same as those in Fig. 1. The electron initial position is (x, y, z) = (− 2.2576, − 1.6299, 0.3942), and the initial momentum is (px, py, pz) = (0.3365, − 0.2384, − 0.3516).

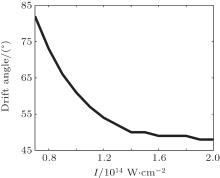
After diagnosing electron trajectories in screened Coulomb potentials, we study how the laser intensity changes the drift angle. Figure 3 shows the dependence of the drift angle on the laser intensity. Here, the unscreened Coulomb potential is used. When the laser intensity is very high, the strong electric field quickly strips off the electron from its parent ion, therefore, the Coulomb field acts on the electron only in a quite finite time interval. In this case, the electron momentum with the maximum probability will tend to point to the x axis and the drift angle is small, approaching to the case that the Coulomb potential can be neglected. On the contrary, when the laser intensity is relatively weak, the electron stays for a longer time with the nuclei, and the Coulomb effect on the electron’ s final momentum will be very important. Consequently, the drift angle is large.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The drift angle as a function of laser intensities.

The long-range part of the Coulomb potential not only drifts the photoelectron momentum distribution in the laser polarization plane, but also focuses the electron momentum in the perpendicular direction to the polarization plane. Figure 4(a) shows the scaled momentum distribution along the p_z axis for two screening radii r₀ = 8 a.u. and r₀ = 20 a.u., presented by black crosses and red dots, respectively. The solid and dashed Gaussian distribution curves fit the simulation results quite well. Figure 4(b) shows the full width at half maximum (FWHM) of p_z as a function of the screening radius. The black solid and red dashed curves present the results when the laser intensities are 2 × 10¹⁴ W/cm² and 1.5 × 10¹⁴ W/cm², respectively. With a larger r₀, the photoelectron has a narrower momentum distribution along the p_z axis, which is a direct proof of Coulomb focusing.^{[28– 30]} When the laser intensity is stronger, the electron leaves its parent ion quicker, hence, the Coulomb focusing is weaker and the p_z width is larger.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. (a) The scaled momentum distribution along the pz axis. The crosses and dots are simulation results when the Coulomb potential is screened at r0 = 8 a.u. and r0 = 20 a.u., respectively. The laser intensity is 0.8 × 1014 W/cm2. The simulation results are fitted with the black solid and red dashed Gaussian distribution curves. (b) The full width at half maximum of the momentum distribution in the pz axis as a function of the screening radius when the laser intensities are 2 × 1014 W/cm2 (black solid line) and 1.5 × 1014 W/cm2 (red dashed line).

In conclusion, by screening the Coulomb potential at different radii, we clearly see that electron trajectories are bent by Coulomb potentials. The distortion of electron trajectories results in the drift of the final photoelectron momentum distribution. In stronger laser fields, the electron escapes from the nuclei faster, and the drift angle of the momentum distribution is smaller. The Coulomb focusing of the electron momentum distribution in the plane perpendicular to the laser polarized plane is demonstrated. This study presents an intuitive picture of how the Coulomb potential affects the photoelectron momentum distribution of atoms in strong laser fields.