Derived from cavity quantum electrodynamics, a coupling system consisting of a semiconductor quantum dot (QD) and microcavity has been proved to have great potential in quantum information sciences.^{[1– 4]} In particular, double QDs have attracted much attention due to their unique characters.^{[5– 7]} Compared with in a single QD, the states in a double QD are strongly modified, leading to applications such as conditional quantum control, ^[8] spin-flip, ^[9] and entangled photon source.^[10] For uncoupled double QDs, the optical properties and energy eigenstates have been investigated by complicated luminescence spectrum and temporal dynamics.^{[11, 12]} For coupled double QDs (CDQDs), tunnel coupling or Coulomb coupling has been experimentally realized in recent years.^[13] Theoretically, CDQDs were treated by several methods.^{[14– 19]} Based on the four-level model, ^[14] phonon-mediated CDQDs– cavity coupling was taken into consideration and exciton occupation probability was analyzed in Ref.  [15], in which the effects of Coulomb interaction on the recombination of excitons were explored. By describing the Hamiltonian of the CDQDs as a complex Hamiltonian, ^[16] the influences of Coulomb interaction on light emission were discussed in CDQDs– metal sphere hybrid system.^[17] Adopting an equivalent Hamiltonian of two-level system, ^[18] the photons counting statistics of CDQDs– resonator system was investigated in Ref.  [19], determining a sub-Poissonian character under the resonant condition. Moreover, the CDQDs can be described by the dipole– dipole interaction, in which the photon emitted by an excited QD could be absorbed by the other QD. This interaction has been used to theoretically study two photon lasing properties and remote entanglement states in the QDs– cavity, ^[20] QDs– waveguide^[21] and atoms– cavity system.^[22] However, for CDQDs– cavity system, relevant work on the sub-Poissonian photon statistics, especially its dependence on laser frequency detuning, is lacking.

In the present work, we study the photon emission properties in the CDQDs– cavity system separately under continuous wave and pulse excitation, concluding the sub-Poissonian character of photon statistics at a certain excitation laser frequency. Besides, the generation of few-photon state is analyzed. We also propose a model to explain the sub-Poissonian phenomenon in the CDQDs system as being due to the interaction between off-resonant QD– cavity and single QD. Finally, a non-identical double QD case is studied to examine the robustness of our model.

A system consisting of microcavity and embedded CDQDs is considered. The QD is recognized as a two-level system. Under the rotating wave approximation (RWA), the system Hamiltonian H = H₀ + H_d is given by^[20]

where and σ _i are transition operators expressed as σ _i = | g_i〉 〈 e_i | , | g_i〉 and | e_i〉 are ground state and excited state of i-th QD, respectively, a and a^† are annihilation and creation operators of photons in the cavity mode respectively, ω _i and ω _c are frequencies of i-th QD and cavity mode respectively, g_i is coupling strength between i-th QD and cavity, E is the amplitude of the excitation laser, and V is the coupling strength between two QDs. H₀ contains free Hamiltonian and interaction Hamiltonian, while H_d is the driving Hamiltonian. Taking a rotating frame at the laser frequency ω _l, the Hamiltonian becomes

Here, Δ = ω _{1, 2, c} − ω _l is detuning between cavity frequency and excitation laser frequency, assuming that QDs and cavity are resonant for simplicity (if off-resonant analysis is considered, we will specifically point it out). Similar expressions of coupled QDs are also utilized in QD– nanoparticle– QD structure, ^[23] where coupling strength is given by dipole– dipole interaction.^[24] The incoherent process is modeled through standard Lindblad operators

In the above equation, κ is the decay rate of cavity, γ _i is the spontaneous emission rate of i-th QD. L(x) is the Lindblad operator defined as^[25]

To obtain the photon emission, we numerically solve the master equation with the aid of functions in the quantum optics toolbox, ^[26] calculating the second-order autocorrelation function under continuous wave excitation

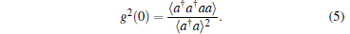Due to the low excitation we adopted here, the Fock state space used in our calculation is truncated at N = 5. The photon statistics can be represented by second-order autocorrelation function: sub-Poissonian (super-Poissonian) with g²(0) < 1 (> 1). We simulate the CDQDs– cavity system with the following parameters cited from Ref.  [27]: coupling strength g_i/2π = g/2π = 10  GHz, cavity decay rate κ /2π = 20  GHz, QD spontaneous emission rate γ _i/2π = γ /2π = 1  GHz, and coherent pumping rate E/2π = 1  GHz. It should be noticed that in the remaining part of the present paper, the 2π factor is omitted for simplification.

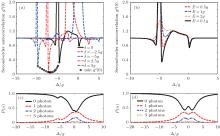
In this section, the influences of coupling strength V are the focus. The second-order autocorrelation function g²(0) and transmitted light of the driven cavity 〈 a^† a 〉 under different values of detuning Δ are shown in Figs.  1(a) and 1(b), with V = 0, 5g, 10g, respectively. When two QDs are uncoupled, only weak sub-Poissonian phenomenon g²(0) ≈ 0.99 is observed around Δ ≈ ± 2.6g. The shape of g²(0) is similar to that of the single QD– cavity system except detuning value.^[27] When two QDs are coupled, obvious second-order autocorrelation function dips corresponding to sub-Poissonian photon emission. For example, three dips occur at Δ ≈ 0.2g, − 4.5g, − 5.6g for V = 5g. These three points represent photon-blockade, corresponding to the three eigen-frequencies of the coupled system iV − γ and

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Second-order autocorrelation function and (b) cavity transmission 〈 a† a 〉 under different coupling strengths between QDs: V = 0 (solid line), V = 5g (dashed line), V = 10g (dash-dotted line). In the plot, g2(0) are truncated at 2 for a better view.

In Fig.  1(a), the open circles describe the variation of minimum g²(0) with Δ for specific QD coupling strength cases (between 4.6g and 10g), demonstrating a parabola-like shape. The lowest g²(0) ≈ 0.04 appears at V = 7g. We set g²(0) ≤ 0.5 as a criterion for effective single photon emission, and in the CDQDs– cavity scheme, QD coupling strength should be larger than 4.6g. For the cavity transmission shown in Fig.  1(b), an asymmetric scattering spectrum can be observed because of the coupling between QDs, and the location of the minimum photon numbers is consistent with that of V. With the increase of V, the distance between the two peaks increases while the skewing peak decreases. The increase of the distance can be explained through the frequency difference . The reduced peaks are caused by asymmetric eigenstates after the inducing of QDs coupling V, which is similar to the scenario of the atomic-cavity quantum electrodynamics.^[22] It can be predicted that if V is further increased, the curve will have nearly a single peak at Δ ≈ 0, which is a typical bare cavity resonance figure. Therefore QD coupling will weaken the QD– cavity interaction.

The values of g²(0) as a function of laser detuning under QD– cavity off-resonant condition are calculated with constant QDs coupling V = 5g. The QD– cavity detuning is defined as δ = ω _i − ω _c. As illustrated in Fig.  2(a), when δ is negative, the effects derived from QDs coupling and QD– cavity detuning compensate for each other. No obvious sub-Poissonian character is observed for δ = − 5g, and this case is similar to the case of V = 0 line in Fig.  1(a). When δ is positive, parabolic minimum g²(0) can be achieved due to both QD– cavity detuning and QDs coupling. The lowest second-order autocorrelation function g²(0) ≈ 0.04 appears at δ = 2g. We also investigate the probability of generating few photons P(n). The output photon state transmitted through the system can be recognized as the superposition of Fock states | ψ 〉 = ∑ _nc_n | n〉 , with P(n) = | c_n| ².^{[28, 29]} The values of g²(0) corresponding to different excitation amplitudes are depicted in Fig.  2(b). With the increase of E, the sub-Poissonian character fades, while the ultra-high super-Poissonian character around the resonant point decreases as well. In Figs.  2(c) and 2(d), the values of P(n) with and without QDs coupling (V = 5g) are calculated. The photon number distribution holds symmetry with the laser detuning in the uncoupled case. The detuning values for largest probability of one, two and three photons are about 1.6g, 1.2g, and 1.0g, respectively, which can be explained through the Jaynes– Cummings ladder. In the coupled QDs case, the symmetry is broken. Three peaks instead of two peaks are observed, corresponding to the three different eigenfrequencies discussed in the former part. The generations of one, two and three photons all reach their maximum values at an approximate detuning value of 0.65g. For the other two groups of peaks, the detuning values are discrete like the uncoupled one, but with smaller spacing. Therefore the coupling between QDs will affect the generation of few photons.

To further analyze the photon emission of CDQDs, the relationship between g²(0) and cavity decay rate is illustrated in Fig.  3. From strong coupling regime to weak coupling regime, we observe the photon statistics form sub-Poissonian to super-Poissonian, which is similar to the case of a typical single QD– cavity coupling system. When we extract the minimum g²(0) under different cavity decay rates and detunings, an interesting phenomenon is observed. The detuning positions for minimum g²(0) are discrete and can be divided into three regions: strong coupling, intermediate coupling, and weak coupling. In both strong coupling regime and weak coupling regime, strong sub-Poissonian character can be achieved with an altered laser frequency, which is different from the uncoupled QDs situation. In the intermediate coupling regime, we obtain very weak sub-Poissonian character, and detuning Δ is largely deviated from the former regime. When g > κ or g < κ , either QDs coupling or QD– cavity coupling will dominate the photon emission process, leading to strong sub-Poissonian. When g and κ are comparable, two coupling effects interfere with each other, leading to weak sub-Poissonian.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Second-order autocorrelation functions under (a) different QD– cavity detunings (E = 0.1g) and (b) different excitation amplitudes, with δ = 0; probabilities of n photon state P(n) (c) with QDs coupling and (d) without QDs coupling, with E = 2g and δ = 0.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Second-order autocorrelation as a function of cavity decay rate with the laser detuning Δ = − 4.5g. Inset: extracted minimum g2(0) under different cavity decay rates and at a corresponding detuning frequency. Squares represent the values of g2(0) and the circles denote the values of corresponding laser detuning.

We now transform the system Hamiltonian in a different basis: , and rewrite the Hamiltonian as H = H₁ + H₂

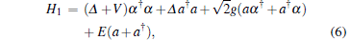Here, H₁ represents an off-resonant single QD– cavity system, and H₂ denotes a single QD. To investigate the relation between the two sets of Hamiltonian, g²(0) and cavity transmission between H and H₁ are compared in Figs.  4(a) and 4(b), respectively. The cavity transmission of CDQDs– cavity system is exactly the same as that of the modified single QD– cavity system, and photon emission of CDQDs– cavity is due to the interaction between an off-resonant QD– cavity and a single QD. Although the single QD does not contribute to the cavity photons, it influences the photon emission pattern of the system.

In the realistic system, the CDQDs– cavity coupling system is usually driven by optical pulse, which is discussed in this part. The Rabi frequency E is time dependent with Gaussian envelope, and given as

where Ω is the amplitude, t_p is the center time of the pulse, and is the 1/e times the half-width. In Fig.  5(a), the time evolution of the cavity field is calculated with the pulse parameters: Ω = 20g, t_p = 0.8/g, and τ = 0.2/g (indicating the pulse on a ns scale), other system parameters are the same as those in Fig.  1. The initialization state of the coupled system is vacuum field for cavity and ground state for QD. Therefore, the probabilities of generating few-photon P(n) value is time-dependent in the pulse excitation case. After the pulse impinging, P(n) rises and reaches a maximum value at around t = 1/g, which is delayed with respect to the pulse. After the pulse passes through, the cavity field will return to the vacuum state. We extract the P(n) at time t = 2t_p and plot them as a function of detuning Δ in Figs.  5(b) and 5(c), without and with QDs coupling (V = 5g), respectively. Again the asymmetric property caused by the QDs coupling is demonstrated, however the deviation from resonant point at a largest probability is larger than that from the continuous wave excitation. For pulse excitation, QDs– cavity system and optical pulse are overlapped in the frequency domain, therefore the detuning values are increased.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Comparison between two Hamiltonians: (a) second-order autocorrelation function and (b) cavity transmission, under V = 5g condition. The solid line denotes the original Hamiltonian in Eq.  (1), while the dashed line and circles refer to the modified Hamiltonian in Eq.  (6).

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) Time evolutions of probability of few-photon state. The normalized excitation pulse is plotted as dots. Probabilities of n photon state P(n) without (b) and with QDs coupling (c).

In the last part, we come to examine the robustness of our model. The situation that two QDs are not identical, is common in the QD fabrication. We mainly focus on the frequency differences between two QDs Δ ₂₁ = ω ₂ − ω ₁ and coupling strength differences between individual QD and cavity mode g₂/g₁. The QD spontaneous emission rate γ is ignored due to its small value. The curves of second-order autocorrelation function g²(0) under different values of Δ ₂₁ and g₂/g₁ are illustrated in Figs.  6(a) and 6(b), respectively. When frequencies of QDs mismatch, with the increase of ω ₂, the positions of lowest points shift toward the negative laser detuning, while strong sub-Poissonian statistics is maintained. In this respect, effects of QDs detuning Δ ₂₁ and QD– cavity detuning δ are similar, since they both modify the energy level of the coupling system and change the eigenfrequency of dress state. For mismatched coupling strength g₂/g₁, the positions of the g²(0) dips are slightly changed, while g²(0) value is varied. Surprisingly, when g₂ decreases, smaller minimum g²(0) is obtained. In Figs.  6(c) and 6(d), the curves of the second-order autocorrelation function g²(0) as a function of Δ ₂₁ and g₂/g₁ are plotted to examine the robustness of our scheme, at the detuning point Δ = − 4.5g. With the increase of Δ ₂₁, the sub-Poissonian character fades, however we can see that a small κ , namely strong coupling, can compensate for this negative effect. With the increase of g₂/g₁, g²(0) reaches its minimum at g₂/g₁ ≈ 1, namely when coupled QDs are identical. Sub-Poissonian character holds in most part, and the influence of cavity decay is not huge. Therefore, for two non-identical QDs, we still can achieve strong sub-Poissonian character in a large variation range.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Second-order autocorrelation function g2(0) under (a) different values of Δ 21 (g2 = g1) and (b) different values of g2/g1 (Δ 21 = 0). In the simulation we use κ = 20  GHz, g1 = 10  GHz, V = 50  GHz, E = 1  GHz. The values of g2(0) as a function of (c) Δ 21 and (d) g2/g1 at Δ = − 4.5g, with the parameters being the same as those in panels (a) and (b).

In this paper, the photon emission statistics and cavity transmission in a CDQDs– cavity system are numerically calculated, and the few-photon generations are discussed. Compared with uncoupled QDs, the CDQDs system can reach sub-Poissonian photon statistics in both strong and weak coupling regime. Choosing appropriate CDQDs– cavity detuning and QDs coupling, we can achieve a very small g²(0), indicating effective single photon emission. CDQDs also break the symmetry of the few-photon state generation under different laser detunings. The influences of cavity decay rate and laser frequency on the second-order autocorrelation function are considered. We reveal that the laser frequency detuning for minimum g²(0) under different cavity decay rates are discrete in CDQDs. Moreover, a modified model is proposed to explain the sub-Poissonian character. Finally, we discuss the robustness of our model and conclude that for the non-identical coupled QDs strong sub-Poissonian photon emission can still be achieved.