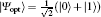Quantum Fisher information (QFI), which was initially introduced by Fisher, plays a critical role in quantum metrology.^[1] QFI characterizes the sensitivity of a state to change in a parameter.^[2] Moreover, QFI also has various applications in other quantum information tasks such as entanglement detection, ^[3] non-Markovianity characterization, ^[4] and investigation of uncertainty relations.^{[5, 6]}

Recently, great attention has been paid to the development of work on phase estimation addressing the practical problems of state decoherence.^{[7– 12]} In particular, the dynamics of QFI subjected to decoherence has attracted a great deal of attention.^{[13– 21]} More recently, enhancing the dynamics of QFI under decoherence by weak measurement (WM) and quantum measurement reversal (QMR) was reported.^[22] The authors found that that the QFI could be obviously enhanced by means of the WM and QMR in different regimes. Besides, the estimation of the quantum channel parameter for a two-qubit system with each qubit independently interacting with its Markovian environment has also been investigated.^[15] The authors studied the dynamics of QFI with respect to the decoherence rate and the interaction strength, and found that the QFI was not always enhanced by the increasing degree of entanglement in the input state. The dynamics of QFI in a two-level system coupled to a single bosonic reservoir has also been studied, ^{[4, 23, 24]} and some novel results have been found. In Ref.  [4], the authors investigated the evolution of QFI for a qubit coupled to a reservoir consisting of harmonic oscillators in the vacua, and unveiled the relations between the QFI flow and non-Markovianity for quantum dynamics in open systems. By using the hierarchy equation, some authors investigated the behaviors of two QFI quantities for a two-level system interacting with a zero-temperature bosonic reservoir, ^[23] and found that the dynamics of these two QFI quantities decayed with time almost monotonously in the weak-coupling limit and exhibited the oscillations and revivals in the strong-coupling limit. In particular, in Ref.  [24], the author discussed the non-Markovian effect on the dynamics of QFI for a qubit system subjected to a zero-temperature reservoir, and found that the evolution of QFI changed dramatically with the environment, and the revivals and retardation of QFI loss may occur by adjusting the cavity– qubit detuning.

In this paper, our main motivation comes from Ref.  [25] in which the authors studied the dynamics of a two-level system transversally coupled to multiple bosonic reservoirs. We extend the problem of parameter estimation in a two-level system from coupling with a single reservoir to coupling with multiple reservoirs. Our paper is different from those previous works.^{[4, 23, 24]} Their works are mainly concentrated on the dynamics of QFI for a qubit system coupled to a single bosonic reservoir, and the QFI decays with time almost monotonously in the weak coupling regime. Here, we study the dynamics of QFI for a two-level system which is surrounded by N zero-temperature reservoirs of field modes initially in the vacuum. Specifically, we compare the effects of reservoirs’ number N on the parameter estimation in both weak and strong coupling regimes for the two-level system coupled to multiple bosonic reservoirs. The results show that on one hand, the dynamics of QFI non-monotonically decays to zero with revival oscillations at some time in the weak coupling regime depending on the reservoirs’ parameters; on the other hand, the time evolution of QFI displays more quicker oscillations with increasing reservoir’ s number N in the strong coupling regime. The larger the reservoir’ s number N, the larger the amplitude of the QFI oscillation. Furthermore, we also present the relations between the QFI flow, the flows of energy and information, and the sign of the decay rate to gain insight into the physical processes characterizing the dynamics.

This paper is organized as follows: In Section 2, we introduce the model based on the two-level system coupled to multiple bosonic reservoirs and the definition of QFI. In Section 3, the QFI for the two-level system coupled to multiple bosonic reservoirs is investigated. Finally, we give the conclusion in Section 4.

In this paper, we consider a two-level system simultaneously coupled with N zero-temperature bosonic reservoirs. The total Hamiltonian is given by^[25]

where B = ∑ _kg_{n, k}b_{n, k}, g_{n, k} is the strength of the coupling between the two-level system and field mode k in the n-th reservoir, 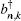and b_{n, k} are the mode k creation and annihilation operators, respectively, ω ₀ is the transition frequency of the atom, ω _{n, k} is the frequency of the k-th mode in the n-th reservoir, and σ ₊ = | 1〉 〈 0| and σ ₋ = | 0〉 〈 1| are the raising and lowering operators of the two-level system, respectively. The dynamics of the two-level system simultaneously coupled with N zero-temperature bosonic reservoirs is given by the reduced density matrix^{[25, 26]}

We assume N identical reservoirs with the Lorentzian spectral density

Here, the parameter λ defines the spectral width of the coupling, which is associated with the reservoir correction time by the relation τ _E = λ ^{− 1}, and the parameter γ is related to the relaxation time scale by the relation τ _R = γ ^{− 1}. With N identical system– reservoir coupling γ _n/λ _n = γ /λ , the corresponding probability amplitude C₁(t) is easily obtained as

with 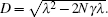According to Refs.  [27] and [28], the time-dependent decay rate is defined as

In the following, we investigate the precision of the parameter estimation for the two-level system coupled to multiple bosonic reservoirs using the widely accepted approach of QFI, which characterizes the sensitivity of the state with respect to changes in a parameter. The QFI is defined as^{[15, 29– 31]}

where ρ (θ ) is the density matrix of the system, θ is the parameter to be measured, and L is the symmetric logarithmic derivation given by

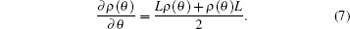By making use of the spectrum decomposition ρ (θ ) = ∑ _iλ _i| i〉 〈 i| , the QFI can be divided into two parts

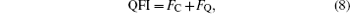where and .

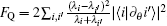
To estimate the parameter as precisely as possible, we should optimize the input state to maximize the QFI. Based on the model in this paper, the QFI-based parameter is assumed to be induced by a single qubit phase gate U(θ ) = | 0〉 〈 0| + exp(iθ )| 1〉 〈 1| acting on the two-level system. After the phase gate operation, consider the two-level system coupled to multiple bosonic reservoirs before the measurement is performed. 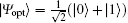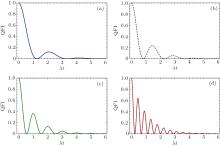To estimate the unknown parameter θ as precisely as possible, the optimal input state may be chosen as , which maximizes the QFI of the output state U(θ )| Ψ _opt〉 .^{[13, 32, 33]} With the output state U(θ )| Ψ _opt〉 and Eq.  (2), the reduced density matrix ρ (θ ) of the two-level system is given by

Before focusing on the effect of Markovian reservoirs’ number N on the QFI dynamics for the two-level system coupled to multiple bosonic reservoirs, we first review the case of a two-level system coupled to a single bosonic reservoir. As we know, the Markovian and the non-Markovian regimes are distinguished by the relation of the parameters γ and λ .^{[27, 28]} The γ < λ /2 (γ /λ < 1/2) represents the weak system– reservoir coupling regime, and γ > λ /2 (γ /λ > 1/2) corresponds to the strong system– reservoir coupling regime. However, in the presence of more than one reservoir, the system’ s dynamics would vary with N.^[25] If a two-level system is initially in contact with N Markovian reservoirs, each of which has γ _n < λ _n/2, then the system dynamics remains Markovian when 1 ≤ N < N₀ (N₀ = [λ _n/2γ _n + 1] ∈ Z), but becomes non-Markovian when N ≥ N₀. This physical origin can be understood as follows. When all the N identical reservoirs are in the weak coupling regime γ _n < λ _n/2 (γ _n/λ _n < 1/2), then 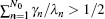is identical to the strong system– reservoir coupling regime. Therefore, N₀ can be regarded as a critical number of reservoirs in the sense of the condition γ _n < λ _n/2. To explore the influence of Markovian reservoirs N on the QFI for the two-level system coupled to multiple bosonic reservoirs, we compare the precision of the parameter estimation in both weak and strong coupling regimes. In particular, we are interested in the Markovian reservoirs which are all in the weak coupling regime γ _n < λ _n/2 (γ _n/λ _n < 1/2) and we shall mainly limit our study to this regime.

Now we consider the effect of Markovian reservoirs’ number N on the QFI dynamics for the two-level system coupled to multiple bosonic reservoirs. Figure  1 shows the QFI dynamics of the two-level system coupled to multiple bosonic reservoirs with the optimal input state in the weak coupling regime γ = 5λ /12 for different numbers of reservoirs N. When the system– reservoir coupling is γ = 5λ /12, the critical number of reservoirs is N₀ = 2. It can be seen that the dynamics of QFI monotonically decays to zero without revivals for N = 1. This result is consistent with the observations in Refs.  [4], [23], and [24], where a two-level system is coupled to a single zero-temperature bosonic reservoir. However, for N = 2, the dynamics of QFI non-monotonically decays to zero with small revival oscillations at some time even though the system– reservoir coupling strengths are all in the weak coupling regime γ = 5λ /12. With the Markovian reservoirs’ number N increasing, (e.g., N = 2, 4, 20), the QFI decays much more rapidly to zero accompanied with more revivals of the QFI. Based on the quantum estimation theory, this indicates that QFI characterizes the sensitivity of the state with respect to changes in a parameter, the revival of QFI means the optimal precision of estimation is increasing.

Fig.  1.

	Figure Option ViewDownloadNew Window
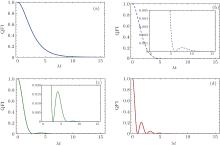	Fig.  1. QFI as a function of λ t with the optimal input state in the weak coupling regime γ = 5λ /12 for different numbers of reservoirs N: (a) N = 1, (b) N = 2, (c) N = 4, (d) N = 20.

In order to understand the physical origin of the non-monotonic behavior of the dynamics of QFI in the two-level system coupled to multiple bosonic reservoirs all in the weak coupling regimes, we present the relations between the QFI flow, the flows of energy and information, and the sign of the decay rate to gain insight into the physical processes characterizing the dynamics. We mainly investigate the effects of the Markovian reservoirs’ number N on the QFI flow, which is defined as the change rate of the QFI (QFI flow = ∂ QFI/∂ t). As shown in Ref.  [4], QFI flow < 0 denotes the flows of energy and information from the system to the environment, and QFI flow > 0 indicates that there is energy and information flows from the environment to the system. In Fig.  2, we plot the QFI flow as a function of λ t with the optimal input state 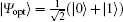in the weak coupling regime γ = 5λ /12 for different numbers of reservoirs N. When the system– reservoir weak coupling γ = 5λ /12, it can be seen that the QFI flow is always negative for N = 1. This indicates the loss of energy and information of the system to the reservoir. This result is consistent with the previous analysis in Ref.  [4]. However, for N ≥ 2, the QFI flow takes negative and positive values in this weak coupling regime. This phenomenon can be understood as the reversed flows of energy and information from the reservoirs to the system, and the system’ s non-Markovian dynamics emerges. Hence, the QFI displays oscillations and revivals.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. QFI flow as a function of λ t with the optimal input state 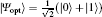in the weak coupling regime γ = 5λ /12, for different numbers of reservoirs N: (a) N = 1, (b) N = 2, (c) N = 4, (d) N = 20.

Besides, based on the present model, the time-dependent decay rate is given by Eq.  (5). By comparison of Figs.  2(a)– 2(d), it is easily verified that QFI flow < 0 corresponds to decay rate γ (t) ≥ 0, and QFI flow > 0 corresponds to a regime where the decay rate γ (t) takes negative values for some intervals of time. These results are consistent with the previous analysis in Refs.  [4] and [19], and indicate that 1 ≤ N < N₀, the decay rate γ (t) is always positive, while N ≥ 2, the decay rate γ (t) takes negative values for some intervals of time, and the system’ s non-Markovian dynamics emerges even though the system– reservoir couplings are all in the weak coupling regime. This indicates that the two-level system coupled to multiple bosonic reservoirs acts as a two-level system coupled to a single bosonic reservoir with a larger coupling constant.

Next, we show the QFI flow as a function of λ t and the reservoirs’ number N in the weak coupling region γ = 5λ /12 in Fig.  3. It can be seen that the QFI flow is positive within certain intervals of time. The positive values of the QFI flow imply the reversed flows of energy and information from the reservoirs back to the system, and the system’ s dynamics becomes non-Markovian.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. QFI flow as a function of λ t and the reservoirs’ number N with the optimal input state 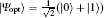in the weak coupling regime γ = 5 λ /12.

Finally, we also study the parameter estimation in the strong coupling regime using the QFI. Figure  4 shows the QFI dynamics of the two-level system coupled to multiple bosonic reservoirs with the optimal input state 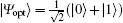in the strong coupling regime γ = 5λ . It can be seen that the dynamics of QFI non-monotonically decays to zero with revival oscillations at some time. The time evolution of QFI displays more quicker oscillations with increasing reservoir’ s number N (e.g., N = 1, 2, 4, 20) in the strong coupling regime. The larger the reservoir’ s number N, the larger the amplitude of the QFI oscillation. The oscillation of QFI with time implies that the precision of estimation may rise again in some time periods.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. QFI as a function of λ t with the optimal input state in the strong coupling regime γ = 5λ for different numbers of reservoirs N: (a) N = 1, (b) N = 2, (c) N = 4, (d) N = 20.

Some recent works studied the single environment reservoir effects on the non-Markovian dynamics of an open system, ^{[4, 23, 24]} few studies focused on the multiple environments on the dynamics of QFI in an open system. In this paper, we study the QFI for a two-level system coupled to multiple bosonic reservoirs. Unlike the previous analyses, ^{[4, 23, 24]} using QFI, here we mainly focus on the influence of the number of Markovian reservoirs N on the QFI dynamics. The results show that the dynamics of QFI non-monotonically decays to zero with revival oscillations at some time in the weak coupling regime depending on the reservoirs’ parameters. Furthermore, we also present the relations between the QFI flow, the flows of energy and information, and the sign of the decay rate to gain insight into the physical processes characterizing the dynamics. When N ≥ N₀, the decay rate of the two-level system takes negative values within certain intervals of time, corresponding to positive QFI flows. This indicates the reversed flows of energy and information from the reservoirs to the system. Moreover, our results show that the dynamics of QFI in the two-level system coupled to multiple bosonic reservoirs is similar to that in a two-level system coupled to a single bosonic reservoir in the strong coupling regime.