Cite this Article
Du Li-Jun, Song Hong-Fang, Li Hai-Xia, Chen Shao-Long, Chen Ting, Sun Huan-Yao, Huang Yao, Tong Xin, Guan Hua, Gao Ke-Lin. Determination of ion quantity by using low-temperature ion density theory and molecular dynamics simulation* . Chinese Physics B, 24(11): 113703  
Permissions
Determination of ion quantity by using low-temperature ion density theory and molecular dynamics simulation*
Du Li-Juna),b),c),d), Song Hong-Fanga),b),c),d), Li Hai-Xiaa),b),c),d), Chen Shao-Longa),b),c),d), Chen Tinga),b),c),d), Sun Huan-Yaoa),b),c), Huang Yaoa),b),c), Tong Xina),b),c), Guan Huaa),b),c), Gao Ke-Lina),b),c)
State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China
Key Laboratory of Atomic Frequency Standards, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China
Center for Cold Atom Physics, Chinese Academy of Sciences, Wuhan 430071, China
University of Chinese Academy of Sciences, Beijing 100049, China

†Corresponding author. E-mail: guanhua@wipm.ac.cn

*Project supported by the National Basic Research Program of China (Grant Nos. 2012CB821301 and 2010CB832803), the National Natural Science Foundation of China (Grant Nos. 11004222 and 91121016), and the Chinese Academy of Sciences.

Abstract

In this paper, we report a method by which the ion quantity is estimated rapidly with an accuracy of 4%. This finding is based on the low-temperature ion density theory and combined with the ion crystal size obtained from experiment with the precision of a micrometer. The method is objective, straightforward, and independent of the molecular dynamics (MD) simulation. The result can be used as the reference for the MD simulation, and the method can improve the reliability and precision of MD simulation. This method is very helpful for intensively studying ion crystal, such as phase transition, spatial configuration, temporal evolution, dynamic character, cooling efficiency, and the temperature limit of the ions.

Keyword: 37.10.Ty; 64.70.kp; 94.20.Fg; 52.65.Yy; ion crystal; ion quantity; low-temperature density model; molecular dynamics simulation
1. Introduction

In the bound state of an ion system, with the decrease in the average kinetic energy, ions will experience phase transitions from gas to liquid to solid state.[1, 2] An ion Coulomb crystal is of a solid state phase of strongly coupled and confined non-neutral ions with the same sign of charge, which can be formed in ion traps when the nearest neighboring Coulomb potential energy is 170  times larger than the average kinetic energy of the ions. Under such conditions, the ions’ maximum probability distribution and relative position present metastable features.[1– 3]

The ions’ mass-to-charge ratio, quantity, and temperature can be obtained by the dynamic process of ion crystal achieved by numerical calculations and compared with those of the three-dimensional ion crystal in a special plane obtained from experiments and numerical calculations.[4, 5] At the same time, the ion crystal may be imaged at arbitrary latitudes and three-dimensional information such as the distribution of micromotion, the distribution of the position and velocity vectors of any given ion in the whole ion crystal at any time can be achieved. Based on the dynamic trajectory model of an ion crystal, ion parameters of kinematic and dynamic temporal evolution can be tracked in the whole process of generation, trapping, crystallization, and equilibrium state of any given ion.[6, 7] By quantitatively manipulating the ions’ mechanical parameters of the numerical calculation, we can systematically study the different cooling and heating mechanisms and quantitatively demonstrate the cooling and heating efficiency.[8] By adopting the discrete Fourier transform of the parameters of temporal evolution of the ions’ position and velocity vectors, the characteristic frequency spectra of the ions’ micromotion and secular motion can be demodulated. When we compare the above results with the fluorescence spectra induced from the ions’ secular motion stimulation in the experiment, the trapping and structural parameters of the ion trap and the ions’ motional mode can be demonstrated.[9]

Although many characteristic parameters can be extracted by the dynamic calculation of the ion system, the whole calculation process strongly depends on the initial conditions and dynamic parameters. The ion quantity is one of the most fundamental and crucial input parameters and cannot be quantitatively evaluated from the experimental results. It needs to be adjusted and fed back repeatedly in the process of the dynamic calculation of ions, which requires a lot of time. However, in a quadrupole radio-frequency (RF) field, the spatial distribution property of an ion crystal can be represented by the ion low-temperature density model. Therefore, the ion quantity evaluated directly from the ion density and the size of the ion crystal can be used to solve the problem of the initial value of the ion quantity, which cannot be found in the MD simulation.

In this paper, we report a method by which the ion quantity is estimated rapidly, which is based on the lowtemperature ion density theory and combined with the size of the ion crystal obtained from experiment with the precision of a micrometer. The result is used as the reference input of the MD simulation and is adjusted slightly. When we compare the ion spatial structure calculated from the MD simulation and the image of ions captured by an electron-multiplying chargecoupled device camera (EMCCD), the matched ion quantity is found. The result is used to verify the consistency between the two theories and is the basis for studying other mechanisms of the ions by adopting the MD simulation.

2. Experimental setup

The linear Paul trap used in our experiment is shown in Fig.  1(a). A detailed description of the experimental setup can be found in Ref.  [10]. The linear trap consists of four parallel three-sectioned stainless-steel cylindrical electrode rods in a quadrupole configuration. The lengths of the central part (B) and the remaining parts (A, C) of each of the electrodes are 2z0 = 5.90  mm and 2ze = 24.00  mm, respectively, as indicated in Fig.  1(a). The diameter of each electrode rod is d = 8.00  mm, and the minimum distances between the trap axis and the electrodes are all r0 = 3.50  mm. The confinement of the ions in the radial plane is obtained by applying an RF field 1/2Urfcos(Ω rft) to the diagonal A1, B1, C1, and A3, B3, C3 electrode rods. At the same time, an RF field with opposite phase − 1/2Urfcos(Ω rft) to the diagonal A2, B2, C2, and A4, B4, C4 electrode rods is applied. The RF frequency can be varied from 3.50 to 4.50  MHz, and the output amplitude 1/2Urf can be adjusted from 40 to 200  V. The confinement of the ions in the axial direction is obtained by applying direct current (DC) voltage to the eight end parts of electrodes (A1, A2, A3, A4 and C1, C2, C3, C4) in a range of 0.010– 20.000  V.

The 40Ca+ ions are loaded by two-photon photoionization[11] of calcium atoms and subsequently Doppler laser cooled[12– 17] to a crystalline state by using a 397-nm cooling laser and an 866-nm repumping laser to excite the 42S1/2– 42P1/2 and 3d2D3/2– 4p2P1/2 transitions along the trap center (z) axis, respectively. The detection of the ions is performed by an imaging system with 13– 15 times magnification, which collects spontaneously emitted light at 397  nm during the laser cooling cycles to a photo-multiplier tube (PMT) and an EMCCD. Both of them are placed perpendicularly to the trap z axis to monitor the fluorescence intensity and position of the ions projected onto the y– z plane, respectively. A 245-μ m diameter optical fiber is inserted in the trap center and imaged for absolute calibration of the magnification of the microscopy lens at 13.31.

A pure 40Ca+ ion crystal is shown in Fig.  2, with Urf = 240  V and Uend = 2.000  V, captured by the EMCCD in the y– z plane. The Coulomb crystal with three-dimensional ellipsoid shape can be obtained from the rotational symmetry structure of the ion crystal around the trap (z) axis. By controlling Urf and Uend, the size of the ion crystal can be adjusted in radial and axial directions, represented as R and L, respectively.

Fig.  1. (a) Sketch of the linear Paul trap and RF potential. (b) Schematic of the laser, light-emitting diode (LED), and linear Paul trap setup.

Fig.  2. A pure 40Ca+ ion crystal captured by an EMCCD.

3. Evaluation of the ion quantity

In order to analyze the ion quantity of the ion crystal achieved in Fig.  2, we adopt the low-temperature density model and the MD simulation. Ion density spatial distribution is widely investigated in ion trap mass spectrometry to estimate the order of magnitude of the number of ions. High temperature and large volumetric errors lead to considerable uncertainty in the number of ions. Micrometer precision control and measurements of the ions’ feature parameters at mK temperatures are more meaningful, especially when combined with MD simulation.

3.1. Low-temperature density model

The motion of the ions in a long multipole ion trap is described as a motion in an effective electric potential expressed by[15]

where 2p denotes the number of poles. For p = 2, the effective electric potential is a quadrupole potential.

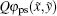
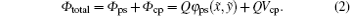The total potential energy of ions in a linear RF trap is given by the sum of the harmonic pseudo-potential energy and the ion plasma Coulomb interaction potential energy QVcp[16] as

The equilibrium ion density distribution n(r) in such a potential at temperature T is given by

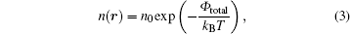from the Boltzmann distribution of kinetic energy, [17] where n0 and kB are the normalization and Boltzmann’ s constant, respectively.

Using Eq.  (2), equation  (3) can be rearranged as

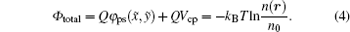The characteristics of ion density can be easily studied in the limit of either high or low temperature, which can be distinguished by the relation between the Debye length λ D = (kBTɛ 0/nQ2)1/2[17] and the spatial extent of the ion system. The ions can be regarded as low-temperature density systems whenever λ D is much smaller than the spatial extent of the ion system in which space charge plays a significant role. The ions in the linear Paul trap are Doppler laser cooled to plasma crystallization with a temperature of T < 10  mK and a Debye length of λ D = 0.6  μ m, which is much smaller than the inter-ion spacing of the Coulomb crystal and certainly smaller than the spatial extent of the ion crystal following the low-temperature limit. The kinetic energy of the ions is ∼ 1× 10− 25  J, which is about a hundred thousand times less than the electric potential energy from the ion plasma Coulomb interaction and the harmonic pseudo potential energy. Therefore, the kinetic energy can be neglected to some extent. For kBT ≈ 0, the condition that n(r) is finite requires that

which can be explained as the fact that the Coulomb interaction potential caused by the ion distribution must exactly counterbalance the effect of the trap potential, [18] and the force Fion on each ion of the crystal should be zero in equilibrium. To obtain the local density distribution of the ion crystal, we must solve the potential self-consistently by the use of Poisson’ s equation in the ion crystal,

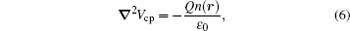subject to the boundary conditions that specify the value of Φ total on the trap electrodes. Here, ɛ 0 is the permittivity of a vacuum. Combining Eqs.  (1), (5), and (6), we obtain the density of the ion crystal as

In a quadrupole (p = 2) ion trap at T ≈ 0, equation  (7) can be described as

which is the constant ion distribution and is only related to RF frequency and amplitude. Therefore, a high-precision number of ions can be obtained by controlling and measuring both the RF and the volume of ions in a high accuracy.

An ion crystal is a cylindrically symmetric ellipsoidal Coulomb plasma with principal axes Rx = Ry = R and L in the x-, y-, and z-directions as shown in Fig.  2, owing to the cylindrical symmetry of the potential. The number of ions obtained by multiplying the cold ion density with volume 4π R2L/3 is about 305(10). The error in the ion quantity is assessed to be less than 4% and is mainly due to the inaccuracy of volume measurements and demarcation of the magnification imaging system. Figure  3 shows a detailed shape measurement of the ion crystal in Fig.  2 with Uend varying from 1.000 to 13.500  V, when Ω rf = 2π × 3.715  MHz and Urf = 240  V. Figure  3(a) shows the relation between the sizes of the principal axes R and L of the ellipsoidal Coulomb crystals and Uend. Figure  3(b) shows that the volumes and number of ions in the ellipsoidal Coulomb crystals keep nearly unvaried with Uend, owing to the fact that the density of ions given by Eq.  (8) is independent of Uend and constant.

Fig.  3. Detailed shape measurements of single-component crystals containing about 305(10) 40Ca+ ions in a group of different Uend values. (a) Relation between the sizes of the principal axes 2R and 2L of the ellipsoidal Coulomb crystals and Uend. (b) The volumes and number of ions in the ellipsoidal Coulomb crystals keep nearly unvaried with Uend.

3.2. MD simulation

The MD simulation is always used to track the temporal evolutions of position and velocity vectors of all ions, and they are developed from the numerical solution of the classical dynamic equations.[19, 20] The ions trapped in a linear Paul trap are a strong Coulomb interaction system, whose motion can be described by classical dynamics and satisfy the Ehrefest criterion. The motion can be expressed as

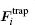
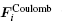
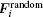
where i = 1, ..., N is the ion’ s ordinal number, and Mi, ri, and υ i are the mass, position and velocity vectors, respectively. The ions will feel four forces in a Paul trap. They are trapping potential force , Coulomb interaction force , random collision , and laser light interaction force . The trapping force, given by

is a physical quantity related to the trapping parameters, such as the size of the ion trap, geometrical factors, the radial RF field, and the direct current (DC) potential. Qi is the charge of the i-th ion. The trapping field is expressed as follows:

where Ω rf is the frequency of the applied RF field (with amplitude Urf), Uend is the DC potential, η = 0.26513(7) is a constant related to the trap geometry, [10] 2z0 is the length of the axial trapping electrodes, and r0 is the minimum distance from the trap axis to each of the electrodes.

The i-th ion feels the Coulomb interaction force from all other ions and can be expressed as follows:

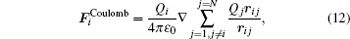where ri j is the distance between the i-th and j-th ions, ri j is the unit vector, and ɛ 0 is the vacuum permittivity. This is the process of an N-body interaction.

The is the random collision force, which is the physical quantity related to background pressure, residual gas components, and stray potential.[21] It cannot be described by a unified formula. Since the effect for the ion is equivalent to one isotropous random heating force, the force is equivalent to an increase factor with a constant rate in the simulation.

The force of the laser is

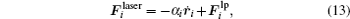which is equivalent to a combined force of linear resistance and laser radiation force. The resistance coefficient α i is a physical quantity related to a laser power density and frequency detuning. When the laser is red detuned, the laser will cool the ion, and the resistance force is negative. When the laser is blue detuned, the laser will heat the ion, and the resistance force is positive. The laser radiation force is related to the direction of propagation and power density of the laser. Since the cooling laser is usually split into two beams which radiate the ion from two opposite directions with the same power densities, the combined laser radiation force is zero.

In the process of the ion dynamic evolution, the RF trapping force and the long-distance Coulomb interaction between ions are dominant. The micromotion of ions will heat ions through the Coulomb interaction between ions. Other forces will affect the ions, too. However, the force depends on the ion temperature.

In order to quantitatively describe the dynamic temporal evolution, the ion dynamic temporal process will be split into equal time intervals in the numerical calculation, and the dynamic equations will be established and solved for all ions at any moment. The time interval of the adjacent moment is called the time step Δ t of the numerical calculation. When we solve the equations of position and velocity vectors at the next moment, the position and velocity vectors at the present moment and those at the last moment are used as initial values, and a Taylor expansion with four-order accuracy should be adopted in the approximation. In this process, half of a time step 1/2Δ t is the time interval, and the position and velocity vectors of all ions are calculated alternately at all moments. In this calculation process, the position and velocity vectors of all ions will be calculated alternately with a 1/2Δ t time interval, analogous to two alternately leaping frogs. Therefore, this numerical calculation is called the “ Leap Frog” algorithm.[22– 24]

In order to reflect the micromotion of ions, the precision of time step Δ t is much less than the RF period in the dynamic calculation of the trapped ion crystal. Considering the limit of computer RAM, the calculating step Δ t is chosen to be 1/30 of an RF period at about 8.97  ns. The ion quantity is one of the most important input parameters, and it determines the complexity of the dynamic calculation, the spatial structure, the distance between ions, the cooling efficiency of ions, and the temperature limit of ions. In the process of the MD simulation calculation, the estimated value of ion quantity 305(10) obtained from the low-temperature density model is the input factor, and the parameter of ion quantity is adjusted within a small range. Based on the resolution of 0.60  μ m in both experiment and simulation, the coincidence levels of the images obtained from the MD simulation and the EMCCD are checked, including the size, shape, distribution, distance, and ion quantity in the projection plane. Here, the best match pictures can be achieved. At the same time, the evaluated results and errors of ion quantity can be achieved from the low-temperature density model and the MD simulation, respectively. In Fig.  4, a comparison among the different pictures is given, where the results in Fig.  4(a) are obtained from the experiment and those in Figs.  4(b)– 4(d) are obtained from the MD simulation. When the ion quantity is 306(8), the MD simulation result is best matched with the experimental results. Therefore, the ion number is 306(8), which is consistent with the result obtained directly from the low-temperature density model above. Final evaluation of the ion quantity can be given as 306(10) from the average of these two results. Compared with repeatedly adjusting the initial ion quantity in the MD simulation, the method of combining the low-temperature density model and MD simulation is very efficient.

Fig.  4. Comparison between the experimental result and the MD simulation with different ion quantities. (a) The experimental result; (b) the MD simulation result with an ion quantity of 306; (c) the MD simulation result with an ion quantity of 296; (d) the MD simulation result with an ion quantity of 316. When the ion quantity is 306(8), the MD simulation results are best matched with the experimental results.

4. Conclusions and outlook

The preliminary result of ion quantity for an ion crystal with mK temperatures is found from the low-temperature density model and is the input value of ion quantity in the MD simulation. This method can improve the efficiency, calculation reliability, and accuracy of the MD simulation. The precision of the final evaluation is controlled to better than 4%, and the two theories are compatible. In addition, the measurement reliabilities of the RF field, DC voltages, pixel resolution of the EMCCD, and geometric factors of the ion trap are confirmed. This work is the basis for more detailed studies on spatial structure, phase transition, motional and dynamic properties, cooling efficiency, temperature limit, and more in ion crystals.

Acknowledgment

We would like to thank Shi Ting-Yun for our fruitful discussion.

Reference
1 Slattery W L, Doolen G D and Dewiit H E 1980 Phys. Rev. A 21 2087 DOI:10.1103/PhysRevA.21.2087 [Cited within:2]
2 Mitchell T B, Bollinger J J, Dubin D H E, Huang X P, Itano W M and Baughman R H 1998 Science 282 1290 DOI:10.1126/science.282.5392.1290 [Cited within:1]
3 Schmöger L, Versolato O O, Schwarz M, Kohnen M, Windberger A, Piest B, Feuchtenbeiner S, Gutierrez J P, Leopold T, Micke P, Hansen A K, Baumann T M, Drewsen M, Ullrich J, Schmidt P O and López-Urrutia J R C 2015 Science 347 1233 DOI:10.1126/science.aaa2960 [Cited within:1]
4 Germann M, Tong X and Willitsch S 2014 Nat. Phys. 10 820 DOI:10.1038/nphys3085 [Cited within:1]
5 Ostendorf A, Zhang C B, Wilson M A, Offenberg D, Roth B and Schiller S 2006 Phys. Rev. Lett. 97 243005 DOI:10.1103/PhysRevLett.97.243005 [Cited within:1]
6 Ulm S, Roβnagel J, Jacob G, Degünther C, Dawkins S T, Poschinger U G, Nigmatullin R, Retzker A, Plenio M B, Schmidt-Kaler F and Singer K 2013 Nat. Commun. 4 2291 DOI:10.1038/ncomms3290 [Cited within:1]
7 Pyka K, Keller J, Partner H L, Nigmatullin R, Burgermeister T, Meier D M, Kuhlmann K, Retzker A, Plenio M B, Zurek W H, Campo A D and Mehlstäubler T E 2013 Nat. Commun. 4 2291 DOI:10.1038/ncomms3291 [Cited within:1]
8 Takashi B and Izumi W 2002 J. Appl. Phys. 92 4109 DOI:10.1063/1.1506005 [Cited within:1]
9 Roth B, Blythe P and Schiller S 2007 Phys. Rev. A 75 023402 DOI:10.1103/PhysRevA.75.023402 [Cited within:1]
10 Du L J, Chen T, Song H F, Chen S L, LI H X, Huang Y, Tong X, Guan H and Gao K L 2015 Chin. Phys. B 24 083702 DOI:10.1088/1674-1056/24/8/083702 [Cited within:2]
11 Chen T, Du L J, Song H F, Liu P L, Huang Y, Tong X, Guan H and Gao K L 2014 Chin. Phys. B 23 123702 DOI:10.1088/1674-1056/23/12/123702 [Cited within:1]
12 Wineland D J, Drullinger R E and Walls F L 1978 Phys. Rev. Lett. 40 1639 DOI:10.1103 [Cited within:1]
13 Neuhauser W, Hohenstatt M, Toschek P and Dehmelt H G 1978 Phys. Rev. Lett. 41 233 DOI:10.1103 [Cited within:1]
14 Hänsch T W and Schawlow A L 1975 Opt. Commun. 13 68 DOI:10.1016/0030-4018(75)90159-51975 [Cited within:1]
15 Gerlich D 1992 Adv. Chem. Phys. 82 1 DOI:10.1002/9780470141397.ch1 [Cited within:1]
16 Champenois C 2009 J. Phys. B 42 154002 DOI:10.1088/0953-4075/42/15/154002 [Cited within:1]
17 Wineland D J, Bollinger J J, Itano W M and Prestage J D 1985 J. Opt. Soc. Am. B 2 1721 [Cited within:3]
18 Dehmelt H G 1968 Adv. At. Mol. Phys. 3 53 DOI:10.1016/S0065-2199(08)60170-0 [Cited within:1]
19 Prestage J D, Williams A, Maleki L, Djomehri M J and Harabetian E 1991 Phys. Rev. Lett. 66 2964 DOI:10.1103/PhysRevLett.66.2964 [Cited within:1]
20 Zhang C B, Offenberg D, Roth B, Wilson M A and Schiller S 2007 Phys. Rev. A 76 012719 DOI:10.1103/PhysRevA.76.012719 [Cited within:1]
21 Kielpinski D, King B E, Myatt C J, Sackett C A, Turchette Q A, Itano W M, Monroe C and Wineland D J 2000 Phys. Rev. A 61 032310 DOI:10.1103/PhysRevA.61.032310 [Cited within:1]
22 Verlet L 1967 Phys. Rev. 159 98 DOI:10.1103/Physrev.159.98 [Cited within:1]
23 Verlet L 1968 Phys. Rev. 165 201 DOI:10.1103/PhysRev.165.201 [Cited within:1]
24 Zhang M Q and Skeel R D 1995 J. Comput. Chem. 16 365 DOI:10.1002/jcc.540160309 [Cited within:1]