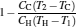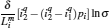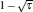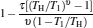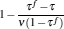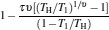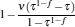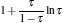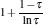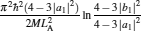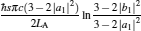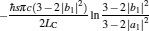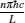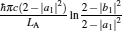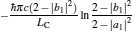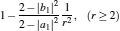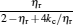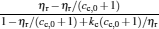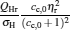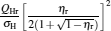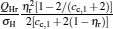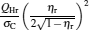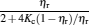Cite this Article
Huang Chuan-Kun, Guo Jun-Cheng, Chen Jin-Can. Performance characteristics of low-dissipative generalized Carnot cycles with external leakage losses* . Chinese Physics B, 24(11): 110506  
Permissions
Performance characteristics of low-dissipative generalized Carnot cycles with external leakage losses*
Huang Chuan-Kuna), Guo Jun-Chengb), Chen Jin-Cana)
Department of Physics, Xiamen University, Xiamen 361005, China
College of Physics and Information Engineering, Fuzhou University, Fuzhou 350002, China

†Corresponding author. E-mail: junchengguo@qq.com

Corresponding author. E-mail: jcchen@xmu.edu.cn

*Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11405032).

Abstract

Under the assumption of low-dissipation, a unified model of generalized Carnot cycles with external leakage losses is established. Analytical expressions for the power output and efficiency are derived. The general performance characteristics between the power output and the efficiency are revealed. The maximum power output and efficiency are calculated. The lower and upper bounds of the efficiency at the maximum power output are determined. The results obtained here are universal and can be directly used to reveal the performance characteristics of different Carnot cycles, such as Carnot heat engines, Carnot-like heat engines, flux flow engines, gravitational engines, chemical engines, two-level quantum engines, etc.

Keyword: 05.70.Ln; 05.20.–y; generalized Carnot cycle; low-dissipation; unified model; performance characteristic
1. Introduction

Thermodynamic cycles are of great importance not only in theory but also in practice.[1– 8] The Carnot heat engine is one of the most important models in thermodynamics.[9, 10] Generalized Carnot cycles have been widely used in the various fields in physics.[11– 13] Investigations on the maximum power output of Carnot heat engines and other Carnot cycles and the efficiency at the maximum power output have attracted a great deal of attention during the last few decades and is a hot research topic.[14– 17] Recently, Esposito et al. established a new cycle model of Carnot heat engines on the basis of the weak dissipation assumption.[16] They proved that the efficiency of low-dissipative Carnot heat engines at the maximum power output is located between η C/2 and η C/(2 − η C), while the Curzon– Ahlborn efficiency[18]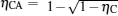 can be derived under the so-called symmetric dissipation, where η C is the Carnot efficiency. On the basis of Ref.  [16], low-dissipation assumption has been successfully used in the models of other thermodynamic cycles such as Carnot refrigerators, [19, 20] Carnot chemical engines, [21] two-level quantum Carnot cycles, [22] etc. Many significant results have been obtained from the various low-dissipative cycle models, but the common characteristics of these cycles have been rarely revealed. On the other hand, the external leakage losses of thermodynamic cycles are one of the main sources of irreversible losses, [23– 25] but these losses have not been included in the existing low-dissipative cycle models. Thus, it is of great significance to establish a unified model of low-dissipative generalized Carnot cycles with external leakage losses and reveal the general performance characteristics of these cycles.

The rest of the present paper is organized as follows. In Section 2, generalized Carnot cycles are briefly introduced and some examples are given. In Section 3, the model of low-dissipative generalized Carnot cycles with external leakage losses is proposed and the expressions of the power output and the efficiency are derived. In Section 4, the optimal relations between the power output and the efficiency are obtained. In Section 5, the maximum power outputs of cycles operated under different conditions are calculated and the bounds of the efficiency at the power output are determined. In Section 6, the performance characteristics related to the maximum efficiency are also discussed. In Section 7, the performance characteristics of the low-dissipative Carnot heat engine with heat leakage losses are directly obtained from the universal results. Finally, some important conclusions are drawn in Section 8.

2. Generalized Carnot cycles

As is well known, heat engines operated in different temperature fields are able to produce useful work and thermodynamic cycles operated in other potential fields such as the chemical potential field, pressure field, gravitational field, quantum field, etc. are also able to obtain useful work. When thermodynamic cycles are operated in a potential field only including two reservoirs, which may be described by two parameters XH and XC (XH > XC), they are usually referred to as generalized Carnot cycles as shown in Fig.  1. Such cycles include four processes, where two processes exchange energy with two reservoirs and the other two processes do not exchange energy with two reservoirs, and can be taken as the models of some heat engines, [13– 18, 26– 28] flux flow engines, [29– 31] gravitational engines, chemical engines, [32– 35] two-level quantum engines, [36– 41] etc. For example, for a Carnot heat engine, XH and XC correspond to the temperatures TH and TC of high- and low-temperature heat reservoirs; for non-Carnot heat engines, [26– 28] which include the Otto cycle, [42, 43] Brayton cycle, [44– 46] Diesel cycle, [47, 48] and Atkinson cycle, [49, 50]XH and XC correspond to the highest temperature TH and lowest temperature TC of the working substance; for Carnot-like engines such as a gravitational engine, which may be regarded as an abstract model of hydropower stations or tidal power plants, XH and XC correspond to the height HH and HC of high- and low-gravitational potential energy reservoirs. For different types of engines, the parameters corresponding to XH and XC are listed in Table  1, where η r, g is the reversible efficiency of generalized Carnot cycles. Some signs in Table  1 are explained as follows. The F(S1, S2) is the total entropy change varying with the spin angular momenta Si = 〈 Ŝ z〉 (i = 1, 2), [51– 53]CH and CC are the heat capacities of the working substance during two heat exchange processes of non-Carnot heat engines, [26, 27, 41]Tj (j = 1, 2) are the initial temperatures of the working substance in two heat exchange processes, and “ + ” and “ − ” in signs “ ± ” correspond to the cases of j = 1 and 2, respectively. The reversible efficiencies η r, g of such heat engines and the efficiencies η r, m at the maximum work output[41] are listed in Table  2, where τ = TC/TH, ν = CP/CV, and f = 1/(1 + ν ). 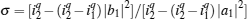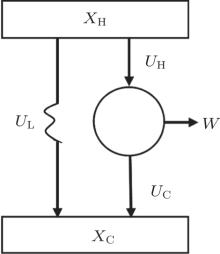The pH = | a1| 2 and pC = | b1| 2 are the probabilities of two different superposed states in the eigenstate | ϕ 1(L)〉 , and , where in (n = 1, 2) is the quantum number of the system, δ , m, and q are three positive parameters, and Li (i = H, C) is the width of the potential field. For the different values of δ , m, and q, two-level quantum engines have different eigenenergies and reversible efficiencies, which are listed in Table  3.[36– 41]

Fig.  1. Schematic diagram of a generalized Carnot cycle with external leakage losses between two reservoirs.

Table 1. Parameters Xi (i = H, C) and Uir (i = H, C), and reversible efficiency η r, g of generalized Carnot cycles with different potential fields.[41]
Table 2. Expressions of reversible efficiency η r, g of several non-Carnot heat engines and the efficiency η r, m at the maximum work output.[26, 27, 40]
Table 3. Expressions of ɛ n, UHr, UCr, and η r, g for two-level quantum Carnot engines with different quantum fields.[36– 41]
3. Unified cycle model

Under the low-dissipation assumption, [16] for an irreversible generalized Carnot cycle operated between two different potential energy reservoirs, the energies absorbed from the high-potential energy reservoir and released into the low-potential energy reservoir by the working substance per cycle can be expressed respectively as

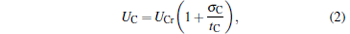where UHr and UCr, whose expressions are also listed in Table  1, are the exchange energies between the working substance and the two potential energy reservoirs when the reversible cycle is carried out, σ H and σ C are two parameters containing the concrete irreversibility, tH and tC are, respectively, the time durations in which the working substance contacts with the high- and low-potential energy reservoirs. This assumption means that compared with energy transfer times tH and tC, the relaxation time of the working substance in the cycle is very fast, and that, by ignoring complicated time-dependent terms due to the non-equilibrium between the reservoirs and the working substance, energy dissipations are expected to behave as σ H/tH and σ C/tC along high- and low-potential energy segments of the cycle. It is seen from Eqs.  (1) and (2) that the cycle will return to reversibility when tH → ∞ and tC → ∞ . Compared with tH and tC, the times spent in two processes without energy exchange are further assumed to be negligible. Thus, the time spent in finishing one cycle may be approximately expressed as t = tH + tC.

Usually, the external leakage losses inevitably occur between two potential energy reservoirs and will affect the performance of the cycle. The external leakage losses per cycle UL shown in Fig.  1 may be simply described by

where uL is the rate of the external leakage losses from the high-potential energy reservoir to the low-potential energy reservoir. In general, uL is dependent on the energy reservoir and will have different values for different energy reservoirs. However, uL can be regarded as a constant for given energy reservoirs. Using Eqs.  (1)– (3), we can derive the power output P and the efficiency η of the generalized Carnot cycle with the external leakage losses as

Using Eqs.  (4) and (5), one can discuss the performance characteristics of low-dissipative generalized Carnot cycles with external leakage losses between the two reservoirs.

4. Optimal relations between power output and efficiency

In order to obtain the optimal relations between the power output and the efficiency of low-dissipative generalized Carnot cycles with external leakage losses, we introduce the Lagrangian function

where λ is the Lagrangian multiplier. By using Eq.  (6) and the Euler– Lagrange equations ∂ L/∂ tH = 0 and ∂ L/∂ tC = 0, an important relation

is obtained. Equation  (7) can be solved as

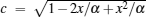
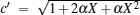
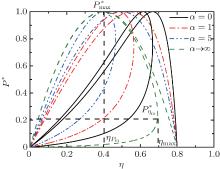
where , , α = σ C/σ H, x = tH/σ H, and X = tC/σ C. By substituting Eq.  (8) into Eqs.  (4) and (5), both the power output and the efficiency can be expressed as functions of x or X, namely,

where η r, g= 1 − UCr/UHr, k = uLσ H/UHr, and K = uLσ C/UHr. By using Eqs.  (9) and (10), the general characteristic curves of the power output varying with the efficiency can be generated with the help of a numerical calculation, as shown in Fig.  2, where the controlling parameter is x or X, P* = P/Pmax is the normalized power output, and the parabolic-shaped and loop-shaped curves correspond to the cases of k = 0 or K = 0, and k ≠ 0 or K ≠ 0, respectively. When 0 < α < ∞ , k = α k, and consequently, the first and second equations in Eq.  (9) or (10) are equivalent to each other. When α = 0 or α → ∞ , both k and K may have the same values because they correspond to different curves, respectively.

Fig.  2. Curves of the dimensionless power output P* versus η for different values of α , where η r, g= 0.8, and k = 0 and 0.02. When α → ∞ , the value of K is chosen to be equal to that of k, respectively.

It can be clearly seen from Fig.  2 that when the external leakage losses between two reservoirs are negligible, the η – P* characteristic curves are parabolic. The power output is equal to zero when the efficiency reaches the reversible efficiency η r, g. When the influence of external leakage losses between two reservoirs is considered, the η – P* characteristic curves become looped shapes. The maximum efficiency η max is smaller than η r, g, and the power output at the maximum efficiency is larger than zero. For a given value of k or K, the efficiency at the maximum power output increases with the decrease of α , and for a given value of α , the efficiency at the maximum power output with external leakage losses between two reservoirs is always smaller than that without external leakage losses. 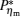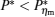Figure  2 also shows that when the efficiency is smaller than η Pm, the power output of generalized Carnot cycles decreases with the decrease of the efficiency, and when the power output is smaller than , the efficiency of the generalized Carnot cycle also decreases with the decrease of power output. Obviously, the regions of and η < η Pm are not optimal for the generalized Carnot cycle. Thus, the optimal regions of generalized Carnot cycles should be and η max ≥ η ≥ η Pm. According to the two criteria given above, we can further determine the optimal regions of x and X as xη m ≥ x≥ xPm and Xη m ≥ X≥ XPm, from which we can directly give the optimal criteria of tH and tC as xη mσ H ≥ tH ≥ xPmσ H and Xη mσ C ≥ tC ≥ XPmσ C, where xPm and XPm are the values of x and X at the maximum power output and xη m and Xη m are the values of x and X at the maximum efficiency, respectively, xPm, XPm, xη m, and Xη m will be given by some equations of Sections 5 and 6.

It is significant to note that for some special values of α , some simple expressions of the power output and efficiency may be directly derived from Eqs.  (9) and (10). For instance, when α → 0 and σ H is finite, the power output and the efficiency can be expressed as

When α = 1, i.e., σ H = σ C, the power output and the efficiency are given by

which correspond to the so-called symmetric dissipation.[16] When α → ∞ and σ C is finite, the power output and the efficiency can be obtained as

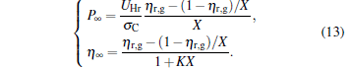5. Efficiency at the maximum power output

From Eq.  (9) and dP/dη = 0, it can be proved that when

the power output attains its maximum, i.e.,

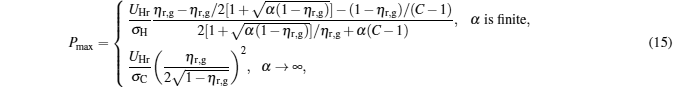and the corresponding efficiency is given by

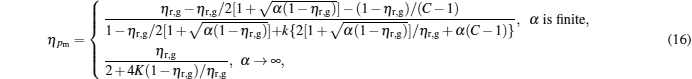where

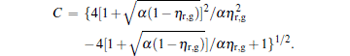
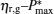
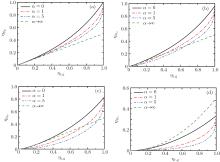
By using Eqs.  (15) and (16), the and η r, g– η Pm curves for different values of k or K can be plotted as shown in Figs.  3 and 4, respectively.

Fig.  3. Curves of the maximum power output 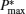versus reversible efficiency η r, g for different values of α .

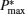
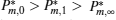
Figure  3 shows that decreases with the increased value of α in the same value of η r, g, namely, , which means that can be regard as the limit of the maximum power output. From Fig.  4(a), it can be identified that η Pm, 0 and η Pm, ∞ are the upper and lower bound of the efficiency at the maximum power output without external leakage losses between the two reservoirs. In this condition, for any other specific value of α , η Pm, others is restricted between η Pm, 0 and η Pm, ∞ . It is seen from Figs.  4(b)– 4(d) that the curves with k ≠ 0 or K ≠ 0 decline with the increase of external leakage losses, but the decreasing rate of the curve of η Pm, ∞ is smaller than that of the others, which leads to η Pm, ∞ > η Pm, 0 as shown in Fig.  4(d). In other words, η Pm, 0 may be regarded as the upper bound of the efficiency at the maximum power output when external leakage losses are not obvious. When external leakage losses increase, the efficiency at the maximum power output will decrease and η Pm, ∞ will replace η Pm, 0 as the upper bound of the efficiency at the maximum power output. Figure  4 also shows that η Pm, 0 with k = 0 is always larger than any other efficiency at the maximum power output and is the upper bound of the efficiency at the maximum power output for the low-dissipative generalized Carnot cycle with external leakage losses.

Fig.  4. Variations of the efficiency at the maximum power output with reversible efficiency η r, g for different values of α and k, where (a) k = 0, (b) k = 0.01, (c) k = 0.05, and (d) k = 0.5. In panels  (a)– (d), when α → ∞ , the value of K is chosen to be equal to that of k, respectively.

Besides, for some special values of α , the expressions of the maximum power output and the corresponding efficiency can be obtained by using Eqs.  (15) and (16). For example, when α → 0, the maximum power output and the corresponding efficiency can be simplified into

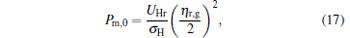When α = 1, the maximum power output and the corresponding efficiency are derived as

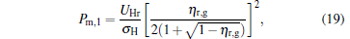When α → ∞ , the maximum power output and the corresponding efficiency are given by

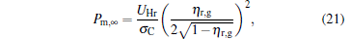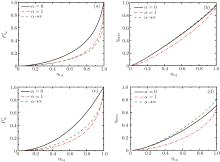
6. Power output at maximum efficiency

It can be found from Fig.  2 that there exists not only a maximum power output but also a maximum efficiency for the generalized Carnot cycles with external leakage losses. According to Eq.  (10) and dη /dP = 0, one can derive a relation as

For general cases, we can obtain the values xη m and Xη m of x and X at the maximum efficiency by using Eq.  (23) and the numerical calculation. For some special values of α , equation  (23) is solvable. For example, when α = 0, we obtain

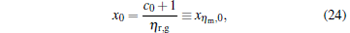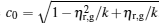
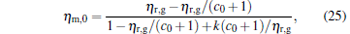where . The maximum efficiency and the corresponding power output can be expressed as

When α = 1, the solution is given by

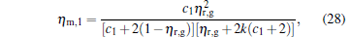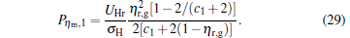where . The maximum efficiency and the corresponding power output can be expressed as

For α → ∞ , from the second equation of Eq.  (23), we derive

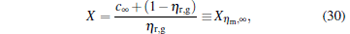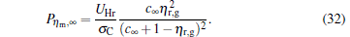where . The maximum efficiency and the corresponding power output can be expressed as

By using the above equations, the and η r, g– η max curves can be generated as shown in Fig.  5. The positions of these curves depend on not only the value of α but also the value of k or K.

Fig.  5. Variations of the maximum efficiency and the corresponding power output with reversible efficiency η r, g for different values of α and k: k = 0.01 ((a) and (b)) and k = 0.1 ((c) and (d)). In panels  (a)– (d), when α → ∞ , the value of K is chosen to be equal to that of k, respectively.

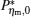
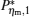
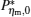
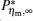
Figures  5(a) and 5(c) show that when k = K = 0.01 and k = K = 0.1, is larger than and . It can be proved from Eqs.  (26) and (32) that is larger than for any finite value of k = K. Thus, we can take as the upper bound of the power output at the maximum efficiency. It is found from Fig.  5(b) that when the external leakage losses are not obvious, i.e. the value of k or K is very small, the efficiencies of generalized Carnot cycles satisfy η r, g ≈ η m, ∞ ≈ η m, 0. Comparing Fig.  5(b) with Fig.  5(d), it is noted that the curves of η max decline with the increase of external leakage losses for a given value of α , and the decreasing rate of the curve of α → ∞ is smaller than those of other curves, which leads to η m, ∞ > η m, 0 when external leakage losses are large enough.

7. Discussion

By using the results obtained above and Tables  1– 3, we can directly discuss the performance characteristics of various generalized Carnot cycles. For example, for a low-dissipative Carnot heat engine with heat leakage losses between the two heat reservoirs, we can obtain the performance characteristics of the heat engine as long as one chooses UH = QH, UC = QC, UL = QL, UHr = QHr = THΔ S, UCr = QCr = TCΔ S, and uL = qL, where Δ S is the entropy change of the working substance in the isothermal heat exchange process and qL is the rate of the heat leakage losses between two heat reservoirs. For some special values of α , we easily obtain the analytical expressions of the maximum power output Pmax and the corresponding efficiency η Pm, and the maximum efficiency η max and the corresponding power output Pη m of the low-dissipative Carnot heat engine with heat leakage losses, which are listed in Table  4, where kc = qLσ H/QHr, Kc = qLσ C/QHr, and η r, g= 1 − TC/TH ≡ η r. If the heat leakage losses between two heat reservoirs are negligible, the optimal relations between the power output and the efficiency can be further simplified into

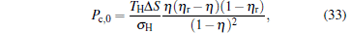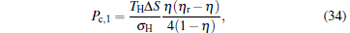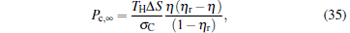which are exactly the results obtained in Refs.  [21] and [41]. The efficiency at the maximum power output is given by

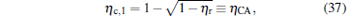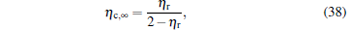respectively, which are the results obtained in Ref.  [16]. For other kinds of low-dissipative generalized Carnot cycles with external leakage losses, similar discussion may be carried out by using the above universal results and Tables  1– 3.

Table 4. Expressions of some parameters of the low-dissipative Carnot heat engine with heat leakage losses for different values of α .

Entropy production is often taken as an objective function in thermodynamic cycle optimizations.[54– 56] According to the above analyses, one can derive the entropy production per cycle for a low-dissipative Carnot heat engine as

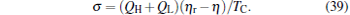It is seen from Eq.  (39) that when η = η r, then σ = 0. This means that if the maximum efficiency of a system can attain the Carnot efficiency, the state of the minimum entropy production corresponds to that of the maximum efficiency. If the maximum efficiency of a system is smaller than the Carnot efficiency, the minimum entropy production depends on both η and (QH + QL), and consequently, the state of the minimum entropy production is different from that of the maximum efficiency. Using Eq.  (39), one can further obtain the relation between the entropy production rate and the power output as

It is seen from Eq.  (40) that the entropy production rate depends on both the efficiency and the power output. Thus, the state of the minimum entropy production rate is, in general, different from that of the maximum power output.

8. Conclusions

We have established the model of low-dissipative generalized Carnot cycles with external leakage losses, which may include several classes of typical engines, such as Carnot heat engines, Carnot-like engines, Carnot chemical engines, two-level quantum Carnot engines, etc. The expressions of the power output and efficiency are derived, and the optimal relations between them are discussed. The optimal operating regions are determined. The performance characteristics at the maximum power output and efficiency are analyzed. It is also expounded that like the efficiency and power output, the entropy production may be taken as an objective function of a thermodynamic system. There exist some certain relations between the entropy production and the efficiency and between the entropy production rate and the power output, but for general cases, the state of the minimum entropy production is different from that of the maximum efficiency and the state of the minimum entropy production rate is different from that of the maximum power output. The results obtained are universal, from which not only some important conclusions in the literature may be derived but also some novel results can be obtained.

Reference
1 Linke H, Humphrey T E, Löfgren A, Sushkov A O, Newbury R, Taylor R P and Omling P 1999 Science 286 2314 DOI:10.1126/science.286.5448.2314 [Cited within:1]
2 Blickle V and Bechinger C 2012 Nat. Phys. 8 143 DOI:10.1038/nphys2163 [Cited within:1]
3 Fialko O and Hallwood D W 2012 Phys. Rev. Lett. 108 085303 DOI:10.1103/PhysRevLett.108.085303 [Cited within:1]
4 He J, Li Cong and Zhang Y 2013 Chin. Phys. Lett. 30 100501 DOI:10.1088/0256-307X/30/10/100501 [Cited within:1]
5 Zhang Y and He J 2013 Chin. Phys. Lett. 30 010501 DOI:10.1088/0256-307X/30/1/010501 [Cited within:1]
6 Xiao Y, He J and Cheng H 2014 Acta Phys. Sin. 63 200501in Chinese DOI:10.7498/aps.63.200501 [Cited within:1]
7 Li J, Chen L, Ge Y and Sun F 2013 Acta Phys. Sin. 62 130501in Chinese DOI:10.7498/aps.62.130501 [Cited within:1]
8 Liu N, Luo X and Zhang M 2014 Chin. Phys. B 23 080502 DOI:10.1088/1674-1056/23/8/080502 [Cited within:1]
9 Cheng X T and Liang X G 2015 Chin. Phys. B 24 060510 DOI:10.1088/1674-1056/24/6/060510 [Cited within:1]
10 van den Broeck C 2005 Phys. Rev. Lett. 95 190602 DOI:10.1103/PhysRevLett.95.190602 [Cited within:1]
11 Esposito M, Lindenberg K and van den Broeck C 2009 Phys. Rev. Lett. 102 130602 DOI:10.1103/PhysRevLett.102.130602 [Cited within:1]
12 Esposito M, Lindenberg K and van den Broeck C 2009 Europhys. Lett. 85 60010 DOI:10.1209/0295-5075/85/60010 [Cited within:1]
13 Izumida Y and Okuda K 2012 Europhys. Lett. 97 10004 DOI:10.1209/0295-5075/97/10004 [Cited within:2]
14 Izumida Y and Ito N 2013 Eur. Phys. J. B 86 431 DOI:10.1140/epjb/e2013-40569-1 [Cited within:1]
15 Tu Z C 2012 Chin. Phys. B 21 020513 DOI:10.1088/1674-1056/21/2/020513 [Cited within:1]
16 Esposito M, Kawai R, Lindenberg K and van den Broeck C 2010 Phys. Rev. Lett. 105 150603 DOI:10.1103/PhysRevLett.105.150603 [Cited within:5]
17 Sheng S and Tu Z C 2013 J. Phys. A: Math. Theor. 46 402001 DOI:10.1088/1751-8113/46/40/402001 [Cited within:1]
18 Curzon F L and Ahlborn B 1975 Am. J. Phys. 43 22 DOI:10.1119/1.10023 [Cited within:2]
19 de Tomás C, Hernández A C and Roco J M M 2012 Phys. Rev. E 85 010104 DOI:10.1103/PhysRevE.85.010104 [Cited within:1]
20 Wang Y, Li M, Tu Z C, Hernández A C and Roco J M M 2012 Phys. Rev. E 86 011127 DOI:10.1103/PhysRevE.86.011127 [Cited within:1]
21 Guo J, Wang Y and Chen J 2012 J. Appl. Phys. 112 103504 DOI:10.1063/1.4765725 [Cited within:2]
22 Guo J, Wang J, Wang Y and Chen J 2013 J. Appl. Phys. 113 143510 DOI:10.1063/1.4799795 [Cited within:1]
23 Gordon J M 1991 Am. J. Phys. 59 551 DOI:10.1119/1.16818 [Cited within:1]
24 Izumida Y, Okuda K, Hernández A C and Roco J M M 2013 Europhys. Lett. 101 10005 DOI:10.1209/0295-5075/101/10005 [Cited within:1]
25 Chen J 1994 J. Phys. D: Appl. Phys. 27 1144 DOI:10.1088/0022-3727/27/6/011 [Cited within:1]
26 Leff H S 1987 Am. J. Phys. 55 602 DOI:10.1119/1.15071 [Cited within:3]
27 Land sberg P T and Leff H S 1989 J. Phys. A: Math. Gen. 22 4019 DOI:10.1088/0305-4470/22/18/034 [Cited within:1]
28 Zhang Y, Lin B and Chen J 2005 J. Appl. Phys. 97 084905 DOI:10.1063/1.1885186 [Cited within:2]
29 Bejan A 1996 Int. J. Heat Mass Transfer 39 1175 DOI:10.1016/0017-9310(95)00209-X [Cited within:1]
30 Chen L, Bi Y and Wu C 1999 J. Phys. D: Appl. Phys. 32 1346 DOI:10.1088/0022-3727/32/12/310 [Cited within:1]
31 Hu W and Chen J 2006 J. Phys. D: Appl. Phys. 39 993 DOI:10.1088/0022-3727/39/5/014 [Cited within:1]
32 De Vos A 1991 J. Phys. Chem. 95 4534 DOI:10.1021/j100164a065 [Cited within:1]
33 Gordon J M and Orlov V N 1993 J. Appl. Phys. 74 5303 DOI:10.1063/1.354253 [Cited within:1]
34 Lin G, Chen J and Brück E 2004 Appl. Energ. 78 123 DOI:10.1016/j.apenergy.2003.07.001 [Cited within:1]
35 Xia S, Chen L and Sun F 2009 J. Appl. Phys. 105 124905 DOI:10.1063/1.3151964 [Cited within:1]
36 Bender C M, Brody D C and Meister B K 2000 J. Phys. A: Math. Gen. 33 4427 DOI:10.1088/0305-4470/33/24/302 [Cited within:2]
37 Abe S 2011 Phys. Rev. E 83 041117 DOI:10.1103/PhysRevE.83.041117 [Cited within:1]
38 Abe S and Okuyama S 2011 Phys. Rev. E 83 021121 DOI:10.1103/PhysRevE.83.021121 [Cited within:1]
39 Abe S and Okuyama S 2012 Phys. Rev. E 85 011104 DOI:10.1103/PhysRevE.85.011104 [Cited within:1]
40 Wang J and He J 2012 J. Appl. Phys. 111 043505 DOI:10.1063/1.3681295 [Cited within:1]
41 Guo J, Wang J, Wang Y and Chen J 2013 Phys. Rev. E 87 012133 DOI:10.1103/PhysRevE.87.012133 [Cited within:5]
42 Ge Y, Chen L and Sun F 2008 Appl. Energy 85 618 DOI:10.1016/j.apenergy.2007.09.008 [Cited within:1]
43 Chen L, Zheng T, Sun F and Wu C 2003 Int. J. Ambient Energy 24 195 DOI:10.1080/01430750.2003.9674923 [Cited within:1]
44 Zhang Y, Ou C, Lin B and Chen J 2005 J. Energy Res. Technol. 128 216 DOI:10.1115/1.2213272 [Cited within:1]
45 Zhou Y, Tyagi S K, Wu C and Chen J 2005 Int. J. Ambient Energy 26 37 DOI:10.1080/01430750.2005.9674969 [Cited within:1]
46 Wu C and Kiang R L 1990 Int. J. Ambient Energy 11 129 DOI:10.1080/01430750.1990.9675167 [Cited within:1]
47 Chen L, Lin J, Luo J, Sun F and Wu C 2002 Int. J. Energy Res. 26 965 DOI:10.1002/(ISSN)1099-114X [Cited within:1]
48 Zhao Y, Lin B, Zhang Y and Chen J 2006 Energy Convers. Manage. 47 3383 DOI:10.1016/j.enconman.2006.01.008 [Cited within:1]
49 Zhao Y and Chen J 2006 Appl. Energy 83 789 DOI:10.1016/j.apenergy.2005.09.007 [Cited within:1]
50 Ge Y, Chen L, Sun F and Wu C 2007 J. Energy Inst. 80 52 DOI:10.1179/174602207X174540 [Cited within:1]
51 Geva E and Kosloff R 1992 J. Chem. Phys. 97 4398 DOI:10.1063/1.463909 [Cited within:1]
52 Geva E and Kosloff R 1992 J. Chem. Phys. 96 3054 DOI:10.1063/1.461951 [Cited within:1]
53 Wu F, Chen L, Wu S, Sun F and Wu C 2006 J. Chem. Phys. 124 214702 DOI:10.1063/1.2200693 [Cited within:1]
54 Cheng X and Liang X 2013 Chin. Phys. B 22 010508 DOI:10.1088/1674-1056/22/1/010508 [Cited within:1]
55 Zhou B, Cheng X and Liang X 2013 Chin. Phys. B 22 084401 DOI:10.1088/1674-1056/22/8/084401 [Cited within:1]
56 Wang W, Cheng X and Liang X 2013 Chin. Phys. B 22 110506 DOI:10.1088/1674-1056/22/11/110506 [Cited within:1]