Cite this Article
Xie Qi, Hu Bin, Chen Ke-Fei, Liu Wen-Hao, Tan Xiao. Chaotic maps and biometrics-based anonymous three-party authenticated key exchange protocol without using passwords* . Chinese Physics B, 24(11): 110505  
Permissions
Chaotic maps and biometrics-based anonymous three-party authenticated key exchange protocol without using passwords*
Xie Qi, Hu Bin, Chen Ke-Fei, Liu Wen-Hao, Tan Xiao
Hangzhou Key Laboratory of Cryptography and Network Security, Hangzhou Normal University, Hangzhou 311121, China

†Corresponding author. E-mail: qixie68@126.com

Corresponding author. E-mail: whl819_819@163.com

*Project supported by the Natural Science Foundation of Zhejiang Province, China (Grant No. LZ12F02005), the Major State Basic Research Development Program of China (Grant No. 2013CB834205), and the National Natural Science Foundation of China (Grant No. 61070153).

Abstract

In three-party password authenticated key exchange (AKE) protocol, since two users use their passwords to establish a secure session key over an insecure communication channel with the help of the trusted server, such a protocol may suffer the password guessing attacks and the server has to maintain the password table. To eliminate the shortages of password-based AKE protocol, very recently, according to chaotic maps, Lee et al. [2015 Nonlinear Dyn.79 2485] proposed a first three-party-authenticated key exchange scheme without using passwords, and claimed its security by providing a well-organized BAN logic test. Unfortunately, their protocol cannot resist impersonation attack, which is demonstrated in the present paper. To overcome their security weakness, by using chaotic maps, we propose a biometrics-based anonymous three-party AKE protocol with the same advantages. Further, we use the pi calculus-based formal verification tool ProVerif to show that our AKE protocol achieves authentication, security and anonymity, and an acceptable efficiency.

Keyword: 05.45.Vx; 05.45.–a; chaos; Chebyshev chaotic maps; anonymous; authenticated key exchange
1. Introduction

With the rapid development of network and communication technologies, more and more users make transactions via accessing remote networks. In order to obtain the trusted services, the user and the remote server should authenticate each other and establish the common session key before transactions. Since communicating parties can use their low-entropy and human-memorable password to authenticate each other via an insecure network and establish a session key in password-based authenticated key exchange (AKE) protocol, therefore, password-based AKE protocol is convenient and fast, and many such protocols have been proposed.[1– 5] Specifically, due to the merits of chaos theory related to cryptography, such as S-boxes design, [6] encryption, [7– 9] and hash functions, [10] many chaotic-maps-based two-party and three-party password authenticated key exchange schemes have been addressed.[11– 18]

In 2011, Yoon and Jeon[16] showed that a first chaotic-maps-based three-party password authenticated key exchange (3PAKE) protocol proposed by Wang and Zhao[17] cannot resist illegal message modification attack, and then they proposed an improved one. Unfortunately, these two protocols have a weakness that the server and the two users should share a long-term secret key, respectively. Thus, the two users have to protect the long-term secret keys. Later, based on enhanced Chebyshev chaotic map, Lai et al.[18] proposed a novel 3PAKE protocol, but their protocol is vulnerable to the privileged insider attack and the off-line password guessing attack.[19] After that, Lee et al.[20] proposed a chaotic-maps-based anonymous 3PAKE scheme, but their scheme is vulnerable to the man-in-the-middle attack since an inside attacker can easily obtain the users’ identities.[21, 22] In the same year, Xie et al.[23] proposed a chaotic-maps-based 3PAKE protocol without using a timestamp. In 2014, Lai et al.[24] proposed a provably-secure 3PAKE scheme by using Chebyshev chaotic maps in the standard model. All the above mentioned protocols are based on a server public key or smart card, or both to protect the user passwords. To eliminate the shortages of using a server public key and smart card, Farash and Attari[25] proposed a first chaotic-maps-based 3PAKE protocol without using a server public key, nor smart card nor symmetric cryptosystems in 2014, but Xie et al.[26] demonstrated that their protocol cannot resist impersonation attack nor off-line password guessing attack, and then they proposed an improved chaotic-maps-based 3PAKE protocol with the same advantages to overcome the weaknesses of Farash and Attari’ s protocol. In 2015, Shu[27] also showed that Farash and Attari’ s scheme is vulnerable to off-line password guessing attack and suffers communication burden, and proposed an improved one.

Very recently, Lee et al.[28] pointed out that password-based AKE protocol may suffer the password guessing attacks and the server has to maintain the password table. Therefore, Lee et al. proposed a first three-party-authenticated key exchange scheme without using passwords to eliminate the shortages of the password-based AKE protocol, and claimed its security by providing a well-organized BAN logic test. However, in this paper, we demonstrate that their protocol cannot resist any impersonation attack. Compared with the protocol of using a password, the user’ s biometric has many advantages, for example, it cannot be lost nor forgotten nor shared nor copied easily, and it is difficult to fabricate or distribute and guess.[28] Therefore, to overcome the security weaknesses of Lee et al.’ s protocol, by using chaotic maps, we propose a biometrics-based anonymous three-party AKE protocol with the same advantages. Further, we show that our AKE protocol achieves authentication, security and anonymity by using the pi calculus-based formal verification tool ProVerif.

The rest of the paper is organized as follows. In Section  2, we review Chebyshev chaotic maps. Then, we review and cryptanalyse Lee et al.’ s protocol in Sections  3 and 4. In Section  5, we propose a biometric-based 3AKE protocol. After that, security analysis and the performance comparison are presented in Sections  6 and 7. Finally, some conclusions are drawn from the present study in Section  8.

2. Chebyshev chaotic maps

In this section, we introduce the Chebyshev polynomial and Chebyshev chaotic map.

Definition 1 (Chebyshev polynomial and semi-group property) Let n be an integer, and x ∈ [− 1, 1], then the Chebyshev polynomial Tn(x) : [− 1, 1] → [− 1, 1] will be defined as

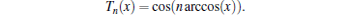
Therefore, the Chebyshev polynomial has the following recurrence relation:

where n ≥ 2.

Let r and s be integers, then Chebyshev polynomials will have the following semi-group property:

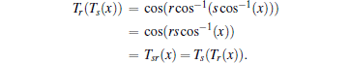
In 2008, Zhang[7] proved that the semi-group property defined on interval (− ∞ , + ∞ ) hold, that is,

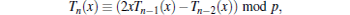
where n ≥ 2, x ∈ (− ∞ , + ∞ ), and p is a large prime number. Therefore,

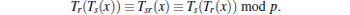
Definition 2 (chaotic map) When n > 1, Chebyshev polynomial map Tn(x) : [− 1, 1] → [− 1, 1] of degreen is a chaotic map with its invariant density 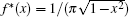, for positive Lyapunov exponent lnn.

The existing AKE protocols using chaotic maps are all based on the following two assumptions.

Definition 3 (chaotic-maps-based discrete logarithm problem) Given x and y, it is intractable to find the integer s, such that Ts(x) = y.

Definition 4 (chaotic-maps-based Diffie– Hellman problem) Given x, Tr(x), and Ts(x), it is intractable to find Trs(x).

3. Review of Lee et al.’ s protocol

The notations used in this paper are summarized as follows: S: a trusted server; i: the user; IDi: user i’ s identity; Bi: user i’ s biometrics; h(): a chaotic-maps-based secure one-way hash function; k: S’ s secret key; (x, Tk(x)): S’ s public key; Tk(IDi): user i’ s certificate issued by the server; EK()/DK(): secure symmetric encryption/decryption functions with key K; H(): BioHashing; ⊕ : the bitwise XOR operation; | | : the concatenation operation; p: a large prime number.

The details of Lee et al.’ s protocol are as follows.

Step 1 User  A chooses a, and computes KAS = TaTk(IDA) where Tk(IDA) is user A’ s certificates issued by the server. NA = Ta (IDA), HA = h(NA | | IDA| | IDB), NAB = Ta (IDB), CA = EKAS (IDA| | IDB| | HA| | NAB), and then the user sends m1 = {NA, CA} to B.

Step 2 Upon receiving m1 from A, B chooses b, and computes KBS = TbTk(IDB) where Tk(IDB) is User  B’ s certificates issued by the server. NB = Tb(IDB)HB = h(NB| | IDB), CB = EKBS(IDB| | HB| | NB), and then B sends m2 = {m1, NB, CB} to S.

Step 3 Upon receiving m2 from B, S first computes

and then S checks whether HA = h(NA| | IDA| | IDB) and HB = h(NB| | IDB) are correct. If not, S terminates this request. Otherwise, S computes

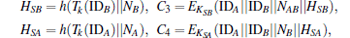
where Tk(IDA) and Tk(IDB) are users A and B’ s certificates. Finally, S sends m3 = {C3, C4} to B.

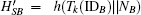
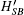
Step 4 Upon receiving m3, B decrypts C3 by KBS and obtains {IDB, IDA, NAB, HSB}, then computes and checks whether equals HSB. If not, he terminates it. Otherwise, B computes SK = Tb(NAB) = TbTa(IDB) and HBA = h(SK| | C4), and sends m4 = {HBA, C4} to A.

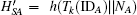
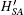
Step 5 When A obtains m4, he decrypts C4 by KAS and obtains {IDA, IDB, NB, HSA}, then computes and checks whether equals HSA. If not, he terminates it. Otherwise, A computes SK = Ta (NB) = TaTb(IDB) and verifies whether h(SK| | C4) = HBA. If not, he terminates it. Otherwise, A computes and sends m5 = h(SK| | IDA| | NAB) to B, and generates the session key SK′ = h(SK).

When B receives m5, he can check the validity of m5. If not, he rejects it. Otherwise, he also generates the session key SK′ = h(SK).

4. Security evaluation of Lee et al.’ s protocol

In this section, we will show that the Lee et al.’ s protocol cannot resist any impersonation attack, and discuss why their protocol suffers this attack.

4.1. Impersonation attack

Any legitimate user (e.g., User  C) can know other legitimate users’ identities if he has participated in the three-party AKE process with other users (e.g., Users  A and B). Then he can launch the impersonation attacks.

If a legitimate User  C wants to impersonate the User  A to establish a session key with the User  B, he can do the following steps.

Step 1 The C chooses a1 and uses his certificate Tk(IDC) issued by the server to compute KA1S = Ta1Tk(IDC)NA1 = Ta1(IDC), HA1 = h(NA1| | IDA| | IDB), NA1B = Ta1(IDB), CA1 = EKA1S(IDA| | IDB| | HA1| | NA1B), and then C sends m1 = {NA1, CA1} to B.

Step 2 Upon receiving m1 from A (impersonated by C), B chooses b and computes KBS = TbTk(IDB)NB = Tb(IDB), HB = h(NB| | IDB), CB = EKBS(IDB| | HB| | NB) and then B sends m2 = {m1, NB, CB} to S.

Step 3 Upon receiving m2 from B, S first computes

Obviously, IDA, IDB, HA1 and HB are valid. Therefore, S computes

where Tk(IDA) and Tk(IDB) are Users  A and B’ s certificates. Finally, S sends m3 = {C3, C4} to B.

Step 4 Upon receiving m3, B decrypts C3 by KBS and obtains {IDB, IDA, NA1B, HSB}. Obviously, HSB is valid. Then B computes SK1 = Tb(NA1B) = TbTa1(IDB) and HBA = h(SK1| | C4), and sends m4 = {HBA, C4} to A (C can intercept the message).

Step 5 When C intercepts the message m4, he decrypts C4 by KA1S and obtains {IDA, IDB, NB, HSA}, C does not need to verify the validity of HSA, but to compute SK1 = Ta1(NB) = Ta1Tb(IDB) and verifies whether h(SK1| | C4) = HBA. If not, he terminates it. Otherwise, C computes and sends m5 = h(SK1| | IDA| | NA1B) to B, and generates the session key SK1′ = h(SK1). Obviously, B can check the validity of m5 and obtains the session key SK1′ = h(SK1).

That is, the impersonation attack is a success.

4.2. Discussion

Lee et al.’ s protocol cannot resist any impersonation attack, the reason is that the server cannot authenticate whether the communicating parties (e.g., Users  A and B) are legitimate. As a cryptographic protocol, each communicating party should hold a secret key, which is shared with the trusted server, and then they authenticate each other by the shared secret key. However, in Lee et al.’ s protocol, each communicating party except the server seems to have no secret key.

When we come to analyze Lee et al.’ s protocol, the server authenticates User  A (or B) by checking whether HA = h(NA| | IDA| | IDB) (or HB = h(NB| | IDB)) is correct in Step 3. However, even if the equation holds, it cannot guarantee the validity of the User  A, because IDA and (KAS ∈ [0, p − 1], NA ∈ [0, p − 1]) has no necessary correlation, the server cannot authenticate Tk(IDA) from KAS = TaTk(IDA) either due to the different a values in each session run and chaotic-maps-based discrete logarithm problem. That is to say, it is indistinguishable for different TaiTk(IDi)(i = 1, 2, … ) generated by different users (including the adversary), anyone who knows IDi and Tk(IDj), (j ≠ i or j = i.) can impersonate the user i to generate the authentication message that can pass through the authentication process of the server S.

Therefore, Lee et al.’ s protocol is vulnerable to impersonation attack.

5. The proposed protocol

The proposed protocol consists of three phases: system setup phase, registration phase, authentication and key exchange phase.

5.1. System setup phase

The server S chooses a large prime number p, its public key (x ∈ Zp, Tk(x) mod p) and secret key k based on Chebyshev chaotic maps, a chaotic-maps-based one-way hash function h() and a biohashing H(), secure symmetric encryption/decryption functions EK()/DK() with key K.

Finally, S keeps the secret key k and publishes the parameters {p, x, Tk(x), h(), H()}.

5.2. Registration phase

User i chooses his identity IDi, sends IDi and registration information to S via a secure channel.

After receiving IDi and the registration information from the user i, the server S first checks the validity of user i’ s real personal information, e.g., personal identification card, then computes ei = h(IDi | | k), wherek is a secret key kept by S, and stores {IDi, ei, p, x, Tk(x), h(), H()} into a smart card and sends it to the useri via a secure channel.

When the User  i receives the smart card, he scans and enters his personal biometrics Bi. It is worth mentioning that no one can obtain Bi except the user i, and the biometrics scanner can be combined in the smart card reader. The user i computes Ri = H(Bi | | IDi), fi = h(Ri) and TIDi = Ri⊕ ei = H(Bi | | IDi)⊕ h(IDi | | k), and stores fi and TIDi into his smart card.

5.3. Authentication and key exchange phase

In this phase, Users  A and B can authenticate each other and establish a session key with the help of the trusted server S. Algorithm 1 illustrates this phase.

Step 1 User  A inserts his smart card into a device, inputs his biometrics BA, then the smart card computes RA = H(BA | | IDA) and checks whether fA = h(RA) holds. If not, it terminates the computation. Otherwise, the smart card chooses a large positive integer a, computes eA = RA⊕ TIDA = h(IDA | | k), KAS = TaTk(x)HA = h(Ta(x)| | IDA| | IDB| | eA), and CA = EKAS(IDA| | IDB| | HA| | Ta(x)). Then it sends m1 = {Ta(x), CA} to B.

Step 2 Upon receiving m1 from A, B inserts his smart card into a device, inputs his biometrics BB, then the smart card computes RB = H(BB | | IDB) and checks whether fB = h(RB) holds. If not, it terminates the computation. Otherwise, the smart card chooses a large positive integer b, computes eB = RB⊕ TIDB = h(IDB | | k), computes KBS = TbTk(x)HB = h(Tb(x)| | IDB| | eB), and CB = EKBS(IDB| | HB| | Tb(x)). Then B sends m2 = {m1, Tb(x), CB} to S.

Step 3 Upon receiving m2 from B, S first computes

Then, S checks whether the decrypted Ta(x) and Tb(x) are the same as the received ones. If not, it rejects the request. Otherwise, S computes , , , and , and checks whether and . If so, S computes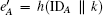

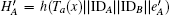
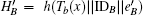
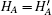
and sends m3 = {C3, C4} to B. Otherwise, S terminates this request.

Step 4 Upon receiving m3, B decrypts C3 by KBS and obtains {IDB, IDA, Ta(x), HSB}, then computes 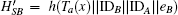and checks whether equals HSB. If not, he terminates it. Otherwise, B computes SK = TbTa(x) and HBA = h(SK| | IDB| | IDA| | C4), and sends m4 = {HBA, C4} to A.

Step 5 When A obtains m4, he decrypts C4 by KAS and obtains {IDA, IDB, Tb(x), HSA}, then computes 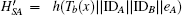and checks whether equals HSA. If not, he terminates it. Otherwise, A computes SK = TaTb(x) and verifies whether h(SK| | IDB| | IDA| | C4) = HBA. If not, he terminates it. Otherwise, A computes and sends m5 = h(SK| | IDB| | IDA) to B, and generates the session key SK′ = h(TaTb(x)).

Step 6 When B receives m5, he verifies whether m5 = h(SK| | IDB| | IDA). If it does not hold, B terminates it. Otherwise, A and B share the session key SK′ = h(TaTb(x)).

6. Security analyses

In this section, we will show that the proposed scheme is safe.

6.1. Formal verification

In order to prove the security of a protocol, researchers always use the formal security proof or the formal verification. The former is presented by artificial structure, the weaknesses are that the structure process is complex and difficult, and the errors may not be easy to find; while the latter is performed automatically, and the errors can be detected easily. On the other hand, the formal verification tool ProVerif[29] is based on applied pi calculus, [30] which uses Dolev– Yao model[31] and supports many cryptographic primitives such as symmetric and asymmetric encryption, digital signature, hash function, etc., and can be used to analyze the security, authentication and anonymity of cryptographic protocols automatically and effectively. Therefore, we use ProVerif to analyze our protocol.

The formal definition of our proposed protocol can be divided into three parts: the declaration part, the process part, and the security property part. The declaration part includes the definitions of communication channels, variables, functions and other components used in the protocol.

There are two types of channels in the formal model: a public channel c for communicating general protocol messages and two private channels for communicating smart card data between users and their smart cards. These channels are defined as follows:

free c: channel,

free sca: channel [private],

free scb: channel [private].

The variables and constants used in the protocol are defined as follows:

free SKAB: channel [private],

free SKBA: channel [private],

free IDA: bitstring,

free IDB: bitstring,

free IDV: bitstring,

const p: bitstring,

const x: bitstring,

const k: bitstring [private],

const BA: bitstring [private],

const BB: bitstring [private].

Among them, BA and BB correspond to Users  A and B’ s biometrics respectively. IDV is used for verifying the anonymity property. According to the protocol, other variables and constants are obvious.

The functions used in the protocol are defined as follows:

fun h(bitstring): bitstring,

fun H(bitstring): bitstring,

fun xor(bitstring, bitstring): bitstring,

fun T(bitstring, bitstring): bitstring,

fun senc(bitstring, bitstring): bitstring.

Here, function h and function H represent hash functions in the protocol, and function T represents the Chebyshev polynomial. The algebraic properties of these functions are modeled as the following equations and reduction:

equation forall a: bitstring, b: bitstring; T(T(x, b), a) = T(T(x, a), b),

equation forall m: bitstring, n: bitstring; xor(m, xor (m, n)) = n,

reduc forall m: bitstring, key: bitstring; sdec(key, senc(key, m)) = m.

In order to prove authentication, we define the following four events:

event UserAStarted(bitstring),

event UserAAuthened(bitstring),

event UserBStarted(bitstring),

event UserBAuthened(bitstring).

The process part defines the actions of every participant and models the protocol as their parallel execution. The smart cards in the protocol are quite special: they belong to users but look like separate participants. We define an independent participant called infoProvider which models all smart cards as a whole and communicates with users through private channels sca and scb. It is defined below.

Let EmiteB =

let eB = h((IDB, k)) in

out (scb, eB),

let EmitfA =

let RA = H((BA, IDA)) in

let fA = h(RA) in

out(sca, fA),

let EmitfB =

let RB = H((BB, IDB)) in

let fB = h(RB) in

out(scb, fB),

let EmitTIDA =

let TIDA = xor(H((BA, IDA)), h((IDA, k))) in

out(sca, TIDA),

let EmitTIDB =

let TIDB = xor(H((BB, IDB)), h((IDB, k))) in

out(scb, TIDB),

let pubKey = out(c, T(x, k)),

let infoProvider = !EmiteA | !EmiteB | !EmitfA | !EmitfB | !EmitTIDA | !EmitTIDB | !pubKey.

According to the protocol, the core message sequence for the proposed protocol can be described below:

Message 1: User  A → User B: {Ta(x), CA},

Message 2: User  B → Server: {m1, Tb(x), CB},

Message 3: Server → User B: {C3, C4},

Message 4: User  B → User  A: {HBA, C4},

Message 5: User  A → User B: m5 = h(SK| | A| | B).

Actions of User  A include computing and then sending message 1 to User  B, waiting until he receives message 4 from User  B, and then computing and sending message 5 to User  B. Its smart card data are achieved through communicating with the infoProvider. We defined User  A as follows:

let UserA =

event UserAStarted(IDA);   (* step 1* )

let RA = H((BA, IDA)) in

in(sca, xfA: bitstring);

if xfA = h(RA) then

new a: bitstring;

in(sca, xTIDA: bitstring);

let eA = xor(RA, xTIDA) in

let KAS = T(T(x, k), a) in

let HA = h((T(x, a), IDA, IDB, eA)) in

let CA = senc(KAS, (IDA, IDB, HA, T(x, a))) in

out(c, (T(x, a), CA));

in(c, (xHBA: bitstring, xC4: bitstring));   (* step 5* )

let (xIDA: bitstring, xIDB: bitstring, xTbx: bitstring, xHSA: bitstring)

= sdec(KAS, xC4) in

let HSA′ = h((xTbx, xIDA, xIDB, eA)) in

if xHSA = HSA′ then

let SKAB = T(xTbx, a) in

if xHBA = h((SKAB, xIDB, xIDA, xC4)) then

let m5 = h((SKAB, xIDB, xIDA)) in

out(c, m5);

event UserBAuthened(IDB);

let SK′ = h(SKAB) in 0.

Actions of User  B include receiving message 1 from User  A, computing and sending message 2 to the Server, waiting until receiving message 3 from the Server, then computing and sending message 4 to User  A, and finally receiving message 5 from User  A. We define User B as follows:

let UserB =

in(c, (xTax: bitstring, xCA: bitstring));   (* step 2* )

event UserBStarted(IDB);

let RB = H((BB, IDB)) in

in(scb, xfB: bitstring);

if xfB = h(RB) then

new b: bitstring;

in(scb, xTIDB: bitstring);

let eB = xor(RB, xTIDB) in

let KBS = T(T(x, k), b) in

let HB = h((T(x, b), IDB, eB)) in

let CB = senc(KBS, (IDB, HB, T(x, b))) in

out(c, ((xTax, xCA), T(x, b), CB));

in(c, (xC3: bitstring, xC4: bitstring));   (* step 4* )

let (xIDB: bitstring, xIDA: bitstring, xTax: bitstring, xHSB: bitstring) = sdec(KBS, xC3) in

let HSB′ = h((xTax, xIDB, xIDA, eB)) in

if HSB′ = xHSB then

let SKBA = T(xTax, b) in

let HBA = h((SKBA, xIDB, xIDA, xC4)) in

out(c, (HBA, xC4));

in(c, xm5: bitstring);   (* step 6* )

if xm5 = h((SKBA, IDB, IDA)) then

let SK′ = h(SKBA) in

event UserAAuthened(IDA).

The server simply receives message 2 from User  B, computes message 3 and then sends it back to User  B. We defined the server as follows:

let Server =

in(c, (xTaxFromm1: bitstring, xCA: bitstring, xTbxFromm2: bitstring, xCB: bitstring));

let KSA = T(xTaxFromm1, k) in

let (xIDA: bitstring, xIDBFromCA: bitstring, xHA: bitstring, xTaxFromCA: bitstring)

= sdec(KSA, xCA) in

let KSB = T(xTbxFromm2, k) in

let (xIDBFromCB: bitstring, xHB: bitstring, xTbxFromCB: bitstring) = sdec(KSB, xCB) in

if xTaxFromm1 = xTaxFromCA then

if xTbxFromm2 = xTbxFromCB then

let eA′ = h((xIDA, k)) in

let HA′ = h((xTaxFromm1, xIDA, xIDBFromCA, eA′ )) in

let eB′ = h((xIDBFromCA, k)) in

let HB′ = h((xTbxFromm2, xIDBFromCA, eB′ )) in

if xHA = HA′ then

if xHB = HB′ then

let HSB = h((xTaxFromm1, xIDBFromCA, xIDA, eB′ )) in

let C3 = senc(KSB, (xIDBFromCA, xIDA, xTaxFromm1, HSB)) in

let HSA = h((xTbxFromm2, xIDA, xIDBFromCA, eA′ )) in

let C4 = senc(KSA, (xIDA, xIDBFromCA, xTbxFromm2, HSA)) in

out(c, (C3, C4)).

The protocol is defined as the parallel execution of the three participants where exclamation symbol means several instances of the same participant may run at the same time

process !UserA | !UserB | !Server | infoProvider.

The third part of the formal definition – the security property part – defines queries submitted to the ProVerif tool for verification. ProVerif verifies security properties by checking a certain kind of assertion, which is triggered by the query statements. Session key security is verified by checking the attacker query. The ProVerif code for verifying session key security is given below. In the query, attacker (SKAB) means an attacker who can intercept or compute User  A’ s session key. ProVerif verifies the property by checking its reachability in the formal model.

query attacker(SKAB),

query attacker(SKBA).

The authentication property is verified by checking the events’ correspondence assertions. Events are indicators used specifically for authentication verification and have no side effects on the protocol. In our formal definition, four events are defined above to construct two correspondence relations which correspond to two authentications processes respectively: one for the server to authenticate User  A and the other is for the server to authenticate User  B. The queries are defined below.

query id: bitstring; inj-event(UserAAuthened(id)) ⟹ inj-event(UserAStarted(id)),

query id: bitstring; inj-event(UserBAuthened(id)) ⟹ inj-event(UserBStarted(id)).

Execution of the queries in the latest version 1.88 of ProVerif shows that the two attacker queries are not true and the two correspondence queries are true. The former result means that attackers cannot obtain the session key directly, or have knowledge about how to compute the key, so the session key is safe. The latter result means that the authentication property is satisfied in the proposed protocol.

Anonymity requires a system in which User  B with publicly known identity IDV executes the protocol to be indistinguishable from a system in which it is not present at all. In order to prove the user’ s anonymity, the proposed protocol is required to be the observational equivalence to the augmented protocol defined as follows:

process !UserA | !UserB | !Server | infoProvider| ,

let IDB = IDV in (!UserA| !UserB| !Server| infoProvider).

The observational equivalence can be translated into the following ProVerif biprocess:

process !UserA | !UserB | !Server | infoProvider| ,

new ID: bitstring,

let IDB = choice[ID, IDV] in (!UserA| !UserB| !Server| infoProvider).

The right side of the choice represents a system where the user with public identity IDV can run the protocol. The execution of the above process in the latest version 1.88 of ProVerif shows that anonymity of User  B is satisfied. Anonymity of User  A is proved in the same way.

6.2. Other analyses

In this sub-section, we show that the improved protocol can resist various attacks.

6.2.1. Password guessing attack

In our protocol, since users use the secret key ei = h(IDi | | k) instead of passwords to authenticate each other with the help of the trusted server, therefore, it can resist the password guessing attack, and the server does not need to maintain the password table, which has the same advantages as Lee et al.’ s protocol.

6.2.2. Perfect forward secrecy

In our scheme, the session key SK′ = h(TaTb(x)) is related to nonces a and b, which are chosen by Users  A and B respectively and are different in each session run. Hence, even if an adversary can know the server secret key k, he still cannot compute the previously established session keys because of the intractability of the chaotic-maps-based Diffie– Hellman (CM– DH) problem.

6.2.3. Known-key security

Since the session key SK′ = h(TaTb(x)) is dependent on the random nonces a and b, these two nonces are different in all sessions. Therefore, an adversary cannot compute the previous nor the future session keys when he knows one session key.

6.2.4. Forgery and impersonation attacks

Since user i’ s secret key ei = h(IDi | | k) is protected by his personal biometrics Bi, therefore, even if an adversary can know all the information stored in user i’ s smart card, he still cannot extract the correct secret key ei = h(IDi | | k) from TIDi = Ri⊕ ei = H(Bi | | IDi)⊕ h(IDi | | k) without knowing Bi. Thus, the forged message mi = {Ta(x), Ci} cannot pass through the authentication process of the server S, so this attack cannot succeed.

6.2.5. Replay attack

If an adversary impersonates A (or B) and replays A’ s (or B’ s) message to S, and though the replayed message can pass through the authentication process of the server S, the adversary cannot extract the correct information from received message generated by S, and cannot compute the session key due to CM– DH problem either.

6.2.6. Man-in-the-middle attack

In our protocol, the server authenticates users via the shared secret keys ei = h(IDi | | k), which are protected by personal biometrics Bi of users, so an adversary is unable to succeed in impersonating and replaying according to the above analysis. Therefore, man-in-the-middle attack cannot succeed.

6.2.7. User anonymity

In our protocol, all transmitted messages are related to random nonces a and b, which are chosen by Users  A and B respectively, and are different in all sessions. Therefore, an adversary cannot extract nor verify the identities of users according to the communication messages.

7. Performance comparison

Since Lee et al.’ s protocol is a first chaotic-maps-based three-party-authenticated key exchange scheme without using passwords, in this section, we only compare our protocol with Lee et al.’ s protocol in terms of computation cost.

Let C, h, H, and E be the time for performing a Chebyshev polynomial computation, a one-way hash function, a biohashing operation and a symmetric encryption/decryption operation, respectively. Table  1 presents the average running times of some commonly used operations estimated by Xue and Hong[14] in 2012, and shows that Chebyshev polynomial computation is slower than hash function and symmetric encryption/decryption operation. We ignore exclusive OR, and string concatenation operations which are negligible compared with other operations. The performance comparison between our scheme and Lee et al.’ s protocol is given in Table  2. From Table  2, we can conclude that Chebyshev polynomial computations of our scheme are less than Lee et al.’ s protocol, but hash function operations are more than Lee et al.’ s protocol, and our protocol needs two additional biohashing operations.

Table 1. Running times of different operations.
Table 2. Performance comparison.
8. Conclusions

In this paper, we show that the first chaotic-maps-based three-party-authenticated key exchange scheme without using passwords, proposed by Lee et al., is vulnerable to impersonation attack. Then, an improved biometrics-based 3AKE protocol without using passwords is proposed. The improved scheme is safe according to formal verification, and the computation is acceptable.

Reference
1 He D J, Chen C, Ma M D, Chan S and Bu J J 2013 Int. J. Commun. Syst. 26 495 DOI:10.1002/dac.1355 [Cited within:1]
2 Khan M K and Kumari S 2014 Secur. Commun. Netw. 7 399 DOI:10.1002/sec.v7.2 [Cited within:1]
3 Mishra D, Das A K and Mukhopadhyay S 2014 Expert Syst. Appl. 41 8129 DOI:10.1016/j.eswa.2014.07.004 [Cited within:1]
4 Xie Q, Tan X, Wong D S, Wang G, Bao M and Dong N 2014 Secur. Commun. Netw. 7 1264 DOI:10.1002/sec.v7.8 [Cited within:1]
5 He D, Chen J and Hu J 2012 J. Int. Technol. 13 405 [Cited within:1]
6 Özkaynak F and Yavuz S 2013 Nonlinear Dyn. 74 551 DOI:10.1007/s11071-013-0987-4 [Cited within:1]
7 Zhang L 2008 Chaos Soliton. Fract. 37 669 DOI:10.1016/j.chaos.2006.09.047 [Cited within:2]
8 Wang X Y and Liu L T 2013 Chin. Phys. B 22 050503 DOI:10.1088/1674-1056/22/5/050503 [Cited within:1]
9 Qi G Y and Sand ra B M 2014 Chin. Phys. B 23 050507 DOI:10.1088/1674-1056/23/5/050507 [Cited within:1]
10 Deng S, Li Y and Xiao D 2010 Commun. Nonlinear Sci. Numer. Simul. 15 1338 DOI:10.1016/j.cnsns.2009.05.065 [Cited within:1]
11 Farash M S and Attari M A 2014 Nonlinear Dyn. 76 1203 DOI:10.1007/s11071-013-1204-1 [Cited within:1]
12 He D, Chen Y and Chen Y 2012 Nonlinear Dyn. 69 1149 DOI:10.1007/s11071-012-0335-0 [Cited within:1]
13 Tan Z 2013 Nonlinear Dyn. 72 311 DOI:10.1007/s11071-012-0715-5 [Cited within:1]
14 Xue K and Hong P 2012 Commun. Nonlinear Sci. Numer. Simulat. 17 2969 DOI:10.1016/j.cnsns.2011.11.025 [Cited within:1]
15 Lin H Y 2015 Commun. Nonlinear Sci. Numer. Simulat. 20 482 DOI:10.1016/j.cnsns.2014.05.027 [Cited within:1]
16 Yoon E and Jeon I 2011 Commun. Nonlinear Sci. Numer. Simulat. 16 2383 DOI:10.1016/j.cnsns.2010.09.021 [Cited within:1]
17 Wang X and Zhao J 2010 Commun. Nonlinear Sci. Numer. Simulat. 15 4052 DOI:10.1016/j.cnsns.2010.02.014 [Cited within:1]
18 Lai H, Xiao J, Li L and Yang Y 2012 Math. Probl. Eng. 2012 454823 DOI:10.1155/2012/454823 [Cited within:2]
19 Zhao F, Gong P, Li S, Li M and Li P 2013 Nonlinear Dyn. 74 419 DOI:10.1007/s11071-013-0979-4 [Cited within:1]
20 Lee C, Li C and Hsu C 2013 Nonlinear Dyn. 73 125 DOI:10.1007/s11071-013-0772-4 [Cited within:1]
21 Hu X X and Zhang Z F 2014 Nonlinear Dyn. 78 1293 DOI:10.1007/s11071-014-1515-x [Cited within:1]
22 Xie Q, Hu B, Dong N and Wong D S 2014 PLoS ONE 9e 102747 DOI:10.1371/journal.pone.0102747 [Cited within:1]
23 Xie Q, Zhao J and Yu X 2013 Nonlinear Dyn. 74 1021 DOI:10.1007/s11071-013-1020-7 [Cited within:1]
24 Lai H, Orgun M A, Xiao J H, Pieprzyk J, Xue L Y and Yang Y X 2014 Nonlinear Dyn. 77 1427 DOI:10.1007/s11071-014-1388-z [Cited within:1]
25 Farash M S and Attari M A 2014 Nonlinear Dyn. 77 399 DOI:10.1007/s11071-014-1304-6 [Cited within:1]
26 Xie Q, Hu B and Wu T 2015 Nonlinear Dyn. 79 2345 DOI:10.1007/s11071-014-1816-0 [Cited within:1]
27 Shu J 2015 Chin. Phys. B 24 060509 DOI:10.1088/1674-1056/24/6/060509 [Cited within:1]
28 Lee C C, Li C T, Chiu S T and Lai Y M 2015 Nonlinear Dyn. 79 2485 DOI:10.1007/s11071-014-1827-x [Cited within:2]
29 Li C T and Hwang M S 2010 J. Netw. Comput. Appl. 33 1 DOI:10.1016/j.jnca.2009.08.001 [Cited within:1]
30 Abadi M, Blanchet B and Lundh H C 200921st International Conference on Computer Aided Verification, June 26, 2009, Grenoble, France, 35 49 DOI:10.1007/978-3-642-02658-4_5 [Cited within:1]
31 Abadi M and Fournet CProceedings of the 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, 2001, New York, USA, 104 [Cited within:1]
32 Dolev D and Yao A C 1983 IEEE Tran. Inform. Theory 29 198 DOI:10.1109/TIT.1983.1056650 [Cited within:1]