†Corresponding author. E-mail: sdnjchq@zjut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61403343 and 61433003), the Scientific Research Foundation of Education Department of Zhejiang Province, China (Grant No. Y201329260), and the Natural Science Foundation of Zhejiang University of Technology, China (Grant No. 1301103053408).
A full-order sliding mode control based on a fuzzy extended state observer is proposed to control the uncertain chaos in the permanent magnet synchronous motor. Through a simple coordinate transformation, the chaotic PMSM model is transformed into the Brunovsky canonical form, which is more suitable for the controller design. Based on the fuzzy control theory, a fuzzy extended state observer is developed to estimate the unknown states and uncertainties, and the restriction that all the system states should be completely measurable is avoided. Thereafter, a full-order sliding mode controller is designed to ensure the convergence of all system states without any chattering problem. Comparative simulations show the effectiveness and superior performance of the proposed control method.
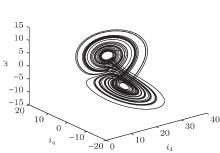
Due to higher efficiency, larger power density, and lower manufacturing cost, permanent magnet synchronous motors (PMSMs) have been widely used in industrial applications. As described in Refs. [1] and [2], the PMSM systems with smooth air gap (Ld = Lq) and non-smooth air gap (Ld ≠ Lq) behave in chaotic manners when system parameters fall into a certain area, respectively. Since the chaotic behavior may destroy the stability of the motor system, how to control and suppress chaos in the PMSM system becomes an important task and many approaches have been proposed in Refs. [3]– [7].
Sliding mode control (SMC) is a kind of robust control technique, and widely used for systems with uncertainties and bounded disturbances. As we know, the existence of a switching function in the controller design will lead to an unavoidable chattering phenomenon in the conventional SMC scheme. Therefore, many efforts have been made for attenuating the chattering problem, and desirable reduced-order dynamics of the system can be obtained by choosing appropriate sliding-mode surfaces.[8– 11] Recently, a full-order sliding mode control scheme was presented in Ref. [12] to make the control signal smooth, and thus the chattering problem is reduced much in the system response. Unfortunately, all the states in the system should be completely known in advance, which may block its applications in the PMSM control system as some system states are unmeasurable.
With the advantages in the nonlinear control system, the observer-based control has been widely used in industrial applications. Compared with most existing observers, the extended state observer (ESO) is able to estimate the system states and model uncertainties simultaneously by viewing them as an extended state. As a model-free control approach, the ESO-based control scheme has been applied to a wide variety of plants.[13– 16] However, the coefficients of ESO usually need to be determined in advance. Recently, fuzzy logic control (FLC) is regarded as one of the most commonly used tools in functional approximation and parameter optimization.[17] In the FLC, a set of linguistic control rules about the concepts of fuzzy implication are given first, and then fuzzy variables are adjusted according to expert knowledge and error. It can provide an effective way for setting and optimizing parameters, which is an important application in practical control engineering. Therefore, the use of fuzzy-based optimization to tune the coefficients of the ESO has the potential ability to improve the control performance.
Motivated by previous work, a full-order sliding mode control based on the fuzzy extended state observer (FSMC+ FESO) is proposed in this paper to control chaos in the permanent magnet synchronous motor (PMSM). An FESO is designed to estimate the unknown states and uncertainties of the chaotic PMSM with ESO coefficients being tuned via fuzzy logic rules, and thus the restriction that all the system states should be completely measurable is avoided. Then, a full-order sliding-mode controller based on the FESO is proposed to control all the chaotic states to zero rapidly and smoothly.
The rest of the paper is organized as follows. Section 2 briefly describes the chaotic permanent magnet synchronous motor system with some transformations. The fuzzy extended state observer and the full-order sliding mode controller design as well as corresponding stability analysis are given in Sections 3 and 4, respectively. Comparative simulations are given in Section 5 and the conclusion is provided in Section 6.
The chaotic PMSM system with smooth air gap described in Ref. [1] is given by
 |
where ĩ d, ĩ q, and 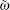
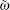
Let 
 |
where xi(i = 1, 2, 3) are state variables, x2 and x3 are unmeasurable; u denotes a control signal; and ũ d = ũ q = T̃ L = 0.
For the convenience of the controller design, the PMSM system (2) is divided into the following two subsystems:
 |
and
 |
It should be noted that the second subsystem (4) can be regarded as an interior dynamic equation of the system (2), which means when x1 and x2 converge to zero, the subsystem (4) becomes ẋ 3 = − x3, which will lead x3 to zero asymptotically. Thus, the control objective is to design the controller u in the subsystem (3) such that the states x1 and x2 can both converge to zero stably.
Define y1 = x1 and y2 = σ (x2 − x1), then the system (3) can be transformed into the following Brunovsky canonical form:
 |
where a(x) and b are unknown function and constant satisfying a(x) = σ [− x2 − x1x3 + γ x1 – σ (x2 − x1)] and b = σ , respectively.
Define b = b0 + Δ b, where b0 is the best available estimate of b, and Δ b is its associated uncertainties. Again, define the uncertainty as a0 = a(x) + Δ bu, which is employed as an extended state y3. Then, the system (5) is rewritten as
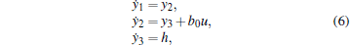 |
where h is the unknown changing rate of the uncertainty a0, i.e., h = ȧ 0.
Let zi(i = 1, 2, 3) be the observing values of the states yi in system (6), and define the observer errors as eoi = yi – zi. Then, the nonlinear extended state observer (NESO) can be expressed as
 |
where β i are the observer gains, while fal(· ) is a nonlinear function in the form
 |
where δ > 0 and 0 < α i < 1.
As pointed out in Refs. [13] and [14], the estimated state variables zi are able to converge to the respective states yi, i.e., zi → yi, by choosing suitable coefficients β i, which can be determined in the following subsection. In other words, the observer errors can converge to satisfy | eoi| = | yi − zi| ≤ di, with di being a small positive constant.
Consider Eq. (7), and we can see that the coefficients β i (i = 1, 2, 3) should be tuned carefully to achieve a good observation performance. In this subsection, the fuzzy logic rules operating on the error variables eo1 and eo2 are utilized to determine the coefficients β i, which can be optimally tuned online according to the fuzzy inputs and the fuzzy logic rules.
The fuzzy input variables are chosen as eo1, eo1, Δ β i, and five linguistic rules (their membership functions) are represented by negative big (NB), negative small (NS), zero, positive small (PS), and positive big (PB), respectively. The fuzzy rules of Δ β i are given in Table 1. Choose a Gaussian function as the membership function of the input eo1 and eo2, and a triangle function as the membership function of the output Δ β i(i = 1, 2, 3). In this paper, the basic universe of eo1 and eo2 are [− 3, + 3] and [− 30, + 30], respectively. The basic universe of Δ β i are [− 0.3, + 0.3], [− 0.1, + 0.1], and [− 0.01, + 0.01], respectively. The fuzzy inference is Mamdani type and the weighted average method is used for the defuzzification.
| Table 1. Fuzzy rules of Δ β i (i = 1, 2, 3). |
According to the membership table, and after fuzzy inference and defuzzification, the coefficients β i can be rectified as
 |
where 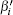
In this section, a full-order sliding mode controller u based on the fuzzy extended state observer (FSMC+ FESO) is designed to suppress the chaotic states x1 and x2 of the subsystem (3).
First of all, a full-order sliding manifold is defined as
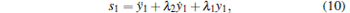 |
where λ 1, λ 2 > 0.
From Eq. (6), equation (10) can be rewritten as
 |
Then, the controller based on the FESO is designed as
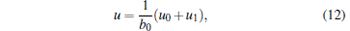 |
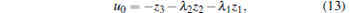 |
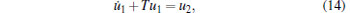 |
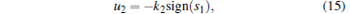 |
where T ≥ 0, k2 = kd + kT + η with η , kd, kT > 0 being control parameters.
Remark 1 The control signal (14) is equivalent to a low-pass filter, where u1 and u2 are the output and input of the filter, respectively. From Eqs. (12)– (15), we can see that through the low-pass filter (14), u1 becomes a smooth signal, and the switching term sign(s1) is not included in the practical control signal u. Therefore, the developed controller is chattering free.
Substituting Eqs. (12)– (15) into Eq. (11), we can obtain
 |
where d(y, z) = (y3 − z3) + λ 2(y2 − z2) + λ 1(y1 − z1) satisfies d(y, z) ≤ ld with ld = l1 + λ 2l2 + λ 1l3.
Differentiate Eq. (17) and we have
 |
In the following, some lemmas and theorems are given to show the stability of the controlled system (6).
Lemma 1[18] Assume that there exists the continuous positive definite function V(t) satisfying the following inequality:
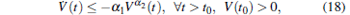 |
where α 1 > 0 and 0 < α 2 < 1 are constants. Then, for any given t0, there exists a finite time ts, and V(t) satisfies the following inequality:
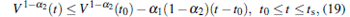 |
and
 |
with ts given by
 |
Theorem 1 Consider the chaotic PMSM system (6), the sliding manifold (10), and control laws (12)– (15). The sliding manifold s1 can converge to zero within a finite time as the control parameters kd and kT satisfy kd ≥ | ḋ (y, z)| and kT ≥ Tld, respectively.
Proof Consider the following Lyapunov function
 |
Differentiating Eq. (22) along with Eqs. (12)– (15), we have
 |
From Eq. (22), we can see that choosing the control parameters kd and kT to satisfy kd ≥ | ḋ (y, z)| and kT ≥ Tld, we can obtain
 |
Then, we have V̇ ≤ − η mV1/2 with η m = η 21/2. According to Lemma 1, it can be concluded that the sliding manifold s1 can converge to zero within a finite time ts given by
 |
Theorem 2 Under the same conditions in Theorem 1, the system states x1, x2, and x3 can asymptotically converge to zero.
Proof When achieving the sliding surface s1 = 0, the states of system (6) will remain on it and the system has the invariant properties. On the sliding surface s1 = 0, we have
 |
with 0 < λ 0 < λ 2 satisfying (λ 2 − λ 0)λ 0 = λ 1.
Define χ = λ 0ẏ 1 + y1, and equation (26) can be rewritten as
 |
Then, it can be directly concluded that χ can converge to zero as time goes to infinity, and thus we have y1 → 0 as t → ∞ . From Eqs. (3) and (4), we can obtain x1, x2 → 0 and ẋ 3 = − x3. As a result, the system states x1, x2, and x3 can converge to zero asymptotically.
Remark 2 Actually, when s1 converges to zero, it is followed by Eqs. (14) and (15) that the controllers u1 and u2 can converge to zero gradually. According to Eq. (16), we can easily conclude that d(y, z) will converge to zero, i.e., eo3 + λ 2eo2 + λ 1eo1 will converge to zero eventually.
In order to show the superior control performance of the proposed scheme, the conventional reduced-order sliding mode control based on fuzzy extended state observer (RSMC+ ESO) in Ref. [7] is performed for comparison. During the following simulations, we consider three different control schemes: (C1) reduced-order sliding mode control with extended state observer (RSMC+ ESO); (C2) full-order sliding mode control with extended state observer (FSMC+ ESO); (C3) proposed full-order sliding mode control with fuzzy extended state observer (FSMC+ FESO). The sliding manifold and controller of C1 scheme are, respectively, designed as
 |
and
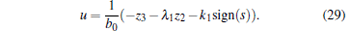 |
For fair comparison, the same initial states and parameters are set, i.e., (x1(0), x2(0), x3(0)) = (− 5, 0.01, 20), λ 1 = 10, λ 2 = 100, b0 = 5, α 1 = 0.5, α 2 = 0.25, α 3 = 0.125, δ = 0.01, and k1 = k2 = 100. In the C1 and C2 schemes, the coefficients of β 1, β 2, and β 3 are set as β 1 = 30, β 2 = 300, β 3 = 1000, respectively; while they are tuned according to the fuzzy logic rules (9) in the C3 scheme.
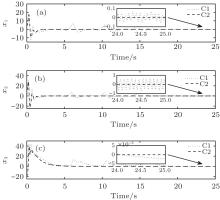
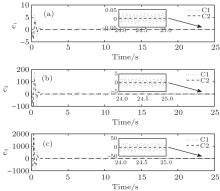
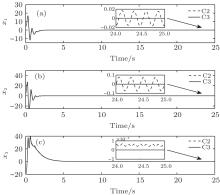
Comparative results are shown in Figs. 2– 7. The control performance, observation errors, and control signals of the C1 scheme (RSMC+ ESO) and C2 scheme (FSMC+ ESO) are depicted in Figs. 2– 4, respectively. From Fig. 2, we can see that compared with the C1 scheme, the C2 scheme has comparatively better control performance with respect to smaller steady-state errors and faster stabilization speed. As shown in Figs. 3 and 4, the C2 scheme has much smaller observation errors than the C1 scheme, and the control signal of the C2 scheme is smoother with much improved chattering phenomenon. Figures 5– 7 provide the comparison performance of the C2 scheme (FSMC+ ESO) and the proposed C3 scheme (FSMC+ FESO). It can be seen that under the effect of fuzzy logic rules, the coefficients of the ESO are optimized and thus the C3 scheme can have a better control performance than the C2 scheme with respect to smaller steady-state errors and observation errors, and much smoother control signal without any chattering problem. The corresponding comparison results can be clearly found in Figs. 5– 7, respectively.
From the discussion and the figures above, we can easily conclude that the proposed FSMC+ FESO scheme can effectively optimize the ESO coefficients and has a better control performance than the other two schemes with respect to smaller steady-state errors, smaller observer errors, and smoother control signals without chattering phenomenon.
In this paper, a full-order sliding mode control based on the fuzzy extended state observer is proposed for suppressing the chaos in the permanent magnet synchronous motor (PMSM) system. The unknown system states and uncertainties are estimated by employing a nonlinear extended state observer, in which the coefficients are tuned by fuzzy logic rules. Then, a full-order sliding mode controller based on the fuzzy extended state observer (FSMC+ FESO) is designed without any chattering problem in control signals. Comparative simulations show the effectiveness and superior control performance of the proposed control method.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|