†Corresponding author. E-mail: fengxq@cust.edu.cn
*Project supported by the Industrial Technology Research and Development Special Project of Jilin Province, China (Grant No. 2013C46) and the Natural Science Foundation of Jilin Province, China (Grant No. 20101510).
A systematic study of the chaotic synchronization of Bose–Einstein condensed body is performed using linear coupling method based on Lyapunov stability theory, Sylvester’s criterion, and Gerschgorin disc theorem. The chaotic synchronization of Bose–Einstein condensed body in moving optical lattices is realized by linear coupling. The relationship between the synchronization time and coupling coefficient is obtained. Both the single-variable coupling and double-variable coupling are effective. The results of numerical calculation prove that the chaotic synchronization of double-variable coupling is faster than that of single-variable coupling and small coupling coefficient can achieve the chaotic synchronization. Weak noise has little influence on synchronization effect, so the linear coupling technology is suitable for the chaotic synchronization of Bose–Einstein condensate.
The Bose– Einstein condensate (BEC) has attracted much attention due to its unique physical properties in fundamental science and technological applications. Recently, BEC has been studied in the field of physics.[1– 7] The quantum behavior and nonlinear characteristics of BEC can be described by using the nonlinear Schrö dinger equation. Very recently, the chaos as a typical nonlinear phenomenon was also found and investigated in the BEC.[8– 10] Two different approximation models were used to study the nonlinear resonance and chaos oscillation in the weak coupling BEC.[11, 12] Coullet and Vandenberghe used a two-modulus model to deduce the condensed matter equation and investigate the chaotic phenomenon of capture effect in the weak irreversible double condensate.[13] Lee et al. studied Melnikov chaos of two-weak coupling condensate.[14] Hai et al. studied the chaos in BEC of moving optical lattices and used the Melnikov method to analyze space– time evolution from stable to unstable chaos.[15] Filho et al. investigated and discussed spatiotemporal chaos in collapse condensate.[16] Later, the chaos control in BEC of moving optical lattices was explored in Refs. [17]– [21]. The above-mentioned studies are mainly concerned with chaotic characteristics and chaos controlling under different conditions.
Since Pecora and Carroll first studied the synchronization of chaotic systems in 1990.[22] Chaos synchronization has been received much attention due to its applications in the secure communications and holographic storage in the past decade. The relationship between absolute stability theory and the synchronization problem was discussed by Curran and Chua.[23] Carroll and Pecora investigated synchronizing non-autonomous chaotic circuits.[24] Kocarev et al.[25] and Bowong et al.[26] applied chaotic synchronization to secure communications, etc. The chaotic synchronization exhibits better security and capability of storage which makes it potentially interesting for industrial applications. The chaotic synchronization has become a widely attractive scientific field.[27– 30] The study of the chaotic dynamics of the BEC system began at 2000 which was regarded as a new research field. Few studies were devoted to the chaotic synchronization in Bose– Einstein condensate (BEC). However, the chaotic synchronization in BEC has a potential application value in quantum communication and information storage. The studies of chaotic synchronization in BEC provide some methods of manipulating and utilizing the BECs. Furthermore, it has a very broad prospect of application in atomic laser, quantum computation, precision measurement, etc. Therefore, it is desirable to investigate the chaotic synchronization in BEC.
In this study, the chaotic synchronization in BEC is investigated systematically. The sufficient conditions of chaotic synchronization in BEC are gained by Lyapunov stability theorem combined with Sylvester’ s criterion and Gerschgorin disc theorem. According to the sufficient conditions of chaotic synchronization in BEC, the chaotic synchronization in BEC is realized by single-variable coupling and double-variable coupling separately. The realization of chaotic synchronization shows that it is easier to realize by using double-variable coupling than by using single-variable coupling. We analyze the influence of the random noise and find that the random noise has little influence on synchronization effect. The synchronization error can be reduced by increasing coupling coefficient.
The linear coupling chaotic synchronization system consists of the master and slave system. The output variables of the master system are coupled to the slave system in a certain proportion. Selecting suitable coupling system to satisfy synchronous conditions, the chaotic master and slave system can achieve precise synchronization. The dynamic equation of the master system can be written as[31, 32]
 |
The corresponding dynamic equation of the slave system is
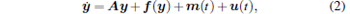 |
where x = (x1, x2, ..., xn)T ∈ Rn and y = (y1, y2, … , yn)T ∈ Rn are the state variables, T denotes transpose of matrix, A ∈ Rn × n is a constant matrix, f is a continuous nonlinear function, m is an external excitation function, u(t) = K(x − y) is the linear coupling term, and K = dia{k1, k2, ..., kn} is a constant coupling matrix. Assume that there exists a bounded matrix M(t) such that
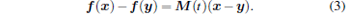 |
The elements of M(t) are dependent on x and y. An error variable of the master and slave system is defined by
 |
then
 |
We select k1, k2, ..., kn such that trajectories of master system x(t) and slave one y(t) satisfy
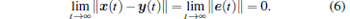 |
The master and slave system can realize the synchronization between them.
According to Lyapunov stability theorem, [33] a sufficient condition that the linear time-varying system (5) is globally asymptotically stable at the origin is that the matrix
 |
is negative definite, where P is a positive definite symmetric constant matrix. For simplicity, we set P = dia{p1, p2, ..., pn}. Rewrite matrix (7) as
 |
and let P(A + M(t)) + (A + M(t))TP = (bij)n× n, bij = bji, i, j = 1, 2, ...n.
By Sylvester’ s criterion and Gerschgorin disc theorem, [34] the symmetric matrix (9) is negative definite if and only if
 |
where
 |
If P = dia{p1, p2, ..., pn} and K = dia{k1, k2, ..., kn} are chosen such that
 |
the master– slave system can achieve chaos synchronization.
As is well known, the mean-field theory is used widely to describe the BECs. In this case, the dynamical equation of the BEC system of moving optical lattices can be given by[35]
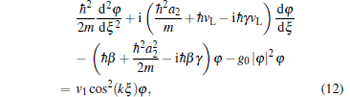 |
where φ represents the wave function of a macroscopic quantum system, vL = δ /2k is the velocity of the optical lattice, ξ = x + vLt is the time and space variable of the system, g0 = 4π ħ 2a/m represents the strength of the atomic interaction with the non-linearity in the GP equation, a is the S-wave scattering length: a > 0 indicates interatomic repulsive interaction and a < 0 indicates interatomic attraction interaction, a2 and β are undetermined constants, and γ denotes the damping coefficient. We use the parameters below and the dimensionless variables to simplify Eq. (12).
Set φ = R(η )eiθ (η ), η = kξ , v = 2mvL/ħ k, β 1 = ħ β /Er,
 |
then the above-mentioned equation will be rewritten as
 |
Let R = y1 and dR/dη = y2, that is to say,
 |
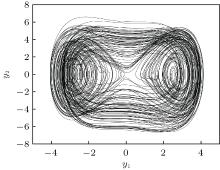
The initial conditions are selected randomly in the attract domain of the chaotic system as y1 (0) = 1.0 and y2 (0) = 0.0. The parameters of the system are v = 2.03, g = − 0.75, γ = 0.05, and I0 = 5.5. As a result, the BEC system of optical lattice becomes chaotic. The chaotic attractor is shown in Fig. 1.
Equation (15) represents the master system, while the slave system after the linear coupling system can be described as
 |
The error between the master and slave system is e = (y1 − y3, y2 − y4)T. The dynamic error can be represented by Eq. (5). According to the above synchronous conditions of the master– slave system, for two chaotic systems (15) and (16), when
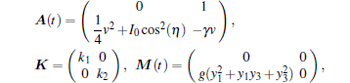
then
 |
Substituting Eq. (17) into (A − K + M(t)) + (A − K + M(t))T yields the following equation:
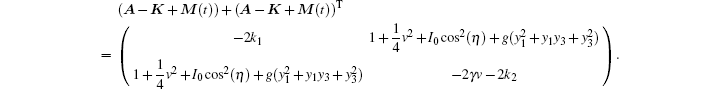
We obtain the synchronous conditions of systems (15) and (16), which must be met for the master– slave system in BECs
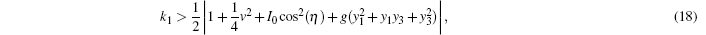 |
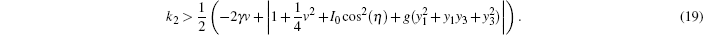 |
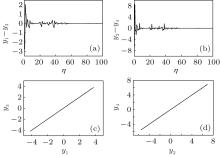
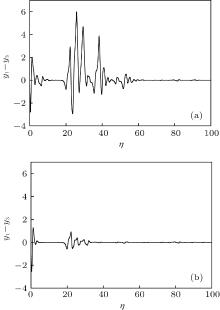
In the case of single-variable linear coupling, we let k2 = 0 and k1 = k. We keep a coupling coefficient. From Fig. 1 it is seen that the bounds of the strange attractor are − 4.2 < y1 < 4.1, − 7.1 < y2 < 6.9. According to the linear coupling chaotic synchronous conditions (18) and (19), we know that the master and slave system can reach synchronization only if k > 1. We choose the initial conditions as y1(0) = 1.0, y2(0) = 0.0, y3(0) = 2.0, and y4(0) = 8.0. When the values of the system parameters are v = 2.03, g = − 0.75, γ = 0.05, and I0 = 5.5, the effects of chaotic synchronization with k = 2.3 are shown in Figs. 2(a) and 2(b). Figures 2(c) and 2(d) show the evolutions of chaotic synchronization on the planes. As shown in the figures, we can see that, although the initial conditions of master– slave system are different, the output errors of the master– slave system are gradually reduced to zero after a transient process. The chaotic synchronization can be realized.
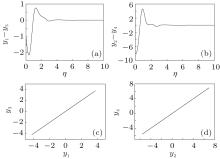 | Fig. 2. Effect diagrams of chaotic synchronization with k = 2.3: (a) y1– y3 versus η and (b) y2– y4 versus η ; the evolutions of chaotic synchronization on plane: (c) y3 versus y1; (d) y4 versus y2. |
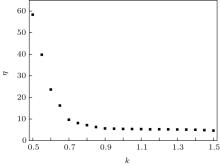
The chaotic system reaches synchronization if the output error of the system is less than 10− 5 and the consumed time is defined as synchronization time. For different coupling coefficients, the system synchronization times are different. With the increase of coupling coefficient, synchronization time decreases. The variation of single-variable linear coupling chaotic synchronization time with coupling coefficient is shown in Fig. 3. It can be seen that the synchronization time is close to the minimum when k = 1.8 and that it does not decrease any more with the increase of the coupling coefficient.
With regard to double-variable linear coupling in the BEC system, we firstly consider the case for k1 = k2 = k. From Fig. 1 we know that the bounds of the strange attractor are − 4.2 < y1 < 4.1, − 7.1 < y2 < 6.9. According to the linear coupling chaotic synchronization criteria (18) and (19), we can realize chaotic synchronization as long as k1 = k2 = k > 0.5. When the initial conditions are also defined as y1 (0) = 1.0, y2 (0) = 0.0, y3 (0) = 2.0, and y4 (0) = 8.0, then we set the values of the parameters as v = 2.03, g = − 0.75, γ = 0.05, and I0 = 5.5. Figures 4(a) and 4(b) show the effects of chaotic synchronization for k1 = k2 = 0.5, while figures 4(c) and 4(d) show the evolutions of chaotic synchronization on the planes. From these figures, we can see that although the initial conditions of master– slave system are different, the output errors of the master– slave system are gradually reduced to zero after a transient process. Chaotic synchronization can be realized.
Double-variable linear coupling is similar to single-variable linear coupling. For different coupling coefficients, the system synchronization time is different. With the increasing of coupling coefficient, the chaos synchronization time decreases. Figure 5 shows the variation of double-linear coupling chaotic synchronization time with the coupling coefficient k. It is found that the synchronization time is close to the minimum at k = 0.9 and does not decrease with the increase of the coupling coefficient.
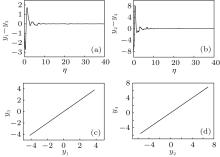
Secondly, we consider the case of k1 ≠ k2. According to the linear coupling chaotic synchronization criteria (18) and (19), the system can realize synchronization at k2 > 0.5 with k1 = 0.5. In this case, we set k1 = 0.5 and change k2 to achieve chaotic synchronization. Figures 6(a) and 6(b) show the effects of chaotic synchronization with k1 = 0.5 and k2 = 0.7, while figures 6(c) and 6(d) show the evolution of chaotic synchronization on the planes. From Figs. 5 and 6 it can be found that the synchronization time for the case of k1 ≠ k2 is shorter than the synchronization time for the case of k1 = k2.
Figure 7 shows the variation of double variable linear coupling chaotic synchronization time with k2 for the case of k1 = 0.5. As shown in the figure, the synchronization time is close to the minimum at k2 = 1.3. No matter how the coupling coefficient k2 increases, the synchronization time does not decrease any more.
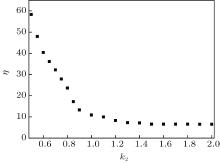 | Fig. 7. Variation of doublevariable linear coupling chaotic synchronization time with k2 for the case of k1 = 0.5. |
In order to check the validity of this method, the random noise δ is added in the synchronization system. Here, we embed the perturbation δ in the slave system as follows:
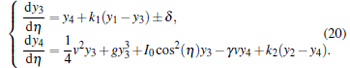 |
The random noise δ is in a range from 0 to 0.06. Figures 8(a) and 8(b) show that the chaotic synchronization can be obtained at δ = 0.05, k = 0.5 and δ = 0.05, k = 0.8 by double-variable linear coupling in the BEC system in the case of k1 = k2 = k. Comparing the two figures, the synchronization error can be reduced by increasing coupling coefficient.
The linear coupling theory is used to derive and calculate the coupling parameter for the chaotic synchronization. The accurate chaotic synchronizations in BEC of moving optical lattices with different initial conditions are realized separately by using single and double variable linear couplings. Numerical analysis indicates that the coupling time decreases with coupling coefficient increasing. We also confirm the presence of the minimum coupling time in chaotic synchronization. Once the minimum coupling time is reached, the coupling time of two systems does not decrease with coupling coefficient increasing. The double-variable coupling synchronization is more effective than single-variable coupling synchronization because single-variable coupling synchronization requires a larger coupling coefficient and a greater coupling synchronization time than double-variable coupling synchronization. In addition, we add the weak noise to slave system and find that the random noise has little influence on synchronization effect. When the strength of the random noise is less than 6%, the chaotic synchronization can also be realized. Furthermore, the synchronization error can be reduced by increasing the value of coupling coefficient. Compared with other linear coupling synchronization, our proposed linear coupling synchronization in the BEC system of moving optical lattices has some advantages, including fast synchronization, a wide range of adaptive parameter, etc. Thus the linear coupling is an effective and suitable method of realizing the chaotic synchronizations in BEC systems of moving optical lattices.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|