Stochastic resonance (SR) has continuously attracted considerable attention from various fields.^{[1– 3]} As an extension of SR, logical stochastic resonance (LSR) refers to the phenomenon that when a nonlinear system is driven by two square waves as inputs, it consistently yields a logical combination of the two input signals in accordance with the truth tables of fundamental logic operations under moderate noise.^[4] The outstanding characteristic of LSR is the capability for the nonlinear logic device to work in an optimal range of environmental noise. As is well known, logical computation devices continue to shrink in size and increase in speed, so it is inevitable that fundamental intrinsic thermal noise which cannot be suppressed or eliminated will be encountered.^[5] Hence, using the interplay between noise and nonlinearity constructively to enhance the reliability of logic operations is a subject of great importance, and LSR presents a practical and reasonable answer for this subject.

LSR has been found to occur in a wide variety of nonlinear systems including electrical systems, ^{[5– 7]} optical systems^{[8, 9]} mechanical, ^[10] chemical^[11] and biological systems.^{[12, 13]} Theoretical studies have been carried out for investigating the effects of different classes of noises like non-Gaussian noise, ^[14] colored noise, ^[15] and 1/f noise^[16] on LSR in nonlinear systems. Besides OR and AND logic operation, XOR logic, which forms the basis of ubiquitous bit-by-bit addition, has also been implemented by manipulating the potential well of the nonlinear system.^[17] During LSR researches, the bistable nonlinear system is a type of widely exploited nonlinear system. The characteristics of LSR in a bistable system with a quartic potential have been investigated by numerical and circuit analog simulations.^{[7, 15, 18– 20]} A kind of parameter-induced LSR in a bistable system has also been proposed to obtain high robust logic operation in a relatively wide range of noise intensity.^[21]

It should be pointed out that during these numerical simulations of LSR in bistable systems, the bit rates of the logical signals are relatively low. The duration of each logic bit lasts from 625  s to 5000  s.^{[4, 7, 15, 16, 18– 22]} While the magnitude of bit rates for practical logical signals could be in kilobits per second (Kbps) or in million bits per second (Mbps). What is the influence of logic bit rate on the performance of LSR in a bistable system? Is the bistable system with fixed parameters suitable for arbitrary high bit rate LSR? Can fast logical computation under moderate noise take advantage of LSR? All of these important points have not been revealed in the literature.

In this paper, we demonstrate that an arbitrary high bit rate LSR can be achieved in a bistable system just by adjusting the parameters of the system and input signals properly. First, we describe the model of LSR in a bistable system and examine the effects of bit rates of logical signals on the performance of LSR while keeping the parameters of the bistable system unchanged. Then, we present a kind of normalized transform of the bistable system and parameter adjusting method to achieve high bit rate LSR. Finally, numerical simulations are carried out to show that the bistable system with quartic potential is suitable for arbitrary high bit rate logic operation, as long as the system parameters and the amplitudes of input noisy logical signals are adjusted according to the normalized transform rule.

Here, a representative nonlinear bistable system with quartic potential function is used to demonstrate the LSR. The nonlinear bistable system is considered as follows:

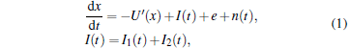where U(x) is the quartic potential function which can be expressed as

The potential function has two potential well minima at and the potential barrier height is Δ U = a²/4b. Thus, parameters a and b control the shape of the potential well and the height of the potential barrier.

In Eq.  (1), I(t) is the input signal which is the sum of two square pulses I₁(t) and I₂(t) encoding the two logic inputs (L₁, L₂) respectively, e is the bias causing asymmetries of the two potential wells, x is the output signal of bistable system, n(t) is an additive zero-mean Gaussian noise with variance 2D, satisfying 〈 n(t)〉 = 0, 〈 n(t)n(0)〉 = 2Dδ (t), where D is the noise strength, δ (t) is the Dirac function. The noise can be denoted as , and ξ (t) is the white noise with zero mean and unit variance.

The logical input– output association is obtained by encoding logic inputs (L₁, L₂) in squares waves I₁(t) and I₂(t). For example, we can set the two inputs I₁(t) and I₂(t) to value − 0.3 when the logic input is 0, and value 0.3 when logic input is 1. The logic inputs being 0 or 1, produce four sets of distinct logic inputs (L₁, L₂): (0, 0), (0, 1), (1, 0), and (1, 1). Since the logic input sets (0, 1) and (1, 0) yield the same I(t) value, the four different input sets can be encoded into three different values of I(t). Thus, the input signal I(t) is a three-level aperiodic wave form. The output x(t) of the bistable system can be decoded into logic output. For a given logic input set (L₁, L₂), a logic output mapping from the output of the nonlinear bistable system can be checked based on the truth table of the basic logic operations shown in Table  1.

Table 1.

Table 1.

Table 1. Relationship between two logic inputs and the logic output of the four fundamental AND, NAND, OR, and NOR gates. Input set (L1, L2) OR NOR AND NAND (0, 0) 0 1 0 1 (0, 1)/(1, 0) 1 0 0 1 (1, 1) 1 0 1 0

Table 1. Relationship between two logic inputs and the logic output of the four fundamental AND, NAND, OR, and NOR gates.

It has been demonstrated that, with an appropriate choice of parameters for the potential energy well and with the noise intensity in a certain range, this bistable system behaves like a robust logic gate. That is, under different sets of logic inputs the system yields correct logic outputs.^{[15, 18, 19]} The type of basic logic operations such as OR, AND, NOR, and NAND are determined by the bias parameter e and the definitions of the system outputs, and it is easy to change from one logic operation to another logic operation flexibly by setting bias parameter e and defining the system outputs appropriately.

However, the bit rates of the logic signals adopted in the above literature for numerical simulation are very slow. The influences of the different bit rates on the performance of LSR exhibited in the bistable system are not studied. In the following, we choose several logic signals with different bit rates and carry out numerical simulation to ascertain whether the nonlinear bistable system with fixed parameters would still yield the desired LSR phenomenon consistently.

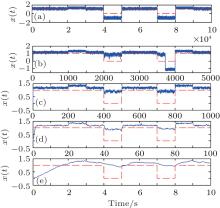
In numerical simulation, equation  (1) is integrated using the Runge– Kutta method. Figure  1 shows the reliable OR operation with logic bit duration T₀ of 1000  s, which denotes relatively slow bit rate of logic input. The I₁(t) and I₂(t) take value − 0.3 when the logic input is 0 and value 0.3 when logic input is 1. The dashed red line on the bottom line indicates the expected OR logic output (with output x > 0 being logic output 1, and x < 0 being logic output 0).

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) and (b) Streams of I1(t) and I2(t), (c) the mixed signal of I(t) and noise with D = 0.18, and (d) output x(t) of the bistable system with a = 1, b = 1, and bias value e = 0.4.

It is observed that the desired OR logic output for slow bit rate logic inputs is obtained. It is due to the cooperation of aperiodic square waves, noise and asymmetry of the potential wells. When we change the bit rates of the logic input signals with keeping the bistable system parameters, bias value, amplitudes of the logical signals, and noise strength unchanged (a = 1, b = 1, e = 0.4, D = 0.18). The output responses of the bistable system described by Eq.  (1) under different bit rate logic input signals are displayed in Fig.  2.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Values of output x(t) under different bit rates of logic input signals. The durations of each bit denoted as T0 for the input logic signals are respectively (a) T0 = 104  s, (b) T0 = 500  s, (c) T0 = 100  s, (d) T0 = 10  s, and (e) T0 = 1  s.

In Fig.  2(a), when the logic bit rate decreases and the corresponding bit duration increases to 10⁴  s, the desired OR logic gate output can still be obtained. When the logic bit rate increases gradually, the response of the bistable system deviates from the desired output more and more severely as shown in Figs.  2(b)– 2(e), and it is impossible to recover the desired OR logic output from the response of the bistable system. This means that a bistable system with small fixed parameters like a = 1, b = 1 is not suitable to achieving the LSR for high bit rate logic input signals even if the bit duration is only 10  s.

Therefore, a further research is needed to ascertain the possibility of achieving the high bit rate LSR in a bistable system by adjusting the parameters. After analyzing the characteristics of the bistable system described by Eq.  (1), we find a method to solve the problem, and the research is based on the normalized transform of the bistable system.

The normalized transform of a bistable system is related to SR with large parameters, which we have proposed in the analysis of stochastic resonance of periodic signal with large parameters.^[23] Fortunately, it is found that the normalized transform of a bistable system can be applied to LSR with high bit rate logic input signals if we take account of the bias value of the bistable system. Equation  (1) can be normalized by making variable changes as follows:

Substituting Eq.  (3) into Eq.  (1) yields

where n(τ /a) is a times stretch of n(τ ) in time domain, which is equivalent to a times compression of n(τ ) in frequency domain. Because the power spectrum density of Gaussian white noise holds constant throughout the whole frequency domain, there is 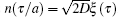, in which ξ (τ ) is zero mean Gaussian white noise with unit variance. Then equation  (4) has a form as follows:

Note that Eqs.  (1) and (5) are equivalent. Equation  (5) is suitable for low bit rate logic input signals to achieve LSR, thus I(τ /a) should be the sum of low bit rate logical signals. When a > 1, the bit rate of I(t) is a times that of I(τ /a). Therefore, to deal with the high bit rate logical signal I(t), a large value of parameter a should be chosen to satisfy that I(τ /a) is within a low bit rate range suitable for LSR, and the amplitudes of I(t), values of bias e and noise should be all magnified 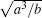times. Substituting their values into Eq.  (5) yields

Hence, if the bistable system described by Eq.  (6) with using I(τ /a), e, and as inputs can achieve LSR, then the bistable system described by Eq.  (1) with using high bit rate logical signals , , and as inputs can also achieve LSR. That means that the high bit rate logical signal shoud be reduced to fold in amplitude and then be stretched 10 times in time domain. Thus it will be transformed into a low bit rate logical signal I(τ /a). This provides an approach to achieving LSR for arbitrary high bit rate logic signals in a bistable system.

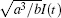
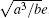
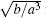
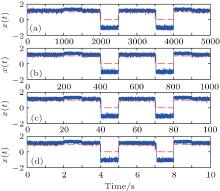
It has been shown that desired OR logic output can be obtained from the response of the bistable system with parameters of a = 1, b = 1, e = 0.4, D = 0.18, and T₀ = 1000  s. When the bit rate of logical inputs increases the desired output cannot be obtained. Now, we carry out numerical simulations by using the same bit rate of logical inputs as shown in Figs.  2(b)– 2(e). By adjusting the system parameters and bias value, amplifying the amplitudes of the logic input signals and noise according to the normalized transform, the responses of a bistable system to different bit rate logic inputs are shown in Fig.  3. The dashed red line in each line has the same meaning as that mentioned above, indicating the expected OR logic output.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Reliable OR logic responses of a bistable system to logical input signals of different bit rates. (a) a = 2, b = 2, e = 0.8, T0 = 500  s, (b) a = 10, b = 10, e = 4, T0 = 100  s, (c) a = 100, b = 100, e = 40, T0 = 10  s, and (d) a = 103, b = 103, e = 400, T0 = 1  s. The amplification factors for logic signals and noise are (a) 2, (b) 10, (c) 100, (d) 103.

Obviously, it is observed that each response of the bistable system is in accordance with the dashed red line. Hence, by choosing appropriate parameters of a bistable system, setting the bias value and amplifying the amplitudes of input logical signals and noise, the desired OR logic output can still be obtained for different bit rate logical inputs. Because there are only bit rate differences among all these logical inputs, if the parameters employed in Figs.  3(a)– 3(d) are normalized, they will deduce to the same set of parameters as a = 1, b = 1, e = 0.4, D = 0.18, T₀ = 1000  s.

During the above numerical simulations, the parameter b is set to be the same value as parameter a, actually, this is not the necessary condition. The value of a must be chosen according to the bit rates of logical input signals based on the normalized transform. While the value of parameter b only affects the selection of bias e and the amplitude amplification factors for logical inputs and noise. Hence, the choice of parameter b can be arbitrary only if the value of bias e and the proper amplification factors for logical inputs and noise are properly set. The responses of a bistable system to logical inputs of bit duration T₀ = 10  s with parameter a = 100 and different values of parameter b are shown in Fig.  4.

It should be pointed out that in Fig.  4(a), the amplitude of expected OR logic output is amplified by a factor of 10 and in Fig.  4(d) by a factor of 0.1 for the purpose of clear comparison with the response of the bistable system. It is clear that the desired OR logic output can be obtained from the responses of the bistable systems with different values of parameter b even though the amplitudes of the system responses vary largely from one to another. The value of bias e and the amplification factors for logical inputs and noise are adjusted according to the principle of the normalized transform. All these parameters will be deduced to the same set of parameters as a = 1, b = 1, e = 0.4, D = 0.18, T₀ = 1000  s after the normalization transform.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The reliable OR logic responses of bistable systems with a = 100 and different values of b to logical input with the same bit duration T0 = 10  s. From top to bottom, (a) b = 1, e = 400, (b) b = 100, e = 40, (c) b = 103, e = 12.649, and (d) b = 104, e = 4. The amplification factors for logical input signals and noise are (a) 103, (b) 100, (c) 31.623, (d) 10.

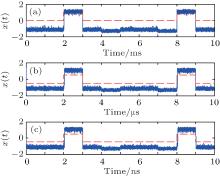
In previous simulations, OR logic operation was mainly simulated in a bistable system described by Eq.  (1) and the value of bias e was positive. It is known that by changing the bias, switching to another logic gate is possible in LSR. In the following, it will be shown that no matter how fast the logical signals vary, the output OR logic gate can be easily changed into AND logic gate by changing the sign of bias e. The results are illustrated in Fig.  5. The dashed red line in each line indicates the expected AND logic output.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. The reliable AND logic responses of bistable systems to logical inputs of different bit rates. The system parameters and bit rates are (a) a = 106, b = 106, e = − 4× 105, 1  kbps, (b) a = 109, b = 109, e = − 4× 108, 1  Mbps, (c) a = 1012, b = 1012, e = − 4× 1011, 1  Gbps. The amplification factors for logical input signals and noise are (a) 106, (b) 109, (c) 1012.

It can be seen from Fig.  5 that reliable AND logic outputs are obtained with negative bias values. The system parameters and the mixed signal of logical input signal and noise amplification factors are determined according to the normalized transform. It is shown that as the bit rates of the logical signals vary from 1  kbps to 1  Gbps, the value of parameter a varies from 10⁶ to 10⁹. The other two complementary logic gates, NOR and NAND, can be obtained by inversing the output interpretation of OR and AND logic gates. In fact, the parameter a is of great importance in high bit rate LSR. Namely, the choice of parameter a should satisfy the condition: the bit rate after the normalized transform is within a low bit rate range. This can be interpreted by the Kramers rate of a bistable system. Equation  (1) describes a particle motion in the asymmetric double potential well. According to the theory of adiabatic approximation, ^[24] when the bistable system is only subjected to noise force driving, the particle will hop between two potential wells at the Kramers rate r_k given by

The value of r_k depends on system parameters and noise strength. The upper limit of Eq.  (7) is 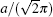as the noise strength D approaches to infinity. To achieve LSR, the bit rate of logical signals should be under the upper limit. When parameter a takes a value of 1, the upper limit is far less than 1, which determines that the input logical signals should be low bit rate ones.

In this paper, the LSR in a nonlinear bistable system to high bit rate logic input signals are investigated. A parameters adjusting method based on normalized transform of a bistable system is put forward to obtain the desired logic output with high bit rate logic inputs. It is shown that the nonlinear bistable system can be used to achieve LSR with high bit rate logic inputs in the presence of moderate noise. Furthermore, the logic response of the system can be easily switched from one logic gate to another by changing the sign of the bias value of the bistable system. It is also validated that there is no logic bit rate limitation with using the bistable system to achieve LSR. Thus the fast and reliable computing device design in engineering can take advantage of LSR exhibited in a nonlinear bistable system with quartic potential function.