Cite this Article
Ma Song-Ya, Gao Cong, Luo Ming-Xing. Efficient schemes of joint remote preparation with a passive receiver via EPR pairs* . Chinese Physics B, 24(11): 110308  
Permissions
Efficient schemes of joint remote preparation with a passive receiver via EPR pairs*
Ma Song-Yaa), Gao Conga), Luo Ming-Xingb)
School of Mathematics and Statistics, Henan University, Kaifeng 475004, China
Information Security and National Computing Grid Laboratory, Southwest Jiaotong University, Chengdu 610031, China

†Corresponding author. E-mail: masongya0829@126.com

*Project supported by the National Natural Science Foundation of China (Grant Nos. 61201253, 61303039, 61572246, and 61502147) and the Fundamental Research Fund for the Central Universities of China (Grant No. 2682014CX095).

Abstract

Novel schemes are put forward to execute the joint remote preparation of an arbitrary two-qubit state with a passive receiver via EPR pairs as the entangled channel. Compared with the previous protocols, the required multi-particle measurement is simplified and the classical communication cost is reduced. When the number of senders increases, the advantage is more evident. It means that the proposed schemes are more efficient in practice.

Keyword: 03.67.Hk; 03.67.–a; 03.65.–w; joint remote preparation; EPR pair; measurement basis; quantum network communication
1. Introduction

The transmission of a quantum state is a primarily important task in quantum information processing. However, the state itself should not be directly sent because any enemy can easily replace it by a fake one without recognition of the authorized parties. The first intriguing protocol for such kind of task is quantum teleportation (QT) which can transmit an unknown qubit between spatially separated parties by utilizing a prior shared entanglement and some classical communication.[1] The QT demonstrates the interchangeability of different types of resources and has made considerable progress.[2– 5] In case the sender does not own the particle itself but owns all the classical information of the state to be prepared for the remote receiver, Lo proposed another intriguing method called remote state preparation (RSP) to transmit a pure known quantum state.[6] It has been shown that for some special ensembles of states, RSP protocols are more economical than QT due to the sender’ s prior knowledge of the original state.[7] Bennett et al. studied the trade-off between the classical communication cost (CCC) and the required entanglement in RSP distinctly.[8] So far, various theoretical protocols for the generalization of RSP have been addressed, [9– 16] such as RSP via noisy channel, the low-entanglement RSP, the optimal RSP, RSP of the continuous variable, RSP of mixed states, and so on. Some RSP schemes have been experimentally implemented by using linear optical elements and nuclear magnetic resonance technology.[17, 18]

Compared with the traditional RSP with two parties, the multi-party RSP plays an important role in the general quantum network communication and quantum distributed computation. One type of these multi-party RSP schemes is the controlled RSP, in which the controlling party (similar to the trusted center in classical secure protocols) determines whether the quantum information is constructed for the receiver or not. Moreover, the controlling party has no classical information of the quantum state during the preparation procedure. The other is named as joint remote state preparation (JRSP). Different from RSP that all the secret information is provided by one sender, JRSP deals with the situation that the complete classical knowledge of the quantum state is independently shared among numbers of senders who have to cooperatively complete the task. JRSP can be viewed as jointly reconstructing the quantum state (which may be a secret for the receiver) at a remote site, which is somewhat reverse to quantum secret sharing (QSS).[19] In QSS, the secret is divided into several different pieces and then distributed to multiple receivers from one sender. From this point of view, JRSP may be useful for such a secure communication task. Furthermore, in the distributed quantum computation, each party should cooperate with other parties for one quantum task such as Shor’ s algorithm. In this case, JRSP is only one special distributed quantum task.

Since the first appearance of JRSP, [20] various JRSP schemes using different types of quantum entanglement have been presented.[21– 36] Most existing JRSP protocols are probabilistic. Also, a new direction named deterministic JRSP has been put forward to get the unit success probability.[28– 36] Recently, Xia et al. proposed a deterministic JRSP scheme of an arbitrary three-qubit state with a passive receiver.[33] They use the simplest kind of entanglement resource EPR pairs as the quantum channel since the EPR pair can be more easily produced and distributed than the GHZ ones. Moreover, the receiver only needs to apply proper recovery operators at the end instead of carrying out some measurements or controlled-NOT gates and classical communication at the beginning. Following the ideas of Ref.  [33], Chen et al. investigated flexible deterministic JRSP of an arbitrary two-qubit state with a passive receiver.[34] In their protocol with two senders, four EPR pairs are used as the shared quantum resource. The senders Alice and Bob need to perform a four-particle and a two-particle projective measurement, respectively. Moreover, the protocol is extended to the case of M > 2 senders. However, the multi-particle measurement is too large in their protocols, which makes it harder to realize in practice.

In this paper, we re-investigate the JRSP of an arbitrary two-qubit state with a passive receiver under the assumption of using the same entangled resources and preserving the merits in the original schemes.[34] In Section 2, we consider the case of two senders. New sets of measurement basis are constructed which plays a key role in our scheme. It is shown that the state can be prepared with the unit success probability if each sender performs a three-particle projective measurement under the basis and the receiver adopts some appropriate unitary transformations. Comparing with the previous protocol, [34] the proposed one has the following advantages. (i) Our solution balances the workload of the two senders. Each sender needs to carry out a three-particle projective measurement. (ii) Our scheme is more operable. In the previous scheme, one sender needs to perform a four-particle projective measurement. As we know, the realization of a protocol always depends on the most difficult operation and four-particle projective measurement is much harder to realize than three-particle measurement in practice. (iii) The CCC is reduced. These advantages are well reflected even in the situation of M > 2 senders which is discussed in Section 3. While some discussion and conclusions are given in the last section.

2. JRSP scheme with two senders

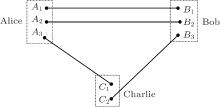
Suppose that two senders Alice and Bob want to help the receiver Charlie remotely prepare an arbitrary two-qubit state

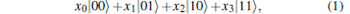where xj, j = 0, … , 3 are complex numbers and satisfy .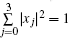

To achieve the JRSP of an arbitrary two-qubit state with complex coefficients xj deterministically, one cannot use the general information splitting method[22] that each sender knows both the partial phase information and amplitude information. The reason is that there does not exist the necessary joint system operations for general complex coefficients. Therefore, similar to previous deterministic JRSP protocols, [28– 36] the classical information {xj = rjeiθ j} of prepared state is split into phase information {rj} and amplitude information {θ j} respectively in this paper. In detail, the state in Eq.  (1) can be rewritten as

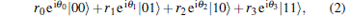where rj eiθ j = xj, real coefficients rj ≥ 0 satisfy the normalization condition , and θ j ∈ [0, 2π ), j = 0, … , 3. It is fully identified by the data set S = {rj, θ j}, which can be split into two subsets S1 = {rj} and S2 = {θ j}. The subset S1 is given to one sender Alice, while the subset S2 is only known to the other sender Bob.

Assume that two senders and the receiver share four EPR pairs

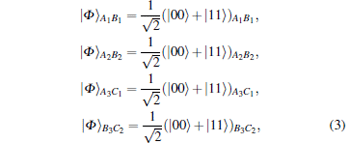as the quantum channel. The particles (A1, A2, A3) belong to the sender Alice, (B1, B2, B3) belong to the sender Bob, while (C1, C2) belong to the receiver Charlie. The distribution of the shared EPR pairs is shown in Fig.  1.

Fig.  1. Quantum channel via four EPR pairs for two senders (Alice, Bob) to jointly prepare a general two-qubit state for the receiver Charlie. In this and all other figures, a qubit is represented by a dot and entangled qubits are connected by solid lines.

Hence, the initial state of the whole system can be written as

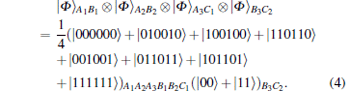In order to realize the JRSP successfully, each sender should measure her (his) qubits under the proper measurement basis that depends on the secret parameters rj, (θ j), j = 0, … , 3 of the prepared state. The construction of the measurement basis are essential to our scheme. Now we demonstrate the process of our scheme as follows.

Step 1 The sender Alice performs a three-particle projective measurement on her particles (A1,   A2,   A3) under the basis {| ζ 0〉 , … , | ζ 7〉 }, which is determined by the subset S1

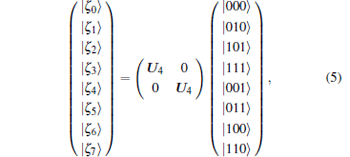where

Obviously, | ζ 0〉 , … , | ζ 7〉 form a complete orthogonal basis in the 8-dimensional Hilbert space as U4 is a unitary matrix. After the measurement, Alice broadcasts the classical message m to Bob and Charlie if the measurement result is | ζ m〉 , m ∈ {0, … , 7}.

After the measurement, the entangled channel in Eq.  (4) can be expanded in terms of the measurement basis | ζ 0〉 , … , | ζ 7〉

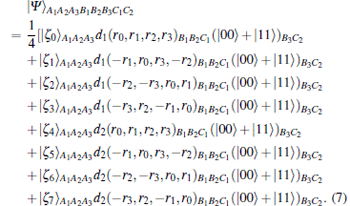Here for convenience, we use the following short notation:

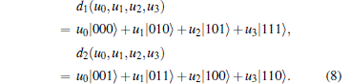Step 2 The sender Bob does not perform the projective measurement immediately but performs a unitary operation Um on his particles (B1, B2, B3) conditioned on the received classical message m, m ∈ {0, … , 7}. Here

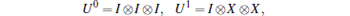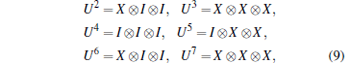
with I being the identity operation, and X being the Pauli operation. Then Bob measures his particles (B1,   B2,   B3) under the complete orthogonal basis {| η 0〉 , … , | η 7〉 } which are determined by the subset S2

where the unitary matrix

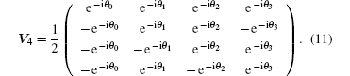In fact, the transition matrix V4 can be rewritten as H D, where

is a 4 × 4 Hadamard matrix and

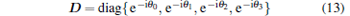is the diagonal matrix of phase factors. Clearly, Bob will obtain a state | η n〉 (n = 0, … , 7) with an equal probability 1/8. He needs also to announce the classical information n to the receiver Charlie.

Step 3 The receiver Charlie performs unitary operations conditioned on the two senders’ measurement results m and n and gets the goal state. Charlie’ s recovery operations are listed in Table  1.

Table 1. The relation among Alice’ s and Bob’ s measurement outcomes (m, n), the collapsed state (CS) of the qubits (C1, C2) after the senders’ measurements, and the receiver Charlie’ s recovery unitary operation (CRUO) on the collapsed state, where m, n ∈ {0, … , 7}.

To see how our protocol works, without loss of generality, assume Alice’ s measurement result is | ζ 1〉 A1A2A3. Then the particles collapse into

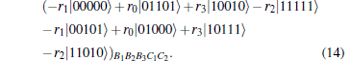In this situation, the sender Bob first performs the unitary operation U1 = I ⊗ X ⊗ X on his particles (B1,   B2,   B3) and obtains

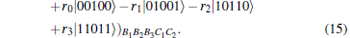
Then Bob performs a three-particle projective measurement on his particles (B1,   B2,   B3) under the basis {| η 0〉 , … , | η 7〉 } defined by Eq.  (10). The state in Eq.  (15) can be rewritten as

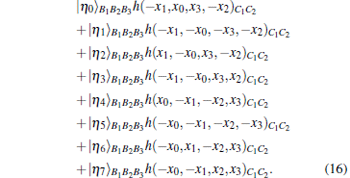where the short notation

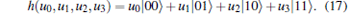From Eq.  (16), one can see whatever Bob’ s measurement outcome is, Charlie can get the prepared state by performing appropriate unitary operation on his collapsed particles. As for the other seven cases corresponding to Alice’ s measurement results, similar analysis process can be made. Here we do not depict them one by one. Charlie’ s recovery unitary operations conditioned on the senders’ measurement results | ζ m〉 A1A2A3, | η n〉 B1B2B3 (m, n = 0, … , 7) are summarized in Table  1.

Therefore, the total success probability for jointly preparing an arbitrary two-qubit state is unit.

3. JRSP scheme with M > 2 senders

The more senders that participate, the higher level of security can be made. In this section, we consider the situation of M > 2 senders. Suppose Alice, Bob, Bob1, … , BobM– 2 are the senders.

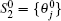
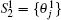
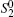
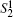
However, the execution with an arbitrary M senders is more complicated. Fortunately, the general outline goes as that of the case of M = 3 senders. Thus, for simplicity we just take M = 3 for an explicit demonstration. In this case, the data subset S2 = {θ j} is divided into two pieces and such that , j = 0, … , 3. is given only to Bob, while is given to Bob1.

The quantum channel is served as six EPR pairs

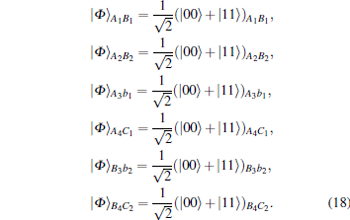As shown in Fig.  2, qubits (A1,   A2,   A3,   A4) belong to the sender Alice, qubits (B1,   B2,   B3,   B4) to the sender Bob, qubits (b1,   b2) to the sender Bob1, and qubits (C1,   C2) to the receiver Charlie.

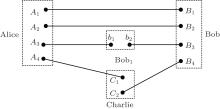Fig.  2. Quantum channel via six EPR pairs for three senders Alice, Bob, Bob1 to jointly prepare a general two-qubit state for the receiver Charlie.

Hence, the initial state of the whole system can be written as

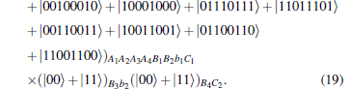The process of our protocol for M = 3 senders is described as follows:

Step 1 The sender Alice performs a four-particle projective measurement on her particles (A1,   A2,   A3,   A4) under the complete orthogonal basis {| ξ 0〉 , … , | ξ 15〉 }, which has the following relationship to the computation basis: {| 0000〉 , … , | 1111〉 }:

where the unitary matrix U4 is defined by Eq.  (6). Alice broadcasts classical information m to Bob and Charlie if the measurement outcome is | ξ m〉 , m ∈ {0, … , 15}.

For simplicity, without loss of generality, we describe the proposal under the assumption that Alice’ s measurement result is | ξ 1〉 A1A2A3A4 in the following.

Step 2 The sender Bob first performs a unitary operation U1 = I ⊗ X ⊗ I ⊗ X on his particles (B1,   B2,   B3,   B4) conditioned on Alice’ s measurement result | ξ 1〉 A1A2A3A4. Then Bob performs a four-particle projective measurement on his particles (B1,   B2,   B3,   B4) under the complete orthogonal basis {| τ 0〉 , … , | τ 15〉 } which are defined by

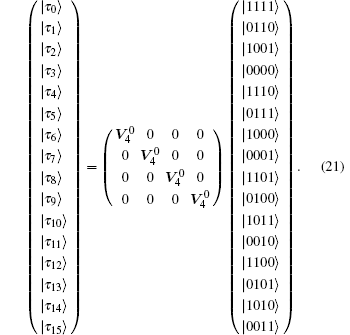Bob broadcasts classical message n to Bob1 and Charlie if his measurement outcome is | τ n〉 , n ∈ {0, … , 15}.

Step 3 Bob1 performs Ib1Xb2 on his particles if Bob’ s measurement result lies in | τ n〉 B1B2B3B4, n ∈ {0, … , 7}. Otherwise, he performs Ib1Ib2. Then Bob1 performs a two-particle projective measurement on his particles (b1, b2) under the complete orthogonal basis {| η 0〉 , … , | η 3〉 } which are defined by

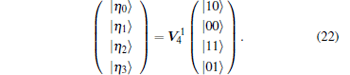Here the transition matrices in Eqs.  (21) and (22) are defined as

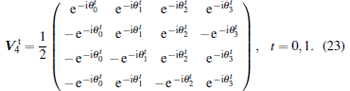After the measurement, Bob1 publishes the classical information n1 to the receiver Charlie if the measurement outcome is | η n1〉 , n1 ∈ {0, … , 3}.

Step 4 Depending on the received classical message n, n1, the receiver Charlie performs the unitary operation shown in Table  2 on his qubits (C1,   C2) to recover the prepared state.

Table 2. Assume Alice’ s measurement outcome is | ξ 1〉 A1A2A3A4. The relation among the Bob and Bob1’ s measurement outcome (n,   n1), the collapsed state (CS) of qubits C1 and C2, and Charlie’ s recovery unitary operation (CRUO) on the collapsed state.

To see how our protocol works, let us express the quantum channel in terms of the measurement basis | ξ 0〉 , … , | ξ 15〉 . The state in Eq.  (19) can be expanded as

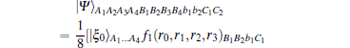
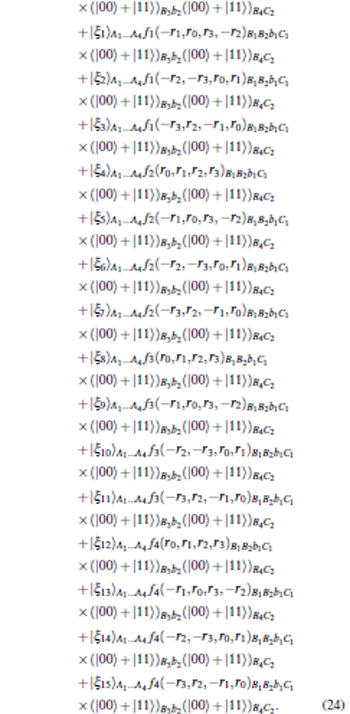Here short notation

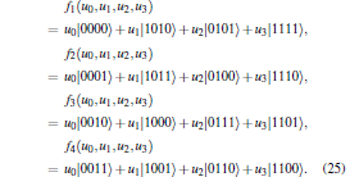If Alice’ s measurement result is | ξ 1〉 A1A2A3A4, the particles collapse into

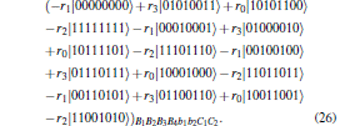In this situation, Bob performs the unitary operation U1 = IB1XB2IB3XB4 and obtains

Then Bob performs a four-particle projective measurement on his particles (B1, … , B4) under the basis {| τ 0〉 , … , | τ 15〉 } defined by Eq.  (21) and broadcasts his measurement result n to Bob1 and Charlie. The state in Eq.  (27) can be rewritten as

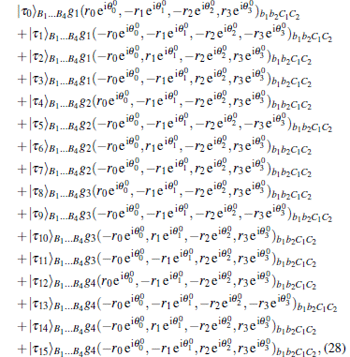where

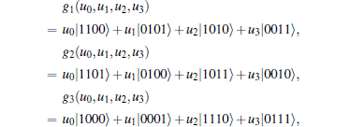
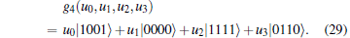For example, if Bob’ s measurement result is | τ 1〉 B1B2B3B4, Bob1 performs Ib1Xb2 on his particles. The collapsed state turns into 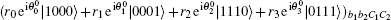, which can be rewritten in terms of the measurement basis | η 0〉 , … , | η 3〉 as

Here h(u0, u1, u2, u3) = u0| 00〉 + u1| 01〉 + u2| 10〉 + u3| 11〉 .

From the above equation, one can see in this situation Charlie can get the prepared state by performing appropriate unitary operations on his collapsed particles. In summary, when Alice’ s measurement result is | ξ 1〉 A1A2A3A4, Charlie’ s recovery unitary operations conditioned on Bob and Bob1’ s measurement results | τ n〉 B1B2B3B4, | η n1〉 b1b2, (n = 0, … , 15, n1 = 0, … , 3) are summarized in Table  2. Similar discussion can be made for other possible measurement outcomes.

Therefore, the receiver Charlie can reestablish the prepared state deterministically.

4. Discussion and conclusions

Considering the protocol for deterministic JRSP of an arbitrary two-qubit with two senders, [34] it uses four EPR pairs as the shared quantum resource. The two senders perform a four-particle and a two-particle projective measurement, respectively. The total CCC is 10  cbits. In fact, the sender Alice needs to broadcast 4  cbits to the sender Bob and the receiver Charlie, and Bob need to send 2  cbits to Charlie. Moreover, this protocol is extended to the general case of M senders.

In this paper, our concern is to realize the deterministic JRSP more efficiently under the promise of using the same entanglement resource. To achieve this target, we make improvements on the existing proposal and present new protocols. It is shown that the proposed protocols are not only easier to be carried out but also spend less CCC. We first investigate the case with two senders. A novel three-particle measurement basis is constructed with the aid of 4 × 4 unitary matrice as the diagonal sub-block of the 8 × 8 transition matrix. It is worth mentioning that construction of the measurement basis plays a key role. In our protocol, three-qubit projective measurement is needed instead of four-qubit measurement. In reality, the difficulty of performing projective measurement increases geometrically as the number of particles increases. In other words, three-particle projective measurement is much easier to be carried out than four-particle measurement, which makes our scheme easier to be realized. As far as the CCC is concerned, the sender Alice broadcasts to Bob and Charlie 3 cubits, and Bob sends Charlie 3 cubits. Thus, 9 cubits are required in the whole process. Moreover, we adopt the strategy that Bob performs unitary operations before performing measurement to avoid choosing different measurement basis depending on Alice’ s measurement result. As for arbitrary M senders, the sender Alice must perform a 2M-particle projective measurement, and other senders perform two-particle projective measurement in the previous scheme. It means that the more senders, the more complicated projective measurements are needed to be carried out by the sender Alice. While in the proposed scheme, it is the most complex to measure (M + 1) particle. It implies that our protocol is more applicable when M becomes larger. In conclusion, we have presented efficient JRSP protocols of an arbitrary two-qubit state by using the same EPR pairs as the quantum channel. Compared with the existing protocol, the most important advantage is that the projective measurement operation is simplified, which means the proposed protocol is more practical.

Reference
1 Bennett C H, Brassard G, Crepeau C, Jozsa R, Peres A and Wootters W K 1993 Phys. Rev. Lett. 70 1895 DOI:10.1103/PhysRevLett.70.1895 [Cited within:1]
2 Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfuter H and Zeilinger A 1997 Nature 575 390 [Cited within:1]
3 Furusawa A 1998 Science 282 706 DOI:10.1126/science.282.5389.706 [Cited within:1]
4 Riebe M, Haffner H, Roos C F, Hansel W, Benhelm J, Lancaster G P T, Korber T W, Becher C, Schmidt-Kaler F, James D F V and Blatt R 2004 Nature 429 734 DOI:10.1038/nature02570 [Cited within:1]
5 Chen X B, Wen Q Y, Xu G, Yang Y X and Zhu F C 2009 Phys. Rev. A 79 036301 DOI:10.1103/PhysRevA.79.036301 [Cited within:1]
6 Lo H K 2000 Phys. Rev. A 62 012313 DOI:10.1103/PhysRevA.62.012313 [Cited within:1]
7 Pati A K 2001 Phys. Rev. A 63 014302 [Cited within:1]
8 Bennett C H, DiVincenzo D P, Shor P W, Smolin J A, Terhal B M and Wootters W K 2001 Phys. Rev. Lett. 87 077902 DOI:10.1103/PhysRevLett.87.077902 [Cited within:1]
9 Xiang G Y, Li J, Yu B and Guo G C 2005 Phys. Rev. A 72 012315 DOI:10.1103/PhysRevA.72.012315 [Cited within:1]
10 Kurucz Z, Adam P, Kis Z and Janszky J 2005 Phys. Rev. A 72 052315 DOI:10.1103/PhysRevA.72.052315 [Cited within:1]
11 Devetak I and Berger T 2001 Phys. Rev. Lett. 87 197901 DOI:10.1103/PhysRevLett.87.197901 [Cited within:1]
12 Berry D W and Sand ers B C 2003 Phys. Rev. Lett. 90 057901 DOI:10.1103/PhysRevLett.90.057901 [Cited within:1]
13 Luo M X, Chen X B, Ma S Y, Yang Y X and Hu Z M 2010 J. Phys. B: At. Mol. Opt. Phys. 43 065501 DOI:10.1088/0953-4075/43/6/065501 [Cited within:1]
14 Ma S Y, Chen X B, Luo M X, Zhang R and Yang Y X 2011 Opt. Commun. 284 4088 DOI:10.1016/j.optcom.2011.04.043 [Cited within:1]
15 Ma S Y, Luo M X, Chen X B and Yang Y X 2014 Quant. Inf. Process. 13 1951 DOI:10.1007/s11128-014-0788-9 [Cited within:1]
16 Ma S Y and Luo M X 2014 Chin. Phys. B 23 090308 DOI:10.1088/1674-1056/23/9/090308 [Cited within:1]
17 Peng X H, Zhu X W, Fang X M, Feng M, Liu M L and Gao K L 2003 Phys. Lett. A 306 271 DOI:10.1016/S0375-9601(02)01604-3 [Cited within:1]
18 Barreiro J T, Wei T C and Kwiat P G 2010 Phys. Rev. Lett. 105 030407 DOI:10.1103/PhysRevLett.105.030407 [Cited within:1]
19 Hillery M, Buzek V and Bertaiume A 1999 Phys. Rev. A 59 1829 DOI:10.1103/PhysRevA.59.1829 [Cited within:1]
20 Xia Y, Song J and Song H S 2007 J. Phys. B: At. Mol. Opt. Phys. 40 3719 DOI:10.1088/0953-4075/40/18/011 [Cited within:1]
21 An N B and Kim J 2008 J. Phys. B: At. Mol. Opt. Phys. 41 095501 DOI:10.1088/0953-4075/41/9/095501 [Cited within:1]
22 Luo M X, Chen X B, Ma S Y, Niu X X and Yang Y X 2010 Opt. Commun. 283 4796 DOI:10.1016/j.optcom.2010.07.043 [Cited within:1]
23 An N B 2010 Opt. Commun. 283 4113 DOI:10.1016/j.optcom.2010.06.016 [Cited within:1]
24 Chen Q Q, Xia Y and An N B 2011 Opt. Commun. 284 2617 DOI:10.1016/j.optcom.2011.01.033 [Cited within:1]
25 Su Y, Chen X B and Yang Y X 2012 Int. J. Quant. Inform. 10 1250006 DOI:10.1142/S021974991100812X [Cited within:1]
26 Zhang Z H, Shu L, Mo Z W, Zheng J, Ma S Y and Luo M X 2014 Quant. Inform. Process. 13 1979 DOI:10.1007/s11128-014-0790-2 [Cited within:1]
27 Choudhury B S and Dhara A 2015 Quant. Inform. Process. 14 373 DOI:10.1007/s11128-014-0835-6 [Cited within:1]
28 An N B 2009 J. Phys. B: At. Mol. Opt. Phys. 42 125501 DOI:10.1088/0953-4075/42/12/125501 [Cited within:2]
29 Xiao X Q, Liu J M and Zeng G H 2011 J. Phys. B: At. Mol. Opt. Phys. 44 075501 DOI:10.1088/0953-4075/44/7/075501 [Cited within:1]
30 An N B, Bich C T and Don N V 2011 Phys. Lett. A 375 3570 DOI:10.1016/j.physleta.2011.08.045 [Cited within:1]
31 Chen Q Q, Xia Y and Song J 2012 J. Phys. A: Math. Theor. 45 055303 DOI:10.1088/1751-8113/45/5/055303 [Cited within:1]
32 Jiang M and Dong D Y 2012 J. Phys. B: At. Mol. Opt. Phys. 45 205506 DOI:10.1088/0953-4075/45/20/205506 [Cited within:1]
33 Xia Y, Chen Q Q and An N B 2012 J. Phys. A: Math. Theor. 45 335306 DOI:10.1088/1751-8113/45/33/335306 [Cited within:2]
34 Chen Q Q, Xia Y and An N B 2013 Phys. Scr. 87 025005 DOI:10.1088/0031-8949/87/02/025005 [Cited within:4]
35 Wang Y and Ji X 2013 Chin. Phys. B 22 020306 DOI:10.1088/1674-1056/22/2/020306 [Cited within:1]
36 Chen Z F, Liu J M and Ma L 2014 Chin. Phys. B 23 020312 DOI:10.1088/1674-1056/23/2/020312 [Cited within:3]